9.1E: Exercises for Section 9.1
( \newcommand{\kernel}{\mathrm{null}\,}\)
In exercises 1 - 4, find the first six terms of each sequence, starting with
1)
- Answer
2)
3)
- Answer
4)
5) Find an explicit formula for
- Answer
6) Find a formula
7) Find a formula
- Answer
8) Find a formula
9) Find a formula
- Answer
10) Find an explicit formula for the
11) Find an explicit formula for the
- Answer
In exercises 12 and 13, find a formula for the general term
12)
13)
- Answer
In exercises 14-18, find a function
14)
15)
- Answer
16)
17)
- Answer
18)
In exercises 19 - 22, plot the first
19) [T]
- Answer
-
Terms oscillate above and below
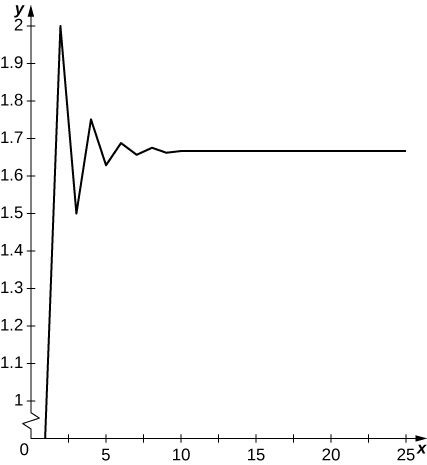
20) [T]
21) [T]
- Answer
-
Terms oscillate above and below
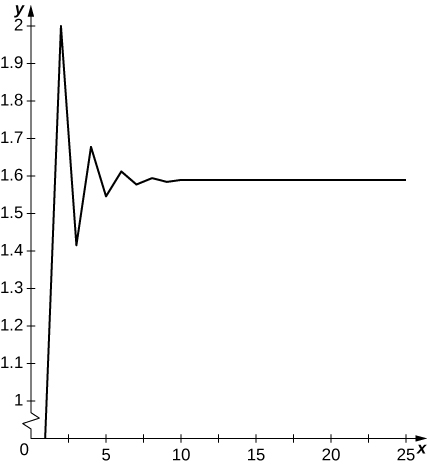
22) [T]
In exercises 23 - 16, suppose that
Using this information, evaluate each of the following limits, state that the limit does not exist, or state that there is not enough information to determine whether the limit exists.
23)
- Answer
24)
25)
- Answer
26)
In exercises 27 - 30, find the limit of each of the following sequences, using L’Hôpital’s rule when appropriate.
27)
- Answer
28)
- Answer
29)
- Answer
30)
In exercises 31 - 37, state whether each sequence is bounded and whether it is eventually monotone increasing or monotone decreasing.
31)
- Answer
- bounded, monotone decreasing for
32)
33)
- Answer
- bounded, not monotone
34)
35)
- Answer
- bounded, decreasing
36)
37)
- Answer
- not monotone, not bounded
In exercises 38 - 39, determine whether the given sequence has a limit. If it does, find the limit.
38)
39)
- Answer
Use the Squeeze Theorem to find the limit of each sequence in exercises 40 - 43.
40)
41)
- Answer
42)
- Answer
43)
- Answer
For the sequences in exercises 44 and 45, plot the first 25 terms of the sequence and state whether the graphical evidence suggests that the sequence converges or diverges.
44) [T]
45) [T]
- Answer
-
Graph oscillates and suggests no limit.
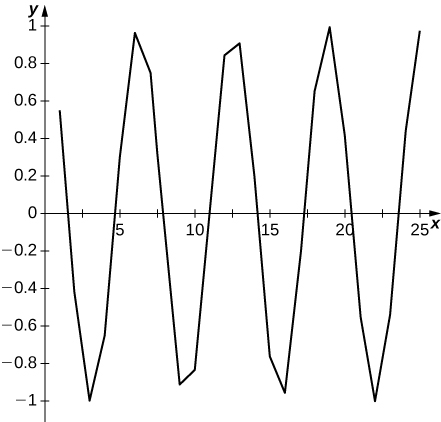
In exercises 46 - 52, determine the limit of the sequence or show that the sequence diverges. If it converges, find its limit.
46)
47)
- Answer
48)
- Answer
49)
- Answer
- Since
50)
51)
- Answer
52)
- Answer
53)
- Answer
Newton’s method seeks to approximate a solution
54) [T]
55) [T]
- Answer
56) [T]
57) [T]
- Answer
58) [T] Suppose you start with one liter of vinegar and repeatedly remove
a. Find a formula for the concentration after
b. After how many steps does the mixture contain less than
- Answer
59) [T] A lake initially contains
a. Explain why the fish population after
b. How many fish will be in the pond after one year?
- Answer
- a. Without losses, the population would obey
b. After
60) [T] A bank account earns
a. Find a recursive formula that gives the amount in the account after
b. How much money will be in the account after
c. Is the amount increasing or decreasing?
d. Suppose that instead of
e. What happens if
- Answer
- a.
c. The amount is decreasing since the withdrawal amount is greater than the interest earned on the principal.
d.
61) [T] A student takes out a college loan of
a. Find a recursive formula that gives the amount left on the loan after
b. If the student makes payments of
c. If the amount left on the loan after
- Answer
- a.
b. The student owes
c. The loan will be paid in full after
62) [T] Consider a series combining geometric growth and arithmetic decrease. Let
63) [T] The binary representation
- Answer
64) [T] To find an approximation for
For the following two exercises, assume that you have access to a computer program or Internet source that can generate a list of zeros and ones of any desired length. Pseudo-random number generators (PRNGs) play an important role in simulating random noise in physical systems by creating sequences of zeros and ones that appear like the result of flipping a coin repeatedly. One of the simplest types of PRNGs recursively defines a random-looking sequence of
65) [T] Starting with
- Answer
- For the starting values
66) [T] Find the first


