8.2E: Fourier Series I (Exercises)

Q8.2.1

1. Prove Theorem 8.1.5.

Q8.2.2

In Exercises 8.2.2-8.2.16 find the Fourier series of $f$ on $[-L,L]$ and determine its sum for $-L\leq x\leq L$. Graph $f$ for Exercises 8.2.2, 8.2.6, 8.2.8, 8.2.15, and 8.2.16 and $$F_{m}(x)=a_{0}+\sum _{n=1}^{m}\left( a_{n}\cos\frac{n\pi x}{L}+b_{n}\sin\frac{n\pi x}{L} \right)\nonumber$$ on the same axes for variable values of $m$.

2. $L=1$; $f(x)=2-x$

3. $L=\pi$; $f(x)=2x-3x^2$

4. $L=1$; $f(x)=1-3x^2$

5. $L=\pi$; $f(x)=|\sin x|$

6. $L=\pi$; $f(x)=x\cos x$

7. $L=\pi$; $f(x)=|x|\cos x$

8. $L=\pi$; $f(x)=x\sin x$

9. $L=\pi$; $f(x)=|x|\sin x$

10. $L=1$; $f(x)= \left\{\begin{array}{cl} 0,&-1<x<-{1\over2},\\ \cos\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.$

11. $L=1$; $f(x)= \left\{\begin{array}{cl} 0,&-1<x<-{1\over2},\\ x\cos\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.$

12. $L=1$; $f(x)= \left\{\begin{array}{cl} 0,&-1<x<-{1\over2},\\ \sin\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.$

13. $L=1$; $f(x)= \left\{\begin{array}{cl} 0,&-1<x<-{1\over2},\\ |\sin\pi x|,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.$

14. $L=1$; $f(x)= \left\{\begin{array}{cl} 0,&-1<x<-{1\over2},\\ x\sin\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.$

15. $L=4$; $f(x)= \left\{\begin{array}{cl} 0,&-4<x<0,\\x,&\phantom{-}0<x<4 \end{array}\right.$

16. $L=1$; $f(x)= \left\{\begin{array}{cl} x^2,&-1< x<0, \\1-x^2,&\phantom{-}0<x<1 \end{array}\right.$

Q8.2.3

17. Verify the Gibbs phenomenon for $f(x)= \left\{\begin{array}{rl} 2,&-2< x< -1,\\1,&-1<x<1,\\-1,&\phantom{-}1< x<2. \end{array}\right.$

18. Verify the Gibbs phenomenon for $f(x)= \left\{\begin{array}{rl} 2,&-3< x< -2,\\3,&-2<x<2,\\1,&\phantom{-}2< x<3. \end{array}\right.$

19. Deduce from Example 11.2.5 that

$$\sum_{n=0}^\infty{1\over(2n+1)^2}={\pi^2\over 8}.\nonumber$$

20.

1. Find the Fourier series of $f(x)=e^x$ on $[-\pi,\pi]$.
2. Deduce from (a) that $$\sum_{n=0}^\infty{1\over n^2+1}={\pi\coth\pi-1\over2}.\nonumber$$

21. Find the Fourier series of $f(x)=(x-\pi)\cos x$ on $[-\pi,\pi]$.

22. Find the Fourier series of $f(x)=(x-\pi)\sin x$ on $[-\pi,\pi]$.

23. Find the Fourier series of $f(x)=\sin kx$ ( $k\ne$ integer) on $[-\pi,\pi]$.

24. Find the Fourier series of $f(x)=\cos kx$ ( $k\ne$ integer) on $[-\pi,\pi]$.

25.

1. Suppose $f(-L)=f(L)$, $f'(-L)=f'(L)$, $f'$ is continuous, and $f''$ is piecewise continuous on $[-L,L]$. Use Theorem 8.2.4 and integration by parts to show that $$f(x)=a_0+\sum_{n=1}^\infty\left(a_n\cos{n\pi x\over L}+b_n\sin{n\pi x\over L}\right),\quad -L\le x\le L,\nonumber$$ with $$a_0={1\over 2L}\int_{-L}^L f(x)\,dx,\nonumber$$ $$a_n= -{L\over n^2\pi^2}\int_{-L}^L f''(x)\cos{n\pi x\over L}\,dx,\quad \text{and} \quad b_n=-{L\over n^2\pi^2}\int_{-L}^L f''(x)\sin{n\pi x\over L}\,dx,\,n\ge1.\nonumber$$
2. Show that if, in addition to the assumptions in (a), $f''$ is continuous and $f'''$ is piecewise continuous on $[-L,L]$, then $$a_n={L^2\over n^3\pi^3}\int_{-L}^Lf'''(x)\sin{n\pi x\over L}\,dx.\nonumber$$

26. Show that if $f$ is integrable on $[-L,L]$ and $$f(x+L)=f(x),\quad -L<x<0\nonumber$$ (Figure 8.2.8), then the Fourier series of $f$ on $[-L,L]$ has the form $$A_0+\sum_{n=1}^\infty\left(A_n\cos{2n\pi\over L}+B_n\sin{2n\pi\over L}\right)\nonumber$$ where $$A_0={1\over L}\int_0^Lf(x)\,dx,\nonumber$$ and $$A_n={2\over L}\int_0^Lf(x)\cos{2n\pi x\over L}\,dx, \quad B_n={2\over L}\int_0^Lf(x)\sin{2n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber$$

Figure 8.2.8: $y=f(x)$, where $f(x+L)=f(x), -L<x<0$

Figure 8.2.9: $y=f(x)$, where $f(x+L)=-f(x), -L<x<0$

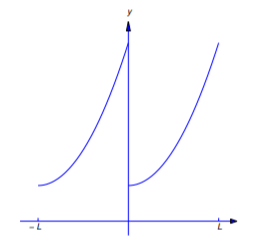
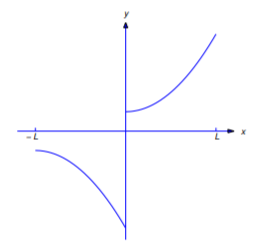
27. Show that if $f$ is integrable on $[-L,L]$ and

$$f(x+L)=-f(x),\quad -L<x<0\nonumber$$

(Figure 8.2.9), then the Fourier series of $f$ on $[-L,L]$ has the form

$$\sum_{n=1}^\infty\left(A_n\cos{(2n-1)\pi x\over L}+B_n\sin{(2n-1)\pi x\over L}\right),\nonumber$$

where

$$A_n={2\over L}\int_0^Lf(x)\cos{(2n-1)\pi x\over L}\,dx \quad \text{and} \quad B_n={2\over L}\int_0^Lf(x)\sin{(2n-1)\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber$$