6.3: Equivalence Relations and Partitions

Recall:

A relation on a set $A$ is an equivalence relation if it is reflexive, symmetric, and transitive. We often use the tilde notation $a\sim b$ to denote a relation.

Also, when we specify just one set, such as  $a\sim b$ is a relation on set $B$, that means the domain & codomain are both set $B$.

For an equivalence relation, due to transitivity and symmetry, all the elements related to a fixed element must be related to each other. Thus, if we know one element in the group, we essentially know all its “relatives.”

Definition: Equivalence Class

Let $R$ be an equivalence relation on set $A$.  For each $a \in A$ we denote the equivalence class of $a$ as $[a]$ defined as:

$$[a]=\{x \in A \mid xRa\}.$$

Example $\PageIndex{1}$

Define a relation $\sim$ on $\mathbb{Z}$ by $$a\sim b \,\Leftrightarrow\, a \mbox{ mod } 4 = b \mbox{ mod } 4.$$  Find the equivalence classes of $\sim$.

Answer

Two integers will be related by $\sim$ if they have the same remainder after dividing by 4.  The possible remainders are 0, 1, 2, 3.

$[0] = \{...,-12,-8,-4,0,4,8,12,...\}$

$[1] = \{...,-11,-7,-3,1,5,9,13,...\}$

$[2] = \{...,-10,-6,-2,2,6,10,14,...\}$

$[3] = \{...,-9,-5,-1,3,7,11,15,...\}$

hands-on exercise $\PageIndex{1}\label{he:relmod6}$

Define a relation $\sim$ on $\mathbb{Z}$ by $$a\sim b \,\Leftrightarrow\, a \mbox{ mod } 3 = b \mbox{ mod } 3.$$  Find the equivalence classes of $\sim$.

example $\PageIndex{2}$

Let $S= \mathscr{P}(\{1,2,3\})=\big \{ \emptyset, \{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\} \big \}.$

For convenience, label

$S_0=\emptyset, \qquad S_1=\{1\}, \qquad S_2=\{2\}, \qquad S_3=\{3\}, \qquad S_4=\{1,2\},\qquad S_5=\{1,3\},\qquad S_6=\{2,3\},\qquad S_7=\{1,2,3\}.$

Define this equivalence relation $\sim$ on $S$ by $$S_i \sim S_j\,\Leftrightarrow\, |S_i|=|S_j|.$$  

Find the equivalence classes of $\sim$.

Answer

Two sets will be related by $\sim$ if they have the same number of elements.  

$[S_0] = \{S_0\}$

$[S_2] =  \{S_1,S_2,S_3\}$

$[S_4] =  \{S_4,S_5,S_6\}$

$[S_7] =  \{S_7\}$

The element in the brackets, [  ]  is called the representative of the equivalence class.  An equivalence class can be represented by any element in that equivalence class. So, in Example 6.3.2, $[S_2] =[S_3]=[S_1]  =\{S_1,S_2,S_3\}.$  This equality of equivalence classes will be formalized in Lemma 6.3.1.

Notice an equivalence class is a set, so a collection of equivalence classes is a collection of sets.

Take a closer look at Example 6.3.1.  All the integers having the same remainder when divided by 4 are related to each other. The equivalence classes are the sets $$\begin{array}{lclcr} {[0]} &=& \{n\in\mathbb{Z} \mid n\bmod 4 = 0 \} &=& 4\mathbb{Z}, \\  {[1]} &=& \{n\in\mathbb{Z} \mid n\bmod 4 = 1 \} &=& 1+4\mathbb{Z}, \\  {[2]} &=& \{n\in\mathbb{Z} \mid n\bmod 4 = 2 \} &=& 2+4\mathbb{Z}, \\  {[3]} &=& \{n\in\mathbb{Z} \mid n\bmod 4 = 3 \} &=& 3+4\mathbb{Z}. \end{array}$$ It is clear that every integer belongs to exactly one of these four sets. Hence, $$\mathbb{Z} = [0] \cup [1] \cup [2] \cup [3].$$ These four sets are pairwise disjoint. From this we see that $\{[0], [1], [2], [3]\}$ is a partition of $\mathbb{Z}$.

Equivalence Classes form a partition (idea of Theorem 6.3.3)

The overall idea in this section is that given an equivalence relation on set $A$, the collection of equivalence classes forms a partition of set $A,$ (Theorem 6.3.3).

The converse is also true: given a partition on set $A$, the relation "induced by the partition" is an equivalence relation (Theorem 6.3.4).

As another illustration of Theorem 6.3.3, look at Example 6.3.2.

$$[S_0] \cup [S_2] \cup [S_4] \cup [S_7]=S$$

$$\big \{[S_0], [S_2], [S_4] , [S_7] \big \} \mbox{ is pairwise disjoint }$$

Thus, $\big \{[S_0], [S_2], [S_4] , [S_7] \big \}$ is a partition of set $S$.

In order to prove Theorem 6.3.3, we will first prove two lemmas.

Lemma $\PageIndex{1}$

If $R$ is an equivalence relation on $A$, then $a R b \rightarrow [a]=[b]$.

Proof

Let $R$ be an equivalence relation on $A$ with $a R b.$
First we will show $[a] \subseteq [b].$
Let $x \in [a], \mbox{ then }xRa$ by definition of equivalence class.  Now we have $x R a\mbox{ and } aRb,$
thus $xRb$ by transitivity (since $R$ is an equivalence relation).  Since $xRb, x \in[b],$ by definition of equivalence classes.
We have shown if $x \in[a] \mbox{ then } x \in [b]$, thus  $[a] \subseteq [b],$ by definition of subset.

Next we will show $[b] \subseteq [a].$
Let $x \in [b], \mbox{ then }xRb$ by definition of equivalence class. Since $a R b$, we also have $b R a,$ by symmetry.
Now we have $x R b\mbox{ and } bRa,$ thus $xRa$ by transitivity. Since $xRa, x \in[a],$ by definition of equivalence classes.
We have shown if $x \in[b] \mbox{ then } x \in [a]$, thus  $[b] \subseteq [a],$ by definition of subset.

$\therefore [a]=[b]$ by the definition of set equality.

One may regard equivalence classes as objects with many aliases. Every element in an equivalence class can serve as its representative. So we have to take extra care when we deal with equivalence classes. Do not be fooled by the representatives, and consider two apparently different equivalence classes to be distinct when in reality they may be identical.

Example $\PageIndex{3}\label{eg:sameLN}$

Define $\sim$ on a set of individuals in a community according to $$a\sim b \,\Leftrightarrow\, \mbox{$a$ and $b$ have the same last name}.$$ We can easily show that $\sim$ is an equivalence relation. Each equivalence class consists of all the individuals with the same last name in the community. Hence, for example, Jacob Smith, Liz Smith, and Keyi Smith all belong to the same equivalence class. Any Smith can serve as its representative, so we can denote it as, for example, $[$Liz Smith$]$.

Example $\PageIndex{4}\label{eg:samedec}$

Define $\sim$ on $\mathbb{R}^+$ according to $$x\sim y \,\Leftrightarrow\, x-y\in\mathbb{Z}.$$ Hence, two positive real numbers are related if and only if they have the same decimal parts. It is easy to verify that $\sim$ is an equivalence relation, and each equivalence class $[x]$ consists of all the positive real numbers having the same decimal parts as $x$ has. Notice that $$\mathbb{R}^+ = \bigcup_{x\in(0,1]} [x],$$ which means that the equivalence classes $[x]$, where $x\in(0,1]$, form a partition of $\mathbb{R}$.

hands-on exercise $\PageIndex{2}\label{he:samedec2}$

Prove that the relation $\sim$ in Example 6.3.4 is indeed an equivalence relation.

Lemma $\PageIndex{2}$

Given an equivalence relation $R$ on set $A$, if $a,b \in A$ then either $[a] \cap [b]= \emptyset$ or $[a]=[b]$

Proof

Let  $R$ be an equivalence relation on set $A$ with $a,b \in A.$

Case 1: $[a] \cap [b]= \emptyset$
In this case $[a] \cap [b]= \emptyset$  or  $[a]=[b]$ is true.

Case 2: $[a] \cap [b] \neq \emptyset$
$\exists x (x \in [a] \wedge x \in [b])$ by definition of empty set & intersection.
$xRa$ and $xRb$ by definition of equivalence classes.  Also since $xRa$, $aRx$ by symmetry.
We have $aRx$ and $xRb$, so $aRb$ by transitivity. Since $aRb$, $[a]=[b]$ by Lemma 6.3.1.
In this case $[a] \cap [b]= \emptyset$  or  $[a]=[b]$ is true.

These are the only possible cases.  So, if $a,b \in A$ then either $[a] \cap [b]= \emptyset$ or $[a]=[b].$
 

Theorem 6.3.3 and Theorem 6.3.4 together are known as the Fundamental Theorem on Equivalence Relations.

Theorem $\PageIndex{3}$

If $R$ is an equivalence relation on any non-empty set $A$, then the distinct set of equivalence classes of $R$ forms a partition of $A$. 

Proof

Suppose $R$ is an equivalence relation on any non-empty set $A$.  Denote the equivalence classes as $A_1, A_2,A_3, ...$.
WMST $A_1 \cup A_2 \cup A_3 \cup ...=A.$
First we will show $A_1 \cup A_2 \cup A_3 \cup ...\subseteq A.$
If $x \in A_1 \cup A_2 \cup A_3 \cup ...,$ then $x$ belongs to at least one equivalence class, $A_i$ by definition of union.
By the definition of equivalence class, $x \in A$.  Thus $A_1 \cup A_2 \cup A_3 \cup ...\subseteq A.$
Next we show $A \subseteq A_1 \cup A_2 \cup A_3 \cup ...$.
If $x \in A$, then $xRx$ since $R$ is reflexive.  Thus $x \in [x]$.
$[x]=A_i,$ for some $i$ since $[x]$ is an equivalence class of $R$.
So, $A \subseteq A_1 \cup A_2 \cup A_3 \cup ...$ by definition of subset.  And so,  $A_1 \cup A_2 \cup A_3 \cup ...=A,$ by the definition of equality of sets.

Now WMST $\{A_1, A_2,A_3, ...\}$ is pairwise disjoint.
For any $i, j$, either $A_i=A_j$ or $A_i \cap A_j = \emptyset$ by Lemma 6.3.2. So, $\{A_1, A_2,A_3, ...\}$ is mutually disjoint by definition of mutually disjoint.

We have demonstrated both conditions for a collection of sets to be a partition and we can conclude 
if $R$ is an equivalence relation on any non-empty set $A$, then the distinct set of equivalence classes of $R$ forms a partition of $A$. 

 Conversely, given a partition $\cal P$, we could define a relation that relates all members in the same component. This relation turns out to be an equivalence relation, with each component forming an equivalence class. This equivalence relation is referred to as the equivalence relation induced by $\cal P$.

Definition

Given $P=\{A_1,A_2,A_3,...\}$ is a partition of set $A$, the relation, $R$,  induced by the partition, $P$, is defined as follows:

$$\mbox{ For all }x,y \in A, xRy \leftrightarrow \exists A_i \in P (x \in A_i \wedge y \in A_i).$$

Example $\PageIndex{5}$

Consider set $S=\{a,b,c,d\}$ with this partition: $\big \{ \{a,b\},\{c\},\{d\} \big\}.$  

Find the ordered pairs for the relation $R$, induced by the partition.

Proof

$R= \{(a,a), (a,b),(b,a),(b,b),(c,c),(d,d)\}$

Theorem $\PageIndex{4}$

If $A$ is a set with partition $P=\{A_1,A_2,A_3,...\}$ and $R$ is a relation induced by partition $P,$ then $R$ is an equivalence relation.

Proof

Let $A$ be a set with partition $P=\{A_1,A_2,A_3,...\}$ and $R$ be a relation induced by partition $P.$  WMST $R$ is an equivalence relation.

Reflexive
Let $x \in A.$ Since the union of the sets in the partition $P=A,$ $x$ must belong to at least one set in $P.$
$\exists i (x \in A_i).$  Since $x \in A_i \wedge x \in A_i,$ $xRx$ by the definition of a relation induced by a partition.
$\therefore R$ is reflexive.

Symmetric
Suppose $xRy.$  $\exists i (x \in A_i \wedge y \in A_i)$ by the definition of a relation induced by a partition.
Since $y \in A_i \wedge x \in A_i, \qquad yRx.$
$\therefore R$ is symmetric.

Transitive
Suppose $xRy \wedge yRz.$ 
$\exists i (x \in A_i \wedge y \in A_i)$ and $\exists j (y \in A_j \wedge z \in A_j)$ by the definition of a relation induced by a partition.
Because the sets in a partition are pairwise disjoint, either $A_i = A_j$ or $A_i \cap A_j = \emptyset.$
Since $y$ belongs to both these sets, $A_i \cap A_j \neq \emptyset,$ thus $A_i = A_j.$ 
Both $x$ and $z$ belong to the same set, so $xRz$ by the definition of a relation induced by a partition. 
$\therefore R$ is transitive.

We have shown $R$ is reflexive, symmetric and transitive, so $R$ is an equivalence relation on set $A.$
$\therefore$ if $A$ is a set with partition $P=\{A_1,A_2,A_3,...\}$ and $R$ is a relation induced by partition $P,$ then $R$ is an equivalence relation.

 

Example $\PageIndex{6}\label{eg:equivrelat-06}$

Over $\mathbb{Z}^*$, define $$R_3 = \{ (m,n) \mid m,n\in\mathbb{Z}^* \mbox{ and } mn > 0\}.$$ It is not difficult to verify that $R_3$ is an equivalence relation. There are only two equivalence classes: $[1]$ and $[-1]$, where $[1]$ contains all the positive integers, and $[-1]$ all the negative integers. It is obvious that $\mathbb{Z}^*=[1]\cup[-1]$.

hands-on exercise $\PageIndex{3}\label{he:equivrelat-03}$

The relation $S$ defined on the set $\{1,2,3,4,5,6\}$ is known to be $$\displaylines{ S = \{ (1,1), (1,4), (2,2), (2,5), (2,6), (3,3), \hskip1in \cr (4,1), (4,4), (5,2), (5,5), (5,6), (6,2), (6,5), (6,6) \}. \cr}$$ Confirm that $S$ is an equivalence relation by studying its ordered pairs. Determine the contents of its equivalence classes.

Example $\PageIndex{7}\label{eg:equivrelat-10}$

Consider the equivalence relation $R$ induced by the partition $${\cal P} = \big\{ \{1\}, \{3\}, \{2,4,5,6\} \big\}$$ of $A=\{1,2,3,4,5,6\}$.

(a) Write the equivalence classes for this equivalence relation.  (b) Write the equivalence relation as a set of ordered pairs. 

Answer

(a) $[1]=\{1\} \qquad [2]=\{2,4,5,6\} \qquad [3]=\{3\}$
 
(b) From the two 1-element equivalence classes $\{1\}$ and $\{3\}$, we find two ordered pairs $(1,1)$ and $(3,3)$ that belong to $R$. From the equivalence class $\{2,4,5,6\}$, any pair of elements produce an ordered pair that belongs to $R$. Therefore, $$\begin{aligned} R &=& \{ (1,1), (3,3), (2,2), (2,4), (2,5), (2,6), (4,2), (4,4), (4,5), (4,6), \\ & & \quad (5,2), (5,4), (5,5), (5,6), (6,2), (6,4), (6,5), (6,6) \}. \end{aligned}$$
 

Summary Review

• A relation $R$ on a set $A$ is an equivalence relation if it is reflexive, symmetric, and transitive.
• If $R$ is an equivalence relation on the set $A$, its equivalence classes form a partition of $A$.
• In each equivalence class, all the elements are related and every element in $A$ belongs to one and only one equivalence class.
• The relation $R$ determines the membership in each equivalence class, and every element in the equivalence class can be used to represent that equivalence class.
• In a sense, if you know one member within an equivalence class, you also know all the other elements in the equivalence class because they are all related according to $R$.
• Conversely, given a partition of $A$, we can use it to define an equivalence relation by declaring two elements to be related if they belong to the same component in the partition.

Exercises 

Exercise $\PageIndex{1}\label{ex:equivrelat-01}$

Find the equivalence classes for each of the following equivalence relations $\sim$ on $\mathbb{Z}$.

a) $m\sim n \,\Leftrightarrow\, |m-3|=|n-3|$

b) $m\sim n \,\Leftrightarrow\, m+n\mbox{ is even }$

Answer

(a) The equivalence classes are of the form $\{3-k,3+k\}$ for some integer $k$. For instance, $[3]=\{3\}$, $[2]=\{2,4\}$, $[1]=\{1,5\}$, and $[-5]=\{-5,11\}$.

(b) There are two equivalence classes: $[0]=\mbox{ the set of even integers }$,  and $[1]=\mbox{ the set of odd integers }$.

Exercise $\PageIndex{2}\label{ex:equivrel-02}$

For this relation $\sim$ on $\mathbb{Z}$ defined by $m\sim n \,\Leftrightarrow\, 3\mid(m+2n)$:

a) show $\sim$ is an equivalence relation.

b) find the equivalence classes for $\sim$.

Exercise $\PageIndex{3}\label{ex:equivrel-03}$

Let $T$ be a fixed subset of a nonempty set $S$. Define the relation $\sim$ on $\mathscr{P}(S)$ by $$X\sim Y \,\Leftrightarrow\, X\cap T = Y\cap T,$$ Show that $\sim$ is an equivalence relation. In particular, let $S=\{1,2,3,4,5\}$ and $T=\{1,3\}$.

a) True or false: $\{1,2,4\}\sim\{1,4,5\}$?

b) How about $\{1,2,4\}\sim\{1,3,4\}$?

c) Find $[\{1,5\}]$

d) Describe $[X]$ for any $X\in\mathscr{P}(S)$.

Answer

(a) True

(b) False

(c) $[\{1,5\}] = \big\{ \{1\}, \{1,2\}, \{1,4\}, \{1,5\}, \{1,2,4\}, \{1,2,5\}, \{1,4,5\}, \{1,2,4,5\} \big\}$

(d) $[X] = \{(X\cap T)\cup Y \mid Y\in\mathscr{P}(\overline{T})\}$. In other words, $S\sim X$ if $S$ contains the same element in $X\cap T$, plus possibly some elements not in $T$.

Exercise $\PageIndex{4}\label{ex:equivrel-04}$

For each of the following relations $\sim$ on $\mathbb{R}\times\mathbb{R}$, determine whether it is an equivalence relation. For those that are, describe geometrically the equivalence class $[(a,b)]$.

1. $(x_1,y_1)\sim(x_2,y_2) \,\Leftrightarrow\, y_1-x_1^2=y_2-x_2^2$.
2. $(x_1,y_1)\sim(x_2,y_2) \,\Leftrightarrow\, (x_1-1)^2+y_1^2=(x_2-1)^2+y_2^2$

Exercise $\PageIndex{5}\label{ex:equivrel-05}$

For each of the following relations $\sim$ on $\mathbb{R}\times\mathbb{R}$, determine whether it is an equivalence relation. For those that are, describe geometrically the equivalence class $[(a,b)]$.

1. $(x_1,y_1)\sim(x_2,y_2) \,\Leftrightarrow\, x_1+y_2=x_2+y_1$
2. $(x_1,y_1)\sim(x_2,y_2) \,\Leftrightarrow\, (x_1-x_2)(y_1-y_2)=0$

Answer

(a) Yes, with $[(a,b)] = \{(x,y) \mid y=x+k \mbox{ for some constant }k\}$. In other words, the equivalence classes are the straight lines of the form $y=x+k$ for some constant $k$.

(b) No. For example, $(2,5)\sim(3,5)$ and $(3,5)\sim(3,7)$, but $(2,5)\not\sim(3,7)$. Hence, the relation $\sim$ is not transitive.

Exercise $\PageIndex{6}\label{ex:equivrel-06}$

For each of the following relations $\sim$ on $\mathbb{R}\times\mathbb{R}$, determine whether it is an equivalence relation. For those that are, describe geometrically the equivalence class $[(a,b)]$.

1. $(x_1,y_1)\sim(x_2,y_2) \,\Leftrightarrow\, |x_1|+|y_1|=|x_2|+|y_2|$
2. $(x_1,y_1)\sim(x_2,y_2) \,\Leftrightarrow\, x_1y_1=x_2y_2$

Exercise $\PageIndex{7}\label{ex:equivrel-07}$

Define the relation $\sim$ on $\mathbb{Q}$ by $$x\sim y \,\Leftrightarrow\, 2(x-y)\in\mathbb{Z}.$$  $\sim$ is an equivalence relation. Describe the equivalence classes $[0]$ and $\big[\frac{1}{4}\big]$.

Answer

We find $[0] = \frac{1}{2}\,\mathbb{Z} = \{\frac{n}{2} \mid n\in\mathbb{Z}\}$, and $[\frac{1}{4}] = \frac{1}{4}+\frac{1}{2}\,\mathbb{Z} = \{\frac{2n+1}{4} \mid n\in\mathbb{Z}\}$.

Exercise $\PageIndex{8}\label{ex:equivrel-08}$

Define the relation $\sim$ on $\mathbb{Q}$ by $$x\sim y \,\Leftrightarrow\, \frac{x-y}{2}\in\mathbb{Z}.$$ Show that $\sim$ is an equivalence relation. Describe the equivalence classes $[0]$, $[1]$ and $\big[\frac{1}{2}\big]$.

Exercise $\PageIndex{9}\label{ex:equivrel-09}$

Consider the following relation on $\{a,b,c,d,e\}$: $$\displaylines{ R = \{(a,a),(a,c),(a,e),(b,b),(b,d),(c,a),(c,c),(c,e), \cr (d,b),(d,d),(e,a),(e,c),(e,e)\}. \hskip0.7in \cr}$$ This is an equivalence relation. Describe its equivalence classes.

Answer

$[a]=\{a,c,e\}$
$[b]=\{b,d\}$

Exercise $\PageIndex{10}\label{ex:equivrel-10}$

Each part below gives a partition of $A=\{a,b,c,d,e,f,g\}$. Find the equivalence relation (as a set of ordered pairs) on $A$ induced by each partition.

(a) $\mathcal{P}_1 = \big\{\{a,b\},\{c,d\},\{e,f\},\{g\}\big\}$

(b) $\mathcal{P}_2 = \big\{\{a,c,e,g\},\{b,d,f\}\big\}$

(c) $\mathcal{P}_3 = \big\{\{a,b,d,e,f\},\{c,g\}\big\}$

(d) $\mathcal{P}_4 = \big\{\{a,b,c,d,e,f,g\}\big\}$

Exercise $\PageIndex{11}\label{ex:equivrel-11}$

Write out the relation, $R$ induced by the partition below on the set $A=\{1,2,3,4,5,6\}.$

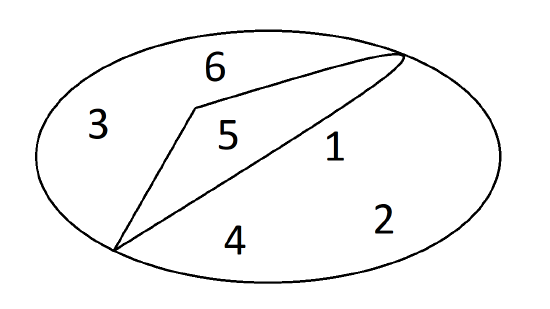
Answer

$R=\{(1,2), (2,1), (1,4), (4,1), (2,4),(4,2),(1,1),(2,2),(4,4),(5,5),(3,6),(6,3),(3,3),(6,6)\}$

Exercise $\PageIndex{12}\label{ex:equivrel-12}$

Consider the relation, $R$ induced by the partition on the set $A=\{1,2,3,4,5,6\}$ shown in exercises 6.3.11 (above).

Answer these questions True or False.

(a) Every element in set $A$ is related to every other element in set $A.$

(b) $(2,3) \in R.$

(c) $(2,1) \in R.$

(d) Every element in set $A$ is related to itself.

(e) The relation, $R$, is transitive.

(f) $5\, R \, 6$

(g) $1\, R\, 4$

(h) $[3]=\{6\}$

(i) $R \subseteq A \times A$

(j) $A \cap R = \emptyset$