8.1: Big O
- Page ID
- 28955
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Big O
The idea of Big O is to characterize functions according to their growth rates. The O refers to the order of a function. In computer science, Big O is used to classify algorithms for their running time or space requirements.
Notice in the figure below that \(f(x)>g(x)\) right before \(x=1\). However, for \(x>1\), we see that \(g(x)>f(x).\) In the long run (namely after \(x>1\)) \(g(x)\) overtakes \(f(x).\)
We say "\(f\) is of order at most \(g\)" or "\(f(x)\) is Big O of \(g(x)\)" .
We write: \(f(x)= O\big(g(x)\big).\)
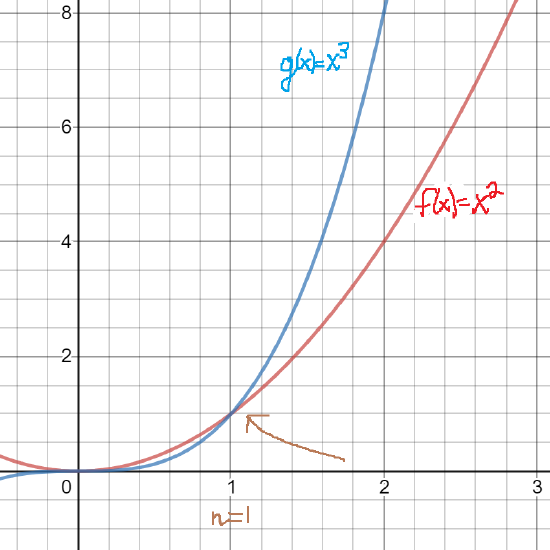
In our definition of Big O notation, there are certain parameters.
- We use \(x\) greater than a certain initial value, \(n\); in the diagram above, \(n=1\).
- We use absolute value for both functions.
- We use \(k\) as a constant multiplied by the function inside the O.
Definition: Big O Notation
\[f(x)= O\big(g(x)\big).\]
if and only if there exist real numbers \(k,n \) with \(k>0 , n\geq 0 \) such that
\[|f(x)| \leq k|g(x)| \qquad \forall x>n.\]
Example \(\PageIndex{1}\)
Take this statement and express it in Big O notation: \(|7x^5+4x^3+x| \leq 14|x^5|\) for \(x>1.\)
- Solution
-
\((7x^5+4x^3+x) \mbox{ is } O(x^5)\)
Comparing orders of common functions
A constant function, such as \(f(x)=6\) does not grow at all. Logarithmic functions grow very slowly. Here is a list of some common functions in increasing order of growth rates.
constant function, logarithmic function, polynomial function, exponential function
Example \(\PageIndex{2}\)
Put these functions in order of increasing growth rates:
\[\log_6x,\qquad x^5,\qquad 2^x,\qquad x^2,\qquad \log_{15}x,\qquad 100x^4,\qquad 64x+1000,\qquad x^5 \log_6x,\qquad 5^x, \qquad 6\]
- Solution
-
\[6, \qquad \log_6x,\qquad \log_{15}x,\qquad 64x+1000,\qquad x^2,\qquad 100x^4,\qquad x^5,\qquad x^5 \log_6x, \qquad 2^x,\qquad 5^x\]
Proofs
We will be using the Triangle Inequality Theorem which is \[|x+y|\ \leq |x|+|y|.\]
Example \(\PageIndex{3}\)
Prove: \(4x^3-11x^2+3x-2=O(x^3)\)
- Proof
-
Choose \(n=1\), i.e. \(x \geq 1.\)
\(|4x^3-11x^2+3x-2 |\leq |4x^3|+|-11x^2|+|3x|+|-2| \qquad \mbox{ by the Triangle Inequality Theorem}\)
\(\qquad \qquad \qquad \qquad \qquad=4x^3+11x^2+3x+2 \qquad \mbox{ applying absolute value; note: }x \mbox{ is positive}\)
\(\qquad \qquad \qquad \qquad \qquad\leq 4x^3+11x^3+3x^3+2x^3 \qquad \mbox{ since }x \mbox{ is positive and greater than 1}\)
\(\qquad \qquad \qquad \qquad \qquad =20x^3\)
\(\qquad \qquad \qquad \qquad \qquad=20|x^3|\qquad \mbox{ since }x \mbox{ is positive and greater than 1}\)
Thus for all \(x \geq 1,\) \(|4x^3-11x^2+3x-2 | \leq 20|x^3|\)
Therefore, using \(n=1\) and \(k=20\), \(4x^3-11x^2+3x-2=O(x^3)\) by the definition of Big O.
Summary and Review
- Big O is used to compare the growth rates of functions.
- Be sure to understand the examples here.
Exercises
exercise \(\PageIndex{1}\)
True or False?
(a) \(11x^3=O(87x^2)\)
(b) \(x^{13}=O(3^x)\)
(c) \(-2x=O(58\log_{35}x)\)
- Answer
-
(a) false
(b) true
(c) false
Exercise \(\PageIndex{2}\)
True or False?
(a) \(4x^3+12x^2+36=O(x^3)\)
(b) \(.01x^5=O(48x^4)\)
(c) \(4^x=O(x^7)\)
(d) \(3x\log_2x=O(25x)\)
Exercise \(\PageIndex{3}\)
True or False?
(a) \(23\ln x=O(3x)\)
(b) \(7x^5=O(x^5)\)
(c) \(x^5=O(7x^5)\)
- Answer
-
all true
Exercise \(\PageIndex{4}\)
Prove: \(2x^5+3x^4-x^3+5x=O(x^5)\)
Example \(\PageIndex{5}\)
Put these functions in order of increasing growth rates:
\[x^7,\qquad 6^x,\qquad 78x^2,\qquad x^2\log x,\qquad 1000x,\qquad 7, \qquad \log_{11}x\]
- Answer
-
\[7, \qquad \log_{11}x, \qquad 1000x, \qquad 78x^2,\qquad x^2\log x, \qquad x^7,\qquad 6^x\]
Exercise \(\PageIndex{6}\)
Take this statement and express it in Big O notation: \(|2x^4-5x^3+x^2-5| \leq 13|x^4|\) for \(x>1.\)


