8.1: Big O

Last updated
Save as PDF

Page ID: 28955

Judy Dean
Monroe Community College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$\newcommand{\longvect}{\overrightarrow}$

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\ket}[1]{\left| #1 \right>}$
$\newcommand{\bra}[1]{\left< #1 \right|}$
$\newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>}$
$\newcommand{\braopket}[3]{\left< #1 \vphantom{#2}\vphantom{#3} \right| #2 \vphantom{#1}\vphantom{#3} \left| #3 \vphantom{#1}\vphantom{#2} \right>}$
$\newcommand{\qmvec}[1]{\mathbf{\vec{#1}}}$
$\newcommand{\op}[1]{\hat{\mathbf{#1}}}$
$\newcommand{\expect}[1]{\langle #1 \rangle}$
$\newcommand{\dfn}[1]{\emph{\textbf{#1}}}$

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Big O

The idea of Big O is to characterize functions according to their growth rates. The O refers to the order of a function. In computer science, Big O is used to classify algorithms for their running time or space requirements.

Notice in the figure below that $f(x)>g(x)$ right before $x=1$. However, for $x>1$, we see that $g(x)>f(x).$ In the long run (namely after $x>1$) $g(x)$ overtakes $f(x).$

We say "$f$ is of order at most $g$" or "$f(x)$ is Big O of $g(x)$" .

We write: $f(x)= O\big(g(x)\big).$

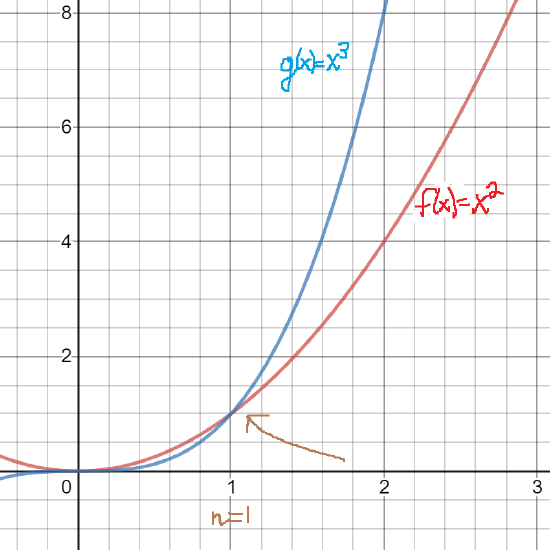
$bigO.png$

In our definition of Big O notation, there are certain parameters.

We use $x$ greater than a certain initial value, $n$; in the diagram above, $n=1$.
We use absolute value for both functions.
We use $k$ as a constant multiplied by the function inside the O.

Definition: Big O Notation

\[f(x)= O\big(g(x)\big).\]

if and only if there exist real numbers $k,n $ with $k>0 , n\geq 0 $ such that

\[|f(x)| \leq k|g(x)| \qquad \forall x>n.\]

Example $\PageIndex{1}$

Take this statement and express it in Big O notation: $|7x^5+4x^3+x| \leq 14|x^5|$ for $x>1.$

Solution: $(7x^5+4x^3+x) \mbox{ is } O(x^5)$

Comparing orders of common functions

A constant function, such as $f(x)=6$ does not grow at all. Logarithmic functions grow very slowly. Here is a list of some common functions in increasing order of growth rates.

constant function, logarithmic function, polynomial function, exponential function

Example $\PageIndex{2}$

Put these functions in order of increasing growth rates:

\[\log_6x,\qquad x^5,\qquad 2^x,\qquad x^2,\qquad \log_{15}x,\qquad 100x^4,\qquad 64x+1000,\qquad x^5 \log_6x,\qquad 5^x, \qquad 6\]

Solution: \[6, \qquad \log_6x,\qquad \log_{15}x,\qquad 64x+1000,\qquad x^2,\qquad 100x^4,\qquad x^5,\qquad x^5 \log_6x, \qquad 2^x,\qquad 5^x\]

Proofs

We will be using the Triangle Inequality Theorem which is \[|x+y|\ \leq |x|+|y|.\]

Example $\PageIndex{3}$

Prove: $4x^3-11x^2+3x-2=O(x^3)$

Proof: Choose $n=1$, i.e. $x \geq 1.$
$|4x^3-11x^2+3x-2 |\leq |4x^3|+|-11x^2|+|3x|+|-2| \qquad \mbox{ by the Triangle Inequality Theorem}$
$\qquad \qquad \qquad \qquad \qquad=4x^3+11x^2+3x+2 \qquad \mbox{    applying absolute value; note: }x \mbox{ is positive}$
$\qquad \qquad \qquad \qquad \qquad\leq 4x^3+11x^3+3x^3+2x^3 \qquad \mbox{    since }x \mbox{ is positive and greater than 1}$
$\qquad \qquad \qquad \qquad \qquad =20x^3$
$\qquad \qquad \qquad \qquad \qquad=20|x^3|\qquad \mbox{         since }x \mbox{ is positive and greater than 1}$

Thus  for all $x \geq 1,$ $|4x^3-11x^2+3x-2 | \leq 20|x^3|$

Therefore, using $n=1$ and $k=20$, $4x^3-11x^2+3x-2=O(x^3)$ by the definition of Big O.

Summary and Review

Big O is used to compare the growth rates of functions.
Be sure to understand the examples here.

Exercises

exercise $\PageIndex{1}$

True or False?

(a) $11x^3=O(87x^2)$

(b) $x^{13}=O(3^x)$

Answer: (a) false
(b) true
(c) false

Exercise $\PageIndex{2}$

True or False?

(a) $4x^3+12x^2+36=O(x^3)$

(b) $.01x^5=O(48x^4)$

(d) $3x\log_2x=O(25x)$

Exercise $\PageIndex{3}$

True or False?

(a) $23\ln x=O(3x)$

(b) $7x^5=O(x^5)$

Answer: all true

Exercise $\PageIndex{4}$

Prove: $2x^5+3x^4-x^3+5x=O(x^5)$

Example $\PageIndex{5}$

Put these functions in order of increasing growth rates:

\[x^7,\qquad 6^x,\qquad 78x^2,\qquad x^2\log x,\qquad 1000x,\qquad 7, \qquad \log_{11}x\]

Answer: \[7, \qquad \log_{11}x, \qquad 1000x, \qquad 78x^2,\qquad x^2\log x, \qquad x^7,\qquad 6^x\]

Exercise $\PageIndex{6}$

Take this statement and express it in Big O notation: $|2x^4-5x^3+x^2-5| \leq 13|x^4|$ for $x>1.$

Search

Text Color

Text Size

Margin Size

Font Type

Definition: Big O Notation