Chapter 1 Review Exercises

Last updated
Save as PDF

Page ID: 30471

Lynn Marecek
Professor (Mathematics) at Santa Ana College
Publisher: OpenStax CNX

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Chapter Review Exercises

Introduction to Whole Numbers

Use Place Value with Whole Number

In the following exercises find the place value of each digit.

Exercise $\PageIndex{1}$

26,915

Answer

tens
ten thousands
hundreds
ones
thousands

Exercise $\PageIndex{2}$

359,417

Exercise $\PageIndex{3}$

58,129,304

Answer

ten millions
tens
hundred thousands
millions
ten thousands

Exercise $\PageIndex{4}$

9,430,286,157

In the following exercises, name each number.

Exercise $\PageIndex{5}$

6,104

Answer: six thousand, one hundred four

Exercise $\PageIndex{6}$

493,068

Exercise $\PageIndex{7}$

3,975,284

Answer: three million, nine hundred seventy-five thousand, two hundred eighty-four

Exercise $\PageIndex{8}$

85,620,435

In the following exercises, write each number as a whole number using digits.

Exercise $\PageIndex{9}$

three hundred fifteen

Answer: 315

Exercise $\PageIndex{10}$

sixty-five thousand, nine hundred twelve

Exercise $\PageIndex{11}$

ninety million, four hundred twenty-five thousand, sixteen

Answer: 90,425,016

Exercise $\PageIndex{12}$

one billion, forty-three million, nine hundred twenty-two thousand, three hundred eleven

In the following exercises, round to the indicated place value.

Exercise $\PageIndex{13}$

Round to the nearest ten.

407
8,564

Answer

410
8,560

Exercise $\PageIndex{14}$

Round to the nearest hundred.

25,846
25,864

In the following exercises, round each number to the nearest 1. hundred 2. thousand 3. ten thousand.

Exercise $\PageIndex{15}$

864,951

Answer

865,000865,000
865,000865,000
860,000

Exercise $\PageIndex{16}$

3,972,849

Identify Multiples and Factors

In the following exercises, use the divisibility tests to determine whether each number is divisible by 2, by 3, by 5, by 6, and by 10.

Exercise $\PageIndex{17}$

168

Answer: by 2,3,6

Exercise $\PageIndex{18}$

264

Exercise $\PageIndex{19}$

375

Answer: by 3,5

Exercise $\PageIndex{20}$

750

Exercise $\PageIndex{21}$

1430

Answer: by 2,5,10

Exercise $\PageIndex{22}$

1080

Find Prime Factorizations and Least Common Multiples

In the following exercises, find the prime factorization.

Exercise $\PageIndex{23}$

420

Answer: 2$\cdot 2 \cdot 3 \cdot 5 \cdot 7$

Exercise $\PageIndex{24}$

115

Exercise $\PageIndex{25}$

225

Answer: 3$\cdot 3 \cdot 5 \cdot 5$

Exercise $\PageIndex{26}$

2475

Exercise $\PageIndex{27}$

1560

Answer: $2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \cdot 13$

Exercise $\PageIndex{28}$

Exercise $\PageIndex{29}$

Answer: $2 \cdot 2 \cdot 2 \cdot 3 \cdot 3$

Exercise $\PageIndex{30}$

168

Exercise $\PageIndex{31}$

252

Answer: $2 \cdot 2 \cdot 3 \cdot 3 \cdot 7$

Exercise $\PageIndex{32}$

391

In the following exercises, find the least common multiple of the following numbers using the multiples method.

Exercise $\PageIndex{33}$

6,15

Answer: 30

Exercise $\PageIndex{34}$

60, 75

In the following exercises, find the least common multiple of the following numbers using the prime factors method.

Exercise $\PageIndex{35}$

24, 30

Answer: 120

Exercise $\PageIndex{36}$

70, 84

Use the Language of Algebra

Use Variables and Algebraic Symbols

In the following exercises, translate the following from algebra to English.

Exercise $\PageIndex{37}$

25−7

Answer: 25 minus 7, the difference of twenty-five and seven

Exercise $\PageIndex{38}$

5$\cdot 6$

Exercise $\PageIndex{39}$

$45 \div 5$

Answer: 45 divided by 5, the quotient of forty-five and five

Exercise $\PageIndex{40}$

x+8

Exercise $\PageIndex{41}$

$42 \geq 27$

Answer: forty-two is greater than or equal to twenty-seven

Exercise $\PageIndex{42}$

3n=24

Exercise $\PageIndex{43}$

$3 \leq 20 \div 4$

Answer: 3 is less than or equal to 20 divided by 4, three is less than or equal to the quotient of twenty and four

Exercise $\PageIndex{44}$

$a \neq 7 \cdot 4$

In the following exercises, determine if each is an expression or an equation.

Exercise $\PageIndex{45}$

$6 \cdot 3+5$

Answer: expression

Exercise $\PageIndex{46}$

y−8=32

Simplify Expressions Using the Order of Operations

In the following exercises, simplify each expression.

Exercise $\PageIndex{47}$

$3^{5}$

Answer: 243

Exercise $\PageIndex{48}$

$10^{8}$

In the following exercises, simplify

Exercise $\PageIndex{49}$

6+10/2+2

Answer: 13

Exercise $\PageIndex{50}$

9+12/3+4

Exercise $\PageIndex{51}$

$20 \div(4+6) \cdot 5$

Answer: 10

Exercise $\PageIndex{52}$

$33 \div(3+8) \cdot 2$

Exercise $\PageIndex{53}$

$4^{2}+5^{2}$

Answer: 41

Exercise $\PageIndex{54}$

$(4+5)^{2}$

Evaluate an Expression

In the following exercises, evaluate the following expressions.

Exercise $\PageIndex{55}$

9x+7 when x=3

Answer: 34

Exercise $\PageIndex{56}$

5x−4 when x=6

Exercise $\PageIndex{57}$

$x^{4}$ when $x=3$

Answer: 81

Exercise $\PageIndex{58}$

$3^{x}$ when $x=3$

Exercise $\PageIndex{59}$

$x^{2}+5 x-8$ when $x=6$

Answer: 58

Exercise $\PageIndex{60}$

$2 x+4 y-5$ when
$x=7, y=8$

Simplify Expressions by Combining Like Terms

In the following exercises, identify the coefficient of each term.

Exercise $\PageIndex{61}$

12n

Answer: 12

Exercise $\PageIndex{62}$

9$x^{2}$

In the following exercises, identify the like terms.

Exercise $\PageIndex{63}$

$3 n, n^{2}, 12,12 p^{2}, 3,3 n^{2}$

Answer: 12 and $3, n^{2}$ and 3$n^{2}$

Exercise $\PageIndex{64}$

$5,18 r^{2}, 9 s, 9 r, 5 r^{2}, 5 s$

In the following exercises, identify the terms in each expression.

Exercise $\PageIndex{65}$

$11 x^{2}+3 x+6$

Answer: $11 x^{2}, 3 x, 6$

Exercise $\PageIndex{66}$

$22 y^{3}+y+15$

In the following exercises, simplify the following expressions by combining like terms.

Exercise $\PageIndex{67}$

17a+9a

Answer: 26a

Exercise $\PageIndex{68}$

18z+9z

Exercise $\PageIndex{69}$

9x+3x+8

Answer: 12x+8

Exercise $\PageIndex{70}$

8a+5a+9

Exercise $\PageIndex{71}$

7p+6+5p−4

Answer: 12p+2

Exercise $\PageIndex{72}$

8x+7+4x−5

Translate an English Phrase to an Algebraic Expression

In the following exercises, translate the following phrases into algebraic expressions.

Exercise $\PageIndex{73}$

the sum of 8 and 12

Answer: 8+12

Exercise $\PageIndex{74}$

the sum of 9 and 1

Exercise $\PageIndex{75}$

the difference of x and 4

Answer: x−4

Exercise $\PageIndex{76}$

the difference of x and 3

Exercise $\PageIndex{77}$

the product of 6 and y

Answer: 6y

Exercise $\PageIndex{78}$

the product of 9 and y

Exercise $\PageIndex{79}$

Adele bought a skirt and a blouse. The skirt cost $15 more than the blouse. Let bb represent the cost of the blouse. Write an expression for the cost of the skirt.

Answer: b+15

Exercise $\PageIndex{80}$

Marcella has 6 fewer boy cousins than girl cousins. Let g represent the number of girl cousins. Write an expression for the number of boy cousins.

Add and Subtract Integers

Use Negatives and Opposites of Integers

In the following exercises, order each of the following pairs of numbers, using < or >.

Exercise $\PageIndex{81}$

6___2
−7___4
−9___−1
9___−3

Answer

Exercise $\PageIndex{82}$

−5___1
−4___−9
6___10
3___−8

In the following exercises,, find the opposite of each number.

Exercise $\PageIndex{83}$

−8
1

Answer

8
−1

Exercise $\PageIndex{84}$

−2
6

In the following exercises, simplify.

Exercise $\PageIndex{85}$

−(−19)

Answer: 19

Exercise $\PageIndex{86}$

−(−53)

In the following exercises, simplify.

Exercise $\PageIndex{87}$

−m when

m=3
m=−3

Answer

−3
3

Exercise $\PageIndex{88}$

−p when

p=6
p=−6

Simplify Expressions with Absolute Value

In the following exercises,, simplify.

Exercise $\PageIndex{89}$

|7|
|−25|
|0|

Answer

Exercise $\PageIndex{90}$

|5|
|0|
|−19|

In the following exercises, fill in <, >, or = for each of the following pairs of numbers.

Exercise $\PageIndex{91}$

−8___|−8|
−|−2|___−2

Answer

Exercise $\PageIndex{92}$

|−3|___−|−3|
4___−|−4|

In the following exercises, simplify.

Exercise $\PageIndex{93}$

|8−4|

Answer: 4

Exercise $\PageIndex{94}$

|9−6|

Exercise $\PageIndex{95}$

8(14−2|−2|)

Answer: 80

Exercise $\PageIndex{96}$

6(13−4|−2|)

In the following exercises, evaluate.

Exercise $\PageIndex{97}$

1. |x| when x=−28

Answer

Exercise $\PageIndex{98}$

∣y∣ when y=−37
|−z| when z=−24

Add Integers

In the following exercises, simplify each expression.

Exercise $\PageIndex{99}$

−200+65

Answer: −135

Exercise $\PageIndex{100}$

−150+45

Exercise $\PageIndex{101}$

2+(−8)+6

Answer: 0

Exercise $\PageIndex{102}$

4+(−9)+7

Exercise $\PageIndex{103}$

140+(−75)+67

Answer: 132

Exercise $\PageIndex{104}$

−32+24+(−6)+10

Subtract Integers

In the following exercises, simplify.

Exercise $\PageIndex{105}$

9−3

Answer: 6

Exercise $\PageIndex{106}$

−5−(−1)

Exercise $\PageIndex{107}$

15−6
15+(−6)

Answer

Exercise $\PageIndex{108}$

12−9
12+(−9)

Exercise $\PageIndex{109}$

8−(−9)
8+9

Answer

Exercise $\PageIndex{110}$

4−(−4)
4+4

In the following exercises, simplify each expression.

Exercise $\PageIndex{111}$

10−(−19)

Answer: 29

Exercise $\PageIndex{112}$

11−(−18)

Exercise $\PageIndex{113}$

31−79

Answer: −48

Exercise $\PageIndex{114}$

39−81

Exercise $\PageIndex{115}$

−31−11

Answer: −42

Exercise $\PageIndex{116}$

−32−18

Exercise $\PageIndex{117}$

−15−(−28)+5

Answer: 18

Exercise $\PageIndex{118}$

71+(−10)−8

Exercise $\PageIndex{119}$

−16−(−4+1)−7

Answer: -20

Exercise $\PageIndex{120}$

−15−(−6+4)−3

Multiply Integers

In the following exercises, multiply.

Exercise $\PageIndex{121}$

−5(7)

Answer: −35

Exercise $\PageIndex{122}$

−8(6)

Exercise $\PageIndex{123}$

−18(−2)

Answer: 36

Exercise $\PageIndex{124}$

−10(−6)

Divide Integers

In the following exercises, divide.

Exercise $\PageIndex{125}$

$-28 \div 7$

Answer: -4

Exercise $\PageIndex{126}$

$56 \div(-7)$

Exercise $\PageIndex{127}$

$-120 \div(-20)$

Answer: 6

Exercise $\PageIndex{128}$

$-200 \div 25$

Simplify Expressions with Integers

In the following exercises, simplify each expression.

Exercise $\PageIndex{129}$

−8(−2)−3(−9)

Answer: 43

Exercise $\PageIndex{130}$

−7(−4)−5(−3)

Exercise $\PageIndex{131}$

$(-5)^{3}$

Answer: −125

Exercise $\PageIndex{132}$

$(-4)^{3}$

Exercise $\PageIndex{133}$

$-4 \cdot 2 \cdot 11$

Answer: −88

Exercise $\PageIndex{134}$

$-5 \cdot 3 \cdot 10$

Exercise $\PageIndex{135}$

$-10(-4) \div(-8)$

Answer: -5

Exercise $\PageIndex{136}$

$-8(-6) \div(-4)$

Exercise $\PageIndex{137}$

31−4(3−9)

Answer: 55

Exercise $\PageIndex{138}$

24−3(2−10)

Evaluate Variable Expressions with Integers

In the following exercises, evaluate each expression.

Exercise $\PageIndex{139}$

x+8 when

x=−26
x=−95

Answer

−18
−87

Exercise $\PageIndex{140}$

y+9 when

y=−29
y=−84

Exercise $\PageIndex{141}$

When b=−11, evaluate:

b+6
−b+6

Answer

−5
17

Exercise $\PageIndex{142}$

When c=−9, evaluate:

c+(−4)c+(−4)
−c+(−4)

Exercise $\PageIndex{143}$

$p^{2}-5 p+2$ when
$p=-1$

Answer: 8

Exercise $\PageIndex{144}$

$q^{2}-2 q+9$ when $q=-2$

Exercise $\PageIndex{145}$

$6 x-5 y+15$ when $x=3$ and $y=-1$

Answer: 38

Exercise $\PageIndex{146}$

$3 p-2 q+9$ when $p=8$ and $q=-2$

Translate English Phrases to Algebraic Expressions

In the following exercises, translate to an algebraic expression and simplify if possible.

Exercise $\PageIndex{147}$

the sum of −4 and −17, increased by 32

Answer: (−4+(−17))+32;11

Exercise $\PageIndex{148}$

the difference of 15 and −7
subtract 15 from −7

Exercise $\PageIndex{149}$

the quotient of −45 and −9

Answer: $\frac{-45}{-9} ; 5$

Exercise $\PageIndex{150}$

the product of −12 and the difference of c and d

Use Integers in Applications

In the following exercises, solve.

Exercise $\PageIndex{151}$

Temperature The high temperature one day in Miami Beach, Florida, was 76°. That same day, the high temperature in Buffalo, New York was −8°. What was the difference between the temperature in Miami Beach and the temperature in Buffalo?

Answer: 84 degrees

Exercise $\PageIndex{152}$

Checking Account Adrianne has a balance of −$22 in her checking account. She deposits $301 to the account. What is the new balance?

Visualize Fractions

Find Equivalent Fractions

In the following exercises, find three fractions equivalent to the given fraction. Show your work, using figures or algebra.

Exercise $\PageIndex{153}$

$\frac{1}{4}$

Answer: $\frac{2}{8}, \frac{3}{12}, \frac{4}{16}$ answers may vary

Exercise $\PageIndex{154}$

$\frac{1}{3}$

Exercise $\PageIndex{155}$

$\frac{5}{6}$

Answer: $\frac{10}{12}, \frac{15}{18}, \frac{20}{24}$ answers may vary

Exercise $\PageIndex{156}$

$\frac{2}{7}$

Simplify Fractions

In the following exercises, simplify.

Exercise $\PageIndex{157}$

$\frac{7}{21}$

Answer: $\frac{1}{3}$

Exercise $\PageIndex{158}$

$\frac{8}{24}$

Exercise $\PageIndex{159}$

$\frac{15}{20}$

Answer: $\frac{3}{4}$

Exercise $\PageIndex{160}$

$\frac{12}{18}$

Exercise $\PageIndex{161}$

$-\frac{168}{192}$

Answer: $-\frac{7}{8}$

Exercise $\PageIndex{162}$

$-\frac{140}{224}$

Exercise $\PageIndex{163}$

$\frac{11 x}{11 y}$

Answer: $\frac{x}{y}$

Exercise $\PageIndex{164}$

$\frac{15 a}{15 b}$

Multiply Fractions

In the following exercises, multiply.

Exercise $\PageIndex{165}$

$\frac{2}{5} \cdot \frac{1}{3}$

Answer: $\frac{2}{15}$

Exercise $\PageIndex{166}$

$\frac{1}{2} \cdot \frac{3}{8}$

Exercise $\PageIndex{167}$

$\frac{7}{12}\left(-\frac{8}{21}\right)$

Answer: $-\frac{2}{9}$

Exercise $\PageIndex{168}$

$\frac{5}{12}\left(-\frac{8}{15}\right)$

Exercise $\PageIndex{169}$

$-28 p\left(-\frac{1}{4}\right)$

Answer: 7p

Exercise $\PageIndex{170}$

$-51 q\left(-\frac{1}{3}\right)$

Exercise $\PageIndex{172}$

$\frac{14}{5}(-15)$

Answer: −42

Exercise $\PageIndex{173}$

$-1\left(-\frac{3}{8}\right)$

Divide Fractions

In the following exercises, divide

Exercise $\PageIndex{174}$

$\frac{1}{2} \div \frac{1}{4}$

Answer: 2

Exercise $\PageIndex{175}$

$\frac{1}{2} \div \frac{1}{8}$

Exercise $\PageIndex{176}$

$-\frac{4}{5} \div \frac{4}{7}$

Answer: $-\frac{7}{5}$

Exercise $\PageIndex{177}$

$-\frac{3}{4} \div \frac{3}{5}$

Exercise $\PageIndex{178}$

$\frac{5}{8} \div \frac{a}{10}$

Answer: $\frac{25}{4 a}$

Exercise $\PageIndex{179}$

$\frac{5}{6} \div \frac{c}{15}$

Exercise $\PageIndex{180}$

$\frac{7 p}{12} \div \frac{21 p}{8}$

Answer: $\frac{2}{9}$

Exercise $\PageIndex{181}$

$\frac{5 q}{12} \div \frac{15 q}{8}$

Exercise $\PageIndex{182}$

$\frac{2}{5} \div(-10)$

Answer: $-\frac{1}{25}$

Exercise $\PageIndex{183}$

$-18 \div-\left(\frac{9}{2}\right)$

In the following exercises, simplify.

Exercise $\PageIndex{184}$

$\frac{\frac{2}{3}}{\frac{8}{9}}$

Answer: $\frac{3}{4}$

Exercise $\PageIndex{185}$

$\frac{\frac{4}{5}}{\frac{8}{15}}$

Exercise $\PageIndex{186}$

$\frac{-\frac{9}{10}}{3}$

Answer: $-\frac{3}{10}$

Exercise $\PageIndex{187}$

$\frac{2}{\frac{5}{8}}$

Exercise $\PageIndex{188}$

$\frac{\frac{r}{5}}{\frac{s}{3}}$

Answer: $\frac{3 r}{5 s}$

Exercise $\PageIndex{189}$

$\frac{-\frac{x}{6}}{-\frac{8}{9}}$

Simplify Expressions Written with a Fraction Bar

In the following exercises, simplify.

Exercise $\PageIndex{190}$

$\frac{4+11}{8}$

Answer: $\frac{15}{8}$

Exercise $\PageIndex{191}$

$\frac{9+3}{7}$

Exercise $\PageIndex{192}$

$\frac{30}{7-12}$

Answer: -6

Exercise $\PageIndex{193}$

$\frac{15}{4-9}$

Exercise $\PageIndex{194}$

$\frac{22-14}{19-13}$

Answer: $\frac{4}{3}$

Exercise $\PageIndex{195}$

$\frac{15+9}{18+12}$

Exercise $\PageIndex{196}$

$\frac{5 \cdot 8}{-10}$

Answer: -4

Exercise $\PageIndex{197}$

$\frac{3 \cdot 4}{-24}$

Exercise $\PageIndex{198}$

$\frac{15 \cdot 5-5^{2}}{2 \cdot 10}$

Answer: $\frac{5}{2}$

Exercise $\PageIndex{199}$

$\frac{12 \cdot 9-3^{2}}{3 \cdot 18}$

Exercise $\PageIndex{200}$

$\frac{2+4(3)}{-3-2^{2}}$

Answer: -2

Exercise $\PageIndex{201}$

$\frac{7+3(5)}{-2-3^{2}}$

Translate Phrases to Expressions with Fractions

In the following exercises, translate each English phrase into an algebraic expression.

Exercise $\PageIndex{202}$

the quotient of c and the sum of d and 9.

Answer: $\frac{c}{d+9}$

Exercise $\PageIndex{203}$

the quotient of the difference of h and k, and −5.

Add and Subtract Fractions

Add and Subtract Fractions with a Common Denominator

In the following exercises, add.

Exercise $\PageIndex{204}$

$\frac{4}{9}+\frac{1}{9}$

Answer: $\frac{5}{9}$

Exercise $\PageIndex{205}$

$\frac{2}{9}+\frac{5}{9}$

Exercise $\PageIndex{206}$

$\frac{y}{3}+\frac{2}{3}$

Answer: $\frac{y+2}{3}$

Exercise $\PageIndex{207}$

$\frac{7}{p}+\frac{9}{p}$

Exercise $\PageIndex{208}$

$-\frac{1}{8}+\left(-\frac{3}{8}\right)$

Answer: $-\frac{1}{2}$

Exercise $\PageIndex{209}$

$-\frac{1}{8}+\left(-\frac{5}{8}\right)$

In the following exercises, subtract.

Exercise $\PageIndex{210}$

$\frac{4}{5}-\frac{1}{5}$

Answer: $\frac{3}{5}$

Exercise $\PageIndex{211}$

$\frac{4}{5}-\frac{3}{5}$

Exercise $\PageIndex{212}$

$\frac{y}{17}-\frac{9}{17}$

Answer: $\frac{y-9}{17}$

Exercise $\PageIndex{213}$

$\frac{x}{19}-\frac{8}{19}$

Exercise $\PageIndex{214}$

$-\frac{8}{d}-\frac{3}{d}$

Answer: $-\frac{11}{d}$

Exercise $\PageIndex{215}$

$-\frac{7}{c}-\frac{7}{c}$

Add or Subtract Fractions with Different Denominators

In the following exercises, add or subtract.

Exercise $\PageIndex{216}$

$\frac{1}{3}+\frac{1}{5}$

Answer: $\frac{8}{15}$

Exercise $\PageIndex{217}$

$\frac{1}{4}+\frac{1}{5}$

Exercise $\PageIndex{218}$

$\frac{1}{5}-\left(-\frac{1}{10}\right)$

Answer: $\frac{3}{10}$

Exercise $\PageIndex{219}$

$\frac{1}{2}-\left(-\frac{1}{6}\right)$

Exercise $\PageIndex{220}$

$\frac{2}{3}+\frac{3}{4}$

Answer: $\frac{17}{12}$

Exercise $\PageIndex{221}$

$\frac{3}{4}+\frac{2}{5}$

Exercise $\PageIndex{222}$

$\frac{11}{12}-\frac{3}{8}$

Answer: $\frac{13}{24}$

Exercise $\PageIndex{223}$

$\frac{5}{8}-\frac{7}{12}$

Exercise $\PageIndex{224}$

$-\frac{9}{16}-\left(-\frac{4}{5}\right)$

Answer: $\frac{19}{80}$

Exercise $\PageIndex{225}$

$-\frac{7}{20}-\left(-\frac{5}{8}\right)$

Exercise $\PageIndex{226}$

$1+\frac{5}{6}$

Answer: $\frac{11}{6}$

Exercise $\PageIndex{227}$

$1-\frac{5}{9}$

Use the Order of Operations to Simplify Complex Fractions

In the following exercises, simplify.

Exercise $\PageIndex{228}$

$\frac{\left(\frac{1}{5}\right)^{2}}{2+3^{2}}$

Answer: $\frac{1}{275}$

Exercise $\PageIndex{229}$

$\frac{\left(\frac{1}{3}\right)^{2}}{5+2^{2}}$

Exercise $\PageIndex{230}$

$\frac{\frac{2}{3}+\frac{1}{2}}{\frac{3}{4}-\frac{2}{3}}$

Answer: 14

Exercise $\PageIndex{231}$

$\frac{\frac{3}{4}+\frac{1}{2}}{\frac{5}{6}-\frac{2}{3}}$

Evaluate Variable Expressions with Fractions

In the following exercises, evaluate.

Exercise $\PageIndex{232}$

$x+\frac{1}{2}$ when

$x=-\frac{1}{8}$
$x=-\frac{1}{2}$

Answer

$\frac{3}{8}$
$0$

Exercise $\PageIndex{233}$

$x+\frac{2}{3}$ when

$x=-\frac{1}{6}$
$x=-\frac{5}{3}$

Exercise $\PageIndex{234}$

4$p^{2} q$ when $p=-\frac{1}{2}$ and $q=\frac{5}{9}$

Answer: $\frac{5}{9}$

Exercise $\PageIndex{235}$

5$m^{2} n$ when $m=-\frac{2}{5}$ and $n=\frac{1}{3}$

Exercise $\PageIndex{236}$

$\frac{u+v}{w}$ when
$u=-4, v=-8, w=2$

Answer: -6

Exercise $\PageIndex{237}$

$\frac{m+n}{p}$ when
$m=-6, n=-2, p=4$

Decimals

Name and Write Decimals

In the following exercises, write as a decimal.

Exercise $\PageIndex{238}$

Eight and three hundredths

Answer: 8.03

Exercise $\PageIndex{239}$

Nine and seven hundredths

Exercise $\PageIndex{240}$

One thousandth

Answer: 0.001

Exercise $\PageIndex{241}$

Nine thousandths

In the following exercises, name each decimal.

Exercise $\PageIndex{242}$

7.8

Answer: seven and eight tenths

Exercise $\PageIndex{243}$

5.01

Exercise $\PageIndex{244}$

0.005

Answer: five thousandths

Exercise $\PageIndex{245}$

0.381

Round Decimals

In the following exercises, round each number to the nearest

hundredth
tenth
whole number.

Exercise $\PageIndex{246}$

5.7932

Answer

5.79
5.8
6

Exercise $\PageIndex{247}$

3.6284

Exercise $\PageIndex{248}$

12.4768

Answer

12.48
12.5
12

Exercise $\PageIndex{249}$

25.8449

Add and Subtract Decimals

In the following exercises, add or subtract.

Exercise $\PageIndex{250}$

18.37+9.36

Answer: 27.73

Exercise $\PageIndex{251}$

256.37−85.49

Exercise $\PageIndex{252}$

15.35−20.88

Answer: −5.53

Exercise $\PageIndex{253}$

37.5+12.23

Exercise $\PageIndex{254}$

−4.2+(−9.3)

Answer: −13.5

Exercise $\PageIndex{255}$

−8.6+(−8.6)

Exercise $\PageIndex{256}$

100−64.2

Answer: 35.8

Exercise $\PageIndex{257}$

100−65.83

Exercise $\PageIndex{258}$

2.51+40

Answer: 42.51

Exercise $\PageIndex{259}$

9.38+60

Multiply and Divide Decimals

In the following exercises, multiply.

Exercise $\PageIndex{260}$

(0.3)(0.4)

Answer: 0.12

Exercise $\PageIndex{261}$

(0.6)(0.7)

Exercise $\PageIndex{262}$

(8.52)(3.14)

Answer: 26.7528

Exercise $\PageIndex{263}$

(5.32)(4.86)

Exercise $\PageIndex{264}$

(0.09)(24.78)

Answer: 2.2302

Exercise $\PageIndex{265}$

(0.04)(36.89)

In the following exercises, divide.

Exercise $\PageIndex{266}$

$0.15 \div 5$

Answer: 0.03

Exercise $\PageIndex{267}$

$0.27 \div 3$

Exercise $\PageIndex{268}$

$\$ 8.49 \div 12$

Answer: $0.71

Exercise $\PageIndex{269}$

$\$ 16.99 \div 9$

Exercise $\PageIndex{270}$

$12 \div 0.08$

Answer: 150

Exercise $\PageIndex{271}$

$5 \div 0.04$

Convert Decimals, Fractions, and Percents

In the following exercises, write each decimal as a fraction.

Exercise $\PageIndex{272}$

0.08

Answer: $\frac{2}{25}$

Exercise $\PageIndex{273}$

0.17

Exercise $\PageIndex{274}$

0.425

Answer: $\frac{17}{40}$

Exercise $\PageIndex{275}$

0.184

Exercise $\PageIndex{276}$

1.75

Answer: $\frac{7}{4}$

Exercise $\PageIndex{277}$

0.035

In the following exercises, convert each fraction to a decimal.

Exercise $\PageIndex{278}$

$\frac{2}{5}$

Answer: 0.4

Exercise $\PageIndex{279}$

$\frac{4}{5}$

Exercise $\PageIndex{280}$

$-\frac{3}{8}$

Answer: −0.375

Exercise $\PageIndex{281}$

$-\frac{5}{8}$

Exercise $\PageIndex{282}$

$\frac{5}{9}$

Answer: $0 . \overline{5}$

Exercise $\PageIndex{283}$

$\frac{2}{9}$

Exercise $\PageIndex{284}$

$\frac{1}{2}+6.5$

Answer: 7

Exercise $\PageIndex{285}$

$\frac{1}{4}+10.75$

In the following exercises, convert each percent to a decimal.

Exercise $\PageIndex{286}$

Answer: 0.05

Exercise $\PageIndex{287}$

Exercise $\PageIndex{288}$

40%

Answer: 0.4

Exercise $\PageIndex{289}$

50%

Exercise $\PageIndex{290}$

115%

Answer: 1.15

Exercise $\PageIndex{291}$

125%

In the following exercises, convert each decimal to a percent.

Exercise $\PageIndex{292}$

0.18

Answer: 18%

Exercise $\PageIndex{293}$

0.15

Exercise $\PageIndex{294}$

0.009

Answer: 0.9%

Exercise $\PageIndex{295}$

0.008

Exercise $\PageIndex{296}$

1.5

Answer: 150%

Exercise $\PageIndex{297}$

2.2

The Real Numbers

Simplify Expressions with Square Roots

In the following exercises, simplify.

Exercise $\PageIndex{298}$

$\sqrt{64}$

Answer: 8

Exercise $\PageIndex{299}$

$\sqrt{144}$

Exercise $\PageIndex{300}$

$-\sqrt{25}$

Answer: -5

Exercise $\PageIndex{301}$

$-\sqrt{81}$

Identify Integers, Rational Numbers, Irrational Numbers, and Real Numbers

In the following exercises, write as the ratio of two integers.

Exercise $\PageIndex{302}$

9
8.47

Answer

$\frac{9}{1}$
$\frac{847}{100}$

Exercise $\PageIndex{303}$

−15
3.591

In the following exercises, list the

rational numbers,
irrational numbers.

Exercise $\PageIndex{304}$

$0.84,0.79132 \ldots, 1 . \overline{3}$

Answer

$0.84,1.3$
$0.79132 \ldots$

Exercise $\PageIndex{305}$

$2.3 \overline{8}, 0.572,4.93814 \ldots$

In the following exercises, identify whether each number is rational or irrational.

Exercise $\PageIndex{306}$

$\sqrt{121}$
$\sqrt{48}$

Answer

rational
irrational

Exercise $\PageIndex{307}$

$\sqrt{56}$
$\sqrt{16}$

In the following exercises, identify whether each number is a real number or not a real number.

Exercise $\PageIndex{308}$

$\sqrt{-9}$
$-\sqrt{169}$

Answer

not a real number
real number

Exercise $\PageIndex{309}$

$\sqrt{-64}$
$-\sqrt{81}$

In the following exercises, list the

whole numbers,
integers,
rational numbers,
irrational numbers,
real numbers for each set of numbers.

Exercise $\PageIndex{310}$

$-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots$

Answer

$0, \sqrt{16}$
$-4,0, \sqrt{16}$
$-4,0, \frac{5}{6}, \sqrt{16}$
$\sqrt{18}, 5.2537 \ldots$
$-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots$

Exercise $\PageIndex{311}$

$-\sqrt{4}, 0 . \overline{36}, \frac{13}{3}, 6.9152 \ldots, \sqrt{48}, 10 \frac{1}{2}$

Locate Fractions on the Number Line

In the following exercises, locate the numbers on a number line.

Exercise $\PageIndex{312}$

$\frac{2}{3}, \frac{5}{4}, \frac{12}{5}$

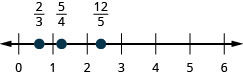
Answer: $This figure is a number line ranging from 0 to 6 with tick marks for each integer. 2 thirds, 5 fourths, and 12 fifths are plotted.$

Exercise $\PageIndex{313}$

$\frac{1}{3}, \frac{7}{4}, \frac{13}{5}$

Exercise $\PageIndex{314}$

$2 \frac{1}{3},-2 \frac{1}{3}$

Answer

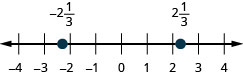
Exercise $\PageIndex{315}$

$1 \frac{3}{5},-1 \frac{3}{5}$

In the following exercises, order each of the following pairs of numbers, using < or >.

Exercise $\PageIndex{316}$

−1___$-\frac{1}{8}$

Answer: <

Exercise $\PageIndex{317}$

$-3 \frac{1}{4}$___−4

Exercise $\PageIndex{318}$

$-\frac{7}{9}$ ___ $\frac{4}{9}$

Answer: >

Exercise $\PageIndex{319}$

$-2$ ___ $\frac{19}{8}$

Locate Decimals on the Number Line

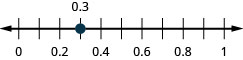
In the following exercises, locate on the number line.

Exercise $\PageIndex{320}$

0.3

Answer

Exercise $\PageIndex{321}$

−0.2

Exercise $\PageIndex{322}$

−2.5

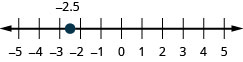
Answer: $This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. Negative 2.5 is plotted.$

Exercise $\PageIndex{323}$

2.7

In the following exercises, order each of the following pairs of numbers, using < or >.

Exercise $\PageIndex{324}$

0.9___0.6

Answer: >

Exercise $\PageIndex{325}$

0.7___0.8

Exercise $\PageIndex{326}$

−0.6___−0.59

Answer: >

Exercise $\PageIndex{327}$

−0.27___−0.3

Properties of Real Numbers

Use the Commutative and Associative Properties

In the following exercises, use the Associative Property to simplify.

Exercise $\PageIndex{328}$

−12(4m)

Answer: −48m

Exercise $\PageIndex{329}$

30$\left(\frac{5}{6} q\right)$

Exercise $\PageIndex{330}$

(a+16)+31

Answer: a+47

Exercise $\PageIndex{331}$

(c+0.2)+0.7

In the following exercises, simplify.

Exercise $\PageIndex{332}$

6y+37+(−6y)

Answer: 37

Exercise $\PageIndex{333}$

$\frac{1}{4}+\frac{11}{15}+\left(-\frac{1}{4}\right)$

Exercise $\PageIndex{334}$

$\frac{14}{11} \cdot \frac{35}{9} \cdot \frac{14}{11}$

Answer: $\frac{35}{9}$

Exercise $\PageIndex{335}$

$-18 \cdot 15 \cdot \frac{2}{9}$

Exercise $\PageIndex{336}$

$\left(\frac{7}{12}+\frac{4}{5}\right)+\frac{1}{5}$

Answer: 1$\frac{7}{12}$

Exercise $\PageIndex{337}$

(3.98d+0.75d)+1.25d

Exercise $\PageIndex{338}$

11x+8y+16x+15y

Answer: 27x+23y

Exercise $\PageIndex{339}$

52m+(−20n)+(−18m)+(−5n)

Use the Identity and Inverse Properties of Addition and Multiplication

In the following exercises, find the additive inverse of each number.

Exercise $\PageIndex{340}$

$\frac{1}{3}$
5.1
$-14$
$-\frac{8}{5}$

Answer

$-\frac{1}{3}$
$-5.1$
-14
$-\frac{8}{5}$

Exercise $\PageIndex{341}$

$-\frac{7}{8}$
$-0.03$
17
$\frac{12}{5}$

In the following exercises, find the multiplicative inverse of each number.

Exercise $\PageIndex{342}$

$10$
$-\frac{4}{9}$
0.6

Answer

$\frac{1}{10}$
$-\frac{9}{4}$
$\frac{5}{3}$

Exercise $\PageIndex{343}$

$-\frac{9}{2}$
-7
2.1

Use the Properties of Zero

In the following exercises, simplify.

Exercise $\PageIndex{344}$

83$\cdot 0$

Answer: 0

Exercise $\PageIndex{345}$

$\frac{0}{9}$

Exercise $\PageIndex{346}$

$\frac{5}{0}$

Answer: undefined

Exercise $\PageIndex{347}$

$0 \div \frac{2}{3}$

In the following exercises, simplify.

Exercise $\PageIndex{348}$

43+39+(−43)

Answer: 39

Exercise $\PageIndex{349}$

(n+6.75)+0.25

Exercise $\PageIndex{350}$

$\frac{5}{13} \cdot 57 \cdot \frac{13}{5}$

Answer: 57

Exercise $\PageIndex{351}$

$\frac{1}{6} \cdot 17 \cdot 12$

Exercise $\PageIndex{352}$

$\frac{2}{3} \cdot 28 \cdot \frac{3}{7}$

Answer: 8

Exercise $\PageIndex{353}$

$9(6 x-11)+15$

Simplify Expressions Using the Distributive Property

In the following exercises, simplify using the Distributive Property.

Exercise $\PageIndex{354}$

7(x+9)

Answer: 7x+63

Exercise $\PageIndex{355}$

9(u−4)

Exercise $\PageIndex{356}$

−3(6m−1)

Answer: −18m+3

Exercise $\PageIndex{357}$

−8(−7a−12)

Exercise $\PageIndex{358}$

$\frac{1}{3}(15 n-6)$

Answer: 5n−2

Exercise $\PageIndex{359}$

$(y+10) \cdot p$

Exercise $\PageIndex{360}$

(a−4)−(6a+9)

Answer: −5a−13

Exercise $\PageIndex{361}$

4(x+3)−8(x−7)

Systems of Measurement

1.1 Define U.S. Units of Measurement and Convert from One Unit to Another

In the following exercises, convert the units. Round to the nearest tenth.

Exercise $\PageIndex{362}$

A floral arbor is 7 feet tall. Convert the height to inches.

Answer: 84 inches

Exercise $\PageIndex{363}$

A picture frame is 42 inches wide. Convert the width to feet.

Exercise $\PageIndex{364}$

Kelly is 5 feet 4 inches tall. Convert her height to inches.

Answer: 64 inches

Exercise $\PageIndex{365}$

A playground is 45 feet wide. Convert the width to yards.

Exercise $\PageIndex{366}$

The height of Mount Shasta is 14,179 feet. Convert the height to miles.

Answer: 2.7 miles

Exercise $\PageIndex{367}$

Shamu weights 4.5 tons. Convert the weight to pounds.

Exercise $\PageIndex{368}$

The play lasted $1\frac{3}{4}$ hours. Convert the time to minutes.

Answer: 105 minutes

Exercise $\PageIndex{369}$

How many tablespoons are in a quart?

Exercise $\PageIndex{370}$

Naomi’s baby weighed 5 pounds 14 ounces at birth. Convert the weight to ounces.

Answer: 94 ounces

Exercise $\PageIndex{371}$

Trinh needs 30 cups of paint for her class art project. Convert the volume to gallons.

Use Mixed Units of Measurement in the U.S. System.

In the following exercises, solve.

Exercise $\PageIndex{372}$

John caught 4 lobsters. The weights of the lobsters were 1 pound 9 ounces, 1 pound 12 ounces, 4 pounds 2 ounces, and 2 pounds 15 ounces. What was the total weight of the lobsters?

Answer: 10 lbs. 6 oz.

Exercise $\PageIndex{373}$

Every day last week Pedro recorded the number of minutes he spent reading. The number of minutes were 50, 25, 83, 45, 32, 60, 135. How many hours did Pedro spend reading?

Exercise $\PageIndex{374}$

Fouad is 6 feet 2 inches tall. If he stands on a rung of a ladder 8 feet 10 inches high, how high off the ground is the top of Fouad’s head?

Answer: 15 feet

Exercise $\PageIndex{375}$

Dalila wants to make throw pillow covers. Each cover takes 30 inches of fabric. How many yards of fabric does she need for 4 covers?

Make Unit Conversions in the Metric System

In the following exercises, convert the units.

Exercise $\PageIndex{376}$

Donna is 1.7 meters tall. Convert her height to centimeters.

Answer: 170 centimeters

Exercise $\PageIndex{377}$

Mount Everest is 8,850 meters tall. Convert the height to kilometers.

Exercise $\PageIndex{378}$

One cup of yogurt contains 488 milligrams of calcium. Convert this to grams.

Answer: 0.488 grams

Exercise $\PageIndex{379}$

One cup of yogurt contains 13 grams of protein. Convert this to milligrams.

Exercise $\PageIndex{380}$

Sergio weighed 2.9 kilograms at birth. Convert this to grams.

Answer: 2,900 grams

Exercise $\PageIndex{381}$

A bottle of water contained 650 milliliters. Convert this to liters.

Use Mixed Units of Measurement in the Metric System

In the following exerices, solve.

Exercise $\PageIndex{382}$

Minh is 2 meters tall. His daughter is 88 centimeters tall. How much taller is Minh than his daughter?

Answer: 1.12 meter

Exercise $\PageIndex{383}$

Selma had a 1 liter bottle of water. If she drank 145 milliliters, how much water was left in the bottle?

Exercise $\PageIndex{384}$

One serving of cranberry juice contains 30 grams of sugar. How many kilograms of sugar are in 30 servings of cranberry juice?

Answer: 0.9 kilograms

Exercise $\PageIndex{385}$

One ounce of tofu provided 2 grams of protein. How many milligrams of protein are provided by 5 ounces of tofu?

Convert between the U.S. and the Metric Systems of Measurement

In the following exercises, make the unit conversions. Round to the nearest tenth.

Exercise $\PageIndex{386}$

Majid is 69 inches tall. Convert his height to centimeters.

Answer: 175.3 centimeters

Exercise $\PageIndex{387}$

A college basketball court is 84 feet long. Convert this length to meters.

Exercise $\PageIndex{388}$

Caroline walked 2.5 kilometers. Convert this length to miles.

Answer: 1.6 miles

Exercise $\PageIndex{389}$

Lucas weighs 78 kilograms. Convert his weight to pounds.

Exercise $\PageIndex{390}$

Steve’s car holds 55 liters of gas. Convert this to gallons.

Answer: 14.6 gallons

Exercise $\PageIndex{391}$

A box of books weighs 25 pounds. Convert the weight to kilograms.

Convert between Fahrenheit and Celsius Temperatures

In the following exercises, convert the Fahrenheit temperatures to degrees Celsius. Round to the nearest tenth.

Exercise $\PageIndex{392}$

95° Fahrenheit

Answer: 35° C

Exercise $\PageIndex{393}$

23° Fahrenheit

Exercise $\PageIndex{394}$

20° Fahrenheit

Answer: –6.7° C

Exercise $\PageIndex{395}$

64° Fahrenheit

In the following exercises, convert the Celsius temperatures to degrees Fahrenheit. Round to the nearest tenth.

Exercise $\PageIndex{396}$

30° Celsius

Answer: 86° F

Exercise $\PageIndex{397}$

–5° Celsius

Exercise $\PageIndex{398}$

–12° Celsius

Answer: 10.4° F

Exercise $\PageIndex{399}$

24° Celsius

Chapter Practice Test

Exercise $\PageIndex{1}$

Write as a whole number using digits: two hundred five thousand, six hundred seventeen.

Answer: 205,617

Exercise $\PageIndex{2}$

Find the prime factorization of 504.

Exercise $\PageIndex{3}$

Find the Least Common Multiple of 18 and 24.

Answer: 72

Exercise $\PageIndex{4}$

Combine like terms: 5n+8+2n−1.

In the following exercises, evaluate.

Exercise $\PageIndex{5}$

$-|x|$ when $x=-2$

Answer: −2

Exercise $\PageIndex{6}$

11−a when a=−3

Exercise $\PageIndex{7}$

Translate to an algebraic expression and simplify: twenty less than negative 7.

Answer: −7−20;−27

Exercise $\PageIndex{8}$

Monique has a balance of −$18 in her checking account. She deposits $152 to the account. What is the new balance?

Exercise $\PageIndex{9}$

Round 677.1348 to the nearest hundredth.

Answer: 677.13

Exercise $\PageIndex{10}$

Convert $\frac{4}{5}$ to a decimal.

Exercise $\PageIndex{11}$

Convert 1.85 to a percent.

Answer: 185%

Exercise $\PageIndex{12}$

Locate $\frac{2}{3},-1.5,$ and $\frac{9}{4}$ on a number line.

In the following exercises, simplify each expression.

Exercise $\PageIndex{13}$

$4+10(3+9)-5^{2}$

Answer: 99

Exercise $\PageIndex{14}$

−85+42

Exercise $\PageIndex{15}$

−19−25

Answer: −44

Exercise $\PageIndex{16}$

$(-2)^{4}$

Exercise $\PageIndex{17}$

$-5(-9) \div 15$

Answer: 3

Exercise $\PageIndex{18}$

$\frac{3}{8} \cdot \frac{11}{12}$

Exercise $\PageIndex{19}$

$\frac{4}{5} \div \frac{9}{20}$

Answer: $\frac{16}{9}$

Exercise $\PageIndex{20}$

$\frac{12+3 \cdot 5}{15-6}$

Exercise $\PageIndex{21}$

$\frac{m}{7}+\frac{10}{7}$

Answer: $\frac{m+10}{7}$

Exercise $\PageIndex{22}$

$\frac{7}{12}-\frac{3}{8}$

Exercise $\PageIndex{23}$

$-5.8+(-4.7)$

Answer: −10.5

Exercise $\PageIndex{24}$

100−64.25

Exercise $\PageIndex{25}$

(0.07)(31.95)

Answer: 2.2365

Exercise $\PageIndex{26}$

$9 \div 0.05$

Exercise $\PageIndex{27}$

$-14\left(\frac{5}{7} p\right)$

Answer: −10p

Exercise $\PageIndex{28}$

(u+8)−9

Exercise $\PageIndex{29}$

6x+(−4y)+9x+8y

Answer: 15x+4y

Exercise $\PageIndex{30}$

$\frac{0}{23}$

Exercise $\PageIndex{31}$

$\frac{75}{0}$

Answer: undefined

Exercise $\PageIndex{32}$

−2(13q−5)

Exercise $\PageIndex{33}$

A movie lasted 1$\frac{2}{3}$ hours. How many minutes did it last? ( 1 hour $=60$ minutes)

Answer: 100 minutes

Exercise $\PageIndex{34}$

Mike’s SUV is 5 feet 11 inches tall. He wants to put a rooftop cargo bag on the the SUV. The cargo bag is 1 foot 6 inches tall. What will the total height be of the SUV with the cargo bag on the roof? (1 foot = 12 inches)

Exercise $\PageIndex{35}$

Jennifer ran 2.8 miles. Convert this length to kilometers. (1 mile = 1.61 kilometers)

Answer: 4.508 km