5.1E: Exercises

Practice Makes Perfect

Determine Whether an Ordered Pair is a Solution of a System of Equations. In the following exercises, determine if the following points are solutions to the given system of equations.

Exercise $\PageIndex{1}$

$\begin{cases}{2x−6y=0} \\ {3x−4y=5}\end{cases}$

1. (3,1)
2. (−3,4)

Answer

1. yes
2. no

Exercise $\PageIndex{2}$

$\begin{cases}{7x-4y=-1} \\ {-3x-2y = 1} \end{cases}$

1. ($-\frac{3}{13}$, $-\frac{2}{13}$)
2. (1,-2)

Answer

1. yes
2. no

Exercise $\PageIndex{3}$

$\left\{\begin{array}{l}{2 x+y=5} \\ {x+y=1}\end{array}\right.$

1. (4,−3)
2. (2,0)

Answer

1. yes
2. no

Exercise $\PageIndex{4}$

$\left\{\begin{array}{l}{-3 x+y=8} \\ {-x+2 y=-9}\end{array}\right.$

1. (−5,−7)
2. (−5,7)

Exercise $\PageIndex{5}$

$\left\{\begin{array}{l}{x+y=2} \\ {y=\frac{3}{4} x}\end{array}\right.$

1. $\left(\frac{8}{7}, \frac{6}{7}\right)$
2. $\left(1, \frac{3}{4}\right)$

Answer

1. yes
2. no

Exercise $\PageIndex{6}$

$\left\{\begin{array}{l}{x+y=1} \\ {y=\frac{2}{5} x}\end{array}\right.$

1. $\left(\frac{5}{7}, \frac{2}{7}\right)$
2. (5,2)

Exercise $\PageIndex{7}$

$\left\{\begin{array}{l}{x+5 y=10} \\ {y=\frac{3}{5} x+1}\end{array}\right.$

1. (−10,4)
2. $\left(\frac{5}{4}, \frac{7}{4}\right)$

Answer

1. no
2. yes

Exercise $\PageIndex{8}$

$\left\{\begin{array}{l}{x+3 y=9} \\ {y=\frac{2}{3} x-2}\end{array}\right.$

1. (−6,5)
2. $\left(5, \frac{4}{3}\right)$

Solve a System of Linear Equations by Graphing In the following exercises, solve the following systems of equations by graphing.

Exercise $\PageIndex{9}$

$\left\{\begin{array}{l}{3 x+y=-3} \\ {2 x+3 y=5}\end{array}\right.$

Answer

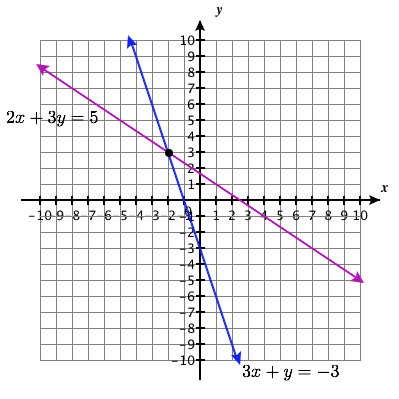
Solution Point: $(-2,3)$

Exercise $\PageIndex{10}$

$\left\{\begin{array}{l}{-x+y=2} \\ {2 x+y=-4}\end{array}\right.$

Exercise $\PageIndex{11}$

$\left\{\begin{array}{l}{-3 x+y=-1} \\ {2 x+y=4}\end{array}\right.$

Answer

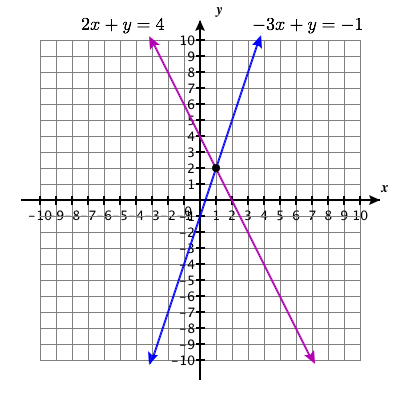
Solution Point: $(1,2)$

Exercise $\PageIndex{12}$

$\left\{\begin{array}{l}{-2 x+3 y=-3} \\ {x+y=4}\end{array}\right.$

Exercise $\PageIndex{13}$

$\left\{\begin{array}{l}{y=x+2} \\ {y=-2 x+2}\end{array}\right.$

Answer

Solution Point: $(0,2)$

Exercise $\PageIndex{14}$

$\left\{\begin{array}{l}{y=x-2} \\ {y=-3 x+2}\end{array}\right.$

Exercise $\PageIndex{15}$

$\left\{\begin{array}{l}{y=\frac{3}{2} x+1} \\ {y=-\frac{1}{2} x+5}\end{array}\right.$

Answer

Solution Point: $(2,4)$

Exercise $\PageIndex{16}$

$\left\{\begin{array}{l}{y=\frac{2}{3} x-2} \\ {y=-\frac{1}{3} x-5}\end{array}\right.$

Exercise $\PageIndex{17}$

$\left\{\begin{array}{l}{-x+y=-3} \\ {4 x+4 y=4}\end{array}\right.$

Answer

Solution Point: $(2,-1)$

Exercise $\PageIndex{18}$

$\left\{\begin{array}{l}{x-y=3} \\ {2 x-y=4}\end{array}\right.$

Exercise $\PageIndex{19}$

$\left\{\begin{array}{l}{-3 x+y=-1} \\ {2 x+y=4}\end{array}\right.$

Answer

Solution Point: $(1,2)$

Exercise $\PageIndex{20}$

$\left\{\begin{array}{l}{-3 x+y=-2} \\ {4 x-2 y=6}\end{array}\right.$

Exercise $\PageIndex{21}$

$\left\{\begin{array}{l}{x+y=5} \\ {2 x-y=4}\end{array}\right.$

Answer

Solution Point: $(3,2)$

Exercise $\PageIndex{22}$

$\left\{\begin{array}{l}{x-y=2} \\ {2 x-y=6}\end{array}\right.$

Exercise $\PageIndex{23}$

$\left\{\begin{array}{l}{x+y=2} \\ {x-y=0}\end{array}\right.$

Answer

Solution Point: $(1,1)$

Exercise $\PageIndex{24}$

$\left\{\begin{array}{l}{x+y=6} \\ {x-y=-8}\end{array}\right.$

Exercise $\PageIndex{25}$

$\left\{\begin{array}{l}{x+y=-5} \\ {x-y=3}\end{array}\right.$

Answer

Solution Point: $(-1,-4)$

Exercise $\PageIndex{26}$

$\left\{\begin{array}{l}{x+y=4} \\ {x-y=0}\end{array}\right.$

Exercise $\PageIndex{27}$

$\left\{\begin{array}{l}{x+y=-4} \\ {-x+2 y=-2}\end{array}\right.$

Answer

Solution Point: $(3,3)$

Exercise $\PageIndex{28}$

$\left\{\begin{array}{l}{-x+3 y=3} \\ {x+3 y=3}\end{array}\right.$

Exercise $\PageIndex{29}$

$\left\{\begin{array}{l}{-2 x+3 y=3} \\ {x+3 y=12}\end{array}\right.$

Answer

Solution Point: $(-5,6)$

Exercise $\PageIndex{30}$

$\left\{\begin{array}{l}{2 x-y=4} \\ {2 x+3 y=12}\end{array}\right.$

Exercise $\PageIndex{31}$

$\left\{\begin{array}{l}{2 x+3 y=6} \\ {y=-2}\end{array}\right.$

Answer

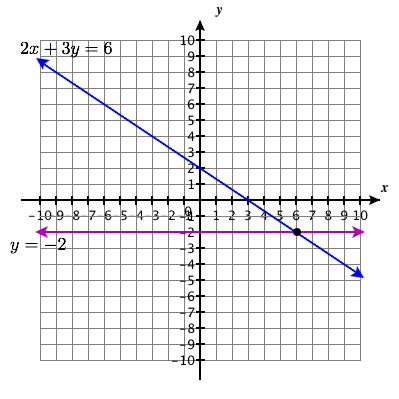
Solution Point: $(6,−2)$

Exercise $\PageIndex{32}$

$\left\{\begin{array}{l}{-2 x+y=2} \\ {y=4}\end{array}\right.$

Exercise $\PageIndex{33}$

$\left\{\begin{array}{l}{x-3 y=-3} \\ {y=2}\end{array}\right.$

Answer

Solution Point: $(3,2)$

Exercise $\PageIndex{34}$

$\left\{\begin{array}{l}{2 x-2 y=8} \\ {y=-3}\end{array}\right.$

Exercise $\PageIndex{35}$

$\left\{\begin{array}{l}{2 x-y=-1} \\ {x=1}\end{array}\right.$

Answer

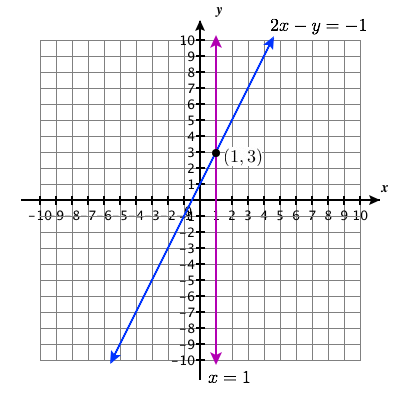
Solution Point: $(1,3)$

Exercise $\PageIndex{36}$

$\left\{\begin{array}{l}{x+2 y=2} \\ {x=-2}\end{array}\right.$

Exercise $\PageIndex{37}$

$\left\{\begin{array}{l}{x-3 y=-6} \\ {x=-3}\end{array}\right.$

Answer

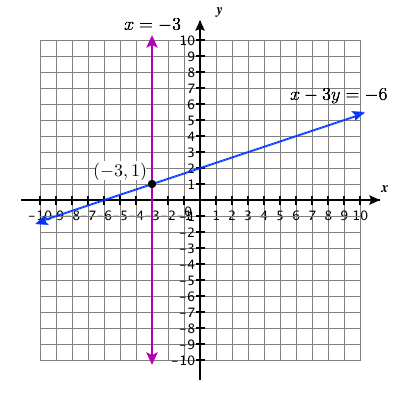
Solution Point: $(−3,1)$

Exercise $\PageIndex{38}$

$\left\{\begin{array}{l}{x+y=4} \\ {x=1}\end{array}\right.$

Exercise $\PageIndex{39}$

$\left\{\begin{array}{l}{4 x-3 y=8} \\ {8 x-6 y=14}\end{array}\right.$

Answer

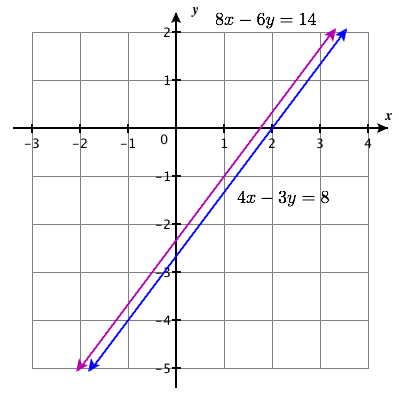
no solution

Exercise $\PageIndex{40}$

$\left\{\begin{array}{l}{x+3 y=4} \\ {-2 x-6 y=3}\end{array}\right.$

Exercise $\PageIndex{41}$

$\left\{\begin{array}{l}{-2 x+4 y=4} \\ {y=\frac{1}{2} x}\end{array}\right.$

Answer

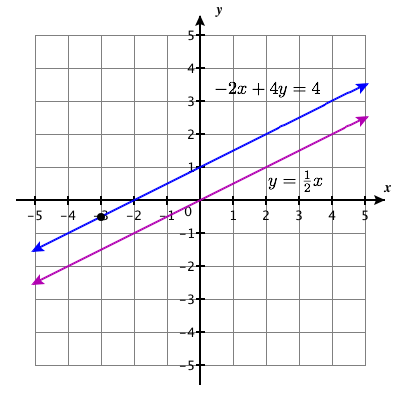
no solution

Exercise $\PageIndex{42}$

$\left\{\begin{array}{l}{3 x+5 y=10} \\ {y=-\frac{3}{5} x+1}\end{array}\right.$

Exercise $\PageIndex{43}$

$\left\{\begin{array}{l}{x=-3 y+4} \\ {2 x+6 y=8}\end{array}\right.$

Answer

no solution

Exercise $\PageIndex{44}$

$\left\{\begin{array}{l}{4 x=3 y+7} \\ {8 x-6 y=14}\end{array}\right.$

Exercise $\PageIndex{45}$

$\left\{\begin{array}{l}{2 x+y=6} \\ {-8 x-4 y=-24}\end{array}\right.$

Answer

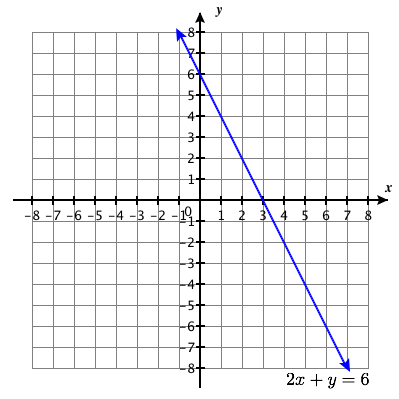
infinitely many solutions with solution set: $\big\{ (x,y) | 2 x+y=6\big\}$

Exercise $\PageIndex{46}$

$\left\{\begin{array}{l}{5 x+2 y=7} \\ {-10 x-4 y=-14}\end{array}\right.$

Exercise $\PageIndex{47}$

$\left\{\begin{array}{l}{x+3 y=-6} \\ {4 y=-\frac{4}{3} x-8}\end{array}\right.$

Answer

infinitely many solutions with solution set: $\big\{ (x,y) | x+3 y=-6\big\}$

Exercise $\PageIndex{48}$

$\left\{\begin{array}{l}{-x+2 y=-6} \\ {y=-\frac{1}{2} x-1}\end{array}\right.$

Exercise $\PageIndex{49}$

$\left\{\begin{array}{l}{-3 x+2 y=-2} \\ {y=-x+4}\end{array}\right.$

Answer

Solution Point: $(2,2)$

Exercise $\PageIndex{50}$

$\left\{\begin{array}{l}{-x+2 y=-2} \\ {y=-x-1}\end{array}\right.$

Determine the Number of Solutions of a Linear System Without graphing the following systems of equations, determine the number of solutions and then classify the system of equations.

Exercise $\PageIndex{51}$

$\left\{\begin{array}{l}{y=\frac{2}{3} x+1} \\ {-2 x+3 y=5}\end{array}\right.$

Answer

0 solutions

Exercise $\PageIndex{52}$

$\left\{\begin{array}{l}{y=\frac{1}{3} x+2} \\ {x-3 y=9}\end{array}\right.$

Exercise $\PageIndex{53}$

$\left\{\begin{array}{l}{y=-2 x+1} \\ {4 x+2 y=8}\end{array}\right.$

Answer

0 solutions

Exercise $\PageIndex{54}$

$\left\{\begin{array}{l}{y=3 x+4} \\ {9 x-3 y=18}\end{array}\right.$

Exercise $\PageIndex{55}$

$\left\{\begin{array}{l}{y=\frac{2}{3} x+1} \\ {2 x-3 y=7}\end{array}\right.$

Answer

0 solutions

Exercise $\PageIndex{56}$

$\left\{\begin{array}{l}{3 x+4 y=12} \\ {y=-3 x-1}\end{array}\right.$

Exercise $\PageIndex{57}$

$\left\{\begin{array}{l}{4 x+2 y=10} \\ {4 x-2 y=-6}\end{array}\right.$

Answer

consistent, 1 solution

Exercise $\PageIndex{58}$

$\left\{\begin{array}{l}{5 x+3 y=4} \\ {2 x-3 y=5}\end{array}\right.$

Exercise $\PageIndex{59}$

$\left\{\begin{array}{l}{y=-\frac{1}{2} x+5} \\ {x+2 y=10}\end{array}\right.$

Answer

infinitely many solutions

Exercise $\PageIndex{60}$

$\left\{\begin{array}{l}{y=x+1} \\ {-x+y=1}\end{array}\right.$

Exercise $\PageIndex{61}$

$\left\{\begin{array}{l}{y=2 x+3} \\ {2 x-y=-3}\end{array}\right.$

Answer

infinitely many solutions

Exercise $\PageIndex{62}$

$\left\{\begin{array}{l}{5 x-2 y=10} \\ {y=\frac{5}{2} x-5}\end{array}\right.$

Solve Applications of Systems of Equations by Graphing In the following exercises, solve.

Exercise $\PageIndex{63}$

Molly is making strawberry infused water. For each ounce of strawberry juice, she uses three times as many ounces of water. How many ounces of strawberry juice and how many ounces of water does she need to make 64 ounces of strawberry infused water?

Answer

Molly needs 16 ounces of strawberry juice and 48 ounces of water.

Exercise $\PageIndex{64}$

Jamal is making a snack mix that contains only pretzels and nuts. For every ounce of nuts, he will use 2 ounces of pretzels. How many ounces of pretzels and how many ounces of nuts does he need to make 45 ounces of snack mix?

Exercise $\PageIndex{65}$

Enrique is making a party mix that contains raisins and nuts. For each ounce of nuts, he uses twice the amount of raisins. How many ounces of nuts and how many ounces of raisins does he need to make 24 ounces of party mix?

Answer

Enrique needs 8 ounces of nuts and 16 ounces of water.

Exercise $\PageIndex{66}$

Owen is making lemonade from concentrate. The number of quarts of water he needs is 4 times the number of quarts of concentrate. How many quarts of water and how many quarts of concentrate does Owen need to make 100 quarts of lemonade?

Everyday Math

Exercise $\PageIndex{67}$

Leo is planning his spring flower garden. He wants to plant tulip and daffodil bulbs. He will plant 6 times as many daffodil bulbs as tulip bulbs. If he wants to plant 350 bulbs, how many tulip bulbs and how many daffodil bulbs should he plant?

Answer

Leo should plant 50 tulips and 300 daffodils.

Exercise $\PageIndex{68}$

A marketing company surveys 1,200 people. They surveyed twice as many females as males. How many males and females did they survey?

Writing Exercises

Exercise $\PageIndex{69}$

In a system of linear equations, the two equations have the same slope. Describe the possible solutions to the system.

Answer

Given that it is only known that the slopes of both linear equations are the same, there are either no solutions (the graphs of the equations are parallel) or infinitely many.

Exercise $\PageIndex{70}$

In a system of linear equations, the two equations have the same intercepts. Describe the possible solutions to the system.

Self Check

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

If most of your checks were:

…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.