5.3E: Exercises
- Last updated
- Jan 6, 2020
- Save as PDF
- Page ID
- 30524
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
Solve a System of Equations by Elimination
In the following exercises, solve the systems of equations by elimination.
Exercise 5.3E.1
{5x+2y=2−3x−y=0
Exercise 5.3E.2
{−3x+y=−9x−2y=−12
- Answer
-
(6,9)
Exercise 5.3E.3
{6x−5y=−12x+y=13
Exercise 5.3E.4
{3x−y=−74x+2y=−6
- Answer
-
(−2,1)
Exercise 5.3E.5
{x+y=−1x−y=−5
Exercise 5.3E.6
{x+y=−8x−y=−6
- Answer
-
(−7,−1)
Exercise 5.3E.7
{3x−2y=1−x+2y=9
Exercise 5.3E.8
{−7x+6y=−10x−6y=22
- Answer
-
(−2,−4)
Exercise 5.3E.9
{3x+2y=−3−x−2y=−19
Exercise 5.3E.10
{5x+2y=1−5x−4y=−7
- Answer
-
(−1,3)
Exercise 5.3E.11
{6x+4y=−4−6x−5y=8
Exercise 5.3E.12
{3x−4y=−11x−2y=−5
- Answer
-
(−1,2)
Exercise 5.3E.13
{5x−7y=29x+3y=−3
Exercise 5.3E.14
{6x−5y=−75−x−2y=−13
- Answer
-
(−5,9)
Exercise 5.3E.15
{−x+4y=83x+5y=10
Exercise 5.3E.16
{2x−5y=73x−y=17
- Answer
-
(6,1)
Exercise 5.3E.17
{5x−3y=−12x−y=2
Exercise 5.3E.18
{7x+y=−413x+3y=4
- Answer
-
(−2,10)
Exercise 5.3E.19
{−3x+5y=−132x+y=−26
Exercise 5.3E.20
{3x−5y=−95x+2y=16
- Answer
-
(2,3)
Exercise 5.3E.21
{4x−3y=32x+5y=−31
Exercise 5.3E.22
{4x+7y=14−2x+3y=32
- Answer
-
(−7,6)
Exercise 5.3E.23
{5x+2y=217x−4y=9
Exercise 5.3E.24
{3x+8y=−32x+5y=−3
- Answer
-
(−9,3)
Exercise 5.3E.25
{11x+9y=−57x+5y=−1
Exercise 5.3E.26
{3x+8y=675x+3y=60
Answer
-
(9,5)
Exercise 5.3E.27
{2x+9y=−43x+13y=−7
Exercise 5.3E.28
{13x−y=−3x+52y=2
- Answer
-
(−3,2)
Exercise 5.3E.29
{x+12y=3215x−15y=3
Exercise 5.3E.30
{x+13y=−112x−13y=−2
- Answer
-
(−2,3)
Exercise 5.3E.31
{13x−y=−323x+52y=3
Exercise 5.3E.32
{2x+y=36x+3y=9
- Answer
-
infinitely many solutions
Exercise 5.3E.33
{x−4y=−1−3x+12y=3
Exercise 5.3E.34
{−3x−y=86x+2y=−16
- Answer
-
infinitely many solutions
Exercise 5.3E.35
{4x+3y=220x+15y=10
Exercise 5.3E.36
{3x+2y=6−6x−4y=−12
- Answer
-
infinitely many solutions
Exercise 5.3E.37
{5x−8y=1210x−16y=20
Exercise 5.3E.38
{−11x+12y=60−22x+24y=90
- Answer
-
inconsistent, no solution
Exercise 5.3E.39
{7x−9y=16−21x+27y=−24
Exercise 5.3E.40
{5x−3y=15y=53x−2
- Answer
-
inconsistent, no solution
Exercise 5.3E.41
{2x+4y=7y=−12x−4
Solve Applications of Systems of Equations by Elimination
In the following exercises, translate to a system of equations and solve.
Exercise 5.3E.42
The sum of two numbers is 65. Their difference is 25. Find the numbers.
- Answer
-
The numbers are 20 and 45.
Exercise 5.3E.43
The sum of two numbers is 37. Their difference is 9. Find the numbers.
Exercise 5.3E.44
The sum of two numbers is −27. Their difference is −59. Find the numbers.
- Answer
-
The numbers are 16 and −43.
Exercise 5.3E.45
The sum of two numbers is −45. Their difference is −89. Find the numbers.
Exercise 5.3E.46
Andrea is buying some new shirts and sweaters. She is able to buy 3 shirts and 2 sweaters for $114 or she is able to buy 2 shirts and 4 sweaters for $164. How much does a shirt cost? How much does a sweater cost?
- Answer
-
A shirt costs $16 and a sweater costs $33.
Exercise 5.3E.47
Peter is buying office supplies. He is able to buy 3 packages of paper and 4 staplers for $40 or he is able to buy 5 packages of paper and 6 staplers for $62. How much does a package of paper cost? How much does a stapler cost?
Exercise 5.3E.48
The total amount of sodium in 2 hot dogs and 3 cups of cottage cheese is 4720 mg. The total amount of sodium in 5 hot dogs and 2 cups of cottage cheese is 6300 mg. How much sodium is in a hot dog? How much sodium is in a cup of cottage cheese?
- Answer
-
There are 860 mg in a hot dog. There are 1,000 mg in a cup of cottage cheese.
Exercise 5.3E.49
The total number of calories in 2 hot dogs and 3 cups of cottage cheese is 960 calories. The total number of calories in 5 hot dogs and 2 cups of cottage cheese is 1190 calories. How many calories are in a hot dog? How many calories are in a cup of cottage cheese?
Choose the Most Convenient Method to Solve a System of Linear Equations
In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.
Exercise 5.3E.50
- {8x−15y=−326x+3y=−5
- {x=4y−34x−2y=−6
- Answer
-
- elimination
- substitution
Exercise 5.3E.51
- {y=7x−53x−2y=16
- {12x−5y=−423x+7y=−15
Exercise 5.3E.52
- {y=4x+95x−2y=−21
- {9x−4y=243x+5y=−14
- Answer
-
- substitution
- elimination
Exercise 5.3E.53
- {14x−15y=−307x+2y=10
- {x=9y−112x−7y=−27
Everyday Math
Exercise 5.3E.54
In one hour Norris can row 3 miles upstream against the current. In the same amount of time he can row 5 miles downstream, with the current. Solve the system. {r−c=3r+c=5
- for r, his rowing speed in still water.
- Then solve for c, the speed of the river current.
- Answer
-
- r=4
- c=1
Exercise 5.3E.55
Josie wants to make 10 pounds of trail mix using nuts and raisins, and she wants the total cost of the trail mix to be $54. Nuts cost $6 per pound and raisins cost $3 per pound. Solve the system {n+r=106n+3r=54 to find n, the number of pounds of nuts, and rr, the number of pounds of raisins she should use.
Writing Exercises
Exercise 5.3E.56
Solve the system
{x+y=105x+8y=56
- by substitution
- by graphing
- Which method do you prefer? Why?
- Answer
-
- (8, 2)
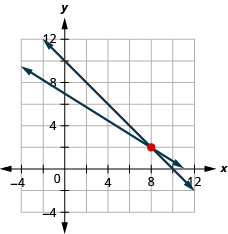
3. Answers will vary.
Exercise 5.3E.57
Solve the system {x+y=−12y=4−12x
- by substitution
- by graphing
- Which method do you prefer? Why?
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. What does this checklist tell you about your mastery of this section? What steps will you take to improve?


