5.4E: Exercises
- Page ID
- 30526
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Practice Makes Perfect
Translate to a System of Equations
In the following exercises, translate to a system of equations and solve the system.
The sum of two numbers is fifteen. One number is three less than the other. Find the numbers.
- Answer
-
The numbers are 6 and 9.
The sum of two numbers is twenty-five. One number is five less than the other. Find the numbers.
The sum of two numbers is negative thirty. One number is five times the other. Find the numbers.
- Answer
-
The numbers are −5 and −25.
The sum of two numbers is negative sixteen. One number is seven times the other. Find the numbers.
Twice a number plus three times a second number is twenty-two. Three times the first number plus four times the second is thirty-one. Find the numbers.
- Answer
-
The numbers are 5 and 4.
Six times a number plus twice a second number is four. Twice the first number plus four times the second number is eighteen. Find the numbers.
Three times a number plus three times a second number is fifteen. Four times the first plus twice the second number is fourteen. Find the numbers.
- Answer
-
The numbers are 2 and 3.
Twice a number plus three times a second number is negative one. The first number plus four times the second number is two. Find the numbers.
A married couple together earn $75,000. The husband earns $15,000 more than five times what his wife earns. What does the wife earn?
- Answer
-
$10,000
During two years in college, a student earned $9,500. The second year she earned $500 more than twice the amount she earned the first year. How much did she earn the first year?
Daniela invested a total of $50,000, some in a certificate of deposit (CD) and the remainder in bonds. The amount invested in bonds was $5000 more than twice the amount she put into the CD. How much did she invest in each account?
- Answer
-
She put $15,000 into a CD and $35,000 in bonds.
Jorge invested $28,000 into two accounts. The amount he put in his money market account was $2,000 less than twice what he put into a CD. How much did he invest in each account?
In her last two years in college, Marlene received $42,000 in loans. The first year she received a loan that was $6,000 less than three times the amount of the second year’s loan. What was the amount of her loan for each year?
- Answer
-
The amount of the first year’s loan was $30,000 and the amount of the second year’s loan was $12,000.
Jen and David owe $22,000 in loans for their two cars. The amount of the loan for Jen’s car is $2000 less than twice the amount of the loan for David’s car. How much is each car loan?
Solve Direct Translation Applications
In the following exercises, translate to a system of equations and solve.
Alyssa is twelve years older than her sister, Bethany. The sum of their ages is forty-four. Find their ages.
- Answer
-
Bethany is 16 years old and Alyssa is 28 years old.
Robert is 15 years older than his sister, Helen. The sum of their ages is sixty-three. Find their ages.
The age of Noelle’s dad is six less than three times Noelle’s age. The sum of their ages is seventy-four. Find their ages.
- Answer
-
Noelle is 20 years old and her dad is 54 years old.
The age of Mark’s dad is 4 less than twice Marks’s age. The sum of their ages is ninety-five. Find their ages.
Two containers of gasoline hold a total of fifty gallons. The big container can hold ten gallons less than twice the small container. How many gallons does each container hold?
- Answer
-
The small container holds 20 gallons and the large container holds 30 gallons.
June needs 48 gallons of punch for a party and has two different coolers to carry it in. The bigger cooler is five times as large as the smaller cooler. How many gallons can each cooler hold?
Shelly spent 10 minutes jogging and 20 minutes cycling and burned 300 calories. The next day, Shelly swapped times, doing 20 minutes of jogging and 10 minutes of cycling and burned the same number of calories. How many calories were burned for each minute of jogging and how many for each minute of cycling?
- Answer
-
There were 10 calories burned jogging and 10 calories burned cycling.
Drew burned 1800 calories Friday playing one hour of basketball and canoeing for two hours. Saturday he spent two hours playing basketball and three hours canoeing and burned 3200 calories. How many calories did he burn per hour when playing basketball?
Troy and Lisa were shopping for school supplies. Each purchased different quantities of the same notebook and thumb drive. Troy bought four notebooks and five thumb drives for $116. Lisa bought two notebooks and three thumb dives for $68. Find the cost of each notebook and each thumb drive.
- Answer
-
Notebooks are $4 and thumb drives are $20.
Nancy bought seven pounds of oranges and three pounds of bananas for $17. Her husband later bought three pounds of oranges and six pounds of bananas for $12. What was the cost per pound of the oranges and the bananas?
Solve Geometry Applications In the following exercises, translate to a system of equations and solve.
The difference of two complementary angles is 30 degrees. Find the measures of the angles.
- Answer
-
The measures are 60 degrees and 30 degrees.
The difference of two complementary angles is 68 degrees. Find the measures of the angles.
The difference of two supplementary angles is 70 degrees. Find the measures of the angles.
- Answer
-
The measures are 125 degrees and 55 degrees.
The difference of two supplementary angles is 24 degrees. Find the measure of the angles.
The difference of two supplementary angles is 8 degrees. Find the measures of the angles.
- Answer
-
94 degrees and 86 degrees
The difference of two supplementary angles is 88 degrees. Find the measures of the angles.
The difference of two complementary angles is 55 degrees. Find the measures of the angles.
- Answer
-
72.5 degrees and 17.5 degrees
The difference of two complementary angles is 17 degrees. Find the measures of the angles.
Two angles are supplementary. The measure of the larger angle is four more than three times the measure of the smaller angle. Find the measures of both angles.
- Answer
-
The measures are 44 degrees and 136 degrees.
Two angles are supplementary. The measure of the larger angle is five less than four times the measure of the smaller angle. Find the measures of both angles.
Two angles are complementary. The measure of the larger angle is twelve less than twice the measure of the smaller angle. Find the measures of both angles.
- Answer
-
The measures are 34 degrees and 56 degrees.
Two angles are complementary. The measure of the larger angle is ten more than four times the measure of the smaller angle. Find the measures of both angles.
Wayne is hanging a string of lights 45 feet long around the three sides of his rectangular patio, which is adjacent to his house. The length of his patio, the side along the house, is five feet longer than twice its width. Find the length and width of the patio.
- Answer
-
The width is 10 feet and the length is 25 feet.
Darrin is hanging 200 feet of Christmas garland on the three sides of fencing that enclose his rectangular front yard. The length, the side along the house, is five feet less than three times the width. Find the length and width of the fencing.
A frame around a rectangular family portrait has a perimeter of 60 inches. The length is fifteen less than twice the width. Find the length and width of the frame.
- Answer
-
The width is 15 feet and the length is 15 feet.
The perimeter of a rectangular toddler play area is 100 feet. The length is ten more than three times the width. Find the length and width of the play area.
Solve Uniform Motion Applications In the following exercises, translate to a system of equations and solve.
Sarah left Minneapolis heading east on the interstate at a speed of 60 mph. Her sister followed her on the same route, leaving two hours later and driving at a rate of 70 mph. How long will it take for Sarah’s sister to catch up to Sarah?
- Answer
-
It took Sarah’s sister 12 hours.
College roommates John and David were driving home to the same town for the holidays. John drove 55 mph, and David, who left an hour later, drove 60 mph. How long will it take for David to catch up to John?
At the end of spring break, Lucy left the beach and drove back towards home, driving at a rate of 40 mph. Lucy’s friend left the beach for home 30 minutes (half an hour) later, and drove 50 mph. How long did it take Lucy’s friend to catch up to Lucy?
- Answer
-
It took Lucy’s friend 2 hours.
Felecia left her home to visit her daughter driving 45 mph. Her husband waited for the dog sitter to arrive and left home twenty minutes (1/3 hour) later. He drove 55 mph to catch up to Felecia. How long before he reaches her?
The Jones family took a 12 mile canoe ride down the Indian River in two hours. After lunch, the return trip back up the river took three hours. Find the rate of the canoe in still water and the rate of the current.
- Answer
-
The canoe rate is 5 mph and the current rate is 1 mph.
A motor boat travels 60 miles down a river in three hours but takes five hours to return upstream. Find the rate of the boat in still water and the rate of the current.
A motor boat traveled 18 miles down a river in two hours but going back upstream, it took 4.5 hours due to the current. Find the rate of the motor boat in still water and the rate of the current.
- Answer
-
The boat rate is 6.5 mph and the current rate is 2.5 mph.
A river cruise boat sailed 80 miles down the Mississippi River for four hours. It took five hours to return. Find the rate of the cruise boat in still water and the rate of the current.
A small jet can fly 1,072 miles in 4 hours with a tailwind but only 848 miles in 4 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
- Answer
-
The jet rate is 240 mph and the wind speed is 28 mph.
A small jet can fly 1,435 miles in 5 hours with a tailwind but only 1215 miles in 5 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
A commercial jet can fly 868 miles in 2 hours with a tailwind but only 792 miles in 2 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
- Answer
-
The jet rate is 415 mph and the wind speed is 19 mph.
A commercial jet can fly 1,320 miles in 3 hours with a tailwind but only 1,170 miles in 3 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
Everyday Math
At a school concert, 425 tickets were sold. Student tickets cost $5 each and adult tickets cost $8 each. The total receipts for the concert were $2,851. Solve the system
\(\left\{\begin{array}{l}{s+a=425} \\ {5 s+8 a=2,851}\end{array}\right.\)
to find s, the number of student tickets and aa, the number of adult tickets.
- Answer
-
s=183,a=242
The first graders at one school went on a field trip to the zoo. The total number of children and adults who went on the field trip was 115. The number of adults was \(\frac{1}{4}\) the number of children. Solve the system
\(\left\{\begin{array}{l}{c+a=115} \\ {a=\frac{1}{4} c}\end{array}\right.\)
to find c, the number of children and aa, the number of adults.
Writing Exercises
Write an application problem similar to Example using the ages of two of your friends or family members. Then translate to a system of equations and solve it.
- Answer
-
Answers will vary.
Write a uniform motion problem similar to Example that relates to where you live with your friends or family members. Then translate to a system of equations and solve it.
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?
More Practice: Number Problems
Set up a linear system and solve.
1. The sum of two integers is \(45\). The larger integer is \(3\) less than twice the smaller. Find the two integers.
2. The sum of two integers is \(126\). The larger is \(18\) less than \(5\) times the smaller. Find the two integers.
3. The sum of two integers is \(41\). When \(3\) times the smaller is subtracted from the larger the result is \(17\). Find the two integers.
4. The sum of two integers is \(46\). When the larger is subtracted from twice the smaller the result is \(2\). Find the two integers.
5. The difference of two integers is \(11\). When twice the larger is subtracted from \(3\) times the smaller, the result is \(3\). Find the integers.
6. The difference of two integers is \(6\). The sum of twice the smaller and the larger is \(72\). Find the integers.
7. The sum of \(3\) times a larger integer and \(2\) times a smaller is \(15\). When \(3\) times the smaller integer is subtracted from twice the larger, the result is \(23\). Find the integers.
8. The sum of twice a larger integer and \(3\) times a smaller is \(10\). When the \(4\) times the smaller integer is added to the larger, the result is \(0\). Find the integers.
9. The difference of twice a smaller integer and \(7\) times a larger is \(4\). When \(5\) times the larger integer is subtracted from \(3\) times the smaller, the result is \(−5\). Find the integers.
10. The difference of a smaller integer and twice a larger is \(0\). When \(3\) times the larger integer is subtracted from \(2\) times the smaller, the result is \(−5\). Find the integers.
- Answer
-
1. The integers are \(16\) and \(29\).
3. The integers are \(6\) and \(35\).
5. The integers are \(25\) and \(36\).
7. The integers are \(−3\) and \(7\).
9. The integers are \(−5\) and \(−2\).
More Practice: Geometry Problems
1. The length of a rectangle is \(5\) more than twice its width. If the perimeter measures \(46\) meters, then find the dimensions of the rectangle.
2. The width of a rectangle is \(2\) centimeters less than one-half its length. If the perimeter measures \(62\) centimeters, then find the dimensions of the rectangle.
3. A partitioned rectangular pen next to a river is constructed with a total \(136\) feet of fencing (see illustration).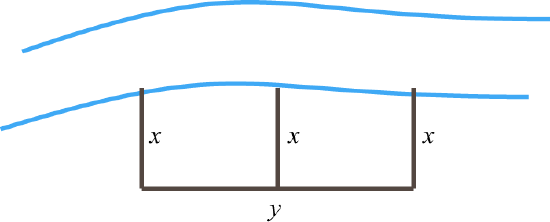 
If the outer fencing measures \(114\) feet, then find the dimensions of the pen.
4. A partitioned rectangular pen is constructed with a total \(168\) feet of fencing (see illustration). 
the perimeter measures \(138\) feet, then find the dimensions of the pen.
Add exercises text here.
- Answer
-
1. Length: \(17\) meters; width: \(6\) meters 3. Width: \(22\) feet; length: \(70\) feet.
More Practice: Distance Problems
Set up a linear system and solve.
- The two legs of a \(432\)-mile trip took \(8\) hours. The average speed for the first leg of the trip was \(52\) miles per hour and the average speed for the second leg of the trip was \(60\) miles per hour. How long did each leg of the trip take?
- Jerry took two buses on the \(265\)-mile trip from Los Angeles to Las Vegas. The first bus averaged \(55\) miles per hour and the second bus was able to average \(50\) miles per hour. If the total trip took \(5\) hours, then how long was spent in each bus?
- An executive was able to average \(48\) miles per hour to the airport in her car and then board an airplane that averaged \(210\) miles per hour. The \(549\)-mile business trip took \(3\) hours. How long did it take her to drive to the airport?
- Joe spends \(1\) hour each morning exercising by jogging and then cycling for a total of \(15\) miles. He is able to average \(6\) miles per hour jogging and \(18\) miles per hour cycling. How long does he spend jogging each morning?
- Swimming with the current Jack can swim \(2.5\) miles in \(\frac{1}{2}\) hour. Swimming back, against the same current, he can only swim \(2\) miles in the same amount of time. How fast is the current?
- A light aircraft flying with the wind can travel \(180\) miles in \(1 \frac{1}{2}\) hours. The aircraft can fly the same distance against the wind in \(2\) hours. Find the speed of the wind.
- A light airplane flying with the wind can travel \(600\) miles in \(4\) hours. On the return trip, against the wind, it will take \(5\) hours. What are the speeds of the airplane and of the wind?
- A boat can travel \(15\) miles with the current downstream in \(1 \frac{1}{4}\) hours. Returning upstream against the current, the boat can only travel \(8 \frac{3}{4}\) miles in the same amount of time. Find the speed of the current.
- Mary jogged the trail from her car to the cabin at the rate of \(6\) miles per hour. She then walked back to her car at a rate of \(4\) miles per hour. If the entire trip took \(1\) hour, then how long did it take her to walk back to her car?
- A jogger can sustain an average running rate of \(8\) miles per hour to his destination and \(6\) miles an hour on the return trip. Find the total distance the jogger ran if the total time running was \(1 \frac{3}{4}\) hour.
- Two trains leave the station traveling in opposite directions. One train is \(12\) miles per hour faster than the other and in \(3\) hours they are \(300\) miles apart. Determine the average speed of each train.
- Two trains leave the station traveling in opposite directions. One train is \(8\) miles per hour faster than the other and in \(2 \frac{1}{2}\) hours they are \(230\) miles apart. Determine the average speed of each train.
- Answer
-
1. The first leg of the trip took \(6\) hours and the second leg took \(2\) hours.
3. It took her \(\frac{1}{2}\) hour to drive to the airport.
5. \(0.5\) miles per hour.
7. Airplane: \(135\) miles per hour; wind: \(15\) miles per hour
9. \(\frac{3}{5}\) hour
11. One train averaged \(44\) miles per hour and the other averaged \(56\) miles per hour.