7.6E: Exercises
- Last updated
- Jan 6, 2020
- Save as PDF
- Page ID
- 30560
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
Use the Zero Product Property
In the following exercises, solve.
Exercise 1
- Answer
-
Exercise 2
Exercise 3
- Answer
-
Exercise 4
Exercise 5
- Answer
-
Exercise 6
Exercise 7
- Answer
-
Exercise 8
Exercise 9
- Answer
-
Exercise 10
Solve Quadratic Equations by Factoring
In the following exercises, solve.
Exercise 11
- Answer
-
Exercise 12
Exercise 13
- Answer
-
Exercise 14
Exercise 15
- Answer
-
Exercise 16
Exercise 17
- Answer
-
Exercise 18
Exercise 19
- Answer
-
Exercise 20
Exercise 21
- Answer
-
Exercise 22
Exercise 23
- Answer
-
Exercise 24
Exercise 25
- Answer
-
Exercise 26
Exercise 27
- Answer
-
Exercise 28
Solve Applications Modeled by Quadratic Equations
In the following exercises, solve.
Exercise 29
The product of two consecutive integers is 56. Find the integers.
- Answer
-
7 and 8; −8 and −7
Exercise 30
The product of two consecutive integers is 42. Find the integers.
Exercise 31
The area of a rectangular carpet is 28 square feet. The length is three feet more than the width. Find the length and the width of the carpet.
- Answer
-
4 feet and 7 feet
Exercise 32
A rectangular retaining wall has area 15 square feet. The height of the wall is two feet less than its length. Find the height and the length of the wall.
Exercise 33
A pennant is shaped like a right triangle, with hypotenuse 10 feet. The length of one side of the pennant is two feet longer than the length of the other side. Find the length of the two sides of the pennant.
- Answer
-
6 feet and 8 feet
Exercise 34
A reflecting pool is shaped like a right triangle, with one leg along the wall of a building. The hypotenuse is 9 feet longer than the side along the building. The third side is 7 feet longer than the side along the building. Find the lengths of all three sides of the reflecting pool.
Mixed Practice
In the following exercises, solve.
Exercise 35
(x+8)(x−3)=0
- Answer
-
Exercise 36
(3y−5)(y+7)=0
Exercise 37
- Answer
-
Exercise 38
Exercise 39
- Answer
-
Exercise 40
Exercise 41
- Answer
-
Exercise 42
Exercise 43
The product of two consecutive integers is 110. Find the integers.
- Answer
-
10 and 11; −11 and −10
Exercise 44
The length of one leg of a right triangle is three more than the other leg. If the hypotenuse is 15, find the lengths of the two legs.
Everyday Math
Exercise 45
Area of a patio If each side of a square patio is increased by 4 feet, the area of the patio would be 196 square feet. Solve the equation (s+4)2=196(s+4)2=196 for s to find the length of a side of the patio.
- Answer
-
10 feet
Exercise 46
Watermelon drop A watermelon is dropped from the tenth story of a building. Solve the equation −16t2+144=0−16t2+144=0 for tt to find the number of seconds it takes the watermelon to reach the ground.
Writing Exercises
Exercise 47
Explain how you solve a quadratic equation. How many answers do you expect to get for a quadratic equation?
- Answer
-
Answers may vary for the explanation. You should expect no more than 2 solutions for a quadratic equation. Often it has two solutions, but sometimes, it can have one repeated solution or even no solution.
Exercise 48
Give an example of a quadratic equation that has a GCF and none of the solutions to the equation is zero.
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
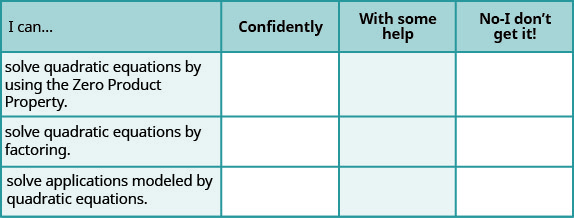
b. Overall, after looking at the checklist, do you think you are well-prepared for the next section? Why or why not?


