9.6: Graph Quadratic Functions Using Properties

Last updated
Save as PDF

Page ID: 30917

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Learning Objectives

By the end of this section, you will be able to:

Recognize the graph of a quadratic function
Find the axis of symmetry and vertex of a parabola
Find the intercepts of a parabola
Graph quadratic functions using properties
Solve maximum and minimum applications

Before you get started, take this readiness quiz.

Graph the function $f(x)=x^{2}$ by plotting points.
If you missed this problem, review Example 3.54.
Solve: $2 x^{2}+3 x-2=0$.
If you missed this problem, review Example 6.45.
Evaluate $-\frac{b}{2 a}$ when $a=3$ and $b=-6$.
If you missed this problem, review Example 1.21.

Recognize the Graph of a Quadratic Function

Previously we very briefly looked at the function $f(x)=x^{2}$, which we called the square function. It was one of the first non-linear functions we looked at. Now we will graph functions of the form $f(x)=a x^{2}+b x+c$ if $a \neq 0$. We call this kind of function a quadratic function.

Definition $\PageIndex{1}$

A quadratic function, where $a, b$, and $c$ are real numbers and $a≠0$, is a function of the form

$f(x)=a x^{2}+b x+c$

We graphed the quadratic function $f(x)=x^{2}$ by plotting points.

This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 4 to 4. The y-axis of the plane runs from negative 2 to 6. The parabola has a vertex at (0, 0) and also passes through the points (-2, 4), (-1, 1), (1, 1), and (2, 4). To the right of the graph is a table of values with 3 columns. The first row is a header row and labels each column, â€œxâ€, â€œf of x equals x squaredâ€, and â€œthe order pair x, f of x.â€ In row 2, x equals negative 3, f of x equals x squared is 9 and the ordered pair x, f of x is the ordered pair negative 3, 9. In row 3, x equals negative 2, f of x equals x squared is 4 and the ordered pair x, f of x is the ordered pair negative 2, 4. In row 4, x equals negative 1, f of x equals x squared is 1 and the ordered pair x, f of x is the ordered pair negative 1, 1. In row 5, x equals 0, f of x equals x squared is 0 and the ordered pair x, f of x is the ordered pair 0, 0. In row 6, x equals 1, f of x equals x squared is 1 and the ordered pair x, f of x is the ordered pair 1, 1. In row 7, x equals 2, f of x equals x squared is 4 and the ordered pair x, f of x is the ordered pair 2, 4. In row 8, x equals 3, f of x equals x squared is 9 and the ordered pair x, f of x is the ordered pair 3, 9. — Figure 9.6.1

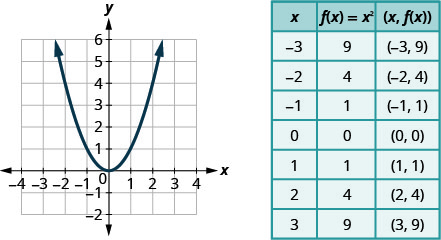
Every quadratic function has a graph that looks like this. We call this figure a parabola. Let’s practice graphing a parabola by plotting a few points.

Example $\PageIndex{1}$

Graph: $f(x)=x^{2}-1$.

Solution:

We will graph the function by plotting points.

Choose integer values for $x$, substitute them into the equation and simplify to find $f(x)$. Record the values of the ordered pairs in the chart.	$.$
Plot the points, and then connect them with a smooth curve. The result will be the graph of the function $f(x)=x^{2}-1$.	$.$

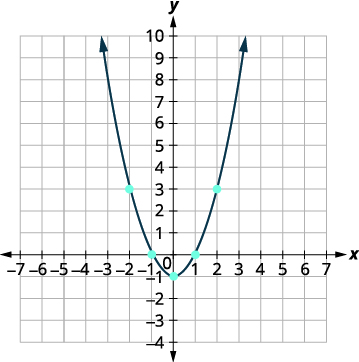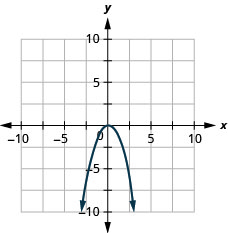
Exercise $\PageIndex{1}$

Graph $f(x)=-x^{2}$.

Answer: $This figure shows an downward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (0, 0).$

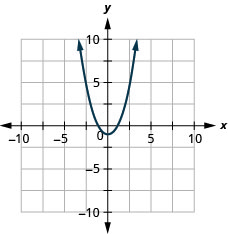
Exercise $\PageIndex{2}$

Graph $f(x)=x^{2}+1$.

Answer: $This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (0, âˆ’1).$

All graphs of quadratic functions of the form $f(x)=a x^{2}+b x+c$ are parabolas that open upward or downward. See Figure 9.6.6

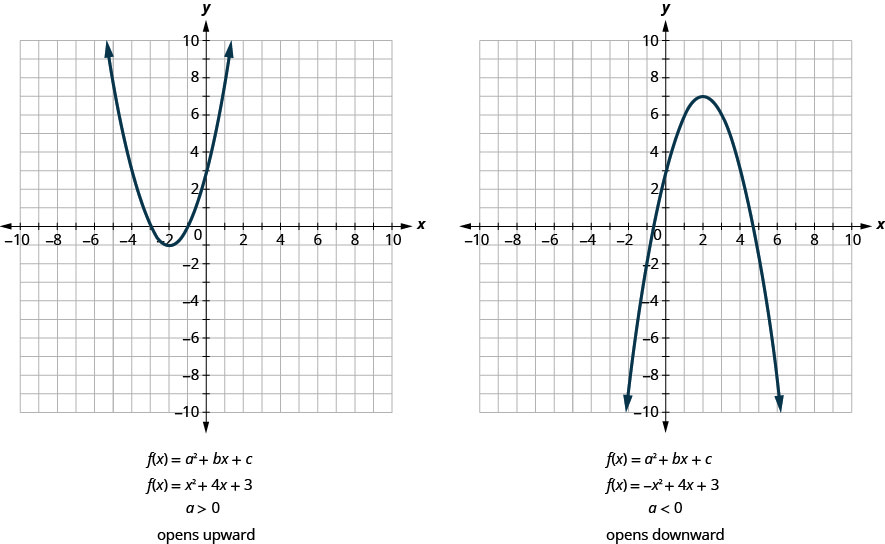
This image shows 2 graphs side-by-side. The graph on the left shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (negative 2, negative 1) and passes through the points (negative 4, 3) and (0, 3). The general form for the equation of this graph is f of x equals a x squared plus b x plus c. The equation of this parabola is x squared plus 4 x plus 3. The leading coefficient, a, is greater than 0, so this parabola opens upward.The graph on the right shows an downward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (2, 7) and passes through the points (0, 3) and (4, 3). The general form for the equation of this graph is f of x equals a x squared plus b x plus c. The equation of this parabola is negative x squared plus 4 x plus 3. The leading coefficient, a, is less than 0, so this parabola opens downward.

Notice that the only difference in the two functions is the negative sign before the quadratic term ($x^{2}$ in the equation of the graph in Figure 9.6.6). When the quadratic term, is positive, the parabola opens upward, and when the quadratic term is negative, the parabola opens downward.

Definition $\PageIndex{2}$

Parabola Orientation

For the graph of the quadratic function $f(x)=a x^{2}+b x+c$, if

$This images shows a bulleted list. The first bullet notes that, if a is greater than 0, then the parabola opens upward and shows an image of an upward-opening parabola. The second bullet notes that, if a is less than 0, then the parabola opens downward and shows an image of a downward-opening parabola.$

Example $\PageIndex{2}$

Determine whether each parabola opens upward or downward:

$f(x)=-3 x^{2}+2 x-4$
$f(x)=6 x^{2}+7 x-9$

Solution:

a. Find the value of $a$.

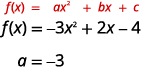
Since the $a$ is negative, the parabola will open downward.

b. Find the value of $a$.

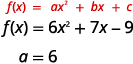
Since the $a$ is positive, the parabola will open upward.

Exercise $\PageIndex{3}$

Determine whether the graph of each function is a parabola that opens upward or downward:

$f(x)=2 x^{2}+5 x-2$
$f(x)=-3 x^{2}-4 x+7$

Answer

up
down

Exercise $\PageIndex{4}$

Determine whether the graph of each function is a parabola that opens upward or downward:

$f(x)=-2 x^{2}-2 x-3$
$f(x)=5 x^{2}-2 x-1$

Answer

down
up

Find the Axis of Symmetry and Vertex of a Parabola

Look again at Figure 9.6.10. Do you see that we could fold each parabola in half and then one side would lie on top of the other? The ‘fold line’ is a line of symmetry. We call it the axis of symmetry of the parabola.

We show the same two graphs again with the axis of symmetry.

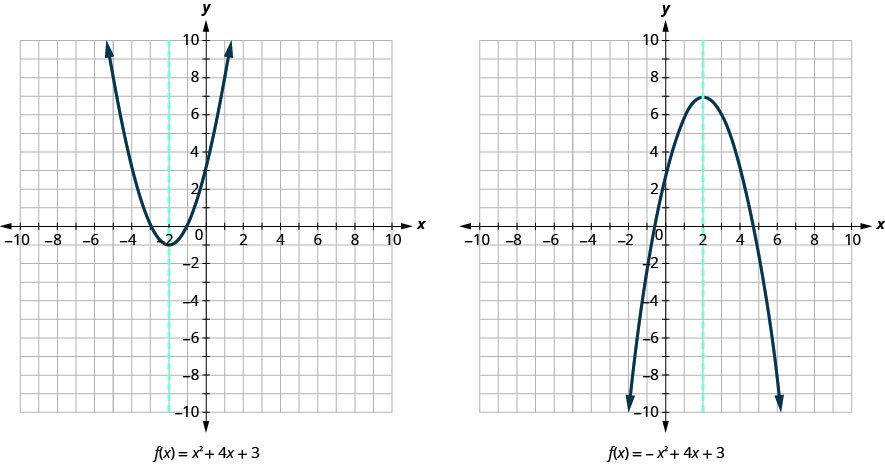
This image shows 2 graphs side-by-side. The graph on the left shows an upward-opening parabola and a dashed vertical line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (negative 2, negative 1) and passes through the points (negative 4, 3) and (0, 3). The equation of this parabola is x squared plus 4 x plus 3. The vertical line passes through the point (negative 2, 0) and has the equation x equals negative 2. The graph on the right shows an downward-opening parabola and a dashed vertical line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (2, 7) and passes through the points (0, 3) and (4, 3). The equation of this parabola is negative x squared plus 4 x plus 3. The vertical line passes through the point (2, 0) and has the equation x equals 2.

The equation of the axis of symmetry can be derived by using the Quadratic Formula. We will omit the derivation here and proceed directly to using the result. The equation of the axis of symmetry of the graph of $f(x)=a x^{2}+b x+c$ is $x=-\frac{b}{2 a}$.

So to find the equation of symmetry of each of the parabolas we graphed above, we will substitute into the formula $x=-\frac{b}{2 a}$.

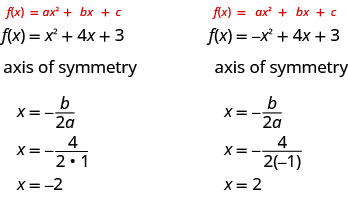
Compare the function f of x equals x squared plus 4 x plus 3 to the standard form of a quadratic function, f of x equals a x squared plus b x plus c. The axis of symmetry is the line x equals negative b divided by the product 2 a. Substituting for b and a yields x equals negative 4 divided by the product 2 times 1. The axis of symmetry equals negative 2. Next, compare the function f of x equals negative x squared plus 4 x plus 3 to the standard form of a quadratic function, f of x equals a x squared plus b x plus c. The axis of symmetry is the line x equals negative b divided by the product 2 a. Substituting for b and a yields x equals negative 4 divided by the product 2 times negative 1. The axis of symmetry equals 2.

Notice that these are the equations of the dashed blue lines on the graphs.

The point on the parabola that is the lowest (parabola opens up), or the highest (parabola opens down), lies on the axis of symmetry. This point is called the vertex of the parabola.

We can easily find the coordinates of the vertex, because we know it is on the axis of symmetry. This means its
$x$-coordinate is $-\frac{b}{2 a}$. To find the $y$-coordinate of the vertex we substitute the value of the $x$-coordinate into the quadratic function.

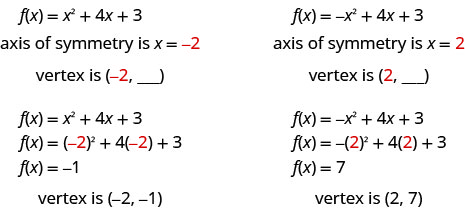
For the function f of x equals x squared plus 4 x plus 3, the axis of symmetry is x equals negative 2. The vertex is the point on the parabola with x-coordinate negative 2. Substitute x equals negative 2 into the function f of x equals x squared plus 4 x plus 3. F of x equals the square of negative 2 plus 4 times negative 2 plus 3, so f of x equals negative 1. The vertex is the point (negative 2, negative 1). For the function f of x equals negative x squared plus 4 x plus 3, the axis of symmetry is x equals 2. The vertex is the point on the parabola with x-coordinate 2. Substitute x equals 2 into the function f of x equals x squared plus 4 x plus 3. F of x equals 2 squared plus 4 times 2 plus 3, so f of x equals 7. The vertex is the point (2, 7).

Axis of Symmetry and Vertex of a Parabola

The graph of the function $f(x)=a x^{2}+b x+c$ is a parabola where:

the axis of symmetry is the vertical line $x=-\frac{b}{2 a}$.
the vertex is a point on the axis of symmetry, so its $x$-coordinate is $-\frac{b}{2 a}$
the $y$-coordinate of the vertex is found by substituting $x=-\frac{b}{2 a}$ into the quadratic equation.

Example $\PageIndex{3}$

For the graph of $f(x)=3 x^{2}-6 x+2$ find:

the axis of symmetry
the vertex

Solution:

	$.$
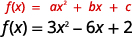The axis of symmetry is the vertical line $x=-\frac{b}{2 a}$.
Substitute the values $a,b$ into the equation.	$x=-\frac{-6}{2 \cdot 3}$
Simplify.	$x=1$
	The axis of symmetry is the line $x=1$.

	$f(x)=3 x^{2}-6 x+2$
The vertex is a point on the line of symmetry, so its $x$-coordinate will be $x=1$. Find $f(1)$.	$.$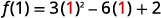
Simplify.	$.$
The result is the $y$-coordinate.	$f(1)=-1$
	The vertex is $(1,-1)$.

Exercise $\PageIndex{5}$

For the graph of $f(x)=2 x^{2}-8 x+1$ find:

the axis of symmetry
the vertex

Answer

$x=2$
$(2,-7)$

Exercise $\PageIndex{6}$

For the graph of $f(x)=2 x^{2}-4 x-3$ find:

the axis of symmetry
the vertex

Answer

$x=1$
$(1,-5)$

Find the Intercepts of a Parabola

When we graphed linear equations, we often used the $x$- and $y$-intercepts to help us graph the lines. Finding the coordinates of the intercepts will help us to graph parabolas, too.

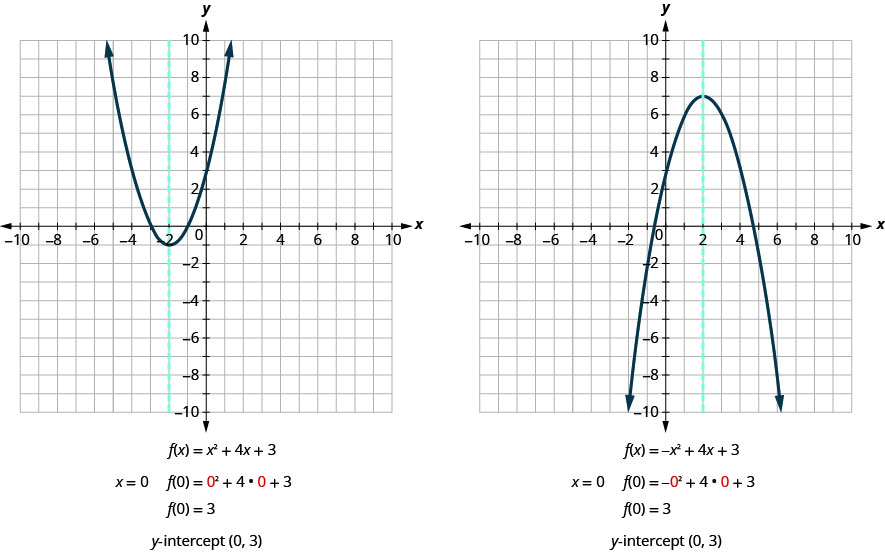
Remember, at the $y$-intercept the value of $x$ is zero. So to find the $y$-intercept, we substitute $x=0$ into the function.

Let’s find the $y$-intercepts of the two parabolas shown in Figure 9.6.20.

An $x$-intercept results when the value of $f(x)$ is zero. To find an $x$-intercept, we let $f(x)=0$. In other words, we will need to solve the equation $0=a x^{2}+b x+c$ for $x$.

$\begin{aligned} f(x) &=a x^{2}+b x+c \\ 0 &=a x^{2}+b x+c \end{aligned}$

Solving quadratic equations like this is exactly what we have done earlier in this chapter!

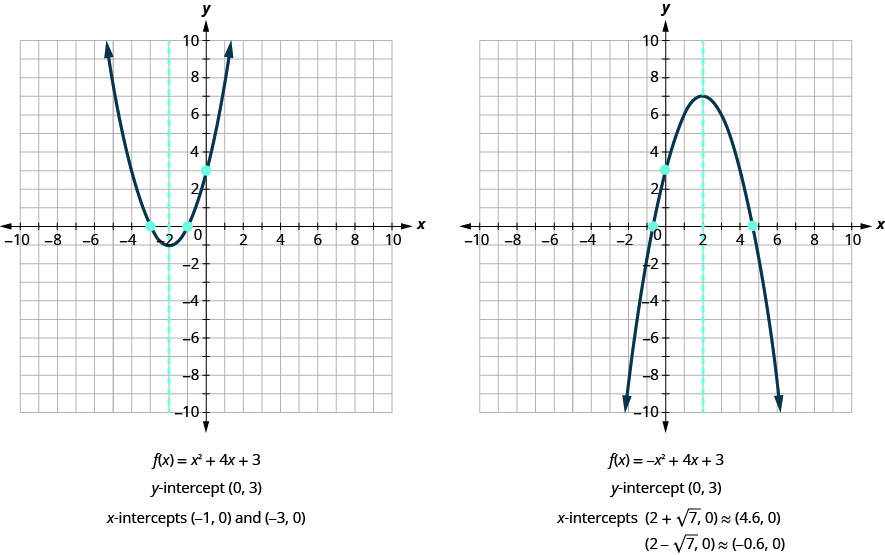
We can now find the $x$-intercepts of the two parabolas we looked at. First we will find the $x$-intercepts of the parabola whose function is $f(x)=x^{2}+4 x+3$.

	$f(x)=x^{2}+4 x+3$
Let $f(x)=0$.	$\color{red}0\color{black}=x^{2}+4 x+3$
Factor.	$0=(x+1)(x+3)$
Use the Zero Product Property.	$x+1=0 \quad x+3=0$
Solve.	$x=-1 \quad x=-3$
	The $x$-intercepts are $(-1,0)$ and $(-3,0)$.

Now we will find the $x$-intercepts of the parabola whose function is $f(x)=-x^{2}+4 x+3$.

	$f(x)=-x^{2}+4 x+3$
Let $f(x)=0$.	$\color{red}0 \color{black}=-x^{2}+4 x+3$
This quadratic does not factor, so we use the Quadratic Formula.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
$a=-1, b=4, c=3$	$x=\frac{-4 \pm \sqrt{4^{2}-4(-1)(3)}}{2(-1)}$
Simplify.	$x=\frac{-4 \pm \sqrt{28}}{-2}$
	$x=\frac{-4 \pm 2 \sqrt{7}}{-2}$
	$x=\frac{-2(2 \pm \sqrt{7})}{-2}$
	$x=2 \pm \sqrt{7}$
	The $x$-intercepts are $(2+\sqrt{7}, 0)$ and $(2-\sqrt{7}, 0)$.

We will use the decimal approximations of the $x$-intercepts, so that we can locate these points on the graph,

$(2+\sqrt{7}, 0) \approx(4.6,0) \quad(2-\sqrt{7}, 0) \approx(-0.6,0)$

Do these results agree with our graphs? See Figure 9.6.34

This image shows 2 graphs side-by-side. The graph on the left shows the upward-opening parabola defined by the function f of x equals x squared plus 4 x plus 3 and a dashed vertical line, x equals negative 2, graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (negative 2, negative 1). The y-intercept is (0, 3) and the x-intercepts are (negative 1, 0) and (negative 3, 0). The graph on the right shows the downward-opening parabola defined by the function f of x equals negative x squared plus 4 x plus 3 and a dashed vertical line, x equals 2, graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (2, 7). The y-intercept is (0, 3) and the x-intercepts are (2 plus square root 7, 0), approximately (4.6, 0) and (2 minus square root, 0), approximately (negative 0.6, 0).

Find the Intercepts of a Parabola

To find the intercepts of a parabola whose function is $f(x)=a x^{2}+b x+c$:

$y$-intercept

Let $x=0$ and solve for $f(x)$.

$x$-intercepts

Let $f(x)=0$ and solve for $x$

Example $\PageIndex{4}$

Find the intercepts of the parabola whose function is $f(x)=x^{2}-2 x-8$.

Solution:

To find the $y$-intercept, let $x=0$ and solve for $f(x)$.	$f(x)=x^{2}-2 x-8$
	$f(0)=\color{red}0\color{black}^{2}-2 \cdot \color{red}0 \color{black}-8$
	$f(0)=-8$
	When $x=0$, then $f(0)=-8$. The $y$-intercept is the point $(0,-8)$.
To find the $x$-intercept, let $f(x)=0$ and solve for $x$.	$f(x)=x^{2}-2 x-8$
	$0=x^{2}-2 x-8$
Solve by factoring.	$0=(x-4)(x+2)$
	$0=x-4 \quad 0=x+2$
	$4=x \quad-2=x$
	When $f(x)=0$, then $x=4$ or $x=-2$. The $x$-intercepts are the points $(4,0)$ and $(-2,0)$.

Exercise $\PageIndex{7}$

Find the intercepts of the parabola whose function is $f(x)=x^{2}+2 x-8$.

Answer: $y$ -intercept: $(0,-8) x$ -intercepts $(-4,0),(2,0)$

Exercise $\PageIndex{8}$

Find the intercepts of the parabola whose function is $f(x)=x^{2}-4 x-12$.

Answer: $y$ -intercept: $(0,-12) x$ -intercepts $(-2,0),(6,0)$

In this chapter, we have been solving quadratic equations of the form $a x^{2}+b x+c=0$. We solved for $x$ and the results were the solutions to the equation.

We are now looking at quadratic functions of the form $f(x)=a x^{2}+b x+c$. The graphs of these functions are parabolas. The $x$-intercepts of the parabolas occur where $f(x)=0$.

For example:

Quadratic equation

$\begin{aligned}x^{2}-2 x-15 & =0\quad \text{Let}\:f(x)=0 \\ (x-5)(x+3) &=0 \\ x-5=0\:\:x+3 & =0 \\ x=5\:\:\:x&=-3\end{aligned}$

Quadratic function

$\begin{aligned} f(x) &=x^{2}-2 x-15 \\ 0 &=x^{2}-2 x-15 \\ 0 &=(x-5)(x+3) \\ x-5 &=0 \quad x+3=0 \\ x &=5 \quad x=-3 \\(5,0) & \text { and }(-3,0) \\& x\text { -intercepts } \end{aligned}$

The solutions of the quadratic function are the $x$ values of the $x$-intercepts.

Earlier, we saw that quadratic equations have $2, 1$, or $0$ solutions. The graphs below show examples of parabolas for these three cases. Since the solutions of the functions give the $x$-intercepts of the graphs, the number of $x$-intercepts is the same as the number of solutions.

Previously, we used the discriminant to determine the number of solutions of a quadratic function of the form $a x^{2}+b x+c=0$. Now we can use the discriminant to tell us how many $x$-intercepts there are on the graph.

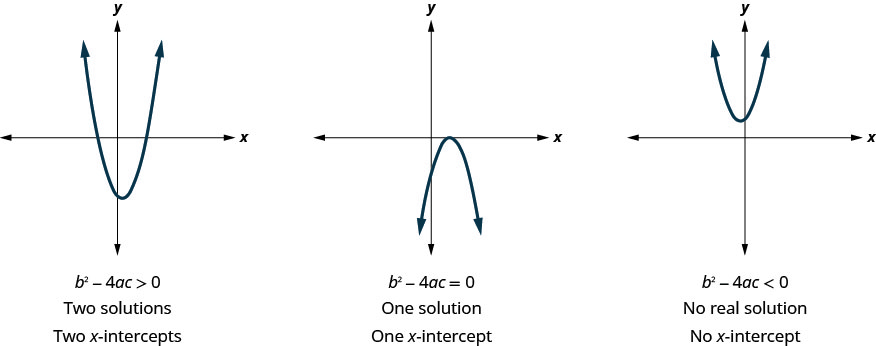
This image shows three graphs side-by-side. The graph on the left shows an upward-opening parabola graphed on the x y-coordinate plane. The vertex of the parabola lies below the x-axis and the parabola crosses the x-axis at two different points. If b squared minus 4 a c is greater than 0, then the quadratic equation a x squared plus b x plus c equals 0 has two solutions, and the graph of the parabola has 2 x-intercepts. The graph in the middle shows a downward-opening parabola graphed on the x y-coordinate plane. The vertex of the parabola lies on the x-axis, the only point of intersection between the parabola and the x-axis. If b squared minus 4 a c equals 0, then the quadratic equation a x squared plus b x plus c equals 0 has one solution, and the graph of the parabola has 1 x-intercept. The graph on the right shows an upward-opening parabola graphed on the x y-coordinate plane. The vertex of the parabola lies above the x-axis and the parabola does not cross the x-axis. If b squared minus 4 a c is less than 0, then the quadratic equation a x squared plus b x plus c equals 0 has no solutions, and the graph of the parabola has no x-intercepts.

Before you to find the values of the $x$-intercepts, you may want to evaluate the discriminant so you know how many solutions to expect.

Example $\PageIndex{5}$

Find the intercepts of the parabola for the function $f(x)=5 x^{2}+x+4$.

Solution:

	$.$
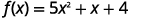To find the $y$-intercept, let $x=0$ and solve for $f(x)$.	$.$
	$.$
	When $x=0$, then $f(0)=4$. The $y$-intercept is the point $(0,4)$.
To find the $x$-intercept, let $f(x)=0$ and solve for $x$.	$.$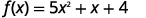
	$.$
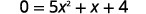Find the value of the discriminant to predict the number of solutions which is also the number of $x$-intercepts.
$\begin{array}{c}{b^{2}-4 a c} \\ {1^{2}-4 \cdot 5 \cdot 4} \\ {1-80} \\ {-79}\end{array}$
	Since the value of the discriminant is negative, there is no real solution to the equation. There are no $x$-intercepts.

Exercise $\PageIndex{9}$

Find the intercepts of the parabola whose function is $f(x)=3 x^{2}+4 x+4$.

Answer: $y$-intercept: $(0,4)$ no $x$-intercept

Exercise $\PageIndex{10}$

Find the intercepts of the parabola whose function is $f(x)=x^{2}-4 x-5$

Answer: $y$-intercept: $(0,-5)$ $x$-intercepts $(-1,0),(5,0)$

Graph Quadratic Functions Using Properties

Now we have all the pieces we need in order to graph a quadratic function. We just need to put them together. In the next example we will see how to do this.

Example $\PageIndex{6}$ How to Graph a Quadratic Function Using Properties

Graph $f(x)=x^{2}-6x+8$ by using its properties.

Solution:

Step 1: Determine whether the parabola opens upward or downward.	Look $a$ in the equation $f(x)=x^{2}-6x+8$ Since $a$ is positive, the parabola opens upward.	$f(x)=x^{2}-6x+8$ $\color{red}{a=1, b=-6, c=8}$ The parabola opens upward.
Step 2: Find the axis of symmetry.	$f(x)=x^{2}-6x+8$ The axis of symmetry is the line $x=-\frac{b}{2 a}$.	Axis of Symmetry $x=-\frac{b}{2 a}$ $x=-\frac{(-6)}{2 \cdot 1}$ $x=3$ The axis of symmetry is the line $x=3$.
Step 3: Find the vertex.	The vertex is on the axis of symmetry. Substitute $x=3$ into the function.	Vertex $f(x)=x^{2}-6x+8$ $f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8$ $f(3)=-1$ The vertex is $(3,-1)$.
Step 4: Find the $y$-intercept. Find the point symmetric to the $y$-intercept across the axis of symmetry.	We find $f(0)$. We use the axis of symmetry to find a point symmetric to the $y$-intercept. The $y$-intercept is $3$ units left of the axis of symmetry, $x=3$. A point $3$ units to the right of the axis of symmetry has $x=6$.	$y$-intercept $f(x)=x^{2}-6 x+8$ $f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8$ $f(0)=8$ The $y$-intercept is $(0,8)$. Point symmetric to $y$-intercept: The point is $(6,8)$.
Step 5: Find the $x$-intercepts. Find additional points if needed.	We solve $f(x)=0$. We can solve this quadratic equation by factoring.	$x$-intercepts $f(x)=x^{2}-6 x+8$ $\color{red}{0}\color{black}{=}x^{2}-6x+8$ $\color{red}{0}\color{black}{=}(x-2)(x-4)$ $x=2 or x=4$ The $x$-intercepts are $(2,0)$ and $(4,0)$.
Step 6: Graph the parabola.	We graph the vertex, intercepts, and the point symmetric to the $y$-intercept. We connect these $5$ points to sketch the parabola.	$Screenshot (1).png$

Exercise $\PageIndex{11}$

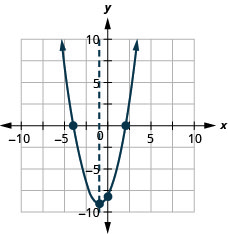
Graph $f(x)=x^{2}+2x-8$ by using its properties.

Answer: $This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The axis of symmetry, x equals negative 1, is graphed as a dashed line. The parabola has a vertex at (negative 1, negative 9). The y-intercept of the parabola is the point (0, negative 8). The x-intercepts of the parabola are the points (negative 4, 0) and (4, 0).$

Exercise $\PageIndex{12}$

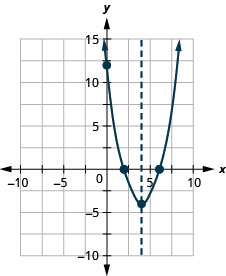
Graph $f(x)=x^{2}-8x+12$ by using its properties.

Answer

We list the steps to take in order to graph a quadratic function here.

To Graph a Quadratic Function Using Properties

Determine whether the parabola opens upward or downward.
Find the equation of the axis of symmetry.
Find the vertex.
Find the $y$-intercept. Find the point symmetric to the $y$-intercept across the axis of symmetry.
Find the $x$-intercepts. Find additional points if needed.
Graph the parabola.

We were able to find the $x$-intercepts in the last example by factoring. We find the $x$-intercepts in the next example by factoring, too.

Example $\PageIndex{7}$

Graph $f(x)=x^{2}+6 x-9$ by using its properties.

Solution:

	$.$
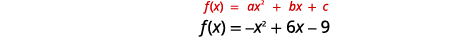Since $a$ is $-1$, the parabola opens downward.
	$.$
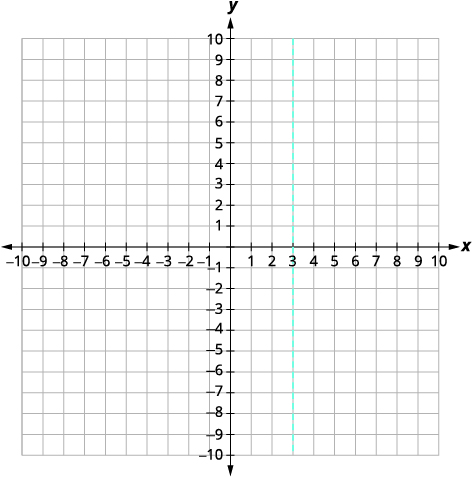
To find the equation of the axis of symmetry, use $x=-\frac{b}{2 a}$.	$x=-\frac{b}{2 a}$
	$x=-\frac{6}{2(-1)}$
	$x=3$
	The axis of symmetry is $x=3$. The vertex is on the line $x=3$.
	$.$
Find $f(3)$.	$f(x)=-x^{2}+6 x-9$
	$.$
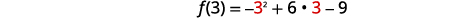	$f(3)=-9+18-9$
	$f(3)=0$
	The vertex is $(3,0)$.
	$.$
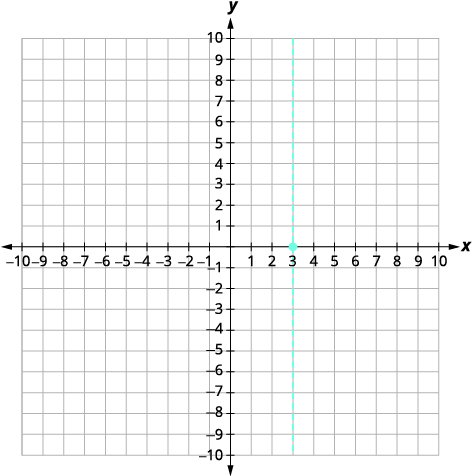The $y$-intercept occurs when $x=0$. Find $f(0)$.	$f(x)=-x^{2}+6 x-9$
Substitute $x=0$.	$.$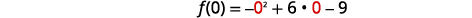
Simplify.	$f(0)=-9$
The point $(0,-9)$ is three units to the left of the line of symmetry. The point three units to the right of the line of symmetry is $(6,-9)$.	$.$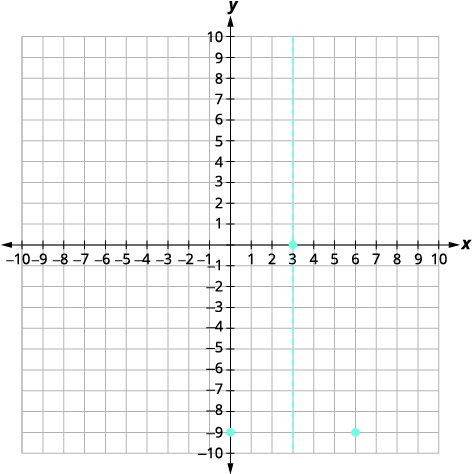
	Point symmetric to the $y$-intercept is $(6,-9)$
The $x$-intercept occurs when $f(x)=0$.	$.$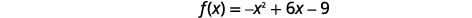
Find $f(x)=0$.	$.$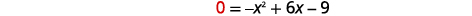
Factor the GCF.	$.$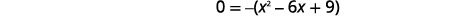
Factor the trinomial.	$.$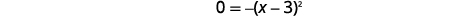
Solve for $x$.	$.$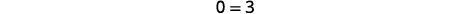
Connect the points to graph the parabola.	$.$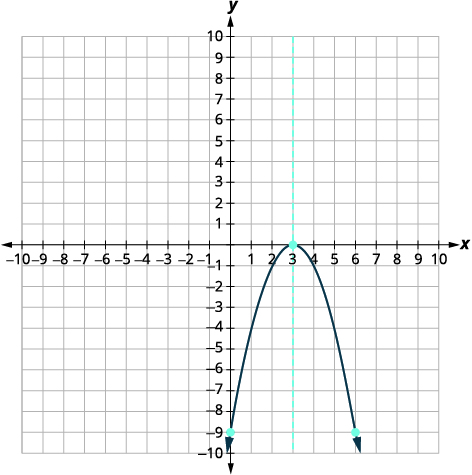

Exercise $\PageIndex{13}$

Graph $f(x)=3 x^{2}+12 x-12$ by using its properties.

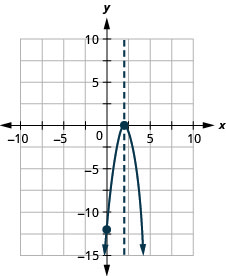
Answer: $This figure shows a downward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 15 to 10. The parabola has a vertex at (2, 0). The y-intercept (0, negative 12) is plotted as well as the axis of symmetry, x equals 2.$

Exercise $\PageIndex{14}$

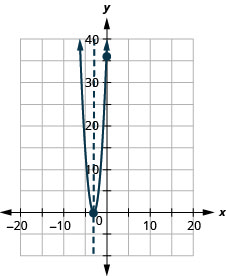
Graph $f(x)=4 x^{2}+24 x+36$ by using its properties.

Answer: $This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 30 to 20. The y-axis of the plane runs from negative 10 to 40. The parabola has a vertex at (negative 3, 0). The y-intercept (0, 36) is plotted as well as the axis of symmetry, x equals negative 3.$

For the graph of $f(x)=-x^{2}+6 x-9$, the vertex and the $x$-intercept were the same point. Remember how the discriminant determines the number of solutions of a quadratic equation? The discriminant of the equation $0=-x^{2}+6x-9$ is $0$, so there is only one solution. That means there is only one $x$-intercept, and it is the vertex of the parabola.

How many $x$-intercepts would you expect to see on the graph of $f(x)=x^{2}+4 x+5$?

Example $\PageIndex{8}$

Graph $f(x)=x^{2}+4 x+5$ by using its properties.

Solution:

	$.$
Since $a$ is $-1$, the parabola opens downward.
	$.$
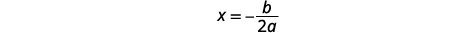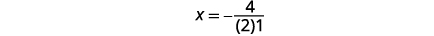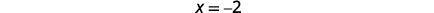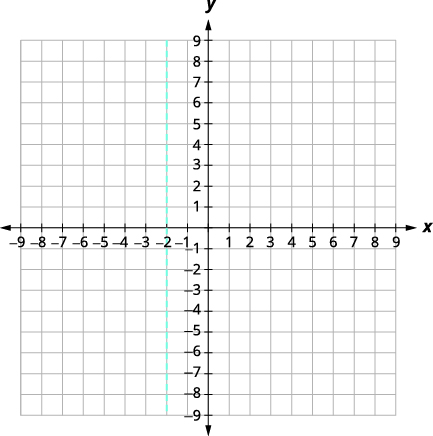
To find the equation of the axis of symmetry, use $x=-\frac{b}{2 a}$.	$.$

	$.$
	The equation of the axis of symmetry is \(x=-2).
	$.$
The vertex is on the line $x=-2$.
Find $f(x)$ when $x=-2$.	$.$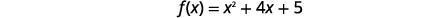
	$.$
	$.$

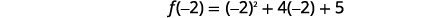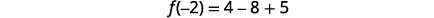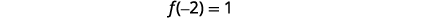	The vertex is $(-2,1)$.

The $y$-intercept occurs when $x=0$.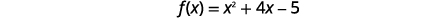
Find $f(0)$.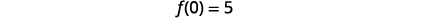
Simplify.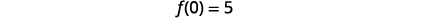
	The $y$-intercept is $(0,5)$.
The point $(-4,5)$ is two units to the left of the line of symmetry. The point to units to the right of the line of symmetry is \((0,5)\.	$.$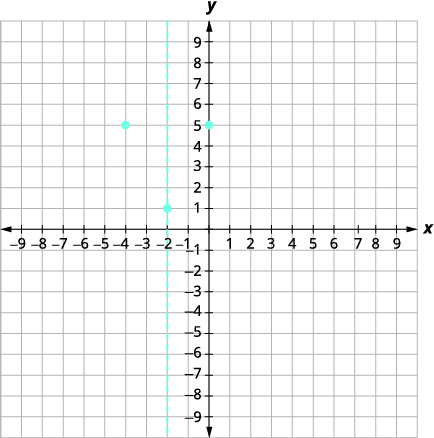
	Point symmetric to the $y$-intercept is $(-4,5)$.
The $x$-intercept occurs when $f(x)=0$.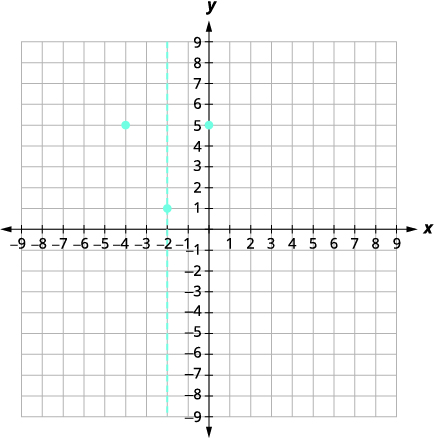
Find $f(x)=0$.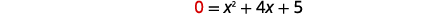
Test the discriminant.

	$.$
	$.$
	$.$
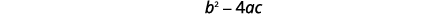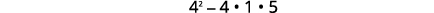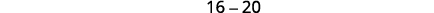Since the value of the discriminant is negative, there is no real solution and so no $x$-intercept.
Connect the points to graph the parabola. You may want to choose two more points for greater accuracy.	$.$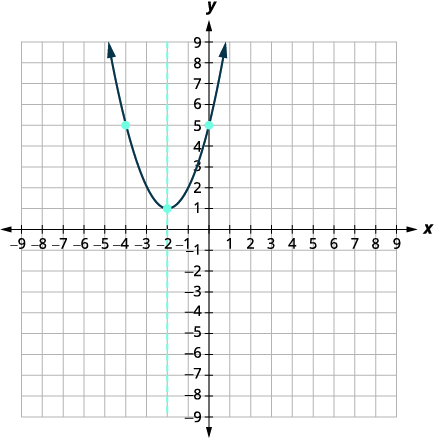

Exercise $\PageIndex{15}$

Graph $f(x)=x^{2}-2 x+3$ by using its properties.

Answer

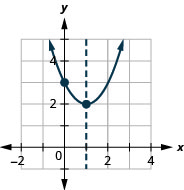
Exercise $\PageIndex{16}$

Graph $f(x)=-3x^{2}-6 x-4$ by using its properties.

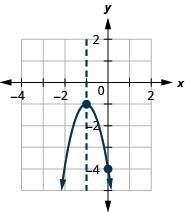
Answer: $This figure shows a downward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 4 to 2. The y-axis of the plane runs from negative 5 to 1. The parabola has a vertex at (negative 1, negative 2). The y-intercept (0, negative 4) is plotted as is the line of symmetry, x equals negative 1.$

Finding the $y$-intercept by finding $f(0)$ is easy, isn't it? Sometimes we need to use the Quadratic Formula to find the $x$-intercepts.

Example $\PageIndex{9}$

Graph $f(x)=2 x^{2}-4 x-3$ by using its properties.

Solution:

	$.$
Since $a$ is $2$, the parabola opens upward.	$.$
To find the equation of the axis of symmetry, use $x=-\frac{b}{2 a}$.	$x=-\frac{b}{2 a}$
	$x=-\frac{-4}{2 \cdot 2}$
	$x=1$
	The equation of the axis of symmetry is $x=1$.
The vertex is on the line $x=1$.	$f(x)=2 x^{2}-4 x-3$
Find $f(1)$.	$.$
	$f(1)=2-4-3$
	\(\f(1)=-5)
	The vertex is $(1,-5)$.
The $y$-intercept occurs when $x=0$.	$f(x)=2 x^{2}-4 x-3$
Find $f(0)$.
Simplify.	$f(0)=-3$
	The $y$-intercept is $(0,-3)$.
The point $(0,-3)$ is one unit to the left of the line of symmetry.	Point symmetric to the $y$-intercept is $(2,-3)$
The point one unit to the right of the line of symmetry is $(2,3)$.
The $x$-intercept occurs when $y=0$.	$f(x)=2 x^{2}-4 x-3$
Find $f(x)=0$.
Use the Quadratic Formula.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
Substitute in the values of $a,b$ and $c$.	$x=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(2)(3)}}{2(2)}$
Simplify.	$x=\frac{-4 \pm \sqrt{16+24}}{4}$
Simplify inside the radical.	$x=\frac{4 \pm \sqrt{40}}{4}$
Simplify the radical.	$x=\frac{4 \pm 2 \sqrt{10}}{4}$
Factor the GCF.	$x=\frac{2(2 \pm \sqrt{10})}{4}$
Remove common factors.	$x=\frac{2 \pm \sqrt{10}}{2}$
Write as two equations.	$x=\frac{2+\sqrt{10}}{2}, \quad x=\frac{2-\sqrt{10}}{2}$
Approximate the values.	$x \approx 2.5, \quad x \approx-0.6$
	The approximate values of the $x$-intercepts are $(2.5,0)$ and $(-0.6,0)$.
Graph the parabola using the points found.	$.$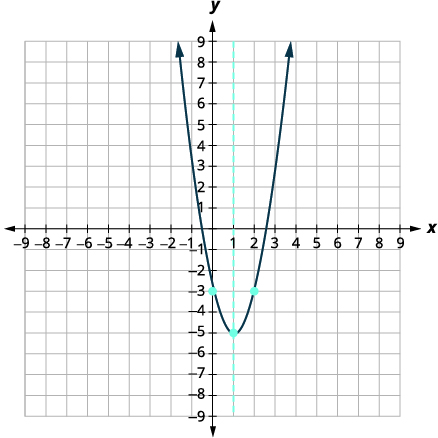

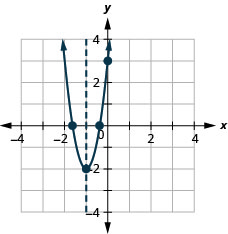
Exercise $\PageIndex{17}$

Graph $f(x)=5 x^{2}+10 x+3$ by using its properties.

Answer: $This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 4 to 4. The y-axis of the plane runs from negative 4 to 4. The axis of symmetry, x equals negative 1, is graphed as a dashed line. The parabola has a vertex at (negative 1, negative 2). The y-intercept of the parabola is the point (0, 3). The x-intercepts of the parabola are approximately (negative 1.6, 0) and (negative 0.4, 0).$

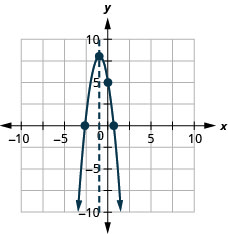
Exercise $\PageIndex{18}$

Graph $f(x)=-3 x^{2}-6 x+5$ by using its properties.

Answer: $This figure shows a downward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The axis of symmetry, x equals negative 1, is graphed as a dashed line. The parabola has a vertex at (negative 1, 8). The y-intercept of the parabola is the point (0, 5). The x-intercepts of the parabola are approximately (negative 2.6, 0) and (0.6, 0).$

Solve Maximum and Minimum Applications

Knowing that the vertex of a parabola is the lowest or highest point of the parabola gives us an easy way to determine the minimum or maximum value of a quadratic function. The y-coordinate of the vertex is the minimum value of a parabola that opens upward. It is the maximum value of a parabola that opens downward. See Figure 9.6.124.

This figure shows 2 graphs side-by-side. The left graph shows a downward opening parabola plotted in the x y-plane. An arrow points to the vertex with the label maximum. The right graph shows an upward opening parabola plotted in the x y-plane. An arrow points to the vertex with the label minimum. — Figure 9.6.124

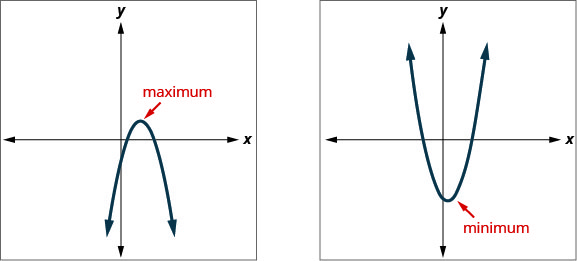
Minimum or Maximum Values of a Quadratic Function

The y-coordinate of the vertex of the graph of a quadratic function is the

minimum value of the quadratic equation if the parabola opens upward.
maximum value of the quadratic equation if the parabola opens downward.

Example $\PageIndex{10}$

Find the minimum or maximum value of the quadratic function $f(x)=x^{2}+2 x-8$.

Solution:

	$f(x)=x^{2}+2 x-8$
Since $a$ is positive, the parabola opens upward. The quadratic equation has a minimum.
Find the equation of the axis of symmetry.	$x=-\frac{b}{2 a}$
	$x=-\frac{2}{2 \times 1}$
	$x=-1$
	The equation of the axis of symmetry is $x=-1$.
The vertex is on the line $x=-1$.	$f(x)=x^{2}+2 x-8$
Find $f(-1)$.	$.$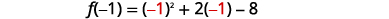
	$f(-1)=1-2-8$
	$f(-1)=-9$
	The vertex is $(-1,-9)$.
Since the parabola has a minimum, the $y$-coordinate of the vertex is the minimum $y$-value of the quadratic equation. The minimum value of the quadratic is $-9$ and it occurs when $x=-1$.
	$.$

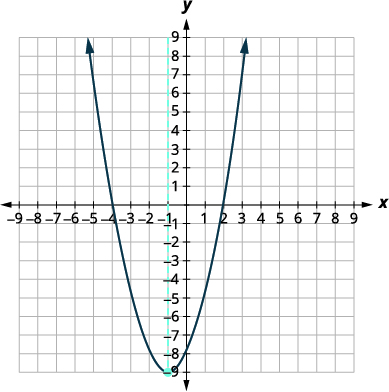Show the graph to verify the result.

Exercise $\PageIndex{19}$

Find the maximum or minimum value of the quadratic function $f(x)=x^{2}-8 x+12$.

Answer: The minimum value of the quadratic function is $−4$ and it occurs when $x=4$.

Exercise $\PageIndex{20}$

Find the maximum or minimum value of the quadratic function $f(x)=-4 x^{2}+16 x-11$.

Answer: The maximum value of the quadratic function is $5$ and it occurs when $x=2$.

We have used the formula

$h(t)=-16 t^{2}+v_{0} t+h_{0}$

to calculate the height in feet, $h$, of an object shot upwards into the air with initial velocity, $v_{0}$, after $t$ seconds .

This formula is a quadratic function, so its graph is a parabola. By solving for the coordinates of the vertex $(t,h)$, we can find how long it will take the object to reach its maximum height. Then we can calculate the maximum height.

Example $\PageIndex{11}$

The quadratic equation $h(t)=-16 t^{2}+176 t+4$ models the height of a volleyball hit straight upwards with velocity $176$ feet per second from a height of $4$ feet.

How many seconds will it take the volleyball to reach its maximum height?
Find the maximum height of the volleyball.

Solution:

$h(t)=-16 t^{2}+176 t+4$

Since $a$ is negative, the parabola opens downward. The quadratic function has a maximum.

a. Find the equation of the axis of symmetry.

$\begin{array}{l}{t=-\frac{b}{2 a}} \\ {t=-\frac{176}{2(-16)}} \\ {t=5.5}\end{array}$

The equation of the axis of symmetry is $t=5.5$.

The vertex is on the line $t=5.5$.

The maximum occurs when $t=5.5$ seconds.

b. Find $h(5.5)$.

$\begin{array}{l}{h(t)=-16 t^{2}+176 t+4} \\ {h(t)=-16(5.5)^{2}+176(5.5)+4}\end{array}$

Use a calculator to simplify.

$h(t)=488$

The vertex is $(5.5,488)$.

Since the parabola has a maximum, the $h$-coordinate of the vertex is the maximum value of the quadratic function.

The maximum value of the quadratic is $488$ feet and it occurs when $t=5.5$ seconds.

After $5.5$ seconds, the volleyball will reach its maximum height of $488$ feet.

Exercise $\PageIndex{21}$

Solve, rounding answers to the nearest tenth.

The quadratic function $h(t)=-16 t^{2}+128 t+32$ is used to find the height of a stone thrown upward from a height of $32$ feet at a rate of $128$ ft/sec. How long will it take for the stone to reach its maximum height? What is the maximum height?

Answer: It will take $4$ seconds for the stone to reach its maximum height of $288$ feet.

Exercise $\PageIndex{22}$

A path of a toy rocket thrown upward from the ground at a rate of $208$ ft/sec is modeled by the quadratic function of $h(t)=-16 t^{2}+208 t$. When will the rocket reach its maximum height? What will be the maximum height?

Answer: It will take $6.5$ seconds for the rocket to reach its maximum height of $676$ feet.

Key Concepts

Parabola Orientation
- For the graph of the quadratic function $f(x)=a x^{2}+b x+c$, if
  - $a>0$, the parabola opens upward.
  - $a<0$, the parabola opens downward.
Axis of Symmetry and Vertex of a Parabola The graph of the function $f(x)=a x^{2}+b x+c$ is a parabola where:
- the axis of symmetry is the vertical line $x=-\frac{b}{2 a}$.
- the vertex is a point on the axis of symmetry, so its $x$-coordinate is $-\frac{b}{2 a}$.
- the $y$-coordinate of the vertex is found by substituting $x=-\frac{b}{2 a}$ into the quadratic equation.
Find the Intercepts of a Parabola
- To find the intercepts of a parabola whose function is $f(x)=a x^{2}+b x+c$:
  - $y$-intercept
    - Let $x=0$ and solve for $f(x)$.
  - $x$-intercepts
    - Let $f(x)=0$ and solve for $x$.
How to graph a quadratic function using properties.
1. Determine whether the parabola opens upward or downward.
2. Find the equation of the axis of symmetry.
3. Find the vertex.
4. Find the $y$-intercept. Find the point symmetric to the y-intercept across the axis of symmetry.
5. Find the $x$-intercepts. Find additional points if needed.
6. Graph the parabola.
Minimum or Maximum Values of a Quadratic Equation
- The $y$-coordinate of the vertex of the graph of a quadratic equation is the
- minimum value of the quadratic equation if the parabola opens upward.
- maximum value of the quadratic equation if the parabola opens downward.

Glossary

quadratic function: A quadratic function, where $a, b$, and $c$ are real numbers and $a≠0$, is a function of the form $f(x)=ax^{2}+bx+c$.

	$.$
The axis of symmetry is the vertical line \(x=-\frac{b}{2 a}\).
Substitute the values \(a,b\) into the equation.	\(x=-\frac{-6}{2 \cdot 3}\)
Simplify.	\(x=1\)
	The axis of symmetry is the line \(x=1\).

	\(f(x)=3 x^{2}-6 x+2\)
The vertex is a point on the line of symmetry, so its \(x\)-coordinate will be \(x=1\). Find \(f(1)\).	$.$
Simplify.	$.$
The result is the \(y\)-coordinate.	\(f(1)=-1\)
	The vertex is \((1,-1)\).

	\(f(x)=x^{2}+4 x+3\)
Let \(f(x)=0\).	\(\color{red}0\color{black}=x^{2}+4 x+3\)
Factor.	\(0=(x+1)(x+3)\)
Use the Zero Product Property.	\(x+1=0 \quad x+3=0\)
Solve.	\(x=-1 \quad x=-3\)
	The \(x\)-intercepts are \((-1,0)\) and \((-3,0)\).

	\(f(x)=-x^{2}+4 x+3\)
Let \(f(x)=0\).	\(\color{red}0 \color{black}=-x^{2}+4 x+3\)
This quadratic does not factor, so we use the Quadratic Formula.	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
\(a=-1, b=4, c=3\)	\(x=\frac{-4 \pm \sqrt{4^{2}-4(-1)(3)}}{2(-1)}\)
Simplify.	\(x=\frac{-4 \pm \sqrt{28}}{-2}\)
	\(x=\frac{-4 \pm 2 \sqrt{7}}{-2}\)
	\(x=\frac{-2(2 \pm \sqrt{7})}{-2}\)
	\(x=2 \pm \sqrt{7}\)
	The \(x\)-intercepts are \((2+\sqrt{7}, 0)\) and \((2-\sqrt{7}, 0)\).

To find the \(y\)-intercept, let \(x=0\) and solve for \(f(x)\).	\(f(x)=x^{2}-2 x-8\)
	\(f(0)=\color{red}0\color{black}^{2}-2 \cdot \color{red}0 \color{black}-8\)
	\(f(0)=-8\)
	When \(x=0\), then \(f(0)=-8\). The \(y\)-intercept is the point \((0,-8)\).
To find the \(x\)-intercept, let \(f(x)=0\) and solve for \(x\).	\(f(x)=x^{2}-2 x-8\)
	\(0=x^{2}-2 x-8\)
Solve by factoring.	\(0=(x-4)(x+2)\)
	\(0=x-4 \quad 0=x+2\)
	\(4=x \quad-2=x\)
	When \(f(x)=0\), then \(x=4\) or \(x=-2\). The \(x\)-intercepts are the points \((4,0)\) and \((-2,0)\).

Choose integer values for \(x\), substitute them into the equation and simplify to find \(f(x)\). Record the values of the ordered pairs in the chart.	$.$
Plot the points, and then connect them with a smooth curve. The result will be the graph of the function \(f(x)=x^{2}-1\).	$.$

	$.$
To find the \(y\)-intercept, let \(x=0\) and solve for \(f(x)\).	$.$
	$.$
	When \(x=0\), then \(f(0)=4\). The \(y\)-intercept is the point \((0,4)\).
To find the \(x\)-intercept, let \(f(x)=0\) and solve for \(x\).	$.$
	$.$
Find the value of the discriminant to predict the number of solutions which is also the number of \(x\)-intercepts.
\(\begin{array}{c}{b^{2}-4 a c} \\ {1^{2}-4 \cdot 5 \cdot 4} \\ {1-80} \\ {-79}\end{array}\)
	Since the value of the discriminant is negative, there is no real solution to the equation. There are no \(x\)-intercepts.

Step 1: Determine whether the parabola opens upward or downward.	Look \(a\) in the equation \(f(x)=x^{2}-6x+8\) Since \(a\) is positive, the parabola opens upward.	\(f(x)=x^{2}-6x+8\) \(\color{red}{a=1, b=-6, c=8}\) The parabola opens upward.
Step 2: Find the axis of symmetry.	\(f(x)=x^{2}-6x+8\) The axis of symmetry is the line \(x=-\frac{b}{2 a}\).	Axis of Symmetry \(x=-\frac{b}{2 a}\) \(x=-\frac{(-6)}{2 \cdot 1}\) \(x=3\) The axis of symmetry is the line \(x=3\).
Step 3: Find the vertex.	The vertex is on the axis of symmetry. Substitute \(x=3\) into the function.	Vertex \(f(x)=x^{2}-6x+8\) \(f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8\) \(f(3)=-1\) The vertex is \((3,-1)\).
Step 4: Find the \(y\)-intercept. Find the point symmetric to the \(y\)-intercept across the axis of symmetry.	We find \(f(0)\). We use the axis of symmetry to find a point symmetric to the \(y\)-intercept. The \(y\)-intercept is \(3\) units left of the axis of symmetry, \(x=3\). A point \(3\) units to the right of the axis of symmetry has \(x=6\).	\(y\)-intercept \(f(x)=x^{2}-6 x+8\) \(f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8\) \(f(0)=8\) The \(y\)-intercept is \((0,8)\). Point symmetric to \(y\)-intercept: The point is \((6,8)\).
Step 5: Find the \(x\)-intercepts. Find additional points if needed.	We solve \(f(x)=0\). We can solve this quadratic equation by factoring.	\(x\)-intercepts \(f(x)=x^{2}-6 x+8\) \(\color{red}{0}\color{black}{=}x^{2}-6x+8\) \(\color{red}{0}\color{black}{=}(x-2)(x-4)\) \(x=2 or x=4\) The \(x\)-intercepts are \((2,0)\) and \((4,0)\).
Step 6: Graph the parabola.	We graph the vertex, intercepts, and the point symmetric to the \(y\)-intercept. We connect these \(5\) points to sketch the parabola.	$Screenshot (1).png$

	$.$
Since \(a\) is \(-1\), the parabola opens downward.
	$.$
To find the equation of the axis of symmetry, use \(x=-\frac{b}{2 a}\).	\(x=-\frac{b}{2 a}\)
	\(x=-\frac{6}{2(-1)}\)
	\(x=3\)
	The axis of symmetry is \(x=3\). The vertex is on the line \(x=3\).
	$.$
Find \(f(3)\).	\(f(x)=-x^{2}+6 x-9\)
	$.$
	\(f(3)=-9+18-9\)
	\(f(3)=0\)
	The vertex is \((3,0)\).
	$.$
The \(y\)-intercept occurs when \(x=0\). Find \(f(0)\).	\(f(x)=-x^{2}+6 x-9\)
Substitute \(x=0\).	$.$
Simplify.	\(f(0)=-9\)
The point \((0,-9)\) is three units to the left of the line of symmetry. The point three units to the right of the line of symmetry is \((6,-9)\).	$.$
	Point symmetric to the \(y\)-intercept is \((6,-9)\)
The \(x\)-intercept occurs when \(f(x)=0\).	$.$
Find \(f(x)=0\).	$.$
Factor the GCF.	$.$
Factor the trinomial.	$.$
Solve for \(x\).	$.$
Connect the points to graph the parabola.	$.$

	$.$
Since \(a\) is \(2\), the parabola opens upward.	$.$
To find the equation of the axis of symmetry, use \(x=-\frac{b}{2 a}\).	\(x=-\frac{b}{2 a}\)
	\(x=-\frac{-4}{2 \cdot 2}\)
	\(x=1\)
	The equation of the axis of symmetry is \(x=1\).
The vertex is on the line \(x=1\).	\(f(x)=2 x^{2}-4 x-3\)
Find \(f(1)\).	$.$
	\(f(1)=2-4-3\)
	\(\f(1)=-5)
	The vertex is \((1,-5)\).
The \(y\)-intercept occurs when \(x=0\).	\(f(x)=2 x^{2}-4 x-3\)
Find \(f(0)\).
Simplify.	\(f(0)=-3\)
	The \(y\)-intercept is \((0,-3)\).
The point \((0,-3)\) is one unit to the left of the line of symmetry.	Point symmetric to the \(y\)-intercept is \((2,-3)\)
The point one unit to the right of the line of symmetry is \((2,3)\).
The \(x\)-intercept occurs when \(y=0\).	\(f(x)=2 x^{2}-4 x-3\)
Find \(f(x)=0\).
Use the Quadratic Formula.	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Substitute in the values of \(a,b\) and \(c\).	\(x=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(2)(3)}}{2(2)}\)
Simplify.	\(x=\frac{-4 \pm \sqrt{16+24}}{4}\)
Simplify inside the radical.	\(x=\frac{4 \pm \sqrt{40}}{4}\)
Simplify the radical.	\(x=\frac{4 \pm 2 \sqrt{10}}{4}\)
Factor the GCF.	\(x=\frac{2(2 \pm \sqrt{10})}{4}\)
Remove common factors.	\(x=\frac{2 \pm \sqrt{10}}{2}\)
Write as two equations.	\(x=\frac{2+\sqrt{10}}{2}, \quad x=\frac{2-\sqrt{10}}{2}\)
Approximate the values.	\(x \approx 2.5, \quad x \approx-0.6\)
	The approximate values of the \(x\)-intercepts are \((2.5,0)\) and \((-0.6,0)\).
Graph the parabola using the points found.	$.$

	\(f(x)=x^{2}+2 x-8\)
Since \(a\) is positive, the parabola opens upward. The quadratic equation has a minimum.
Find the equation of the axis of symmetry.	\(x=-\frac{b}{2 a}\)
	\(x=-\frac{2}{2 \times 1}\)
	\(x=-1\)
	The equation of the axis of symmetry is \(x=-1\).
The vertex is on the line \(x=-1\).	\(f(x)=x^{2}+2 x-8\)
Find \(f(-1)\).	$.$
	\(f(-1)=1-2-8\)
	\(f(-1)=-9\)
	The vertex is \((-1,-9)\).
Since the parabola has a minimum, the \(y\)-coordinate of the vertex is the minimum \(y\)-value of the quadratic equation. The minimum value of the quadratic is \(-9\) and it occurs when \(x=-1\).
	$.$