3.4e: Exercises - Polynomial Graphs

Last updated
Save as PDF

Page ID: 45428

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A: Concepts

Exercise $\PageIndex{A}$

1) What is the difference between an $x$-intercept and a zero of a polynomial function $f$?

2) If a polynomial function of degree $n$ has $n$ distinct zeros, what do you know about the graph of the function?

3) What is the relationship between the degree of a polynomial function and the maximum number of turning points in its graph? .

4) Explain how the factored form of the polynomial helps us in graphing it.

5) If the graph of a polynomial just touches the $x$-axis and then changes direction, what can we conclude about the factored form of the polynomial?

Answers to odd exercises:

1. The $x$-intercept is where the graph of the function crosses the $x$-axis, and the zero of the function is the input value for which $f(x)=0$.

3. The maximum number of turning points is one less than the degree of the polynomial.

5. There will be a factor raised to an even power.

B: Multiplicity from an Equation

Exercise $\PageIndex{B}$

$ \bigstar $ Find the zeros and give the multiplicity of each.

6) $f(x)=(x+2)^3(x−3)^2$

7) $f(x)=x^2(2x+3)^5(x−4)^2$

8) $f(x)=x^3(x−1)^3(x+2)$

9) $f(x)=x^2(x^2+4x+4)$

10) $f(x)=(2x+1)^3(9x^2−6x+1)$

11) $f(x)=(3x+2)^5(x^2−10x+25)$

12) $f(x)=x(4x^2−12x+9)(x^2+8x+16)$

13) $f(x)=x^6−x^5−2x^4$

14) $f(x)=3x^4+6x^3+3x^2$

15) $f(x)=4x^5−12x^4+9x^3$

16) $f(x)=2x^4(x^3−4x^2+4x)$

17) $f(x)=4x^4(9x^4−12x^3+4x^2)$

Answers to odd exercises:

7. $0$ and $4$ with multiplicity $2$, $−\dfrac{3}{2}$ with multiplicity $5$

9. $0$ with multiplicity $2$, $-2$ with multiplicity $2$

11. $−\dfrac{2}{3}$ with multiplicity $5$, $5$ with multiplicity $2$

13. $0$ with multiplicity $4$, $2$ and $-1$ with multiplicity $1$

15. $\dfrac{3}{2}$ with multiplicity $2$, $0$ with multiplicity $3$

17. $0$ with multiplicity $6$, $\dfrac{2}{3}$ with multiplicity $2$

C: Multiplicity from a Graph

Exercise $\PageIndex{C}$

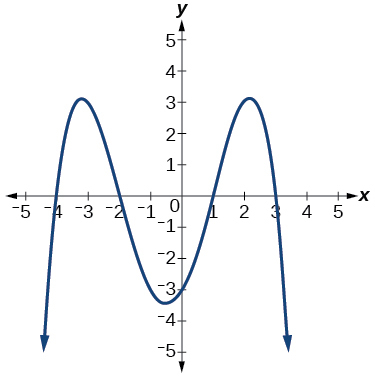
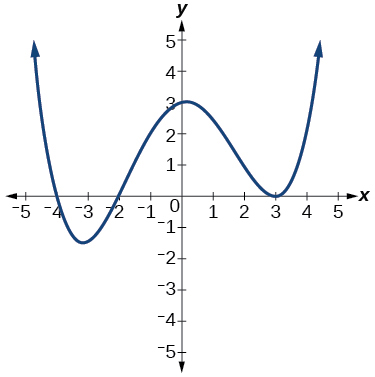
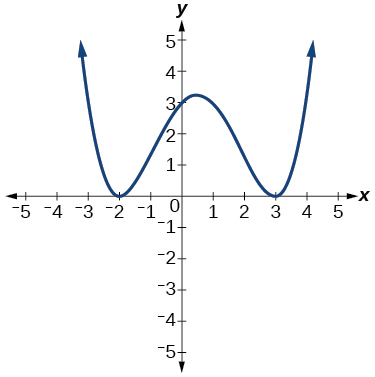
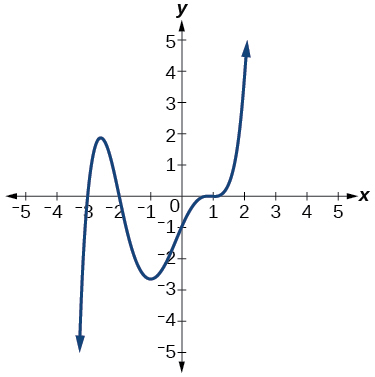
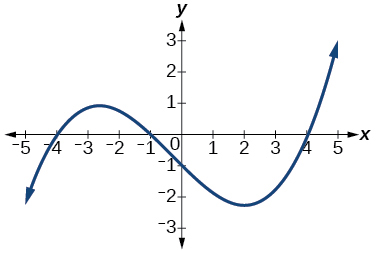
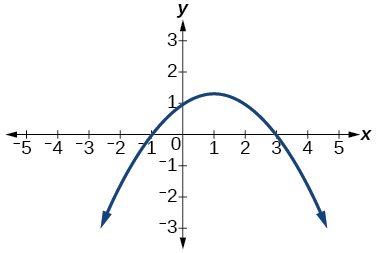
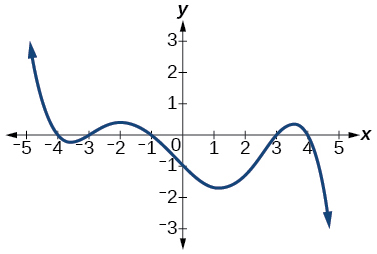
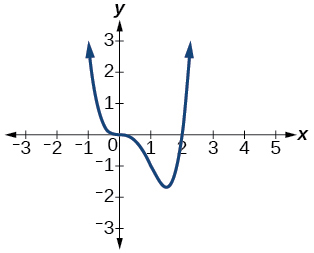
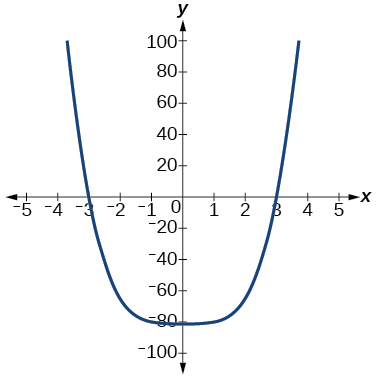
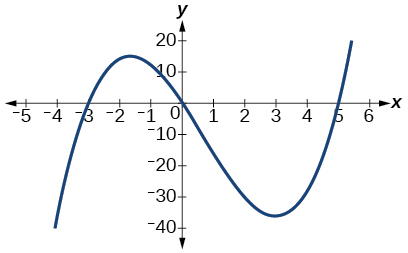
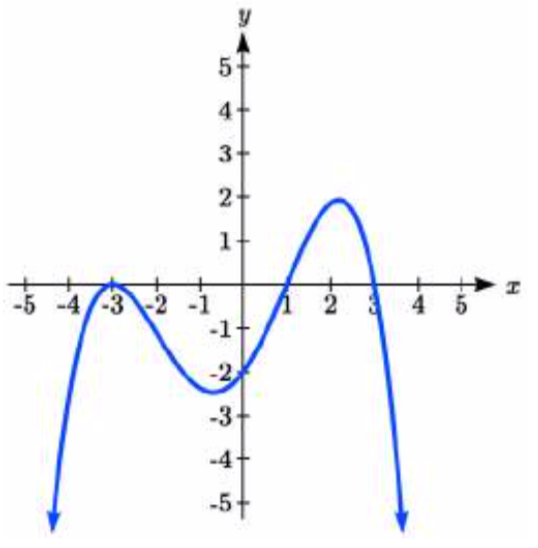
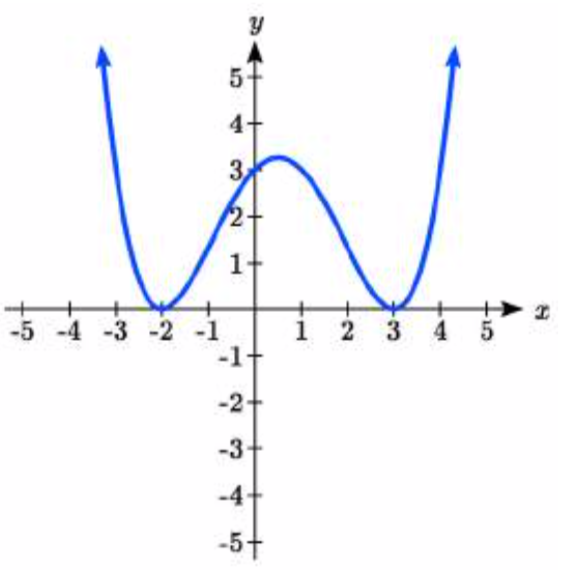
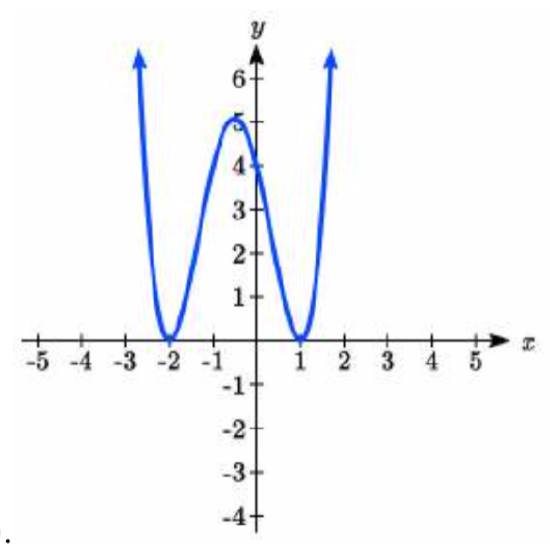
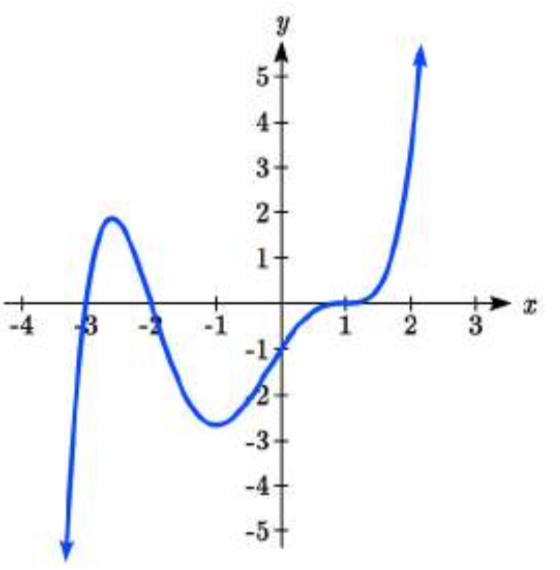
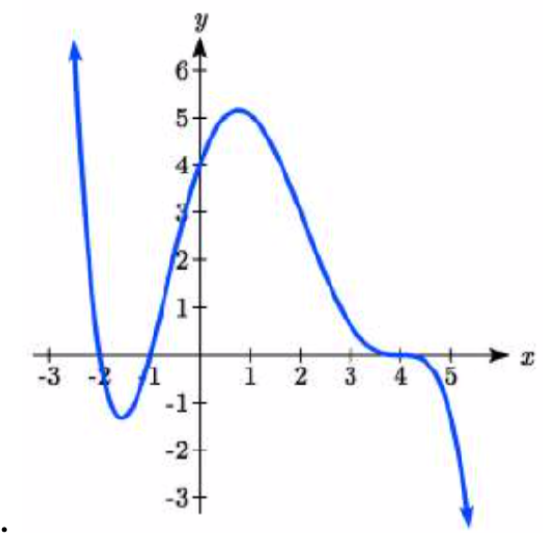
$ \bigstar $ Use the graph to identify zeros and multiplicity.

19)

$CNX_PreCalc_Figure_03_04_212.jpg$

20)

$CNX_PreCalc_Figure_03_04_213.jpg$

21)

$CNX_PreCalc_Figure_03_04_214.jpg$

22)

$CNX_PreCalc_Figure_03_04_215.jpg$

Answers to odd exercises:

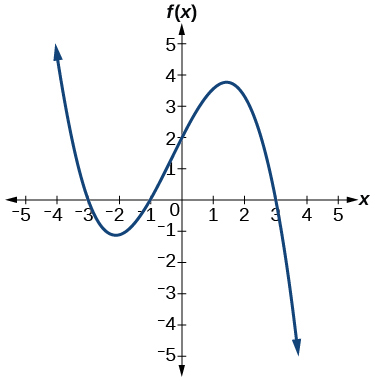
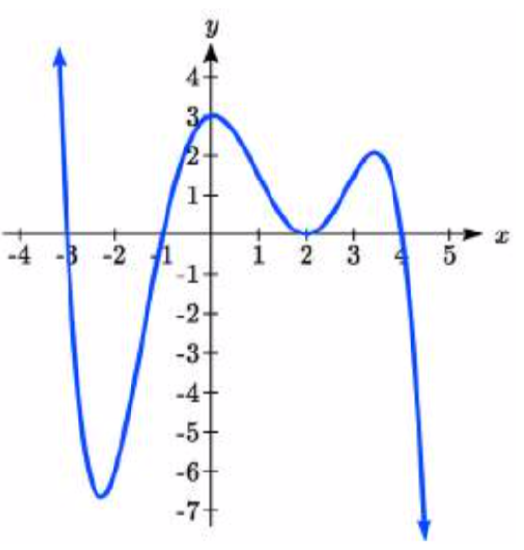
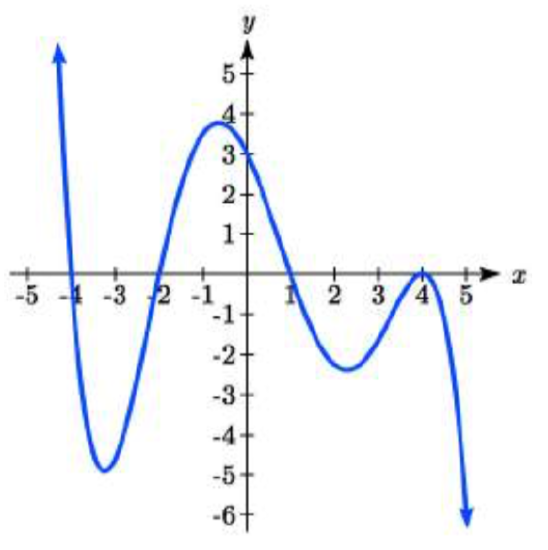
19. $–4, –2, 1, 3$ with multiplicity $1$

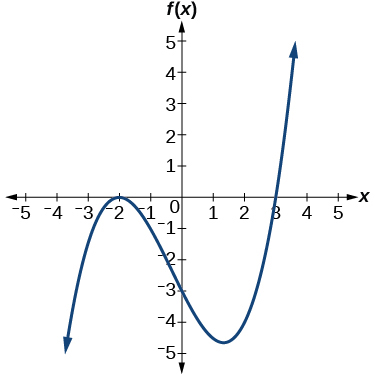
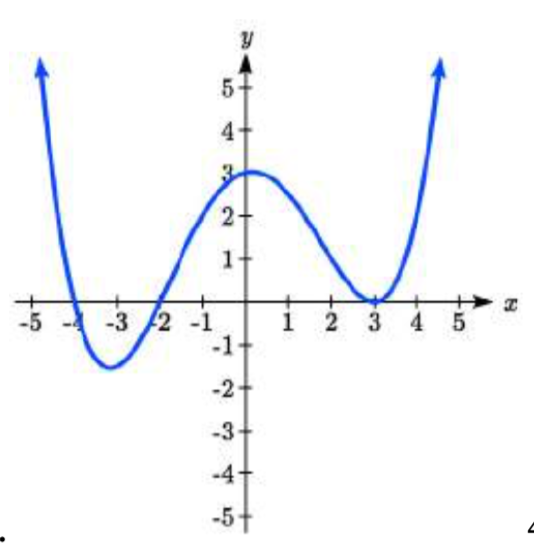
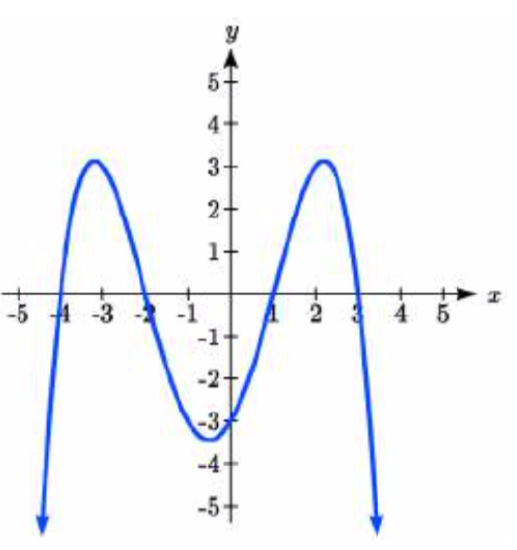
21. $–2, 3$ each with multiplicity $2$

D: Graph polynomials

Exercise $\PageIndex{D}$

$ \bigstar $ Graph the polynomial functions. State the $x$- and $y$- intercepts, multiplicity, and end behavior.

24) $f(x)=(x+3)^2(x−2)$

25) $g(x)=(x+4)(x−1)^2$

26) $h(x)=(x−1)^3(x+3)^2$

27) $k(x)=(x−3)^3(x−2)^2 $

28) $m(x)=−2x(x−1)(x+3)$

29) $n(x)=−3x(x+2)(x−4)$

30. $a(x) = x(x + 2)^{2}$

31. $g(x) = x(x + 2)^{3}$

32. $f(x) = -2(x-2)^2(x+1)$

33. $g(x) = (2x+1)^2(x-3)$

34. $f(x) = x^{3}(x + 2)^{2}$

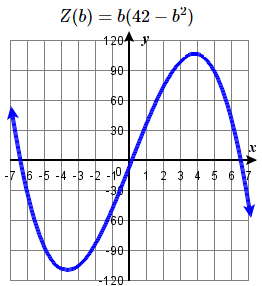
35. $P(x) = (x - 1)(x - 2)(x - 3)(x - 4)$

36. $q(x) = (x + 5)^{2}(x - 3)^{4}$

37. $h(x) = x^2(x-2)^2(x+2)^2$

38. $h(t) = (3-t)(t^2+1)$

39. $Z(b) = b(42 - b^{2})$

Answers to odd exercises:

25. $x$-intercepts, $(1, 0)$ with multiplicity $2$, $(–4, 0)$ with multiplicity $1$, $y$- intercept $(0, 4)$ . As $x→−∞$, $f(x)→−∞$, as $x→∞,$ $f(x)→∞$.

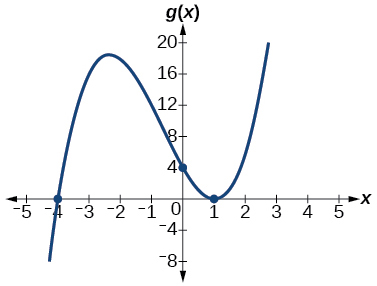
$CNX_Precalc_Figure_03_04_202.jpg$

27. $x$-intercepts $(3,0)$ with multiplicity $3$, $(2,0)$ with multiplicity $2$, $y$- intercept $(0,–108).$ As $x→−∞,$ $f(x)→−∞$, as $x→∞,$ $f(x)→∞$.

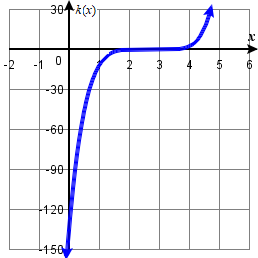
$3.4 example 27.png$

29. $x$-intercepts $(0, 0),(–2, 0),(4, 0)$ with multiplicity $1$, $y$-intercept (0, 0). As $x→−∞,$ $f(x)→∞$, as $x→∞,$ $f(x)→−∞$.

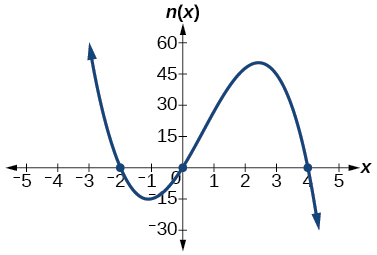
$CNX_Precalc_Figure_03_04_206.jpg$

31. $ (-2,0) $ multiplicity $3$,
   $(0,0)$ multiplicity 1,
   y-intercept $(0 ,0 )$,
end behaviour: $ \nwarrow \dots \nearrow $
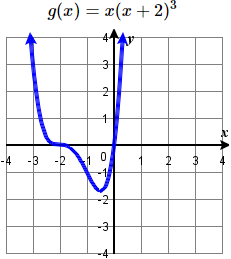
   $3.4 example 31.png$

33. $(-\frac{1}{2} ,0 )$ multiplicity $2$,
   $(3 ,0 )$ multiplicity $1$,
   y-intercept $(0 ,-3 )$,
   end behaviour: $ \swarrow \dots \nearrow $
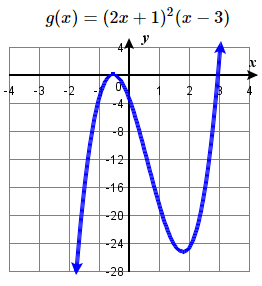
$3.4 example 33.png$

35. $(1 ,0 )$, $(2 ,0 )$, $(3 ,0 )$, $(4 ,0 )$
all multiplicity $1$,
y-intercept $(0 , 24)$,
end behaviour: $ \nwarrow \dots \nearrow $
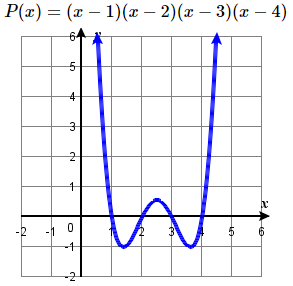
$3.4 example 35.png$

37. $(-2 ,0 )$, $(2 ,0 )$, $(0 ,0 )$
  all multiplicity $2$, y-intercept $(0 ,0 )$,
  end behaviour: $ \nwarrow \dots \nearrow $
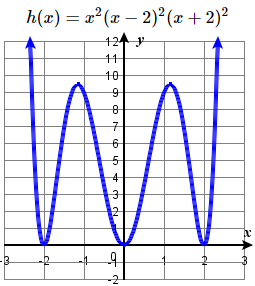
   $3.4 example 37.png$

39. $(\sqrt{42} ,0 )$, $(-\sqrt{42} ,0 )$, $(0 ,0 )$
all multiplicity $1$, y-intercept $(0 ,0 )$,
end behaviour: $ \nwarrow \dots \searrow $
$3.4 example 39.png$

$ \bigstar $ Graph the polynomial functions. State the $x$- and $y$- intercepts, multiplicity, and end behavior.

41. $f\left(x\right)=\left(x+3\right)^{2} (x-2)$

42. $g\left(x\right)=\left(x+4\right)\left(x-1\right)^{2}$

43. $h\left(x\right)=\left(x-1\right)^{3} \left(x+3\right)^{2}$

44. $k\left(x\right)=\left(x-3\right)^{3} \left(x-2\right)^{2}$

45. $m\left(x\right)=-2x\left(x-1\right)(x+3)$

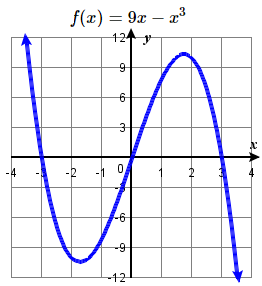
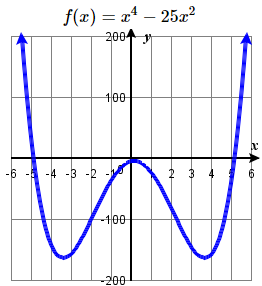
46. $n\left(x\right)=-3x\left(x+2\right)(x-4)$

47. $f(x) = 9x - x^3$

48. $f(x) =8 + x^3 $

49. $f(x) = x^4 - 25x^2$

50. $ f(x) =16 - x^4 $

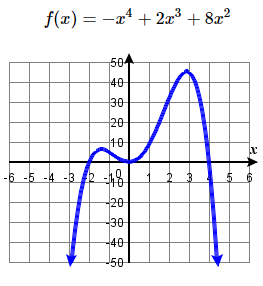
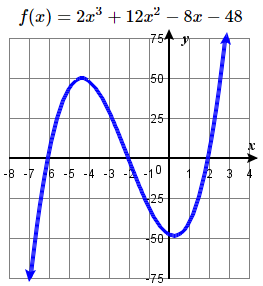
51. $f(x) = -x^4 + 2x^3 + 8x^2$

52. $f(x) =x^3+7x^2 -9x $

53. $f(x) = 2x^3 + 12x^2 - 8x - 48$

54. $f(x) = 4x^4 + 10x^3 - 4x^2 -10x $

Answers to odd exercises:

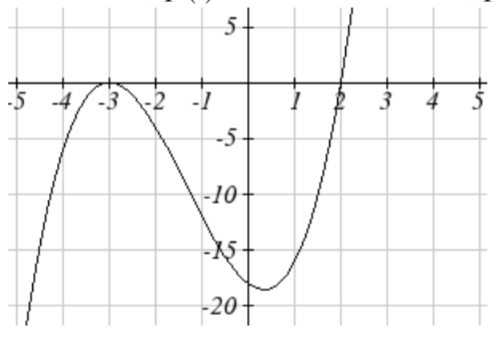
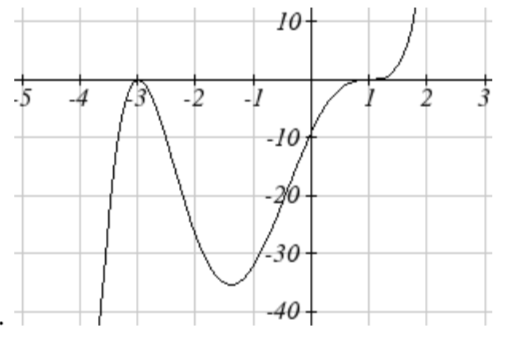
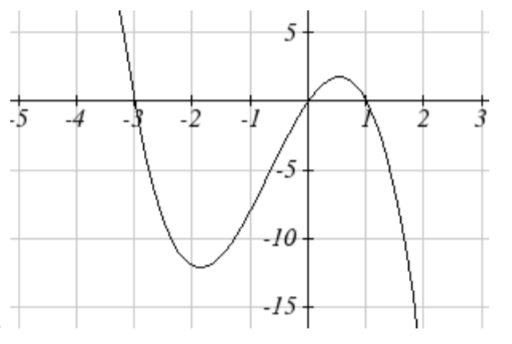
41. $(-3 ,0 )$ multiplicity $2$, $(2 ,0 )$ multiplicity $1$, y-intercept$(0 ,-18 )$, $ \swarrow \dots \nearrow $ $Screen Shot 2019-10-03 at 6.05.35 PM.png$	43. $( -3, 0)$ multiplicity $2$, $(1 , 0) $ multiplicity $3$, y-intercept$( 0, -9)$, $ \swarrow \dots \nearrow $ $Screen Shot 2019-10-03 at 6.05.54 PM.png$	45. $(-3 , 0)$, $(0 , 0)$, $(1 , 0)$ all multiplicity $1$, y-intercept$(0 ,0 )$, $ \nwarrow \dots \searrow $ $Screen Shot 2019-10-03 at 6.06.33 PM.png$
47. $(-3 , 0)$, $(0 , 0)$, $(3 , 0)$ all multiplicity $1$, y-intercept $(0 ,0 )$, $ \nwarrow \dots \searrow $ $3.4 example 47.png$	49. $( -5, 0) $, $( 5, 0) $ both multiplicity $1$, $(0 , 0)$ multiplicity $2$, y-intercept $(0 ,0 )$, $ \nwarrow \dots \nearrow $ $3.4 example 49.png$	51. $( -2, 0)$, $( 4, 0)$ both multiplicity $1$, $(0 , 0)$ multiplicity $2$, y-intercept $(0 ,0 )$, $ \swarrow \dots \searrow $ $3.4 example 51.png$
53. $(-6 , 0)$, $(-2 , 0)$, $(2 , 0)$ all multiplicity $1$, y-intercept $(0 , -48)$, $ \swarrow \dots \nearrow $ $3.4 example 53.png$

E: Polynomial Degree from a Graph

Exercise $\PageIndex{E}$

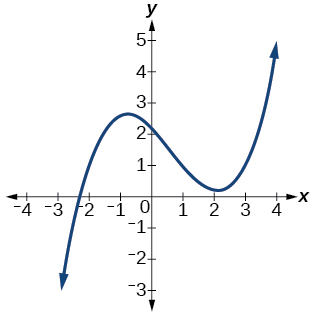
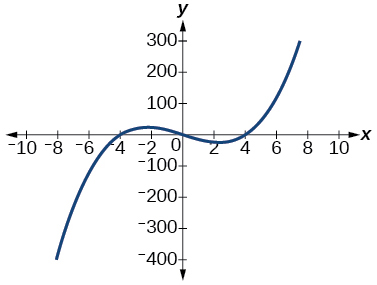
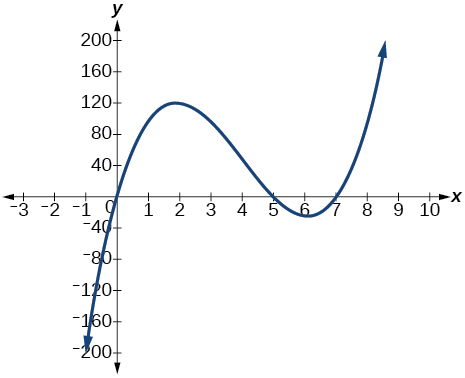
$ \bigstar $ Determine the least possible degree of the polynomial function shown.

61)

$CNX_Precalc_Figure_03_03_201.jpg$

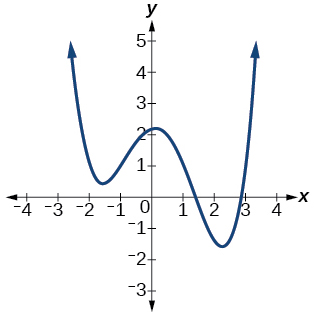
62)

$CNX_Precalc_Figure_03_03_202.jpg$

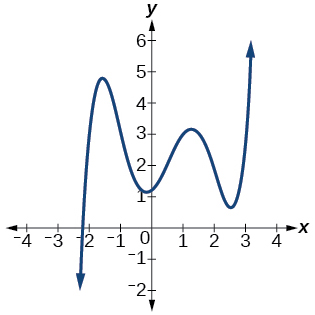
63)

$CNX_Precalc_Figure_03_03_203.jpg$

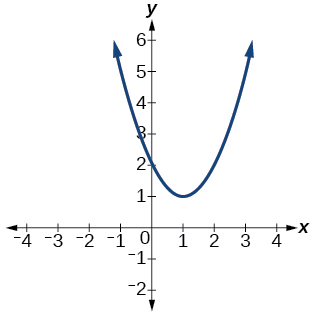
64)

$CNX_Precalc_Figure_03_03_204.jpg$

65)

$CNX_Precalc_Figure_03_03_205.jpg$

66)

$CNX_Precalc_Figure_03_03_206.jpg$

67)

$CNX_Precalc_Figure_03_03_207.jpg$

68)

$CNX_Precalc_Figure_03_03_208.jpg$

Answers to odd exercises:: 61. $3$, $\qquad$ 63. $5$, $\qquad$ 65. $3$, $\qquad$ 67. $5$

F: Construct an Equation from a graph

Exercise $\PageIndex{F}$

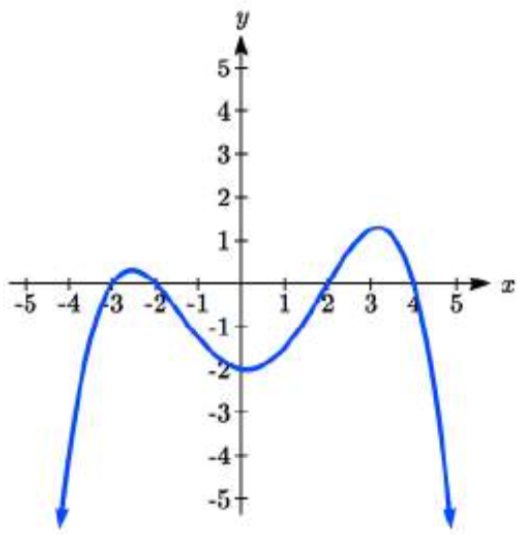
$ \bigstar $ Use the graphs to write the formula for the polynomial function of least degree.

69)

$CNX_PreCalc_Figure_03_04_208.jpg$

70)

$CNX_Precalc_Figure_03_04_207.jpg$

71)

$CNX_PreCalc_Figure_03_04_210.jpg$

72)

$CNX_PreCalc_Figure_03_04_209.jpg$

73.

$屏幕快照 2019-06-23 上午3.25.44.png$

74)

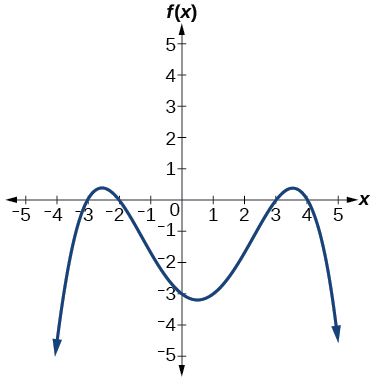$CNX_PreCalc_Figure_03_04_211.jpg$

Answers to odd exercises:

69. $ f(x) = -(x+3)(x+1)(x-3)$ or $ f(x) = -\frac{2}{9}(x+3)(x+1)(x-3)$
71. $ f(x) = (x+2)^2(x-3)$ or $ f(x) = \frac{1}{4}(x+2)^2(x-3)$
73. $ f(x) = -(x+3)(x+2)(x-2)(x-4) $ or $ f(x) = -\frac{1}{24}(x+3)(x+2)(x-2)(x-4) $

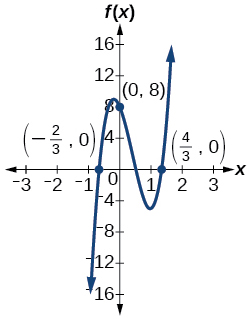
$ \bigstar $ Use the graphs to write a formula for the polynomial function of least degree.

75)

$CNX_PreCalc_Figure_03_04_217.jpg$

76)

$CNX_PreCalc_Figure_03_04_216.jpg$

77)

$CNX_PreCalc_Figure_03_04_218.jpg$

78)

$CNX_Precalc_Figure_03_03_216.jpg$

79)

$CNX_Precalc_Figure_03_03_222.jpg$

80)

$CNX_Precalc_Figure_03_03_220.jpg$

81)

$CNX_Precalc_Figure_03_03_218.jpg$

82)

$CNX_Precalc_Figure_03_03_224.jpg$

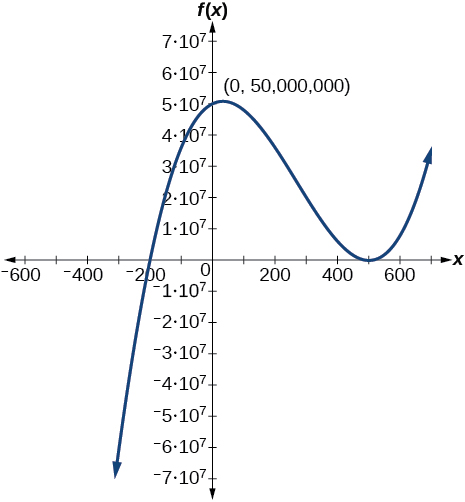
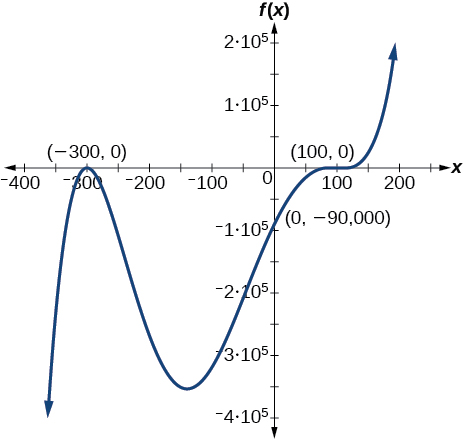
Answers to odd exercises:: 75. $f(x)=(x−500)^2(x+200)$ 77. $f(x)=(x+300)^2(x-100)^3$
79. $f(x)=(x+3)(x-3)(x^2+10)$ 81. $f(x)=4x(x-5)(x-7)$

$ \bigstar $ Use the graphs to write a formula for the polynomial function of least degree.

83.

$屏幕快照 2019-06-23 上午3.26.29.png$

84(a).

$屏幕快照 2019-06-23 上午3.26.12.png$

84(b).

$屏幕快照 2019-06-23 上午3.26.46.png$

85.

$屏幕快照 2019-06-23 上午5.32.03.png$

86.

$屏幕快照 2019-06-23 上午5.32.31.png$

87.

$屏幕快照 2019-06-23 上午5.32.47.png$

88.

$屏幕快照 2019-06-23 上午5.33.17.png$

89.

. $屏幕快照 2019-06-23 上午5.33.39.png$

90.

$屏幕快照 2019-06-23 上午5.34.00.png$

Answers to odd exercises:

83. $y = \dfrac{1}{24} (x + 4) (x + 2) (x - 3)^2$

85. $y = \dfrac{1}{12} (x + 2)^2 (x - 3)^2$

87. $y = \dfrac{1}{6} (x + 3) (x + 2) (x - 1)^3$

89. $y = -\dfrac{1}{16} (x + 3)(x + 1) (x - 2)^2 (x - 4)$

G: Construct an Equation from a Description

Exercise $\PageIndex{G}$

$ \bigstar $ Use the information about the graph of a polynomial function to determine the function. Assume the leading coefficient is $1$ or $-1$. There may be more than one correct answer.

91) The $y$-intercept is $(0,−4)$. The $x$-intercepts are $(−2,0), (2,0)$. Degree is $2$. End behavior: $ \nwarrow \dots \nearrow $

92) The $y$-intercept is $(0,9)$. The $x$-intercepts are $(−3,0), (3,0)$. Degree is $2$. End behavior: $ \swarrow \dots \searrow $

93) The $y$-intercept is $(0,0)$. The $x$-intercepts are $(0,0), (2,0)$. Degree is $3$. End behavior: $ \swarrow \dots \searrow $

94) The $y$-intercept is $(0,1)$. The x-intercept is $(1,0)$. Degree is $3$. End behavior: $ \nwarrow \dots \searrow $

95) The $y$-intercept is $(0,1)$. There is no $x$-intercept. Degree is $4$. End behavior: $ \nwarrow \dots \nearrow $

$ \bigstar $ Use the given information about the polynomial graph to write the equation.

97) Degree $3$. Zeros at $x=–2$,$x=1$, and $x=3$. $y$-intercept at $(0,–4)$

98) Degree $3$. Zeros at $x=–5$, $x=–2$, and $x=1$. $y$-intercept at $(0,6)$

99) Degree $5$. Roots of multiplicity $2$ at $x=3$ and $x=1$. Root of multiplicity $1$ at $x=–3$.
$\quad$$y$-intercept at $(0,9)$

100) Degree $4$. Root of multiplicity $2$ at $x=4$. Roots of multiplicity $1$ at $x=1$ and $x=–2$.
$\quad$$y$-intercept at $(0,–3)$

101) Degree $5$. Double zero at $x=1$. Triple zero at $x=3$. Passes through the point $(2,15)$

102) Degree $3$. Zeros at $x=4$, $x=3$, and $x=2$. $y$-intercept at $(0,−24)$

103) Degree $3$. Zeros at $x=−3$, $x=−2$ and $x=1$. $y$-intercept at $(0,12)$

104) Degree $5$. Roots of multiplicity $2$ at $x=−3$ and $x=2$. Root of multiplicity $1$ at $x=−2$. $y$-intercept at $(0, 4)$.

105) Degree $4$. Roots of multiplicity $2$ at $x=\dfrac{1}{2}$. Roots of multiplicity $1$ at $x=6 $ and $x=−2$. $y$-intercept at $(0,18)$

106) Double zero at $x=−3$. Triple zero at $x=0$. Passes through the point $(1,32)$.

107. Degree 3. Zeros at $x$ = -2, $x$ = 1, and $x$ = 3. Vertical intercept at (0, -4)

108. Degree 3. Zeros at $x$ = -5, $x$ = -2, and $x$ = 1. Vertical intercept at (0, 6)

109. Degree 5. Roots of multiplicity 2 at $x$ = 3 and $x$ = 1. Root of multiplicity 1 at $x$ = -3. Vertical intercept at (0, 9)

110. Degree 4. Root of multiplicity 2 at $x$ = 4. Roots of multiplicity 1 at $x$ = 1 and $x$ = -2.
$\quad$Vertical intercept at (0, -3)

111. Degree 5. Double zero at $x$ = 1. Triple zero at $x$ = 3. Passes through the point (2, 15)

112. Degree 5. Single zero at $x$ = -2 and $x$ = 3. Triple zero at $x$ = 1. Passes through the point (2, 4)

Answers to odd exercises:

91. $f(x)=x^2−4$

93. $f(x)=x^3−4x^2+4x$

95. $f(x)=x^4+1$

97. $f(x)=−\dfrac{2}{3}(x+2)(x−1)(x−3)$

99. $f(x)=\dfrac{1}{3}(x−3)^2(x−1)^2(x+3)$

101. $ f(x) =−15(x−1)^2(x−3)^3$

103. (f(x)=−2(x+3)(x+2)(x−1)\)

105. $f(x)=−\dfrac{3}{2}(2x−1)^2(x−6)(x+2)$

107. $y = -\dfrac{2}{3} (x + 2) (x - 1) (x - 3)$

109. $y = \dfrac{1}{3} (x - 1)^2 (x - 3)^2 (x + 3)$

111. $y = -15(x - 1)^2 (x - 3)^3$

H: Turning Points

Exercise $\PageIndex{H}$

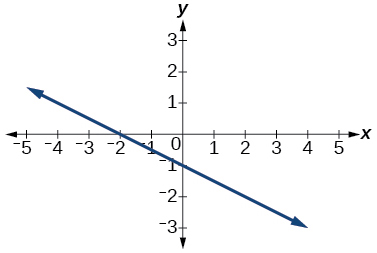
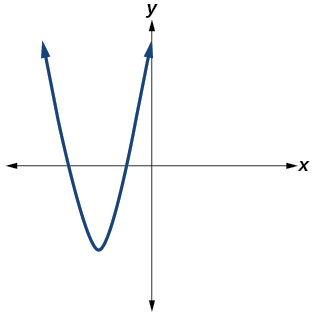
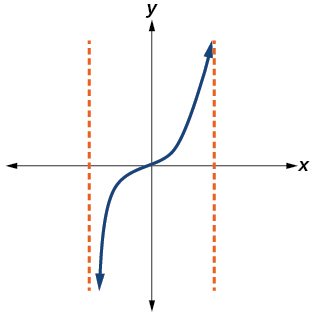
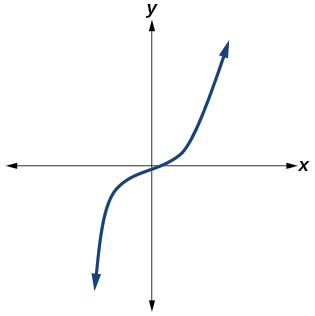
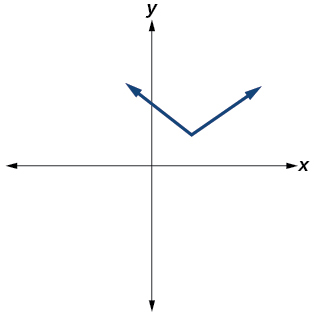
$ \bigstar $ Determine whether the graph of the function provided is a graph of a polynomial function. If so, determine the number of turning points and the least possible degree for the function.

115)

$CNX_Precalc_Figure_03_03_209.jpg$

116)

$CNX_Precalc_Figure_03_03_210.jpg$

117)

$CNX_Precalc_Figure_03_03_211.jpg$

118)

$CNX_Precalc_Figure_03_03_212.jpg$

119)

$CNX_Precalc_Figure_03_03_213.jpg$

120)

$CNX_Precalc_Figure_03_03_214.jpg$

121)

$CNX_Precalc_Figure_03_03_215.jpg$

Answers to odd exercises:

115. Yes. Number of turning points is $2$. Least possible degree is $3$.

117. Yes. Number of turning points is $1$. Least possible degree is $2$.

119. Yes. Number of turning points is $0$. Least possible degree is $1$.

212. Yes. Number of turning points is $0$. Least possible degree is $1$.

$ \star $

41. \((-3 ,0 )\) multiplicity \(2\), \((2 ,0 )\) multiplicity \(1\), y-intercept\((0 ,-18 )\), \( \swarrow \dots \nearrow \) $Screen Shot 2019-10-03 at 6.05.35 PM.png$	43. \(( -3, 0)\) multiplicity \(2\), \((1 , 0) \) multiplicity \(3\), y-intercept\(( 0, -9)\), \( \swarrow \dots \nearrow \) $Screen Shot 2019-10-03 at 6.05.54 PM.png$	45. \((-3 , 0)\), \((0 , 0)\), \((1 , 0)\) all multiplicity \(1\), y-intercept\((0 ,0 )\), \( \nwarrow \dots \searrow \) $Screen Shot 2019-10-03 at 6.06.33 PM.png$
47. \((-3 , 0)\), \((0 , 0)\), \((3 , 0)\) all multiplicity \(1\), y-intercept \((0 ,0 )\), \( \nwarrow \dots \searrow \) $3.4 example 47.png$	49. \(( -5, 0) \), \(( 5, 0) \) both multiplicity \(1\), \((0 , 0)\) multiplicity \(2\), y-intercept \((0 ,0 )\), \( \nwarrow \dots \nearrow \) $3.4 example 49.png$	51. \(( -2, 0)\), \(( 4, 0)\) both multiplicity \(1\), \((0 , 0)\) multiplicity \(2\), y-intercept \((0 ,0 )\), \( \swarrow \dots \searrow \) $3.4 example 51.png$
53. \((-6 , 0)\), \((-2 , 0)\), \((2 , 0)\) all multiplicity \(1\), y-intercept \((0 , -48)\), \( \swarrow \dots \nearrow \) $3.4 example 53.png$