Skip to main content
Mathematics LibreTexts

3.9e: Exercises - Rational Functions

  1. Last updated
  2. Save as PDF
  • Page ID
    89332

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A: Conceptual Questions 

    Exercise \(\PageIndex{A}\)

    1. What is the fundamental difference in the algebraic representation of a polynomial function and a rational function?

    2. What is the fundamental difference in the graphs of polynomial functions and rational functions?

    3. If the graph of a rational function has a removable discontinuity, what must be true of the functional rule?

    4. Can a graph of a rational function have no vertical asymptote? If so, how?

    5. Can a graph of a rational function have no x-intercepts? If so, how?

    Answers to odd exercises.

    1. The rational function will be represented by a quotient of polynomial functions.
    3. The numerator and denominator must have a common factor.
    5. Yes. The numerator of the formula of the functions would have only complex roots and/or factors common to both the numerator and denominator. 

    B: Find Domain of Rational Functions

    Exercise \(\PageIndex{B}\)

    \( \bigstar \) Find the domain of the rational functions.

    7. \(f(x)=\dfrac{x+1}{x^{2}-1}\) 8. \(f(x)=\dfrac{x-1}{x+2}\) 9. \(f(x)=\dfrac{x^{2}+4 x-3}{x^{4}-5 x^{2}+4}\) 10. \(f(x)=\dfrac{x^{2}+4}{x^{2}-2 x-8}\)
    Answers to odd exercises.

    7. All reals except that \(x \neq -1,1\)
    9. All reals except that \(x \neq-1,-2,1,2\) 

    C: Find domain, vertical asymptotes, holes, and horizontal asymptotes

    Exercise \(\PageIndex{C}\)

    \( \bigstar \) For each function, find (a) the domain, vertical asymptotes and holes, and (b) the horizontal asymptote and points of intersection of the HA with the function.  

    1. \(f(x)=\dfrac{2x^2}{3x^2+1}\)
    2. \(f(x)=\dfrac{4}{x-1}\)
    3. \(f(x)=\dfrac{2x-2}{5x^2-3x-2}\)
    1. \(f(x)=\dfrac{x+2}{x^{2}-9}\)
    2. \(f(x)=\dfrac{x}{x^{2}+5 x-36}\)
    3. \(f(x)=\dfrac{3+x}{x^{3}-27}\)
    1. \(f(x)=\dfrac{3x-4}{x^{3}-16x}\)
    2. \(f(x)=\dfrac{x^3-x}{x^3+9 x^2+14 x}\)
    3. \(f(x)=\dfrac{x+5}{x^{2}-25}\)
    1. \(f(x)=\dfrac{2x-4}{x-6}\)
    2. \(f(x)=\dfrac{4-2x}{3 x-1}\)

    \( \bigstar \) Identify the removable discontinuity ("hole").

    1. \(f(x)=\dfrac{x^{2}-4}{x-2}\)
    2. \(f(x)=\dfrac{x^{3}+1}{x+1}\)
    1. \(f(x)=\dfrac{x^{2}+x-6}{x-2}\)
    1. \(f(x)=\dfrac{2 x^{2}+5 x-3}{x+3}\)
    1. \(f(x)=\dfrac{x^{3}+x^{2}}{x+1}\)
    Answers to odd exercises.

    11. Domain is all reals;  no VA, No holes;      H.A. at \( y = \frac{2}{3} \), No intersection;
    13. Domain is all reals \(x \neq 1,  -\frac{2}{5}\), V.A. at \(x=-\frac{2}{5}\); Hole at \( (1, \frac{2}{7} ) \);      H.A. at \(y=0\); No intersection;
    15. Domain is all reals \(x \neq 4,-9\), V.A. at \(x=4,-9\), No holes;      H.A. at \(y=0\); Intersection at \( (0,0) \);
    17. Domain is all reals \(x \neq 0,4,-4\), V.A. at \(x=0,4,-4\), No holes;      H.A. at \(y=0\); Intersection at \( (\frac{4}{3},0) \);
    19. Domain is all reals \(x \neq 5,-5\), V.A. at \(x=5\), Hole at \( (-5, \frac{-1}{10}); \)      H.A. at \(y=0\); No intersection;
    21. Domain is all reals \(x \neq \frac{1}{3}\), V.A. at \(x=\frac{1}{3}\), No holes;      H.A. at \(y=-\frac{2}{3}\); No intersection;
    25. \((2,4)\)     27. \((2,5)\)     29. \((-1,1)\)

    D: Describe local and end behaviour

    Exercise \(\PageIndex{D}\)

    \( \bigstar \) Describe the local and end behavior of the functions.

    1. \(f(x)=\dfrac{x}{2 x+1}\)
    2. \(f(x)=\dfrac{2x}{x-6}\)
    1. \(f(x)=\dfrac{-2x}{x-6}\)
    2. \(f(x)=\dfrac{x^{2}-4 x+3}{x^{2}-4x-5}\)
    1. \(f(x)=\dfrac{2 x^{2}-32}{6 x^{2}+13x-5}\) 
    Answers to odd exercises.

    31. Local behavior: \(x \rightarrow-\frac{1}{2}^{+}, f(x) \rightarrow-\infty, x \rightarrow-\frac{1}{2}^{-}, f(x) \rightarrow \infty\)
          End behavior: \(x \rightarrow \pm \infty, f(x) \rightarrow \frac{1}{2}\)

    33. Local behavior: \(x \rightarrow 6^{+}, f(x) \rightarrow-\infty, x \rightarrow 6^{-}, f(x) \rightarrow \infty \)
          End behavior: \(x \rightarrow \pm \infty, f(x) \rightarrow-2\)

    35. Local behavior: \( x \rightarrow -\frac{5}{2}^{-}, \; f(x) \rightarrow-\infty,  \quad        x \rightarrow -\frac{5}{2}^{+}, \; f(x) \rightarrow \infty \)
          \( x \rightarrow  \frac{1}{3}^{-}, \; f(x) \rightarrow \infty, \quad      x \rightarrow  \frac{1}{3}^{+}, \; f(x) \rightarrow-\infty, \) \( \quad \)       End behavior: \(x \rightarrow \pm \infty, f(x) \rightarrow \frac{1}{3}\)

    E: Find Slant Asymptote and its intersection with the function

    Exercise \(\PageIndex{E}\)

    \( \bigstar \) For each function, (a) Find the slant asymptote of the functions, (b) Determine any points of intersection between the function and this asymptote.

    1. \(f(x)=\dfrac{24 x^{2}+6 x}{2 x+1}\)
    2. \(f(x)=\dfrac{4 x^{2}-10}{2 x-4}\)
    1. \(f(x)=\dfrac{81 x^{2}-18}{3 x-2}\)
    2. \(f(x)=\dfrac{6 x^{3}-5 x}{3 x^{2}+4}\)

    40.   \(f(x)=\dfrac{x^{2}+5x+4}{x-1} \\ \)
    40.1 \(f(x)=\dfrac{x^3-3x^2-x+3}{x^2-2x-8}\)
    Answers to odd exercises.

    37. \(y=2 x+4\) No point of intersection    39. \(y=2 x\)  Intersection at \( (0, 0) \)

    F: Find Intercepts

    Exercise \(\PageIndex{F}\)

    \( \bigstar \) Find the \(x\)- and \(y\)-intercepts for the functions. 

    43. \(f(x)=\dfrac{x}{x^{2}-x}\)

    44. \(f(x)=\dfrac{x+5}{x^{2}+4}\)

    45.  \(f(x)=\dfrac{x^{2}+x+6}{x^{2}-10 x+24}\)

    46.  \(f(x)=\dfrac{x^{2}+8 x+7}{x^{2}+11 x+30}\)

    48.  \(f(x)=\dfrac{94-2 x^{2}}{3 x^{2}-12}\)
    Answers to odd exercises.

    43. none     45. \(x\) -intercepts none, \(y\) -intercept \(\left(0, \frac{1}{4}\right)\) 

    G: Identify attributes and sketch

    Exercise \(\PageIndex{G}\)

    \( \bigstar \) Find the (a) vertical asymptotes, (b) coordinates of any holes, (c) end behaviour asymptote (horizontal or slant), (d) coordinates of any points of intersection of the function with the end behaviour asymptote, (e) coordinates of any x-intercepts, (f) coordinates of the y-intercept. Use that information to sketch a graph.

    1. \(f(x)=\dfrac{4}{2x-3}\)
    2. \(f(x)=\dfrac{2}{x+1}\)
    3. \(p(x)=\dfrac{2x-3}{x+4}\)
    4. \(q(x)=\dfrac{x-5}{3 x-1}\)
    1. \(s(x)=\dfrac{4}{(x-2)^{2}}\)
    2. \(r(x)=\dfrac{5}{(x+1)^{2}}\)
    3. \(f(x)=\dfrac{x+2}{(x-1)(x-4)}\)
    4. \(f(x)=\dfrac{2}{(x-1)(x+2)}\)
    1. \(f(x)=\dfrac{(x-4)(x+3)^2}{(x+1)(x-4)(x-1)^2}\)
    2. \( f(x) = \dfrac{ (x-2)(x+4)}{ (x-2)(x-3)(x+1)^2} \)
    3. \( f(x) = \dfrac{(x-3)(x+6) }{ (x+2)(x+4)(x-1)(x+6)} \)
    4. \( f(x) = \dfrac{ (x+1)(x-3)(-1)(x+2)}{ (x+1)(x-4)(x+3) } \)
    1. \(f(x)=\dfrac{3 x^{2}-14 x-5}{3 x^{2}+8 x-16}\)
    2. \(g(x)=\dfrac{2 x^{2}+7 x-15}{3 x^{2}-14+15}\)
    3. \(a(x)=\dfrac{x^{2}+2 x-3}{x^{2}-1}\)
    1. \(b(x)=\dfrac{x^{2}-x-6}{x^{2}-4}\)
    2. \(h(x)=\dfrac{2 x^{2}+x-1}{x-4}\)
    3. \(k(x)=\dfrac{2 x^{2}-3 x-20}{x-5}\)
    1. \(w(x)=\dfrac{(x-1)(x+3)(x-5)}{(x+2)^{2}(x-4)}\)
    2. \(z(x)=\dfrac{(x+2)^{2}(x-5)}{(x-3)(x+1)(x+4)} \\[6pt] \)
    1. \( f(x) = \dfrac{ x^2+2}{ x} \)
    2. \( f(x) = \dfrac{x^2+x+1 }{x+1 } \)
    3. \( f(x) = \dfrac{ x^2-3x+2}{x-3 } \)
    4. \( f(x) = \dfrac{ x^3+4x^2-x-4}{ x^2+2x-8} \)
    1. \( f(x) = \dfrac{ x^2+3x+2}{ x-1} \)
    2. \( f(x) = \dfrac{ x^2+3x+2}{ x+3} \)
    3. \( f(x) = \dfrac{x^2+4x+3 }{ x+4} \)
    4. \( f(x) = \dfrac{x^2-3x }{ x-4} \\[6pt] \)
    1. \( f(x) = \dfrac{ x^2-4x+3}{x-2 } \)
    2. \( f(x) = \dfrac{x^2-x-6 }{x-1 } \)
    3. \( f(x) = \dfrac{x^2+2x-8 }{x+1 } \)
    4. \( f(x) = \dfrac{ x^3-x^2-20x}{x^2+3x }\)
    1. \( f(x) = \dfrac{4 x-12}{x^3-3x^2-4x+12 } \)
    2. \( f(x) = \dfrac{2 }{ x^2-7x+10} \)
    3. \( f(x) = \dfrac{x^2+9 }{x^2-16} \)
    4. \( f(x) = \dfrac{ x^2-4}{x^2+2x-15 } \)
    1. \( f(x) = \dfrac{x^2-x }{ x^2+7x+10} \)
    2. \( f(x) = \dfrac{x^2+4x+3 }{ x^2-5x+4} \)
    3. \( f(x) = \dfrac{x^3-x^2-x+1 }{ 2x^2-11x+12} \)
    4. \( f(x) = \dfrac{x^3-2x^2-x+2 }{ 3x^2-11x+6} \\[6pt] \)
    1. \( f(x) = \dfrac{x-1 }{x^2-7x+10 } \)
    2. \( f(x) = \dfrac{ x+2}{x^2+x-12 } \)
    3. \( f(x) = \dfrac{ x^2-1}{x^3-x^2-4x+4 } \)
    4. \( f(x) = \dfrac{ x^2+7x+12}{ x^3+9x^2+20x} \)
    1. \( f(x) = \dfrac{x^2+4x+3 }{x^2+6x+8 } \)
    2. \( f(x) = \dfrac{ x^2-2x-3}{x^2+2x } \)
    3. \( f(x) = \dfrac{ x-3}{ x^2+x-2} \)
    4. \( f(x) = \dfrac{x^2-6x+9 }{x^2+x-6 } \)
    1. \( f(x) = \dfrac{ x^2+x-12}{ x^2-4} \)
    2. \( f(x) = \dfrac{ x-3}{x^3-2x^2-4x+8 } \)
    3. \( f(x) = \dfrac{ (x^3+3x^2+9x)}{ x^2+x-2} \)
    4. \( f(x) = \dfrac{x^4+x^2 }{x^3-4x } \)
    Answers to odd exercises #51-67. More graphs at the end of this section

    51. \(\left(\frac{3}{2}, \infty\right)\)

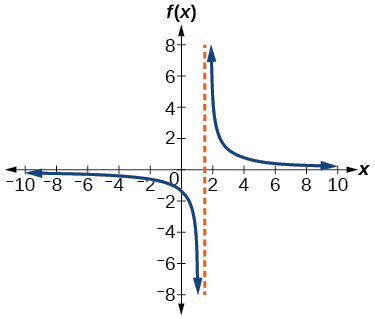
    CNX_Precalc_Figure_03_07_226.jpg

    53. V.A. \(x=-4\), H.A. \(y=2\); \(\left(\frac{3}{2}, 0\right)\); \(\left(0,-\frac{3}{4}\right)\)

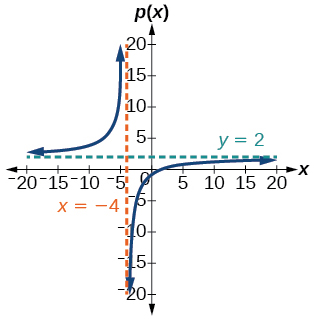
    CNX_Precalc_Figure_03_07_205.jpg

    55. V.A. \(x=2\), H.A. \(y=0\), \((0,1)\)

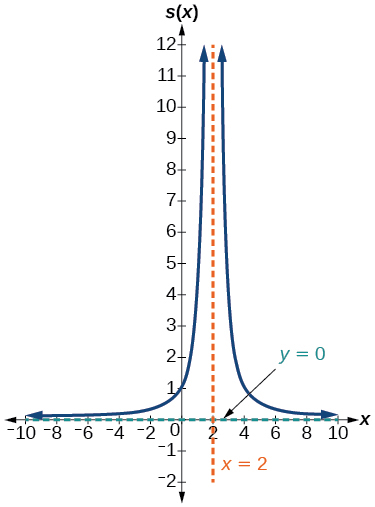
    CNX_Precalc_Figure_03_07_207.jpg 

    57. \((-2,1) \cup(4, \infty)\)

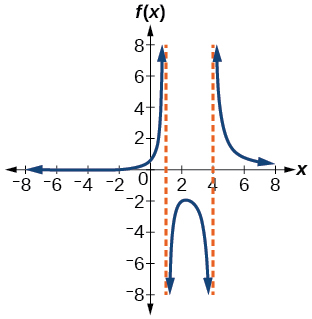
    CNX_Precalc_Figure_03_07_228.jpg 

    59. 
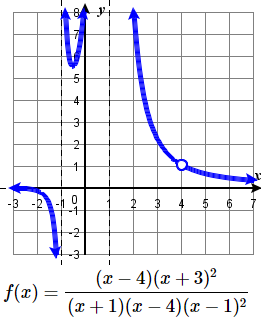
     3.9e #59.png

    61.

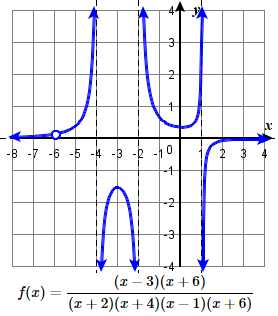
     3.9e #61.png 

    63. V.A. \(x=-4\), \(x=\frac{4}{3}\), H.A. \(y=1\); \((5,0)\); \(\left(-\frac{1}{3}, 0\right)\); \(\left(0, \frac{5}{16}\right)\)

    CNX_Precalc_Figure_03_07_209.jpg 

    65. V.A. \(x=−1\), H.A. \(y=1\); \((−3,0)\); \((0,3)\)

    CNX_Precalc_Figure_03_07_211.jpg 

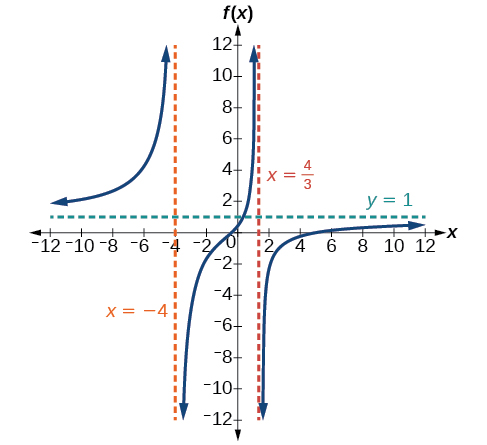
    67. V.A. \(x=4\), S.A. \(y=2x+9\); \((-1,0)\); \(\left(\frac{1}{2}, 0\right)\); \(\left(0, \frac{1}{4}\right)\)

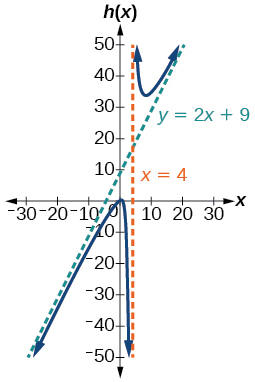
    CNX_Precalc_Figure_03_07_213.jpg 

    H: Construct an Equation from a Description

    Exercise \(\PageIndex{H}\)

    \( \bigstar \) Write an equation for a rational function with the given characteristics.

    1. Vertical asymptotes at \(x=5\) and \(x=-5\), \(x\)-intercepts at \((2,0)\) and \((-1,0)\) , \(y\) -intercept at \((0,4)\)
    2. Vertical asymptotes at \(x=-4\) and \(x=-1, x\) -intercepts at \((1,0)\) and \((5,0), y\) -intercept at \((0,7)\)
    3. Vertical asymptotes at \(x=-4\) and \(x=-5, x\) -intercepts at \((4,0)\) and \((-6,0),\) Horizontal asymptote at \(y=7\)
    4. Vertical asymptotes at \(x=-3\) and \(x=6, x\) -intercepts at \((-2,0)\) and \((1,0),\) Horizontal asymptote at \(y=-2\)
    5. Vertical asymptote at \(x=-1,\) Double zero at \(x=2, y\) -intercept at \((0,2)\)
    6. Vertical asymptote at \(x=3,\) Double zero at \(x=1, y\) -intercept at \((0,4)\)
    Answers to odd exercises.

    105. \(y=\dfrac{50(x-2)(x+1)}{(x-5)(x+5)}\) \(\quad \) 107. \(y=\dfrac{7(x+6)(x-4)}{(x+5)(x+4)}\) \(\quad \) 109. \(y=\dfrac{(x-2)^2}{2(x+1)}\) 

    I: Construct an Equation from a Graph

    Exercise \(\PageIndex{I}\)

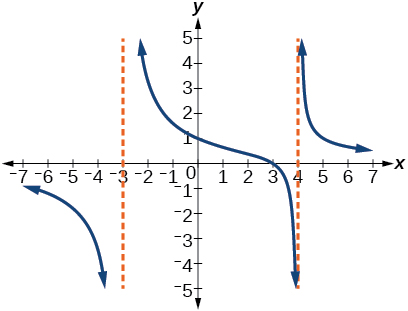
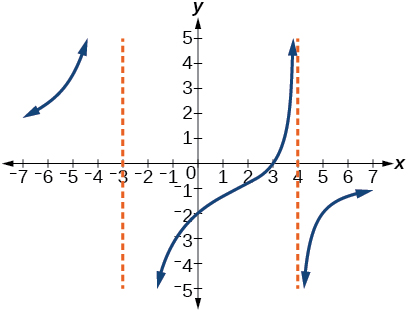
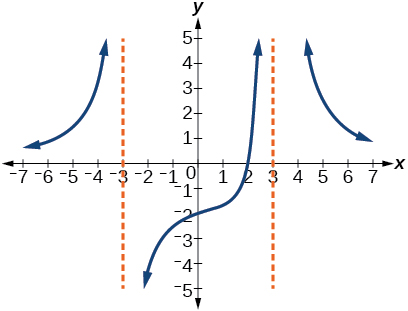
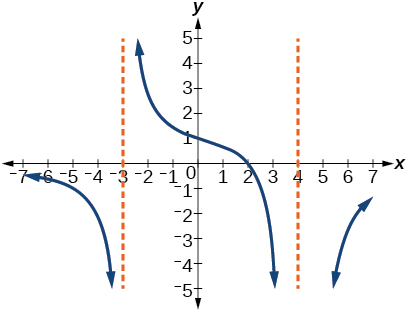
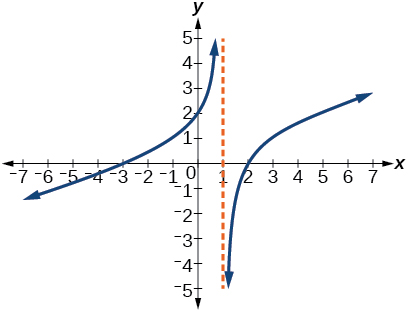
    \( \bigstar \) Use the graphs to write an equation for the function.

    111.

    CNX_Precalc_Figure_03_07_217.jpg 

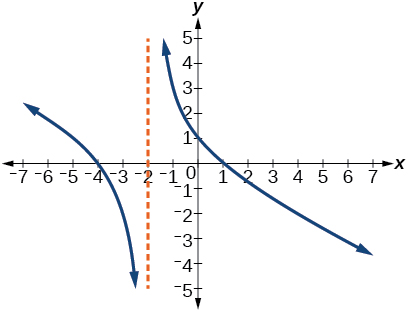
    112.

    CNX_Precalc_Figure_03_07_218.jpg 

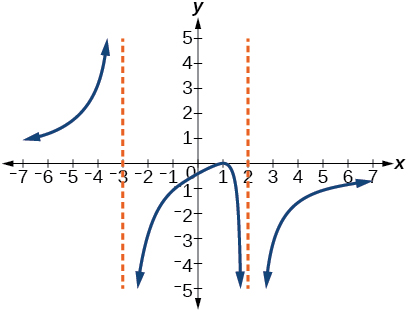
    113.

    CNX_Precalc_Figure_03_07_219.jpg 

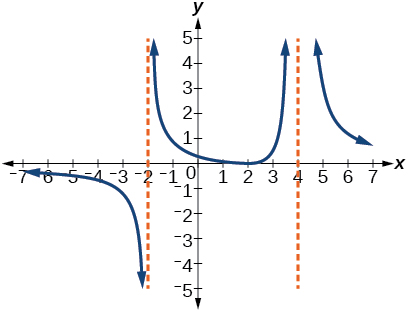
    114.

    CNX_Precalc_Figure_03_07_220.jpg 

    115.

    CNX_Precalc_Figure_03_07_221.jpg 

    116.

    CNX_Precalc_Figure_03_07_222.jpg 

    117.

    CNX_Precalc_Figure_03_07_223.jpg 

    118.

    CNX_Precalc_Figure_03_07_224.jpg 

    		  
    Answers to odd exercises.

    111. \(y= \dfrac{4(x-3)}{(x-4)(x+3)}\) \(\quad \) 113. \(y= \dfrac{27(x-2)}{(x+3)(x-3)^2}\) \(\quad \) 

    115. \(y=\dfrac{(x+3)(x-2)}{3(x-1)}\) \(\quad \) 117. \(y=\dfrac{-6(x-1)^{2}}{(x+3)(x-2)^{2}}\) 

    J: Use tables to show behaviour

    Exercise \(\PageIndex{J}\)

    \( \bigstar \) Make tables to show the behavior of the function near the vertical asymptote and horizontal asymptote

    1. \(f(x)=\dfrac{1}{x-2}\)
    1. \(f(x)=\dfrac{x}{x-3}\)
    1. \(f(x)=\dfrac{2x}{x+4}\)
    1. \(f(x)=\dfrac{2 x}{(x-3)^{2}}\)
    1. \(f(x)=\dfrac{x^{2}}{x^{2}+2 x+1}\)
    Answers to odd exercises.
    121.
    Vertical asymptote \(x=2\)
    2.01 2.001 2.0001 1.99 1.999
    100 1,000 10,000 –100 –1,000
    Horizontal asymptote \( y=0\)
    10 100 1,000 10,000 100,000
    .125 .0102 .001 .0001 .00001

    123. 
    Vertical asymptote \(x=-4\)
    –4.1 –4.01 –4.001 –3.99 –3.999
    82 802 8,002 –798 –7998
    Horizontal asymptote \(y=2 \)
    10 100 1,000 10,000 100,000
    1.4286 1.9331 1.992 1.9992 1.999992

    125.
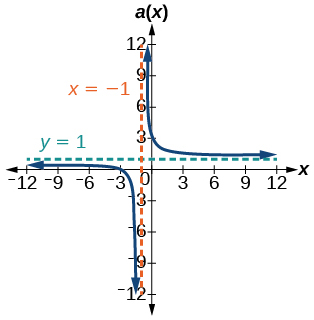
    Vertical asymptote \(x=-1\)
    –.9 –.99 –.999 –1.1 –1.01
    81 9,801 998,001 121 10,201
    Horizontal asymptote \(y=1\)
    10 100 1,000 10,000 100,000
    .82645 .9803 .998 .9998 .99998
     

    G: Additional Answers for section G (#71-101)

    Exercise \(\PageIndex{A}\)

     Graphs of odd-numbered exercises #71-101 in section G

    Additional answers to odd exercises.

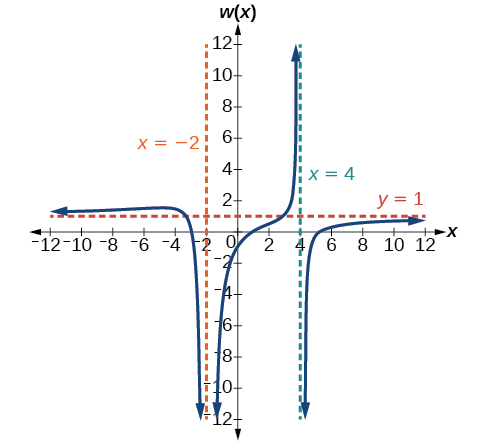
    69. V.A. \(x=-2\), \(x=4\), H.A. \(y=1\), \((1,0)\); \((5,0)\); \((-3,0)\); \(\left(0,-\frac{15}{16}\right)\)

    CNX_Precalc_Figure_03_07_215.jpg 

    		 71. 
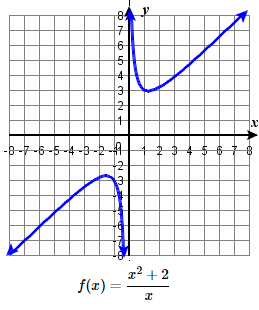
    3.9e #71.png    		 73. 
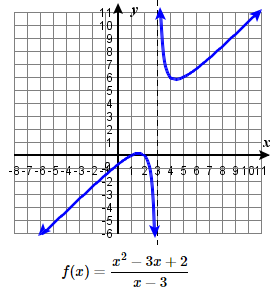
    3.9e #73.png
    75. 
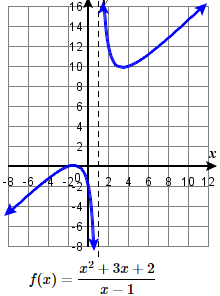
    3.9e #75.png     		 77. 
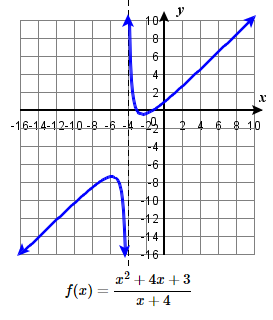
    3.9e #77.png    		 79. 
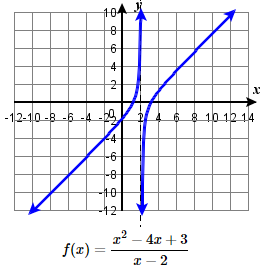
    3.9e #79.png
    81. 
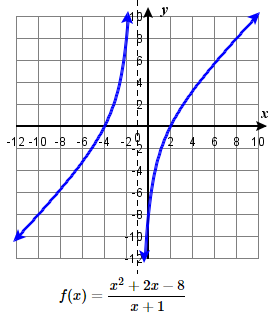
    3.9e #81.png     		 83. 
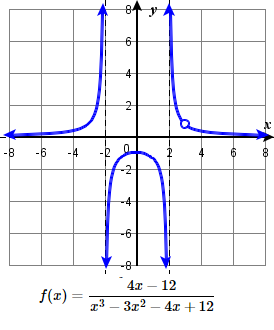
    3.9e #83.png    		 85. 
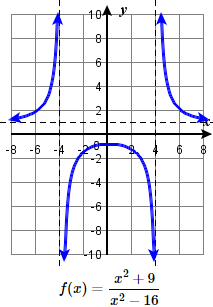
    3.9e #85.png
    87. 
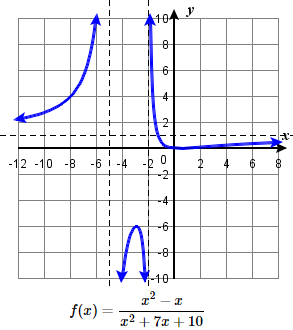
    3.9e #87.png     		 89. 
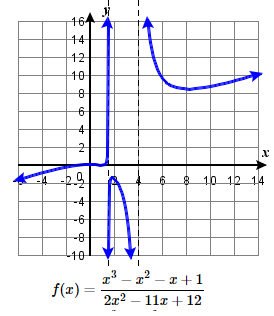
    3.9e #89.png    		 91. 
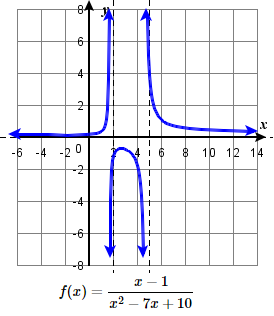
    3.9e #91.png
    93. 
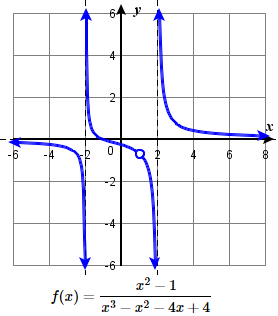
    3.9e #93.png    		 95. 
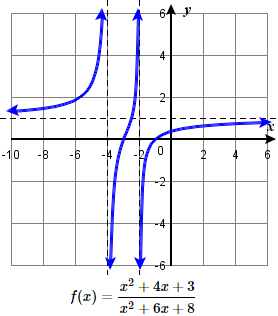
    3.9e #95.png    		 97. 
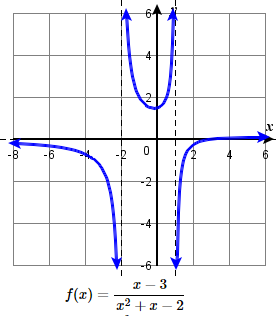
    3.9e #97.png
    99. 
    3.9e #99.png     		 101. 
    3.9e #101.png     		  

    \( \bigstar \)

     

    This page titled 3.9e: Exercises - Rational Functions is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      OpenStax
      License
      CC BY
      License Version
      4.0
    2. Tags
      This page has no tags.