5.3: Sine and Cosine Functions
- Page ID
- 34915
Learning Objectives
- Define the sine and cosine functions
- Find function values for the sine and cosine of 30° or \((\tfrac{\pi}{6}),\) 45° or \((\tfrac{\pi}{4})\), and 60° or \((\tfrac{\pi}{3})\).
- Find reference angles.
- Use reference angles to evaluate trigonometric functions.
While it is convenient to describe the location of a point on a circle using the radius of the circle and the measure of a central angle in the circle, relating this information to \(x\) and \(y\) coordinates is an important application of trigonometry.
An example of a problem that can be solved using the techniques of this section follows: A distress signal is sent from a sailboat during a storm, but the transmission is unclear and the rescue boat sitting at the marina cannot determine the sailboat’s location. Using high powered radar, they determine the distress signal is coming from a distance of 20 miles at an angle of 225 degrees from the marina. How many miles east/west and north/south of the rescue boat is the stranded sailboat?
Reference Triangles
We begin by drawing a circle centered at the origin with radius \(r\), and marking the point on the circle indicated by some angle \(\theta\). This point has coordinates (\(x\), \(y\)).
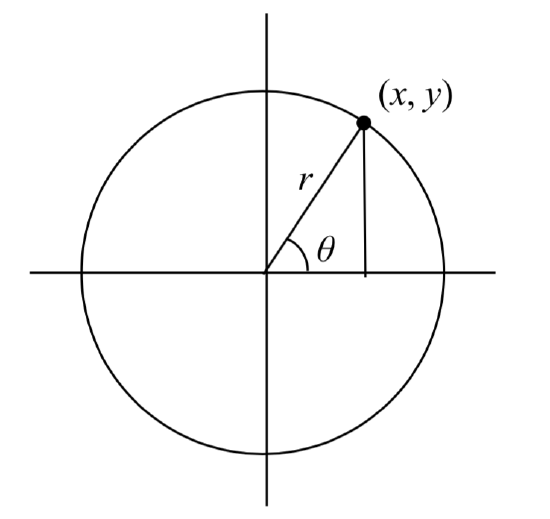
Definition: reference triangle
A reference triangle is the right triangle inside a circle formed by dropping a perpendicular line segment to the \(x\)-axis from a point \( (x, y) \) on the terminal side of an angle in standard position that has its vertex in the center of a circle of radius \(r\). The positive acute angle between the \(x\)-axis and the terminal side of the angle \( \theta \) is the reference angle.
Some important points about this are made here.
- No matter which quadrant our angle \(\theta\) puts us in, we can draw a triangle by dropping a perpendicular line segment to the \(x\) axis. The values of \(x\) and \(y\) may be positive or negative, depending on the quadrant the terminal side is in. The value of \(r\) is always positive.
- If the angle \(\theta\) puts us on an axis, we simply measure the radius as the magnitude of an \(x\) or \(y\) value on the axis, with the other value being 0, again ensuring we have appropriate signs on the coordinates based on the axis the point is on.
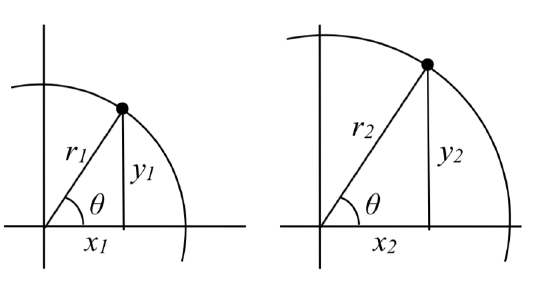
- Triangles obtained from different radii will all be similar triangles, meaning corresponding sides scale proportionally. While the lengths of the sides may change, the ratios of the side lengths will always remain constant for any given angle. Thus,
\( \dfrac{y_{1} }{r_{1} } =\dfrac{y_{2} }{r_{2} } \qquad \dfrac{x_{1} }{r_{1} } =\dfrac{x_{2} }{r_{2} }\)
To be able to refer to these ratios more easily, we will give them names. Since the ratios depend on the angle, we will write them as functions of the angle \(\theta\).
Sine and Cosine Function Values
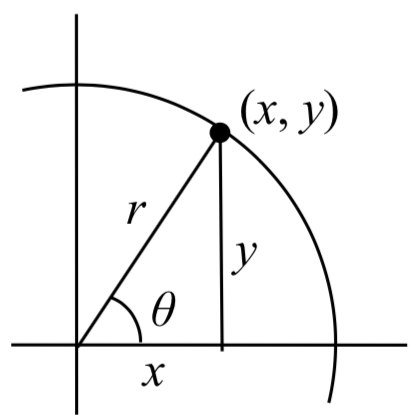
Definition: sine and cosine
For the point (\(x\), \(y\)) on a circle of radius \(r\) at an angle of \(\theta\) in standard position, we can define two important functions as the ratios of the sides of the corresponding triangle:
The sine function: \(\sin (\theta )=\dfrac{y}{r}\)
The cosine function: \(\cos (\theta )=\dfrac{x}{r}\)
Note that the definition of the sine and cosine functions depends on the values of a point \( (x, y) \) on the terminal side of the angle. Consequently
- The point chosen can be ANY point on the terminal side of an angle in standard position.
- The sign of the ratio obtained depends on the signs of the point \( (x, y) \), which in turn is determined by the quadrant the angle is in.
|
The value of the radius \(r\) of a circle is ALWAYS positive. Therefore, the sign of a sine or cosine function is entirely determined by the signs of \(x\) and \(y\) for a point on the terminal side of the angle. |
\( \sin \theta =\dfrac{y}{r} \) \( \begin{array}{c|c} Sine is positive when the terminal side |
\( \cos \theta =\dfrac{x}{r} \) \( \begin{array}{c|c} Cosine is positive when the terminal side |
In this chapter, we will explore these functions using both circles and right triangles.
Using a Point on the Terminal Side of an Angle
The definition of the sine and cosine functions depends on the coordinates of a point on the terminal side of an angle in standard position. In order to find the sine and cosine function values, this point can be given to us. Alternatively, if we are given an angle with a terminal side on one of the axes, the point can be chosen by us.
Example \(\PageIndex{1}\): Find sine and cosine given a point on the terminal side of an angle
The point (3, 4) is on the circle of radius 5 at some angle \(\theta\). Find \(\cos (\theta )\)and \(\sin (\theta )\).
Solution
Knowing the radius of the circle and coordinates of the point, we can evaluate the cosine and sine functions as the ratio of the sides.
\[\cos (\theta )=\dfrac{x}{r} =\dfrac{3}{5} \qquad \qquad \sin (\theta )=\dfrac{y}{r} =\dfrac{4}{5}\nonumber\]
There are a few cosine and sine values which we can determine fairly easily because the corresponding point on the terminal side falls on the \(x\) or \(y\) axis.
Example \(\PageIndex{2}\): Find sine and cosine of a quadrantal angle
Find \(\cos (90{}^\circ )\) and \(\sin (90{}^\circ )\).
Solution
The terminal side of a 90 degree angle in standard position points straight up, so the coordinates of the corresponding point on the circle would be (0, r). Using our definitions of cosine and sine,
\(\cos (90{}^\circ )=\dfrac{x}{r} =\dfrac{0}{r} =0\) \( \quad \) \(\sin (90{}^\circ )=\dfrac{y}{r} =\dfrac{r}{r} =1\)
![]() Try It \(\PageIndex{2}\)
Try It \(\PageIndex{2}\)
Find cosine and sine of the angle \(\pi\).
- Answer
- \(\cos (\pi )=-1 \quad \sin (\pi )=0\)
Given a Trigonometric Ratio and the Quadrant the Angle is in
Use a Reference Triangle
Given one trigonometric ratio and the quadrant where the terminal side lies, the Pythagorean Theorem can be used to find a corresponding third side to the triangle, and then other trigonometric ratios can be determined.
![]() How to: Use a Reference Triangle to find sine or cosine given the other ratio and the quadrant the angle is in.
How to: Use a Reference Triangle to find sine or cosine given the other ratio and the quadrant the angle is in.
Method #1: Reference Triangle Approach. Given a trigonometric ratio and the quadrant the terminal side of the angle is in.
- Use the definition of the given trigonometric function and the quadrant it is in to determine two of the three sides of a reference triangle ( \(x,\) \(y,\) and \(r\)). Depending on the quadrant the angle is in, \(x\) or \(y\) can be negative.
- Use the Pythagorean Theorem to find the third side
- Choose the solution with the sign that is appropriate to the Quadrant the angle is in. Now that all three sides of a reference triangle for the angle are known, use the definitions to determine the other trigonometric ratio.
Example \(\PageIndex{3}\)
Given \( \sin(\theta) = -\dfrac{4}{11} \) and \(\theta\) is in Quadrant III, find \(\cos (\theta)\).
Solution (Method #1: Reference Triangle Approach)
1. Since \(\sin (\theta )= -\dfrac{4}{11}=\dfrac{y}{r}\) and \(r\) is always positive, we can conclude \(y=-4\) and \(r=11\)
2. By the Theorem of Pythagoras, \(x^2+y^2 = r^2.\) Substituting the known values from step one we have
\(\begin{align*} x^2+(-4)^2 &= (11)^2\\
x^2+16 &= 121\\
x^2 &= 105\\
x&=±\sqrt{105}
\end{align*}\)
3. Because \(\theta\) is in Quadrant III where \(x\) coordinates are always negative, \(x=-\sqrt{105}\).
\(\quad\)The definition for cosine is \(\cos (\theta )=\dfrac{x}{r}.\) Substituting the values we have for \(x\) and \(r\) we have \(\cos (\theta )=\dfrac{-\sqrt{105}}{11}\).
Use The Pythagorean Identity
The basic equation for a circle centered at the origin is \(x^{2} +y^{2} =r^{2}.\) Combine this with the definition for sine and cosine above, to establish a new identity.
\( \begin{array}{rll}
x^2 +y^2 &=r^2 & \text{Start with equation for a circle} \\
\dfrac{x^2 +y^2}{r^2} &=\dfrac{r^2}{r^2} & \text{Divide through by } r^2 \\
\dfrac{x^2}{r^2} +\dfrac{y^2}{r^2} &=1 & \text{Rewrite } \\
\left( \dfrac{x}{r} \right)^2+\left( \dfrac{y}{r} \right)^2 &=1 & \text{Rewrite } \\
(\cos (\theta ))^2 +(\sin (\theta ))^2 &=1 & \text{Substitute the definitions above} \\
\cos ^2 (\theta )+\sin ^2 (\theta ) &=1 & \text{Rewrite} \\
\end{array} \)
Here \(\cos ^{2} (\theta )\) is a commonly used shorthand notation for \((\cos (\theta ))^{2}\). Be aware that many calculators and computers do not understand the shorthand notation.
Definition: Pythagorean Identity
The Pythagorean Identity. For any angle \(\theta\), \[\cos ^{2} (\theta )+\sin ^{2} (\theta )=1\nonumber\]
One use of this identity is that it helps us to find a cosine value of an angle if we know the sine value of that angle or vice versa. However, since the equation will yield two possible values, we will need to utilize additional knowledge of the Quadrant the angle is in to help us find the desired value.
![]() How to: Use Identities to find sine or cosine given the other ratio and the quadrant the angle is in.
How to: Use Identities to find sine or cosine given the other ratio and the quadrant the angle is in.
Method #2: Identities Approach. Given a trigonometric ratio and the quadrant the terminal side of the angle is in.
- Use the Pythagorean Identity to determine the sine or cosine ratio of an angle from the other ratio that was given.
- Choose the solution with the sign that is appropriate to the Quadrant the angle is in.
Example \(\PageIndex{4}\)
If \(\sin (\theta )=\dfrac{3}{7}\) and \(\theta\) is in the second quadrant, find \(\cos (\theta )\).
Solution (Method #2: Identities Approach)
Substitute the known value for sine into the Pythagorean identity,
\( \begin{array}{rll}
\cos ^{2} (\theta )+\sin ^{2} (\theta ) &=1 & \text{Pythagorean Identity}\\
\cos ^{2} (\theta )+\dfrac{9}{49} &=1 & \text{Substitute given values} \\
\cos ^{2} (\theta ) &=1 - \dfrac{9}{49} \\
\cos ^{2} (\theta ) &=\dfrac{40}{49} \\
\cos (\theta ) &=\pm \sqrt{\dfrac{40}{49} } =\pm \dfrac{\sqrt{40} }{7} \\
&=\pm \dfrac{2\sqrt{10} }{7} \\
\end{array} \)
Since we are given that \(\theta\) is in the second quadrant, \(x\) coordinates of points in Quadrant II are negative, and \(\cos (\theta )=\dfrac{x}{r}\), we can conclude the cosine value is also be negative. Therefore, \(\cos (\theta ) = -\dfrac{2\sqrt{10} }{7}\)
![]() Try It \(\PageIndex{4}\)
Try It \(\PageIndex{4}\)
If \(\cos (\theta)=\dfrac{24}{25}\) and \(\theta\) is in the fourth quadrant, find \( \sin (\theta)\).
- Answer
-
\(\sin (\theta)=−\dfrac{7}{25}\)
Sines and Cosines of Special Angles
Using the Pythagorean Identity and some knowledge about triangles, values for the sine and cosine of some special angles can be determined.
45° or π/4 Angles
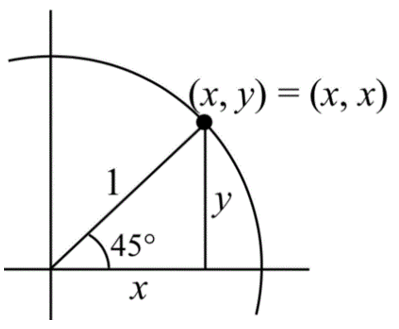
First, consider a point on a circle at an angle of 45°, or \(\dfrac{\pi }{4}\). At this angle, the x and y coordinates of the corresponding point on the circle will be equal because 45° divides the first quadrant in half. Since the \(x\) and \(y\) values will be the same, the sine and cosine values will also be equal. Utilizing the Pythagorean Identity,
\( \begin{array}{rll}
\cos ^{2} \left(\dfrac{\pi }{4} \right)+\sin ^{2} \left(\dfrac{\pi }{4} \right) &=1 &\text{since the sine and cosine are equal} \\
\cos ^{2} \left(\dfrac{\pi }{4} \right)+\cos ^{2} \left(\dfrac{\pi }{4} \right) &=1 &\text{add like terms} \\
2\cos ^{2} \left(\dfrac{\pi }{4} \right) &=1 &\text{divide} \\
\cos ^{2} \left(\dfrac{\pi }{4} \right) &=\dfrac{1}{2} &\text{since the \(x\) value is positive} \\
\cos \left(\dfrac{\pi }{4} \right) &=\sqrt{\dfrac{1}{2} } &\text{rationalize the denominator} \\
\cos \left(\dfrac{\pi }{4} \right) &=\dfrac{\sqrt{2} }{2} &\text{Because }=\sqrt{\dfrac{1}{2} } \sqrt{\dfrac{2}{2} } =\sqrt{\dfrac{2}{4} }
\end{array} \)
Since the sine and cosine are equal, \(\sin \left(\dfrac{\pi }{4} \right)=\dfrac{\sqrt{2} }{2}\) as well. The (\(x\), \(y\)) coordinates for a point on a circle of radius 1 at an angle of 45° are \(\left(\dfrac{\sqrt{2} }{2} ,\dfrac{\sqrt{2} }{2} \right)\).
30° or π/6 Angles
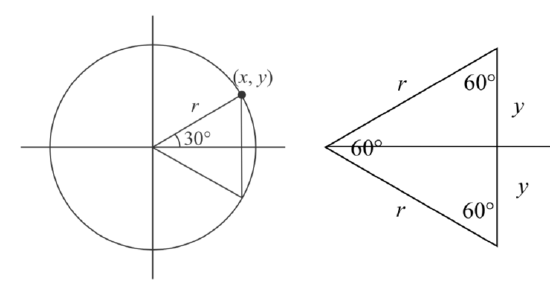
Next, we will find the cosine and sine at an angle of 30°, or \(\frac{\pi }{6}\). To do this, we will first draw a triangle inside a circle with one side at an angle of 30°, and another at an angle of -30°. If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be 60°.
Since all the angles are equal, the sides will all be equal as well. The vertical line has length \(2y\), and since the sides are all equal we can conclude that \(2y = r\), or \(y=\dfrac{r}{2}\). Using this, we can find the sine value:
\[\text{sin}\left(\dfrac{\pi}{6}\right) = \dfrac{y}{r} = \dfrac{r/2}{r} = \dfrac{r}{2} \cdot \dfrac{1}{r} = \dfrac{1}{2}\nonumber\]
Using the Pythagorean Identity, we can find the cosine value:
\(\cos ^{2} \left(\dfrac{\pi }{6} \right)+\sin ^{2} \left(\dfrac{\pi }{6} \right)=1\)
\(\cos ^{2} \left(\dfrac{\pi }{6} \right)+\left(\dfrac{1}{2} \right)^{2} =1\)
\(\cos ^{2} \left(\dfrac{\pi }{6} \right)=\dfrac{3}{4}\)
since the \(x\) value is positive, we’ll keep the positive root
\(\cos \left(\dfrac{\pi }{6} \right)=\sqrt{\dfrac{3}{4} } =\dfrac{\sqrt{3} }{2}\)
The (\(x\), \(y\)) coordinates for the point on a circle of radius 1 at an angle of 30 degrees are \(\left(\dfrac{\sqrt{3} }{2} ,\dfrac{1}{2} \right)\).
60° or π/3 Angles
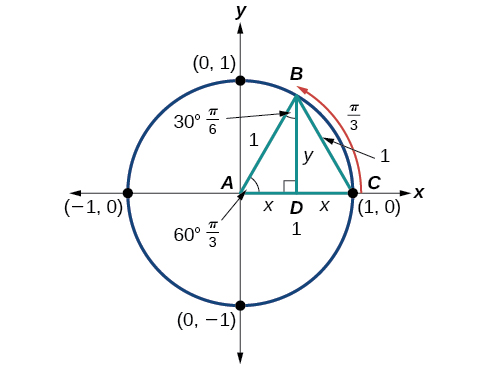
Consider an equilateral triangle \(ABC\) inscribed in a circle of radius \(1\) below. All angles in this triangle are 60° so Angle \(A\) has measure 60°. Construct \(BD\) that bisects angle \(B\). Therefore \(BD\) is the perpendicular bisector of \(AC\), so it cuts \(AC\) in half, which means that \(AD\) is \( \dfrac{1}{2}\) the radius, or \(x = \dfrac{1}{2}.\)
\(\begin{array}{rl}
x^2+y^2 &=1 &\text{From the Pythagorean Theorem } \\
\left( \dfrac{1}{2} \right)^2+y^2 &=1 &\text{Because \(x\) is \( \frac{1}{2}\) the radius is }1 \\
y^2 &=1−\dfrac{1}{4} &\text{Solve for \(y\) } \\
y^2 &= \dfrac{3}{4} \\
y &=± \dfrac{\sqrt{3}}{2} \\
y &=\dfrac{\sqrt{3}}{2} &\text{in QI where \(x\) and \(y\) are positive } \\
\end{array}\)
Thus, \( \sin \left(\dfrac{\pi }{3} \right)=\dfrac{y}{r} =\dfrac{\sqrt{3} }{2}\) and \(\cos \left(\dfrac{\pi }{3} \right)=\dfrac{x}{r} =\dfrac{1}{2}\)
The \((x,y)\) coordinates for the point on a circle of radius \(1\) at an angle of \(60°\) are \(\left(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)\)
Summary
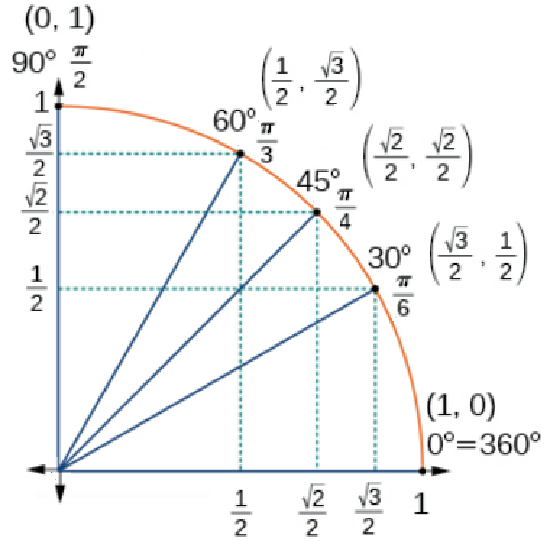
We have now found the cosine and sine values for all the commonly encountered angles that have their terminal side in the first quadrant. This information is summarized below in both a table format and in a diagram of the first quadrant of the unit circle. These values for sine and cosine should be thoroughly memorized.
| Angle | 0 or 0° | \(\dfrac{π}{6}\) or 30° | \(\dfrac{π}{4}\) or 45° | \(\dfrac{π}{3}\) or 60° | \(\dfrac{π}{2}\) or 90° |
|---|---|---|---|---|---|
| Sine | 0 | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | 1 |
| Cosine | 1 | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | 0 |
Reference Angles
Definition: Reference Angles
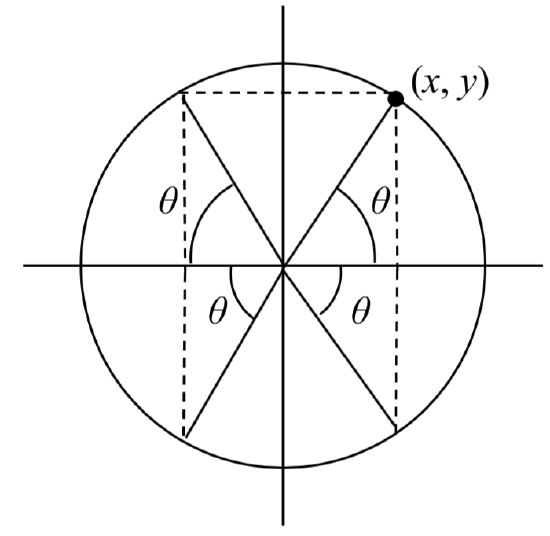 An angle’s reference angle is the measure of the smallest, positive, acute angle \(\theta\) formed by the terminal side of the angle \(\theta\) and the horizontal axis. It is the acute angle located at the origin of a reference triangle.
An angle’s reference angle is the measure of the smallest, positive, acute angle \(\theta\) formed by the terminal side of the angle \(\theta\) and the horizontal axis. It is the acute angle located at the origin of a reference triangle.
The diagram to the right illustrates the reference angle \(\theta\) for angles in standard position that have a terminal side in one of the four quadrants. Notice the reference angle is NOT in standard position (except in Quadrant I)
A reference angle is always an angle between 0° and 90°, or 0 and \(\dfrac{\pi }{2}\) radians.
Any reference angle in standard position is always in Quadrant I. Consequently, all trigonometric ratios for a reference angle are never negative.
Reference angles are always between 0 and \(\dfrac{\pi }{2}\), so the sine and cosine values for reference angles will never be negative. Angles with the same reference angles all have the same cosine and sine values, except possibly for their sign (positive or negative). The sign of the sine or cosine ratio is determined by which quadrant the angle is in.
Angles with the Same Sine or Cosine
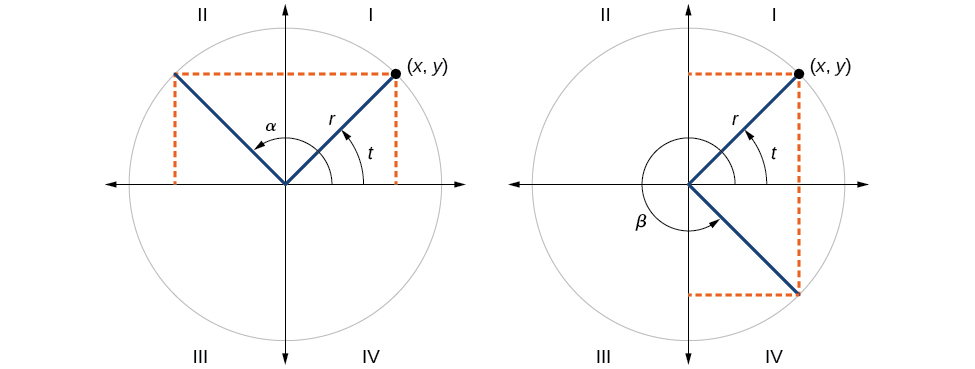
\(\qquad \qquad \)In QIV, \( \sin(t) = -\sin(β)\) and \( \cos(t) = \cos(β) \)
Any angle in the first quadrant is a reference angle. Any point \((x, \; y)\) on the terminal side of this angle has \(x\) and \(y\) coordinates that are both positive.
For any given angle in the first quadrant, there is an angle in the second quadrant with the same sine value because the sine value is the ratio \(\frac{y}{r}\), and \(y\) coordinates are positive in Quadrant I and Quadrant II. However, this angle in Quadrant II with the same positive \(y\)-value, will have the opposite (i.e. negative) value for \(x\). Thus although the sine is the same, the cosine for the angle in Quadrant II will be negative.
Likewise, there will be an angle in the fourth quadrant with the same cosine as the original (reference) angle. The angle with the same cosine will share the same \(x\)-value but will have the opposite \(y\)-value. Therefore, its sine value will be the opposite of the original angle’s sine value. This is illustrated in Figure \(\PageIndex{5}\).
Finding a Reference Angle
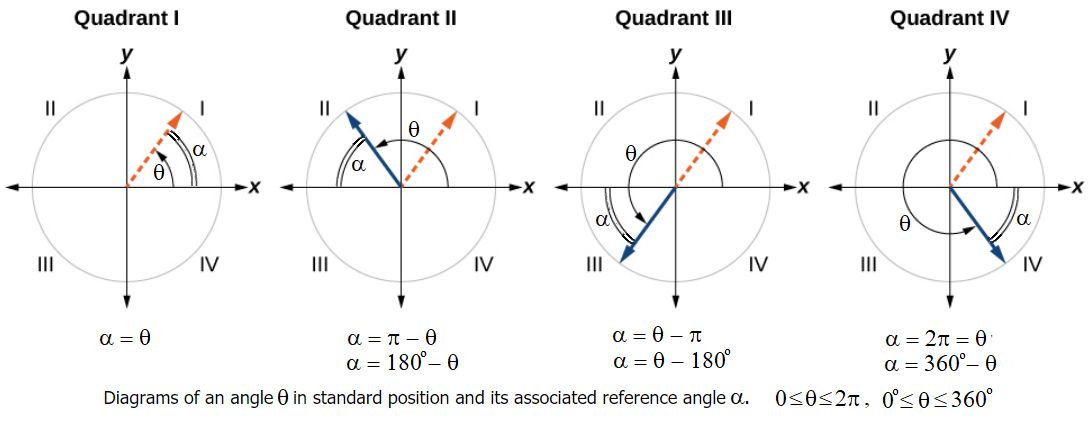
Recall that an angle’s reference angle is the acute angle, \( \alpha\), formed by the terminal side of the angle \( \theta \) and the horizontal axis. A reference angle is always an angle between \(0\) and \(90°\), or \(0\) and \(\dfrac{π}{2}\) radians and it is not in standard position (except in QI). As we can see from Figure \(\PageIndex{6}\), for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.
![]() Howto: Find a reference angle.
Howto: Find a reference angle.
- Given an angle \(\theta\), if the angle is in degrees and not in the interval \( [0^{\circ}, 360^{\circ})\), or if the angle is in radians and not in the interval \( [0,2π)\), find a coterminal angle that is in these intervals (by adding or subtracting \(360^{\circ}\) or \(2π\) ) .
- An angle in the first quadrant is its own reference angle.
- For an angle in the second or third quadrant, the reference angle is \(|π−\theta|\) or \(|180°−\theta|\).
- For an angle in the fourth quadrant, the reference angle is \(2π−\theta\) or \(360°−\theta.\)
Example \(\PageIndex{6}\): Find a Reference Angle
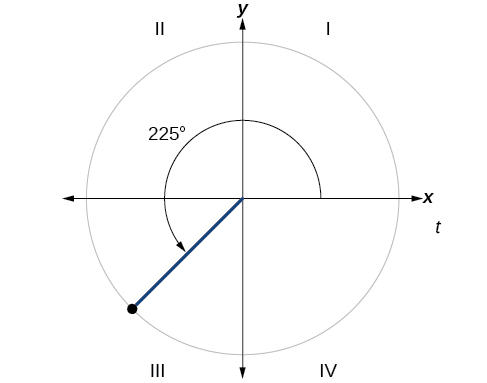
Find the reference angle for \(225°\) as shown in Figure \(\PageIndex{7}\).
Solution
Because \( 225°\) is in the third quadrant, the reference angle is \(|(180°−225°)|=|−45°|=45° \)
![]() Try It \(\PageIndex{6}\)
Try It \(\PageIndex{6}\)
Find the reference angle for \(\frac{5π}{3}\).
- Answer
-
\(\dfrac{π}{3}\)
The reader may have noticed that when expressed in radian measure, the reference angle for a non-quadrantal angle is easy to spot. Reduced fraction multiples of \(\pi\) with a denominator of \(6\) have \(\frac{\pi}{6}\) as a reference angle, those with a denominator of \(4\) have \(\frac{\pi}{4}\) as their reference angle, and those with a denominator of \(3\) have \(\frac{\pi}{3}\) as their reference angle.
Use Reference Angles to Evaluate Trigonometric Functions
We can find the cosine and sine of any angle in any quadrant if we know the cosine or sine of its reference angle. The absolute values of the cosine and sine of an angle are the same as those of the reference angle. The sign depends on the quadrant of the original angle. The cosine will be positive or negative depending on the sign of the \(x\)-values in that quadrant. The sine will be positive or negative depending on the sign of the \(y\)-values in that quadrant.
Reference Angle Theorem
Angles have cosines and sines with the same absolute value as cosines and sines of their reference angles. The sign (positive or negative) can be determined from the quadrant of the angle.
Suppose \(\alpha\) is the reference angle for \(\theta\). Then \(\cos(\theta) = \pm \cos(\alpha)\) and \(\sin(\theta) = \pm \sin(\alpha)\), where the choice of the (\(\pm\)) depends on the quadrant in which the terminal side of \(\theta\) lies.
![]() Howto: Use reference angles to find the sine or cosine of an angle.
Howto: Use reference angles to find the sine or cosine of an angle.
- Measure the angle between the terminal side of the given angle and the horizontal axis. That is the reference angle.
- Determine the values of the cosine and sine of the reference angle.
- Give the cosine the same sign as the \(x\)-values in the quadrant of the original (given) angle.
- Give the sine the same sign as the \(y\)-values in the quadrant of the original (given) angle.
Example \(\PageIndex{7}\): Use Reference Angles to Find the Sine and Cosine for Multiples of Special Angles
- Use a reference angle to find the exact value of \(\cos (150°)\) and \( \sin (150°)\).
- Use a reference angle to find \( \cos \dfrac{5π}{4}\) and \(\sin \dfrac{5π}{4}\).
a. Solution
- The reference angle for 150° is 30°
- \( \cos 30° = \dfrac{\sqrt{3}}{2}\) and \( \sin 30° = \dfrac{\sqrt{3}}{2}\)
- Since \(150°\) is in the second quadrant, the \(x\)-coordinate of the point on the circle is negative, so the cosine value is negative. Thus, \( \cos 150° = -\dfrac{\sqrt{3}}{2}\)
- Since \(150°\) is in the second quadrant, the \(y\)-coordinate of the point on the circle is positive, so the sine value is positive. Thus, \( \sin 150° = \dfrac{1}{2}\).
b. Solution
- The reference angle for \(\dfrac{5π}{4}\) is \(\dfrac{π}{4}\)
- \( \cos \dfrac{π}{4} = \dfrac{\sqrt{2}}{2}\) and \( \sin\dfrac{π}{4} = \dfrac{\sqrt{2}}{2}\)
- Since \(\dfrac{5π}{4}\) is in the third quadrant, the \(x\)-coordinate of the point on the circle is negative, so the cosine value is negative. Thus, \( \cos \dfrac{5π}{4} = -\dfrac{\sqrt{2}}{2}\)
- Since \(\dfrac{5π}{4}\) is in the third quadrant, the \(y\)-coordinate of the point on the circle is negative, so the sine value is negative. Thus, \( \sin \dfrac{5π}{4} = - \dfrac{\sqrt{2}}{2}\).
![]() Try It \(\PageIndex{7}\)
Try It \(\PageIndex{7}\)
- Use the reference angle for \(315°\) to find \( \cos (315°) \) and \(\sin (315°)\).
- Use the reference angle for \(−\dfrac{π}{6}\) to find \( \cos \left(−\dfrac{π}{6}\right) \) and \( \sin \left(−\dfrac{π}{6}\right)\)
- Answer
-
- \( \cos (315°)= \dfrac{\sqrt{2}}{2}, \quad \sin (315°)=\dfrac{–\sqrt{2}}{2}\)
- \(\cos \left(−\dfrac{π}{6}\right)=\dfrac{\sqrt{3}}{2}, \quad \sin \left(−\dfrac{π}{6}\right)=−\dfrac{1}{2} \)
Because the cosine and sine values for special angles in the first quadrant are known, we can use symmetry and reference angles to fill in cosine and sine values for the rest of the special angles on the unit circle. The complete unit circle appears at the end of this section in Figure \(\PageIndex{19}\). This ENTIRE circle does NOT need to be memorized. Just learning the information that is in Quadrant I as illustrated in Table \(\PageIndex{4}\) or Figure \(\PageIndex{4}\) is all that is needed. Take time to learn the sine and cosine values for all the major angles in the first quadrant! From this information, the trigonometric ratio of any angle can be determined by determining the sign of that ratio based on the quadrant the terminal side lies.
Use a Calculator to Find Sine and Cosine
The special values of sine and cosine in the first quadrant are very useful to know, since knowing them allows you to quickly evaluate the sine and cosine of very common angles without needing to look at a reference or use your calculator. However, scenarios do come up where we need to know the sine and cosine of other angles.
To find the cosine and sine of any other angle, we turn to a computer or calculator. Be aware: most calculators can be set into “degree” or “radian” mode, which tells the calculator the units for the input value. When you evaluate “cos(30)” on your calculator, it will evaluate it as the cosine of 30 degrees if the calculator is in degree mode, or the cosine of 30 radians if the calculator is in radian mode. Most computer software with cosine and sine functions only operate in radian mode.
![]() Howto: Use a calculator to find the sine or cosine of an angle.
Howto: Use a calculator to find the sine or cosine of an angle.
- If the angle is in radians, set the calculator to radian mode; if the angle is in degrees, set the calculator to degree mode.
- Press the COS key or SIN key.
- Enter the value of the angle, press the close-parentheses key ")" and press ENTER.
Example \(\PageIndex{8}\): Use a Calculator to Find Sine and Cosine
- Use a calculator to evaluate \( \cos \left(\dfrac{5π}{3}\right)\).
- Use a calculator to evaluate the cosine of 20°.
Solution
1. Make sure you are in radian mode because the angle is in radians. Then enter the following keystrokes: \(\mathrm{COS( 5 × π ÷ 3 ) \; ENTER}\).
The result obtained is 0.5
2. Make sure you are in degree mode because the angle is in degrees. Then enter the following keystrokes: \(\mathrm{COS( 20 ) \; ENTER}\)
The result is approximately 0.939693.
If the calculator does not have degree mode, the angle must be converted to radians: \(\mathrm{COS( 20 × 180 ÷ π ) \; ENTER} \)
![]() Try It \(\PageIndex{8}\)
Try It \(\PageIndex{8}\)
Evaluate \(\sin \left( \dfrac{π}{3} \right) \).
- Answer
-
approximately 0.866025
Identify the Domain and Range of Sine and Cosine Functions
Now that we can find the sine and cosine of an angle, we need to discuss their domains and ranges.
What are the domains of the sine and cosine functions? The arguments to the sine and cosine function can be any angle, positive or negative. Therefore the input to the sine and cosine functions can be any real number. Thus the domain is \((-\infty, \infty) \).
What are the ranges of the sine and cosine functions? What are the least and greatest possible values for their output? Using the Pythagorean Identity \(\cos ^{2} (\theta )+\sin ^{2} (\theta )=1\), we can see that each term at a minimum can be \(0\), which makes the square of the other term at most \(1\). Thus \(−1 \le \sin \theta \le 1\) and \(−1 \le \cos \theta \le 1\). In other words, the range of both the sine and cosine functions is \([−1,1]\).
Find Coordinates on a Circle
Notice that the definitions for sine and cosine can also be stated in the following form.
![]() How to: Find coordinates of a point given \(r\) and an angle .
How to: Find coordinates of a point given \(r\) and an angle .
Given a circle of radius \(r\) at an angle \(\theta\), then the coordinates of the point (\(x\), \(y\)) on that circle where it intersects the terminal side of the standard position angle \(\theta\) are:
\(x=r\cos (\theta )\)
\(y=r\sin (\theta )\)
Example \(\PageIndex{9a}\): Find coordinates of a point on a circle given \(r\) and an angle.
Find the coordinates of the point on a circle of radius 6 at an angle of \(\dfrac{\pi }{4}\).
Solution
Using our knowledge that \(\sin \left(\dfrac{\pi }{4} \right)=\dfrac{\sqrt{2} }{2}\) and \(\cos \left(\dfrac{\pi }{4} \right)=\dfrac{\sqrt{2} }{2}\), along with our relationships that stated \(x=r\cos (\theta )\) and \(y=r\sin (\theta )\), we can find the coordinates of the point desired:
\[x=6\cos \left(\dfrac{\pi }{4} \right)=6\left(\dfrac{\sqrt{2} }{2} \right)=3\sqrt{2}\nonumber \] \[y=6\sin \left(\dfrac{\pi }{4} \right)=6\left(\dfrac{\sqrt{2} }{2} \right)=3\sqrt{2}\nonumber\]
![]() Try It \(\PageIndex{9a}\)
Try It \(\PageIndex{9a}\)
Find the coordinates of the point on a circle of radius 3 at an angle of \(90{}^\circ\).
- Answer
-
\[\begin{array}{l} {x=3\cos \left(\dfrac{\pi }{2} \right)=3\cdot 0=0} \\ {y=3\sin \left(\dfrac{\pi }{2} \right)=3\cdot 1=3} \end{array}\nonumber\]
Example \(\PageIndex{9b}\): Find coordinates of a point on a circle given \(r\) and an angle .
- Find the coordinates of the point on a circle of radius 12 at an angle of \(\dfrac{7\pi }{6}\).
- Find the coordinates of the point on the unit circle at an angle of \(\dfrac{7π}{6}\).
1. Solution
Note that this angle is in the third quadrant, where both x and y are negative. Keeping this in mind can help you check your signs of the sine and cosine function.
\[x=12\cos \left(\dfrac{7\pi }{6} \right)=12\left(\dfrac{-\sqrt{3} }{2} \right)=-6\sqrt{3}\nonumber \] \[y=12\sin \left(\dfrac{7\pi }{6} \right)=12\left(\dfrac{-1}{2} \right)=-6\nonumber\]
The coordinates of the point are \((-6\sqrt{3} ,-6)\).
2. Solution
We know that the angle \(\dfrac{7π}{6}\) is in the third quadrant. Because this angle is a reduced multiple of \(\dfrac{π}{6}\), its reference angle is simply \(\dfrac{π}{6}\)
Next, we will find the cosine and sine of the reference angle: \(\cos \left( \dfrac{π}{6} \right) =\dfrac{3}{2} \;\; \sin \left(\dfrac{π}{6}\right)=\dfrac{1}{2} \)
We must determine the appropriate signs for \(x\) and \(y\) in the given quadrant. Because our original angle is in the third quadrant, where both \(x\) and \(y\) are negative, both cosine and sine are negative.
\[\begin{align*} \cos \left(\dfrac{7π}{6}\right) &=−\dfrac{\sqrt{3}}{2} \\ \sin \left(\dfrac{7π}{6}\right) & =−\dfrac{1}{2} \end{align*}\]
Now we can calculate the \((x,y)\) coordinates on the unit circle, where \(r=1\), are \(x= \cos θ\) and \(y= \sin θ\).
The coordinates of the point on the unit circle are \(\left(−\dfrac{\sqrt{3}}{2},−\dfrac{1}{2}\right)\).
![]() Try It \(\PageIndex{9b}\)
Try It \(\PageIndex{9b}\)
Find the coordinates of the point on a circle of radius 5 at an angle of \(\dfrac{5\pi }{3}\).
- Answer
-
\[\left(5\cos \left(\dfrac{5\pi }{3} \right),5\sin \left(\dfrac{5\pi }{3} \right)\right)=\left(\dfrac{5}{2} ,\dfrac{-5\sqrt{3} }{2} \right)\nonumber\]
Example \(\PageIndex{10}\)
We now have the tools to return to the sailboat question posed at the beginning of this section.
Solution
A distress signal is sent from a sailboat during a storm, but the transmission is unclear and the rescue 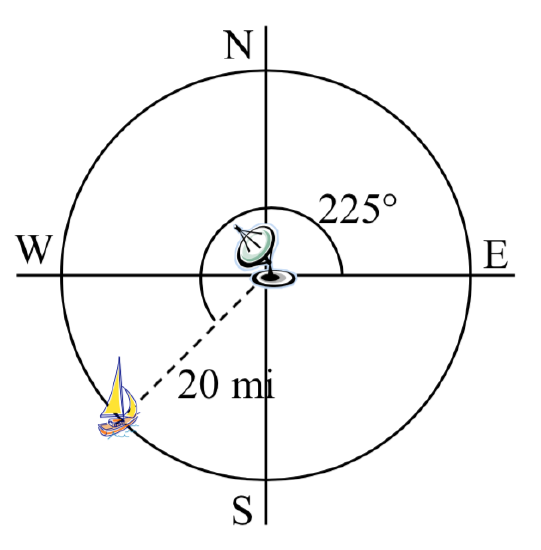 boat sitting at the marina cannot determine the sailboat’s location. Using high powered radar, they determine the distress signal is coming from a point 20 miles away at an angle of 225 degrees from the marina. How many miles east/west and north/south of the rescue boat is the stranded sailboat?
boat sitting at the marina cannot determine the sailboat’s location. Using high powered radar, they determine the distress signal is coming from a point 20 miles away at an angle of 225 degrees from the marina. How many miles east/west and north/south of the rescue boat is the stranded sailboat?
We can now answer the question by finding the coordinates of the point on a circle with a radius of 20 miles at an angle of 225 degrees.
\[x=20\cos \left(225{}^\circ \right)=20\left(\dfrac{-\sqrt{2} }{2} \right)\approx -14.142\text{ miles}\nonumber\]
\[y=20\sin \left(225{}^\circ \right)=20\left(\dfrac{-\sqrt{2} }{2} \right)\approx -14.142\text{ miles}\nonumber\]
The sailboat is located 14.142 miles west and 14.142 miles south of the marina.
Key Equations
| Cosine | \( \cos t=x\) |
| Sine | \( \sin t=y\) |
| Pythagorean Identity | \( \cos ^2 t+ \sin ^2 t=1\) |
Key Concepts
- Finding the function values for the sine and cosine begins with drawing a unit circle, which is centered at the origin and has a radius of 1 unit.
- Using the unit circle, the sine of an angle \(\theta\) equals the \(y\)-value of the endpoint on the unit circle of an arc of length \(\theta\) whereas the cosine of an angle \(\theta\) equals the \(x\)-value of the endpoint.
- The sine and cosine values are most directly determined when the corresponding point on the unit circle falls on an axis.
- When the sine or cosine is known, we can use the Pythagorean Identity to find the other. The Pythagorean Identity is also useful for determining the sines and cosines of special angles.
- Calculators and graphing software are helpful for finding sines and cosines if the proper procedure for entering information is known.
- The domain of the sine and cosine functions is all real numbers.
- The range of both the sine and cosine functions is \([−1,1]\).
- The sine and cosine of an angle have the same absolute value as the sine and cosine of its reference angle.
- The signs of the sine and cosine are determined from the \(x\)- and \(y\)-values in the quadrant of the original angle.
- An angle’s reference angle is the size angle, \(\alpha\), formed by the terminal side of the angle \(\theta\) and the horizontal axis.
- Reference angles can be used to find the sine and cosine of the original angle.
- Reference angles can also be used to find the coordinates of a point on a circle.
Glossary
- cosine function
- the \(x\)-value of the point on a unit circle corresponding to a given angle
- Pythagorean Identity
- a corollary of the Pythagorean Theorem stating that the square of the cosine of a given angle plus the square of the sine of that angle equals 1
- sine function
- the \(y\)-value of the point on a unit circle corresponding to a given angle
- unit circle
- a circle with a center at \((0,0)\) and radius 1.
-
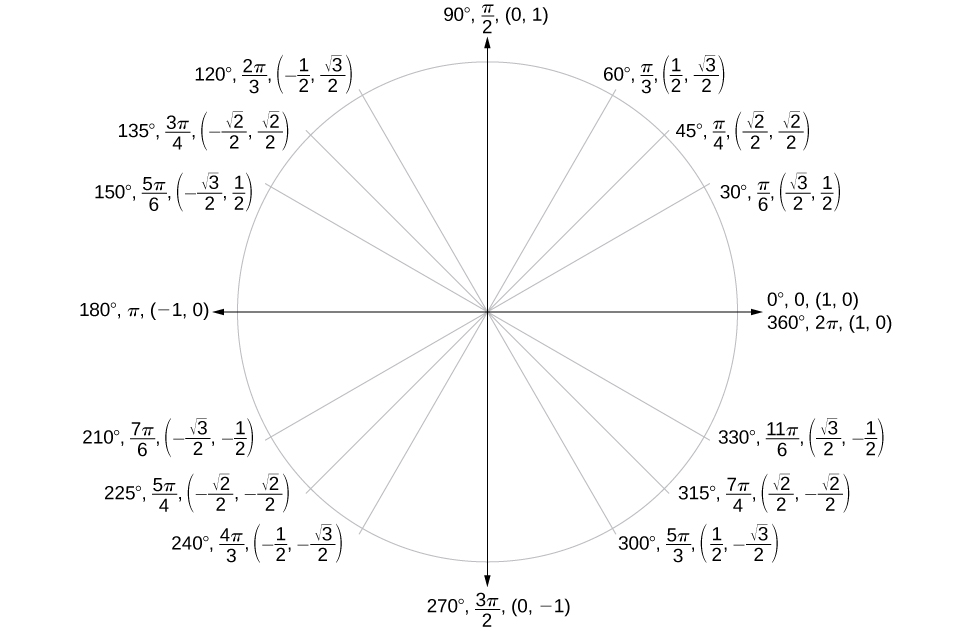
Figure \(\PageIndex{19}\): The Unit Circle. Special angles and their coordinates \((\cos\theta, \sin \theta)\) on the unit circle
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.

