7.1: Non-right Triangles - Law of Sines
- Page ID
- 34939
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives.
- Use the Law of Sines to solve oblique triangles and applied problems
In any triangle, we can draw an altitude, a perpendicular line from one vertex to the opposite side, forming two right triangles. It would be preferable, however, to have methods that we can apply directly to non-right triangles without first having to create right triangles.
Any triangle that is not a right triangle is an oblique triangle. It could be an acute triangle (all three angles of the triangle are less than right angles) or it could be an obtuse triangle (one of the three angles is greater than a right angle). Solving an oblique triangle means finding the measurements of all three angles and all three sides. To do so, we need to start with at least three of these values, including at least one of the sides. We will investigate three possible oblique triangle problem situations:
|
ASA (angle-side-angle)
|
AAS (angle-angle-side)
|
SSA (side-side-angle)
|
Knowing how to approach each of these situations enables oblique triangles to be solved without having to drop a perpendicular to form two right triangles. Instead, the fact that the ratio of the measurement of one of the angles to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side can be used. This statement is derived by considering the triangle in Figure \(\PageIndex{1}\).
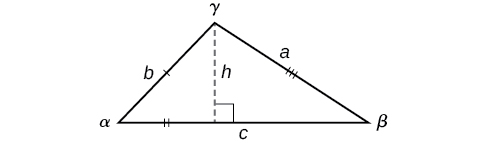
\( \qquad \quad \sin \alpha=\dfrac{h}{b}\) and \(\sin \beta=\dfrac{h}{a}\)
Using right triangle relationships, equations can be found for \(\sin \alpha\) and \(\sin \beta\). Solving both equations for \(h\) gives two different expressions for \(h\), \(h=b \sin \alpha\) and \(h=a \sin \beta\).
\[\begin{align*} b \sin \alpha&= a \sin \beta && \text{Equate expressions for } h \\
\dfrac{ \left(b \sin \alpha\right) }{ab} &= \dfrac{ \left(a \sin \beta\right) }{ab} && \text{Divide both sides by } ab \\
\dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b} && \text{Equivalent side/angle ratios }\end{align*}\]
Similarly, ratios between other angle/side pairs can be obtained. Together, these relationships are called the Law of Sines.
LAW OF SINES
Given a triangle with angles and opposite sides labeled as in the figure to the right, the ratio of the measurement of an angle to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. All proportions will be equal.
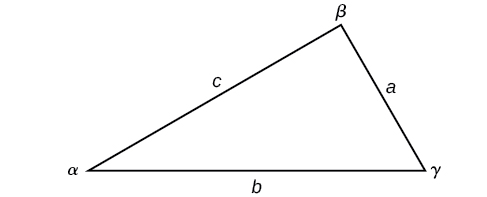The Law of Sines is based on proportions and is presented symbolically two ways.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
\(\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\)
To solve an oblique triangle, use any pair of applicable ratios.
Note the standard way of labeling triangles: angle \(\alpha\) (alpha) is opposite side \(a\); angle \(\beta\) (beta) is opposite side \(b\); and angle \(\gamma\) (gamma) is opposite side \(c\). Also, when calculating angles and sides, be sure to carry the exact values through to the final answer. Generally, final answers are rounded to the nearest tenth, unless otherwise specified.
Use the Law of Sines to Solve AAS and ASA Triangles (Two Angles and One Side Known)
Example \(\PageIndex{1}\): Solve an AAS Triangle
Solve the triangle illustrated below to the nearest tenth.
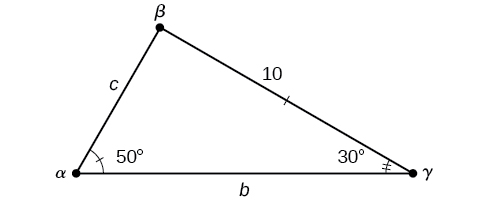
Solution
The three angles must add up to 180 degrees. From this, we can determine that
\( \beta = 180^{\circ} - 50^{\circ} - 30^{\circ} = 100^{\circ} \)
To find an unknown side, we need to know the corresponding angle and a known ratio. We know angle \(\alpha=50°\)and its corresponding side \(a=10\). The following proportion from the Law of Sines can be used to find the length of \(c\).
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(30^{\circ})}{c}\\
c \cdot \dfrac{\sin(50^{\circ})}{10}&= \sin(30^{\circ}) && \text{Multiply both sides by } c\\
c&= \sin(30^{\circ})\dfrac{10}{\sin(50^{\circ})} \approx 6.5 && \text{Multiply by the reciprocal to isolate } c
\end{align*}\]
Similarly, to solve for \(b\), we set up another proportion.
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(100^{\circ})}{b}\\
b \sin(50^{\circ})&= 10 \sin(100^{\circ}) &&\text{Multiply both sides by } b\\
b&= \dfrac{10 \sin(100^{\circ})}{\sin(50^{\circ})} \approx 12.9 && \text{Multiply by the reciprocal to isolate }b \end{align*}\]
Therefore, the complete set of angles and sides is: \( \qquad \begin{matrix} \alpha=50^{\circ} & a=10\\ \beta=100^{\circ} & b\approx 12.9\\ \gamma=30^{\circ} & c\approx 6.5 \end{matrix}\)
Try It \(\PageIndex{1}\): Solve an ASA triangle
Solve the triangle shown below to the nearest tenth.
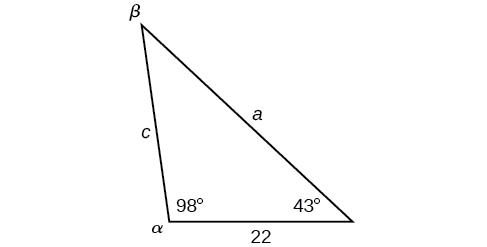
- Answer
-
\(\begin{matrix} \alpha=98^{\circ} & a \approx 34.6\\ \beta=39^{\circ} & b=22\\ \gamma=43^{\circ} & c \approx 23.8 \end{matrix}\)
Use the Law of Sines to Solve SSA Triangles (Two Sides and One Angle Known)
We can use the Law of Sines to solve any oblique triangle, but some solutions may not be straightforward. In some cases, more than one triangle may satisfy the given criteria, which we describe as an ambiguous case. Triangles classified as SSA, those in which we know the lengths of two sides and the measurement of the angle opposite one of the given sides, may result in one or two solutions, or even no solution.
POSSIBLE OUTCOMES FOR SSA TRIANGLES
Oblique triangles in the category SSA may have four different outcomes. Figure \(\PageIndex{2}\) illustrates the solutions with the known sides \(a\) and \(b\) and known angle \(\alpha\). When angle \( \alpha \) is obtuse, there are only two outcomes: no triangle when \( a \le b \) and one triangle when \( a > b\).
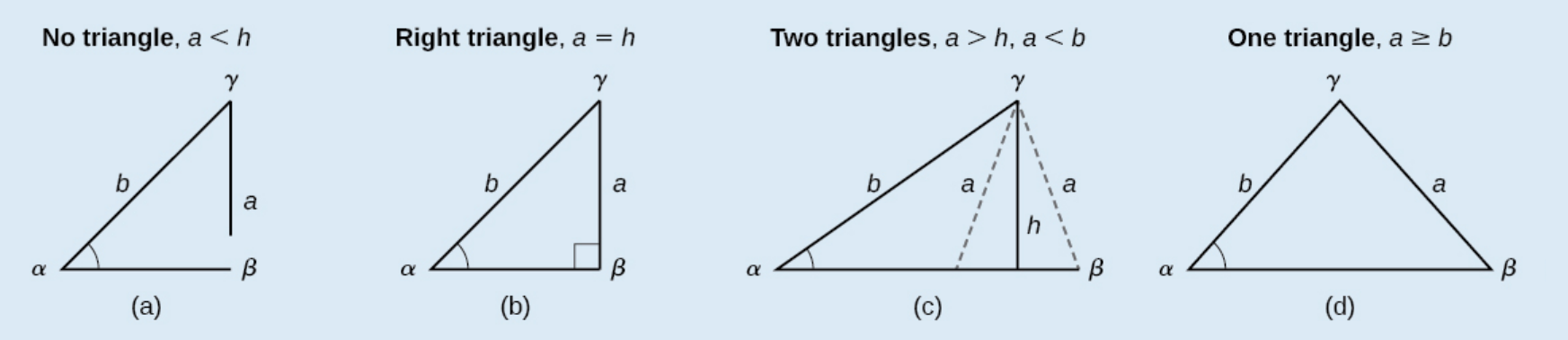
Figure \(\PageIndex{2}\) Sides \(a\) and \(b\) and angle \(\alpha\) are given. The height of the triangle is \(h\).
The angle determined, \(\beta\), (a) Does not exist, (b) is equal to \(90^\circ\), (c) is greater than \(\alpha\), or (d) is less than \(\alpha\).
Example \(\PageIndex{2}\): Solve an Oblique SSA Triangle
Solve the triangle in the diagram below for the missing side and find the missing angle measures to the nearest tenth.
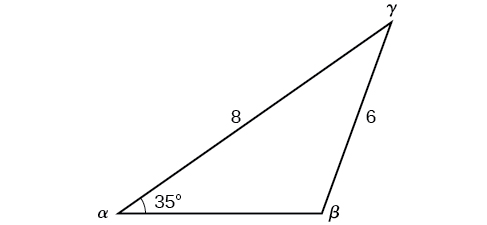
Solution
Use the Law of Sines to find angle \(\beta\) and angle \(\gamma\), and then side \(c\). Solving for \(\beta\), we have the proportion
\[\begin{align*} \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b}\\ \dfrac{\sin(35^{\circ})}{6}&= \dfrac{\sin \beta}{8}\\ \dfrac{8 \sin(35^{\circ})}{6}&= \sin \beta\\ 0.7648&\approx \sin \beta\\ {\sin}^{-1}(0.7648)&\approx 49.9^{\circ}\\ \beta&\approx 49.9^{\circ} \end{align*}\]
However, in the diagram, angle \(\beta\) appears to be an obtuse angle and may be greater than \(90°\). How did we get an acute angle, and how do we find the measurement of \(\beta\)? Remember that the sine function is positive in both the first and second quadrants and thus finding an angle using the \( \sin^{-1} \) function will only produce an angle between \( 0°\) and \( 90°\)!! Dropping a perpendicular from \(\gamma\) and viewing the triangle from a right angle perspective, we have Figure \(\PageIndex{2a}\). It appears that there may be a second triangle that will fit the given criteria.
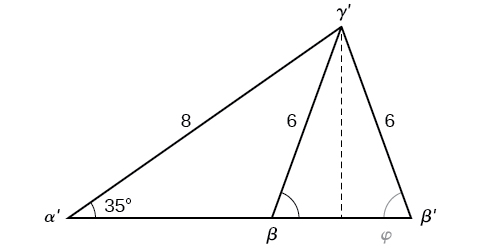
Our calculations have found the angle measure \( \beta' \approx 49.9°\) in the acute triangle. The measure of this angle \(\beta\) in the oblique triangle, is supplementary to \(\beta'\), which means that \(\beta=180°− \beta'\) so \(\beta=180°−49.9°=130.1°\).
Solving for \(\gamma\) in the oblique triangle, we have
\( \gamma= 180^{\circ}-35^{\circ}-130.1^{\circ} \approx 14.9^{\circ} \)
Solving for \(\gamma'\) in the acute triangle, we have
\( \gamma^{'} = 180^{\circ}-35^{\circ}-49.5^{\circ} \approx 95.1^{\circ} \)
Now we need to find \(c\) and \(c′\).
\( \dfrac{c}{\sin(14.9^{\circ})}= \dfrac{6}{\sin(35^{\circ})} \quad \rightarrow \quad c= \dfrac{6 \sin(14.9^{\circ})}{\sin(35^{\circ})} \approx 2.7 \)
and
\( \dfrac{c'}{\sin(95.1^{\circ})} = \dfrac{6}{\sin(35^{\circ})} \quad \rightarrow \quad c'= \dfrac{6 \sin(95.1^{\circ})}{\sin(35^{\circ})} \approx 10.4 \)
To summarize, there are two triangles with an angle of \(35°\), an adjacent side of 8, and an opposite side of 6, as shown in Figure \(\PageIndex{2b}\).
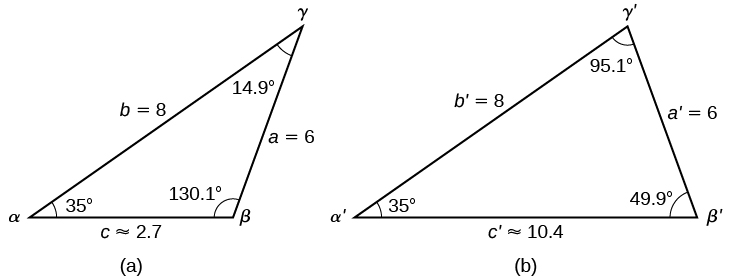
Figure \(\PageIndex{2b}\)
However, we were looking for the values for the triangle with an obtuse angle \(\beta\). We can see them in the first triangle (a) in Figure \(\PageIndex{2b}\).
Try It \(\PageIndex{2}\)
Given \(\alpha=80°\), \(a=120\), and \(b=121\), find the missing side and angles. If there is more than one possible solution, show both.
- Answer
-
\( \begin{array}{l|l}
\bf\text{Solution 1} & \bf\text{Solution 2}\\
\begin{matrix} \alpha=80^{\circ} & a=120\\ \beta\approx 83.2^{\circ} & b=121\\ \gamma\approx 16.8^{\circ} & c\approx 35.2 \end{matrix} &
\begin{matrix} \alpha '=80^{\circ} & a'=120\\ \beta '\approx 96.8^{\circ} & b'=121\\ \gamma '\approx 3.2^{\circ} & c'\approx 6.8 \end{matrix} \\
\end{array} \)
Example \(\PageIndex{3}\): Solve an Acute SSA Triangle
In the triangle shown below, solve for the unknown side and angles. Round your answers to the nearest tenth.
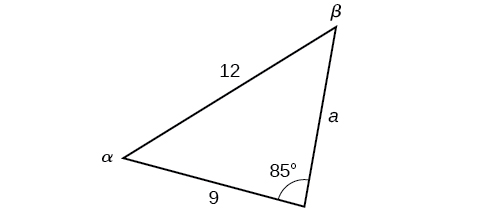
Solution
In choosing the pair of ratios from the Law of Sines to use, look at the information given. In this case, we know the angle, \(\gamma=85°\), and its corresponding side \(c=12\), and we know side \(b=9\). We will use this proportion to solve for \(\beta\).
\[\begin{align*} \dfrac{\sin(85^{\circ})}{12}&= \dfrac{\sin \beta}{9}\qquad \text{Isolate the unknown.}\\ \dfrac{9 \sin(85^{\circ})}{12}&= \sin \beta \end{align*}\]
To find \(\beta\), apply the inverse sine function. The inverse sine will produce a single result, but keep in mind that there may be two values for \(\beta\). It is important to verify the result, as there may be two viable solutions, only one solution (the usual case), or no solutions.
\( \beta = {\sin}^{-1}\left(\dfrac{9 \sin(85^{\circ})}{12}\right) \approx {\sin}^{-1} (0.7471) \approx 48.3^{\circ} \)
Because one solution has been found, and this is an SSA triangle, there may be a second possible solution. The other possivle angle is found by subtracting \(\beta\) from \(180°\), so \(\beta=180°−48.3°≈131.7°\). To check if this is also a solution, subtract both angles, the given angle \(\gamma=85°\) and the calculated angle \(\beta=131.7°\), from \(180°\). This gives
\( \alpha = 180^{\circ}-85^{\circ}-131.7^{\circ} \approx -36.7^{\circ} \)
which is impossible, and so there is only one possible solution, \(\beta≈48.3°\).
To find the remaining missing values, we calculate \(\alpha=180°−85°−48.3°≈46.7°\). Now, only side \(a\) is needed. Use the Law of Sines to solve for \(a\) by one of the proportions.
\[\begin{align*} \dfrac{\sin(85°)}{12}&= \dfrac{\sin(46.7^{\circ})}{a}\\ a \cdot \dfrac{\sin(85^{\circ})}{12}&= \sin(46.7^{\circ})\\ a&=\dfrac{12\sin(46.7^{\circ})}{\sin(85^{\circ})} \approx 8.8 \end{align*}\]
The complete set of solutions for the given triangle is: \( \qquad\) \(\begin{matrix} \alpha\approx 46.7^{\circ} & a\approx 8.8\\ \beta\approx 48.3^{\circ} & b=9\\ \gamma=85^{\circ} & c=12 \end{matrix}\)
Try It \(\PageIndex{3}\)
Given \(\alpha=80°\), \(a=100\), \(b=10\), find the missing side and angles. If there is more than one possible solution, show both. Round your answers to the nearest tenth.
- Answer
-
\(\beta≈5.7°\), \(\gamma≈94.3°\), \(c≈101.3\)
Example \(\PageIndex{4}\): Solve a Triangle That Does Not Meet the Given Criteria
Find all possible triangles if one side has length \(4\) opposite an angle of \(50°\), and a second side has length \(10\).
Solution
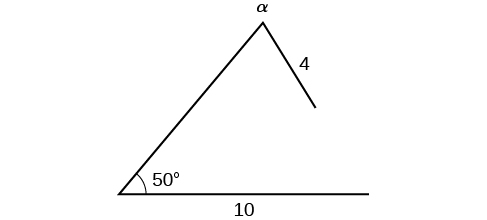
Using the given information, we can solve for the angle opposite the side of length \(10\). See Figure \(\PageIndex{4}\).
\[\begin{align*} \dfrac{\sin \alpha}{10}&= \dfrac{\sin(50^{\circ})}{4}\\ \sin \alpha&= \dfrac{10 \sin(50^{\circ})}{4}\\ \sin \alpha&\approx 1.915 \end{align*}\]
We can stop here without finding the value of \(\alpha\). Because the range of the sine function is \([ −1,1 ]\), it is impossible for the sine value to be \(1.915\). In fact, inputting \({\sin}^{−1}(1.915)\) in a graphing calculator generates an ERROR DOMAIN. Therefore, no triangles can be drawn with the provided dimensions.
Try It \(\PageIndex{4}\)
Determine the number of triangles possible given \(a=31\), \(b=26\), \(\beta=48°\).
- Answer
-
two
Applied Problems Using the Law of Sines
The more we study trigonometric applications, the more we discover that the applications are countless. Some are flat, diagram-type situations, but many applications in calculus, engineering, and physics involve three dimensions and motion.
Example \(\PageIndex{6}\): Find Altitude
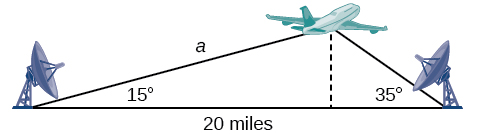Suppose two radar stations located \(20\) miles apart each detect an aircraft between them. The angle of elevation measured by the first station is \(35\) degrees, whereas the angle of elevation measured by the second station is \(15\) degrees, shown here. Find the altitude of the aircraft. Round the altitude to the nearest tenth of a mile.
Solution
To find the elevation of the aircraft, we first find the distance from one station to the aircraft, such as the side \(a\), and then use right triangle relationships to find the height of the aircraft, \(h\).
Because the angles in the triangle add up to \(180\) degrees, the unknown angle must be \(180°−15°−35°=130°\). This angle is opposite the side of length \(20\), allowing us to set up a Law of Sines relationship.
\[\begin{align*} \dfrac{\sin(130^{\circ})}{20}&= \dfrac{\sin(35^{\circ})}{a}\\ a \sin(130^{\circ})&= 20 \sin(35^{\circ})\\ a&= \dfrac{20 \sin(35^{\circ})}{\sin(130^{\circ})} \approx 14.98 \end{align*}\]
The distance from one station to the aircraft is about \(14.98\) miles.
Now that we know \(a\), we can use right triangle relationships to solve for \(h\).
\[\begin{align*} \sin(15^{\circ})&= \dfrac{opposite}{hypotenuse}\\ \sin(15^{\circ})&= \dfrac{h}{a}\\ \sin(15^{\circ})&= \dfrac{h}{14.98}\\ h&= 14.98 \sin(15^{\circ}) \approx 3.88 \end{align*}\]
The aircraft is at an altitude of approximately \(3.9\) miles.
Try It \(\PageIndex{6}\)
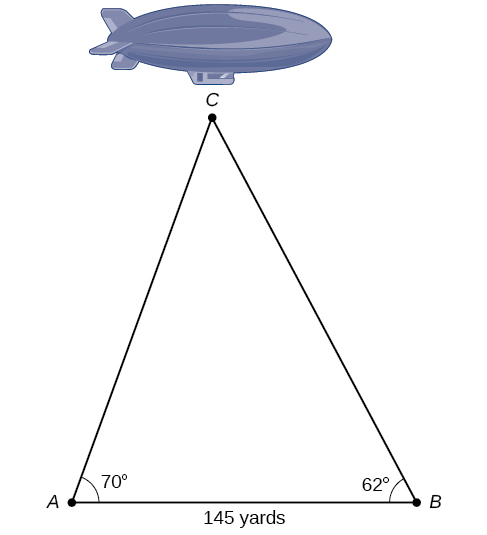The accompanying diagram represents the height of a blimp flying over a football stadium. Find the height of the blimp if the angle of elevation at the southern end zone, point A, is \(70°\), the angle of elevation from the northern end zone, point B, is \(62°\), and the distance between the viewing points of the two end zones is \(145\) yards.
- Answer
-
\(161.9\) yd.
Key Equations
|
Law of Sines |
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\) |
\(\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\) |
|
Area for oblique triangles |
\(Area=\dfrac{1}{2}bc \sin \alpha\) |
\(=\dfrac{1}{2} ac \sin \beta\) \(=\dfrac{1}{2} ab \sin \gamma\) |
Key Concepts
- The Law of Sines can be used to solve oblique triangles, which are non-right triangles.
- According to the Law of Sines, the ratio of the measurement of one of the angles to the length of its opposite side equals the other two ratios of angle measure to opposite side.
- There are three possible cases: ASA, AAS, SSA. Depending on the information given, we can choose the appropriate equation to find the requested solution.
- The ambiguous case arises when an oblique triangle can have different outcomes.
- There are three possible cases that arise from SSA arrangement—a single solution, two possible solutions, and no solution.
- The Law of Sines can be used to solve triangles with given criteria.
- The general area formula for triangles translates to oblique triangles by first finding the appropriate height value.
- There are many trigonometric applications. They can often be solved by first drawing a diagram of the given information and then using the appropriate equation.
Contributors
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.