7.5: The Dot Product

Learning Objectives 

• Calculate the dot product of two given vectors.
• Determine whether two given vectors are perpendicular.
• Explain what is meant by the vector projection of one vector onto another vector, and describe how to compute it.
• Calculate the work done by a given force.

If we apply a force to an object so that the object moves, we say that work is done by the force. Previously, we looked at a constant force and we assumed the force was applied in the direction of motion of the object. Under those conditions, work can be expressed as the product of the force acting on an object and the distance the object moves. In this chapter, however, we have seen that both force and the motion of an object can be represented by vectors.

In this section, we develop an operation called the dot product, which allows us to calculate work in the case when the force vector and the motion vector have different directions. The dot product essentially tells us how much of the force vector is applied in the direction of the motion vector. The dot product can also help us measure the angle formed by a pair of vectors and the position of a vector relative to the coordinate axes. It even provides a simple test to determine whether two vectors meet at a right angle.

The Dot Product and Its Properties

We have already learned how to add and subtract vectors. In this chapter, we investigate two types of vector multiplication. The first type of vector multiplication is called the dot product, based on the notation we use for it, and it is defined as follows:

Definition: dot product

The dot product  (also called the scalar product) of two vectors \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) and \(\vecs{ v}=⟨v_1,v_2,v_3⟩\) is given by the sum of the products of the components

\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3.\)

When vectors are written in standard unit vector form,  \(\vecs{ u}=u_1\hat{\textbf i} + u_2\hat{\textbf j} + u_3\hat{\textbf k} \) and \(\vecs{ v}=v_1\hat{\textbf i} + v_2\hat{\textbf j} + v_3\hat{\textbf k}\) the dot product is the same sum of products. Notice the standard unit vectors themselves are not included in the dot product.

\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3.\)

Note that if \(u\) and \(v\) are two-dimensional vectors, we calculate the dot product in a similar fashion. Thus, if \(\vecs{ u}=⟨u_1,u_2⟩\) and \(\vecs{ v}=⟨v_1,v_2⟩,\) then

\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2.\)

When two vectors are combined under addition or subtraction, the result is a vector. When two vectors are combined using the dot product, the result is a scalar. For this reason, the dot product is often called the scalar product. It may also be called the inner product.

Example \(\PageIndex{1}\): Calculate Dot Products

1. Find the dot product of \(\vecs{ u}=⟨3,5,2⟩\) and \(\vecs{ v}=⟨−1,3,0⟩\).
2. Find the scalar product of \(\vecs{ p}=10\hat{\textbf i}−4 \hat{\textbf j}+7 \hat{\textbf k}\) and \(\vecs{ q}=−2\hat{\textbf i}+\hat{\textbf j}+6\hat{\textbf k}.\)

Solution:

a. Substitute the vector components into the formula for the dot product:

\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &=3(−1)+5(3)+2(0) \\[4pt] &=−3+15+0 =12. \end{align*}\]

b. The calculation is the same if the vectors are written using standard unit vectors. We still have three components for each vector to substitute into the formula for the dot product:

\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &=10(−2)+(−4)(1)+(7)(6) \\[4pt] &=−20−4+42  =18.\end{align*}\]

Try It \(\PageIndex{1}\)

1. Find \(\vecs{ u}⋅\vecs{ v}\), where \(\vecs{ u}=⟨2,9,−1⟩\) and \(\vecs{ v}=⟨−3,1,−4⟩.\)
2. Find \(\vecs{ u}⋅\vecs{ v}\), where \(\vecs{ u}= −8\hat{\mathbf i}+3\hat{\mathbf j} \) and \(\vecs{ v}= 2\hat{\mathbf i}+9\hat{\mathbf j} .\)

Hint

Multiply corresponding components and then add their products.

Answer

a. \(7 \qquad\) b. \( 11\)

Like vector addition and subtraction, the dot product has several algebraic properties. 

Magnitude of a vector and the Dot Product

The dot product of a vector  \(\vecs{ v}\) with itself is the square of its magnitude: 

\[\vecs{ v}⋅\vecs{ v}=\|\vecs{ v}\|^2\]

Example \(\PageIndex{2}\): Dot Product Expressions

Let \(\vecs{ a}=⟨1,2,−3⟩\), \(\vecs{ b}=⟨0,2,4⟩\), and \( \vecs{ c} =⟨5,−1,3⟩\).

Find each of the following products.

1. \(( \vecs{ a} ⋅ \vecs{ b}) \vecs{ c} \)
2. \(\vecs{ a}⋅(2\vecs{ c})\)
3. \(\|\vecs{ b}\|^2\)

Solution

a. Note that this expression asks for the scalar multiple of \(\vecs{ c}\) by \(\vecs{ a}⋅\vecs{ b}\):

\[ \begin{align*} (\vecs{ a}⋅\vecs{ b})\vecs{ c} &=(⟨1,2,−3⟩⋅⟨0,2,4⟩)⟨5,−1,3⟩ \\[4pt] &=(1(0)+2(2)+(−3)(4))⟨5,−1,3⟩ \\[4pt] &=(−8)⟨5,−1,3⟩ = ⟨−40,8,−24⟩.\end{align*}\]

b. This expression is a dot product of vector \(\vecs{ a}\) and scalar multiple 2\(\vecs{ c}\):

\[ \begin{align*} \vecs{ a}⋅(2\vecs{ c}) &=⟨1,2,−3⟩⋅2(⟨5,−1,3⟩) \\[4pt] &=⟨1,2,−3⟩⋅⟨10,−2,6⟩ \\[4pt] &=(1)(10)+2(−2)+(−3)(6)) \\[4pt] & =10 - 4 - 18 =−12.\end{align*}\]

c. Simplifying this expression is a straightforward application of the dot product:

\[ \begin{align*} \|\vecs{ b}\|^2 &=\vecs{ b}⋅\vecs{ b} \\[4pt] &=⟨0,2,4⟩⋅⟨0,2,4⟩\\[4pt] &=0^2+2^2+4^2 \\[4pt] &=0+4+16 =20.\end{align*}\]

Try It \(\PageIndex{2}\)

Find the following products for \(\vecs{ p}=7\hat{\textbf i} + 0\hat{\textbf j} + 2\hat{\textbf k} \), \(\vecs{ q}=−2\hat{\textbf i} + 2\hat{\textbf j} −2\hat{\textbf k} \), and \(\vecs{ r}=0\hat{\textbf i} + 2\hat{\textbf j} −3\hat{\textbf k} \).

1. \((\vecs{ r}⋅\vecs{ p})\vecs{ q}\)
2. \(\|\vecs{ p}\|^2\)

Hint

\(\vecs{ r}⋅\vecs{ p}\) is a scalar.

Answer

\(a. \quad (\vecs{ r}⋅\vecs{ p})\vecs{ q}=12\hat{\textbf i} −12\hat{\textbf j} + 12\hat{\textbf k} ; \quad b. \quad \|\vecs{ p}\|^2=53\)

Find the Angle between Two Vectors

When two nonzero vectors are placed in standard position, whether in two dimensions or three dimensions, they form an angle between them. The dot product provides a way to find the measure of this angle. 

 How to: Evaluate the dot product given the magnitude of 2 vectors and the angle between them

Given two non-zero vectors \(\vecs{ u}\) and \(\vecs{ v}\) and the angle between them, \(θ,\) such that \(0≤θ≤π\). 

The dot product of the two vectors is the product of the magnitude of each vector and the cosine of the angle between them:

\(\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{evaldot}\)

Proof

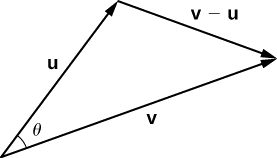Place vectors \(\vecs{ u}\) and \(\vecs{ v}\) in standard position and consider the vector \(\vecs{ v}−\vecs{ u}\) (see the figure on the right). These three vectors form a triangle with side lengths \(‖\vecs{ u}‖,‖\vecs{ v}‖\), and \(‖\vecs{ v}−\vecs{ u}‖\). 

Recall from trigonometry that the law of cosines describes the relationship among the side lengths of the triangle and the angle \(θ\). Applying the law of cosines here gives

\(‖\vecs{ v}−\vecs{ u}‖^2=‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{eq20}\)

The dot product provides a way to rewrite the left side of Equation \ref{eq20}:

\[ \begin{align*} ‖\vecs{ v}−\vecs{ u}‖^2 &=(\vecs{ v}−\vecs{ u})⋅(\vecs{ v}−\vecs{ u}) \\[4pt] &=(\vecs{ v}−\vecs{ u})⋅\vecs{ v}−(\vecs{ v}−\vecs{ u})⋅\vecs{ u} \\[4pt] &=\vecs{ v}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}−\vecs{ v}⋅\vecs{ u}+\vecs{ u}⋅\vecs{ u} \\[4pt] &=\vecs{ v}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ u} \\[4pt] &=‖\vecs{ v}‖^2−2\vecs{ u}⋅\vecs{ v}+‖\vecs{ u}‖^2.\end{align*}\]

Substituting into the law of cosines yields

\[ \begin{align*} ‖\vecs{ v}−\vecs{ u}‖^2 &=‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] ‖\vecs{ v}‖^2−2\vecs{ u}⋅\vecs{ v}+‖\vecs{ u}‖^2 &= ‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \qquad \text{□} \end{align*}\]

(Another proof uses the formula for the cosine of the sum of two angles instead of the Law of Cosines).

We can use the form of the dot product in Equation \ref{evaldot} to find the measure of the angle between two nonzero vectors by rearranging Equation \ref{evaldot} to solve for the cosine of the angle. Using this equation, we can find the cosine of the angle between two nonzero vectors. Since we are considering the smallest angle between the vectors, we assume \(0°≤θ≤180°\) (or \(0≤θ≤π\) if we are working in radians). The inverse cosine is unique over this range, so we are then able to determine the measure of the angle \(θ\).

 How to: Find the angle between two vectors

Given two vectors \( \vecs{ u}\) and \(\vecs{ v}, \) then the smallest angle \( θ \) between them can be found using the equation:

\(\cos θ=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}. \label{dot2}\)

Example \(\PageIndex{3}\): Find the Angle between Two Vectors

Find the measure of the angle between each pair of vectors.

1. \(\mathbf{\hat i} + \mathbf{\hat j} + \mathbf{\hat k}\) and \(2\mathbf{\hat i} – \mathbf{\hat j} – 3\mathbf{\hat k}\)
2. \(⟨2,5,6⟩\) and \(⟨−2,−4,4⟩\)

Solution

a. To find the cosine of the angle formed by the two vectors, substitute the components of the vectors into Equation \ref{dot2}:

\[ \begin{align*} \cos θ &=\dfrac{(\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k})⋅(2\mathbf{\hat i}−\mathbf{\hat j}−3\mathbf{\hat k})}{∥\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k}∥⋅∥2\mathbf{\hat i}−\mathbf{\hat j}−3\mathbf{\hat k}∥} \\[4pt] &=\dfrac{1(2)+(1)(−1)+(1)(−3)}{\sqrt{1^2+1^2+1^2}\sqrt{2^2+(−1)^2+(−3)^2}}  =\dfrac{−2}{\sqrt{3}\sqrt{14}} =\dfrac{−2}{\sqrt{42}}. \end{align*}\]

Therefore, \(θ=\arccos\dfrac{−2}{\sqrt{42}}\)  \( \approx 107.98°\) or \( \approx 1.88\) rad.

b. Start by finding the value of the cosine of the angle between the vectors:

\[ \begin{align*} \cos θ &=\dfrac{⟨2,5,6⟩⋅⟨−2,−4,4⟩}{∥⟨2,5,6⟩∥⋅∥⟨−2,−4,4⟩∥} \\[4pt] &=\dfrac{2(−2)+(5)(−4)+(6)(4)}{\sqrt{2^2+5^2+6^2}\sqrt{(−2)^2+(−4)^2+4^2}}  =\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\]

Now, \(\cos θ=0\) and \(0≤θ≤π\), so \(θ=90°\) or \(π/2\) radians.

Try It \(\PageIndex{3a}\)

Find the measure of the angle, in radians, formed by vectors \(\vecs{ a}=⟨1,2,0⟩\) and \(\vecs{ b}=⟨2,4,1⟩\). Round to the nearest hundredth.

Hint

Use the Equation \ref{dot2}.

Answer

\(θ≈12.61°\) or \(θ≈0.22\) rad

 Try It \(\PageIndex{3b}\)

Let \(\vecs{ v}=⟨3,−5,1⟩.\) Find the measure of the angles formed by each pair of vectors.

1. \(\vecs{ v}\) and \(\mathbf{\hat i}\)
2. \(\vecs{ v}\) and \(\mathbf{\hat j}\)
3. \(\vecs{ v}\) and \(\mathbf{\hat k}\)

Hint

\(\mathbf{\hat i}=⟨1,0,0⟩, \mathbf{\hat j}=⟨0,1,0⟩,\) and \(\mathbf{\hat k}=⟨0,0,1⟩\)

Answer

\(a. α≈1.04\) rad; b. \(β≈2.58\) rad; c. \(γ≈1.40\) rad

Figure \(\PageIndex{3}\) Possible angles between vectors.

Possible angles between two vectors is illustrated in Figure \(\PageIndex{3}\). The angle between two vectors can be (a) acute \((0<\cos θ<1),\) (b) obtuse \((−1<\cos θ<0)\), or (c) straight \((\cos θ=−1)\). If \(\cos θ=1\), then (d) both vectors have the same direction. If \(\cos θ=0\), then the vectors, when placed in standard position, form (e) a right angle. We can formalize this result into a theorem regarding orthogonal (perpendicular) vectors.

Orthogonal Vectors

The nonzero vectors \(\vecs{u}\) and \(\vecs{v}\) are orthogonal vectors if and only if \(\vecs{u}⋅\vecs{v}=0.\)

The terms orthogonal, perpendicular, and normal each indicate that mathematical objects are intersecting at right angles. The use of each term is determined mainly by its context. We say that vectors are orthogonal and lines are perpendicular. The term normal is used most often when measuring the angle made with a plane or other surface.

Example \(\PageIndex{4}\): Identifying Orthogonal Vectors

Determine whether \(\vecs{p}=⟨1,0,5⟩\) and \(\vecs{q}=⟨10,3,−2⟩\) are orthogonal vectors.

Solution

Using the definition, we need only check the dot product of the vectors:

\[ \vecs{ p}⋅\vecs{ q}=1(10)+(0)(3)+(5)(−2)=10+0−10=0. \nonumber\]

Because \(\vecs{p}⋅\vecs{q}=0,\) the vectors are orthogonal (Figure \(\PageIndex{4}\)).

Figure \(\PageIndex{4}\): Vectors \(\vecs{ p}\) and \(\vecs{ q}\) form a right angle when their initial points are aligned.

 Try It \(\PageIndex{4}\)

For which value of \(x\) is \(\vecs{ p}=⟨2,8,−1⟩\) orthogonal to \(\vecs{ q}=⟨x,−1,2⟩\)?

Hint

Vectors \(\vecs{ p}\) and \(\vecs{ q}\) are orthogonal if and only if \(\vecs{ p}⋅\vecs{ q}=0\).

Answer

\(x=5\)

Projections

As we have seen, addition combines two vectors to create a resultant vector. But what if we are given a vector and we need to find its component parts? We use vector projections to perform the opposite process; they can break down a vector into its components. The magnitude of a vector projection is a scalar projection. For example, if a child is pulling the handle of a wagon at a 55° angle, we can use projections to determine how much of the force on the handle is actually moving the wagon forward (\(\PageIndex{6}\)). We return to this example and learn how to solve it after we see how to calculate projections.

Figure \(\PageIndex{6}\): When a child pulls a wagon, only the horizontal component of the force propels the wagon forward.

Definition: Vector Projection

Figure \(\PageIndex{7}\): Vector Projection.

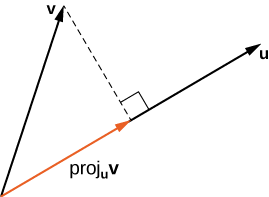
The vector projection of \(\vecs{ v}\) onto \(\vecs{ u}\) is the portion of\( \vecs{v}\) that is in the direction of \(\vecs{ u}\). This is the vector labeled \(\text{proj}_\vecs{ u}\vecs{ v}\) in Figure \(\PageIndex{7}\). It has the same initial point as \(\vecs{ u}\) and \(\vecs{ v}\) and the same direction as \(\vecs{ u}\), and represents the component of \(\vecs{ v}\) that acts in the direction of \(\vecs{ u}\).

If \(θ\) represents the angle between \(\vecs{ u}\) and \(\vecs{ v}\), then, by properties of triangles, we know the length of \(\text{proj}_\vecs{ u}\vecs{ v}\) is \(\|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs{ v}‖\cos θ,\) which can also be expressed in terms of the dot product.

The magnitude of the projection of \(\vecs{ v}\) onto \(\vecs{ u}\):

\[ \|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs v‖\cos θ=‖\vecs{ v}‖\left(\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}\right)=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖.}\]

We now multiply by a unit vector in the direction of \(\vecs{ u}\) to get \(\text{proj}_\vecs{ u}\vecs{ v}\), the vector that is the projection of \(\vecs{ v}\) onto \(\vecs{ u}\):

\[\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\left(\dfrac{1}{‖\vecs{ u}‖}\vecs{ u}\right)=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}.\]

Example \(\PageIndex{5}\): Finding Projections

Find the projection of \(\vecs{ v}\) onto \(\vecs{ u}\).

1. \(\vecs{v}=⟨3,5,1⟩\) and \(\vecs{u}=⟨−1,4,3⟩\)
2. \(\vecs{v}=3\mathbf{\hat i}−2\mathbf{\hat j}\) and \(\vecs{u}=\mathbf{\hat i}+6\mathbf{\hat j}\)

Solution

a. Substitute the components of \(\vecs{ v}\) and \(\vecs{ u}\) into the formula for the projection:  

\(\begin{align*} \text{proj}_\vecs{ u}\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt]
&=\dfrac{⟨−1,4,3⟩⋅⟨3,5,1⟩}{∥⟨−1,4,3⟩∥^2} \big \langle −1,4,3 \big \rangle \\[4pt]
&=\dfrac{−3+20+3}{(−1)^2+4^2+3^2} \big \langle −1,4,3 \big \rangle \\[4pt]
&=\dfrac{20}{26} \big \langle −1,4,3 \big \rangle \\[4pt]
&= \left \langle−\dfrac{10}{13},\dfrac{40}{13},\dfrac{30}{13}\right \rangle. \end{align*}\)

b. To find the two-dimensional projection, simply adapt the formula to the two-dimensional case:

\(\begin{align*} \text{proj}_\vecs{ u}\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt]
&=\dfrac{(\mathbf{\hat i}+6\mathbf{\hat j})⋅(3i−2j)}{∥\mathbf{\hat i}+6\mathbf{\hat j}∥^2}(\mathbf{\hat i}+6\mathbf{\hat j})j) \\[4pt]
&= \dfrac{1(3)+6(−2)}{1^2+6^2}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt]
&= −\dfrac{9}{37}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt]
&= −\dfrac{9}{37}\mathbf{\hat i}−\dfrac{54}{37}\mathbf{\hat j}.\end{align*}\)

Sometimes it is useful to decompose vectors—that is, to break a vector apart into a sum. This process is called the resolution of a vector into components. Projections allow us to identify two orthogonal vectors having a desired sum. For example, let \(\vecs{ v}=⟨6,−4⟩\) and let \(\vecs{ u}=⟨3,1⟩.\) We want to decompose the vector \(\vecs{ v}\) into orthogonal components such that one of the component vectors has the same direction as \(\vecs{ u}\).

We first find the component that has the same direction as \(\vecs{ u}\) by projecting \(\vecs{ v}\) onto \(\vecs{ u}\). Let \(\vecs{ p}=\text{proj}_\vecs{ u}\vecs{ v}\). Then, we have

\[\begin{align*}\vecs{ p} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} = \dfrac{18−4}{9+1}\vecs{ u} = \dfrac{7}{5}\vecs{ u} \\[4pt]
&=\dfrac{7}{5} \big \langle 3,1 \big \rangle =\left \langle \dfrac{21}{5},\dfrac{7}{5}\right \rangle. \end{align*}\]

Now consider the vector \(\vecs{ q}=\vecs{ v}−\vecs{ p}.\) We have

\[\begin{align*} \vecs{ q} &=\vecs{ v}−\vecs{ p} \\[4pt]
&= \Big\langle 6,−4 \Big \rangle − \left \langle \dfrac{21}{5},\dfrac{7}{5} \right \rangle \\[4pt]
&= \left \langle \dfrac{9}{5},−\dfrac{27}{5}\right \rangle. \end{align*}\]

Clearly, by the way we defined \(\vecs{ q}\), we have \(\vecs{ v}=\vecs{ q}+\vecs{ p},\) and

\[\begin{align*}\vecs{ q}⋅\vecs{ p} &= \left \langle \dfrac{9}{5},−\dfrac{27}{5} \right \rangle ⋅ \left \langle \dfrac{21}{5},\dfrac{7}{5} \right \rangle \\[4pt]
&= \dfrac{9(21)}{25}+−\dfrac{27(7)}{25} \\[4pt]
&= \dfrac{189}{25}−\dfrac{189}{25}=0. \end{align*}\]

Therefore, \(\vecs{ q}\) and \(\vecs{ p}\) are orthogonal.

Example \(\PageIndex{6}\): Resolving Vectors into Components

Express \(\vecs{ v}=⟨8,−3,−3⟩\) as a sum of orthogonal vectors such that one of the vectors has the same direction as \(\vecs{ u}=⟨2,3,2⟩.\)

Solution

Let \(\vecs{ p}\) represent the projection of \(\vecs{ v}\) onto \(\vecs{ u}\):

\[ \begin{align*} \vecs{ p} =\text{proj}_\vecs{ u}\vecs{ v}  &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt]
&=\dfrac{⟨2,3,2⟩⋅⟨8,−3,−3⟩}{∥⟨2,3,2⟩∥^2} \left \langle 2,3,2 \right \rangle \\[4pt]
&=\dfrac{16−9−6}{2^2+3^2+2^2} \left \langle 2,3,2 \right \rangle =\dfrac{1}{17} \left \langle 2,3,2 \right \rangle = \left \langle \dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17} \right \rangle . \end{align*} \]

Then,

\[ \begin{align*} \vecs{ q} =\vecs{ v}−\vecs{ p} &=⟨8,−3,−3⟩− \left \langle \dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17} \right \rangle \\[4pt]
&= \left \langle \dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17} \right \rangle . \end{align*} \]

To check our work, we can use the dot product to verify that \(\vecs{ p}\) and \(\vecs{ q}\) are orthogonal vectors:

\[ \begin{align*}\vecs{ p}⋅\vecs{ q}&= \left \langle \dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17} \right \rangle ⋅⟨ \left \langle \dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17} \right \rangle \\[4pt]
&=\dfrac{268}{17}−\dfrac{162}{17}−\dfrac{106}{17}=0. \end{align*} \]

Then,

\[\vecs{ v}=\vecs{ p}+\vecs{ q}= \left \langle \dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17} \right \rangle + \left \langle \dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17} \right \rangle . \nonumber\]

 Try It \(\PageIndex{6}\)

Express \(\vecs{ v}=5\mathbf{\hat i}−\mathbf{\hat j}\) as a sum of orthogonal vectors such that one of the vectors has the same direction as \(\vecs{ u}=4\mathbf{\hat i}+2\mathbf{\hat j}\).

Hint

Start by finding the projection of \(\vecs{ v}\) onto \(\vecs{ u}\).

Answer

\(\vecs{ v}=\vecs{ p}+\vecs{ q},\) where \(\vecs{ p}=\dfrac{18}{5}\mathbf{\hat i}+\dfrac{9}{5}\mathbf{\hat j}\) and \(\vecs{ q}=\dfrac{7}{5}\mathbf{\hat i}−\dfrac{14}{5}\mathbf{\hat j}\)

Example \(\PageIndex{7}\): Scalar Projection of Velocity

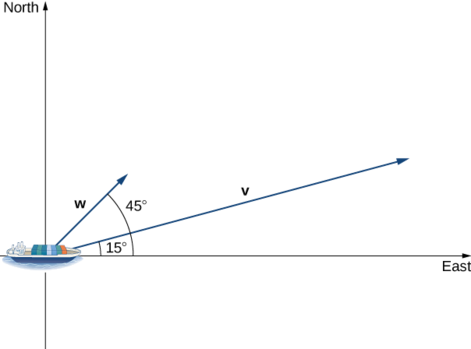A container ship leaves port traveling \(15°\) north of east. Its engine generates a speed of 20 knots along that path (see the following figure). In addition, the ocean current moves the ship northeast at a speed of 2 knots. Considering both the engine and the current, how fast is the ship moving in the direction \(15°\) north of east? Round the answer to two decimal places.

Solution

Let \(\vecs{ v}\) be the velocity vector generated by the engine, and let w be the velocity vector of the current. We already know \(‖\vecs{ v}‖=20\) along the desired route. We just need to add in the scalar projection of \(\vecs{ w}\) onto \(\vecs{ v}\). We get

\[ \begin{align*} \text{magnitude of projection }&=\dfrac{\vecs{ v}⋅\vecs{ w}}{‖\vecs{ v}‖} \\[4pt] &=\dfrac{‖\vecs{ v}‖‖\vecs{ w}‖\cos(30°)}{‖\vecs{ v}‖} [4pt] &=‖\vecs{ w}‖\cos(30°) =2\dfrac{\sqrt{3}}{2}=\sqrt{3}≈1.73\,\text{knots.}\end{align*}\]

The ship is moving at 21.73 knots in the direction \(15°\) north of east.

 Try It \(\PageIndex{7}\)

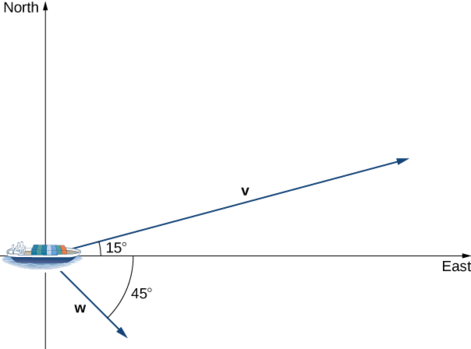Repeat the previous example, but assume the ocean current is moving southeast instead of northeast, as shown in the following figure.

 

 

Hint

Compute the scalar projection of \(\vecs{ w}\) onto \(\vecs{ v}\).

Answer

21 knots

Work

Now that we understand dot products, we can see how to apply them to real-life situations. The most common application of the dot product of two vectors is in the calculation of work.

From physics, we know that work is done when an object is moved by a force. When the force is constant and applied in the same direction the object moves, then we define the work done as the product of the force and the distance the object travels: \(W=Fd\). Now imagine the direction of the force is different from the direction of motion, as with the example of a child pulling a wagon. To find the work done, we need to multiply the component of the force that acts in the direction of the motion by the magnitude of the displacement. The dot product allows us to do just that. If we represent an applied force by a vector \(\vecs{ F}\) and the displacement of an object by a vector \(\vecs{ s}\), then the work done by the force is the dot product of \(\vecs{ F}\) and \(\vecs{ s}\).

Definition: Constant Force

When a constant force is applied to an object so the object moves in a straight line from point \(P\) to point \(Q\), the work \(W\) done by the force \(\vecs{ F}\), acting at an angle θ from the line of motion, is given by

\(W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ.\)

Let’s revisit the problem of the child’s wagon introduced earlier. Suppose a child is pulling a wagon with a force having a magnitude of 8 lb on the handle at an angle of 55°. If the child pulls the wagon 50 ft, find the work done by the force (Figure \(\PageIndex{8}\)).

Figure \(\PageIndex{8}\): The horizontal component of the force is the projection of \(\vecs{ F}\) onto the positive \(x\)-axis.

We have

\[W=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ=8(50)(\cos(55°))≈229\,\text{ft⋅lb.} \nonumber\]

In U.S. standard units, we measure the magnitude of force \(∥\vecs{ F}∥\) in pounds. The magnitude of the displacement vector \(∥\vecd{PQ}∥\) tells us how far the object moved, and it is measured in feet. The customary unit of measure for work, then, is the foot-pound. One foot-pound is the amount of work required to move an object weighing 1 lb a distance of 1 ft straight up. In the metric system, the unit of measure for force is the newton (N), and the unit of measure of magnitude for work is a newton-meter (N·m), or a joule (J).

Example \(\PageIndex{8}\): Calculating Work

A conveyor belt generates a force \(\vecs{ F}=5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k}\) that moves a suitcase from point \((1,1,1)\) to point \((9,4,7)\) along a straight line. Find the work done by the conveyor belt. The distance is measured in meters and the force is measured in newtons.

Solution

The displacement vector \(\vecd{PQ}\) has initial point \((1,1,1)\) and terminal point \((9,4,7)\):

\[\vecd{PQ}=⟨9−1,4−1,7−1⟩=⟨8,3,6⟩=8\mathbf{\hat i}+3\mathbf{\hat j}+6\mathbf{\hat k}. \nonumber\]

Work is the dot product of force and displacement:

\[\begin{align*} W &=\vecs{ F}⋅\vecd{PQ} \\[4pt]
&= (5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k})⋅(8\mathbf{\hat i}+3\mathbf{\hat j}+6\mathbf{\hat k}) \\[4pt]
&= 5(8)+(−3)(3)+1(6) \\[4pt] &=37\,\text{N⋅m} = 37\,\text{J} \end{align*}\]

 Try It \(\PageIndex{8}\)

A constant force of 30 lb is applied at an angle of 60° to pull a handcart 10 ft across the ground. What is the work done by this force?

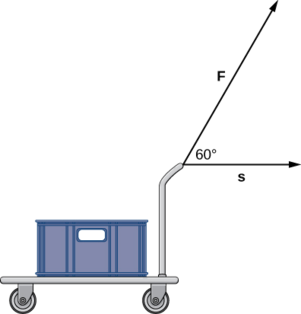
Hint

Use the definition of work as the dot product of force and distance.

Answer

150 ft-lb

Key Concepts

• The dot product, or scalar product, of two vectors \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) and \(\vecs{ v}=⟨v_1,v_2,v_3⟩\) is \(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\).
• The dot product of two vectors can be expressed, alternatively, as \(\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ.\) This form of the dot product is useful for finding the measure of the angle formed by two vectors.
• The cosine of the angle formed by \(\vecs{ u}\) and \(\vecs{ v}\) is \(\cos θ=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}\)
• The dot product satisfies the following properties:
  • \(\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u}\)
  • \(\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w}\)
  • \(c(\vecs{ u}⋅\vecs{ v})=(c\vecs{ u})⋅\vecs{ v}=\vecs{ u}⋅(c\vecs{ v})\)
  • \(\vecs{ v}⋅\vecs{ v}=‖\vecs{ v}‖^2\)
• Vectors \(\vecs{ u}\) and \(\vecs{ v}\) are orthogonal if \(\vecs{ u}⋅\vecs{ v}=0\).
• The vector projection of \(\vecs{ v}\) onto \(\vecs{ u}\) is the vector \(\text{proj}_{\vecs{ u}} \vecs{ v} = \dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}\).
• The magnitude of the vector projection is known as the scalar projection of \(\vecs{ v}\) onto \(\vecs{ u}\), given by \(\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}  = ‖\vecs{ v}‖ \cos θ  \).    
• Work is done when a force is applied to an object, causing displacement. When the force is represented by the vector \(\vecs{ F}\) and the displacement is represented by the vector \(\vecs{ s}\), then the work done \(W\) is given by the formula \(W=\vecs{ F}⋅\vecs{ s}=∥\vecs{ F}∥‖\vecs{ s}‖\cos θ.\)

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

• edited for vector notation by Paul Seeburger