4.E: Applications of Derivatives (ALL Chap 4 Exercises)
- Page ID
- 13620
These are homework exercises to accompany OpenStax's "Calculus" Textmap.
4.1: Related Rates
For the following exercises, find the quantities for the given equation.
1) Find \(\frac{dy}{dt}\) at \(x=1\) and \(y=x^2+3\) if \(\frac{dx}{dt}=4.\)
Solution: \(8\)
2) Find \(\frac{dx}{dt}\) at \(x=−2\) and \(y=2x^2+1\) if \(\frac{dy}{dt}=−1.\)
3) Find \(\frac{dz}{dt}\) at \((x,y)=(1,3)\) and \(z^2=x^2+y^2\) if \(\frac{dx}{dt}=4\) and \(\frac{dy}{dt}=3\).
Solution: \(\frac{13}{\sqrt{10}}\)
For the following exercises, sketch the situation if necessary and used related rates to solve for the quantities.
4) [T] If two electrical resistors are connected in parallel, the total resistance (measured in ohms, denoted by the Greek capital letter omega, \(Ω\)) is given by the equation \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}.\) If \(R_1\) is increasing at a rate of \(0.5Ω/min\) and \(R_2\) decreases at a rate of \(1.1Ω/min\), at what rate does the total resistance change when \(R_1=20Ω\) and \(R_2=50Ω/min\)?
5) A 10-ft ladder is leaning against a wall. If the top of the ladder slides down the wall at a rate of 2 ft/sec, how fast is the bottom moving along the ground when the bottom of the ladder is 5 ft from the wall?
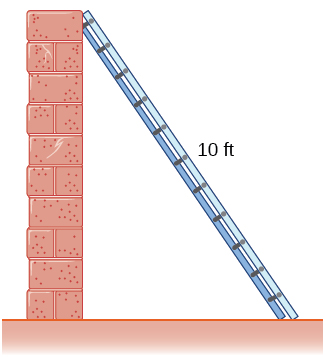
Solution: \(2\sqrt{3} ft/sec\)
6) A 25-ft ladder is leaning against a wall. If we push the ladder toward the wall at a rate of 1 ft/sec, and the bottom of the ladder is initially \(20ft\) away from the wall, how fast does the ladder move up the wall \(5sec\) after we start pushing?
7) Two airplanes are flying in the air at the same height: airplane A is flying east at 250 mi/h and airplane B is flying north at \(300mi/h.\) If they are both heading to the same airport, located 30 miles east of airplane A and 40 miles north of airplane B, at what rate is the distance between the airplanes changing?
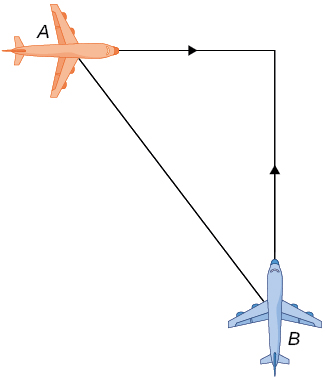
Solution: The distance is decreasing at \(390mi/h.\)
8) You and a friend are riding your bikes to a restaurant that you think is east; your friend thinks the restaurant is north. You both leave from the same point, with you riding at 16 mph east and your friend riding \(12mph\) north. After you traveled \(4mi,\) at what rate is the distance between you changing?
9) Two buses are driving along parallel freeways that are \(5mi\) apart, one heading east and the other heading west. Assuming that each bus drives a constant \(55mph\), find the rate at which the distance between the buses is changing when they are \(13mi\) part, heading toward each other.
Solution: The distance between them shrinks at a rate of \(\frac{1320}{13}≈101.5mph.\)
10) A 6-ft-tall person walks away from a 10-ft lamppost at a constant rate of \(3ft/sec.\) What is the rate that the tip of the shadow moves away from the pole when the person is 10ft away from the pole?
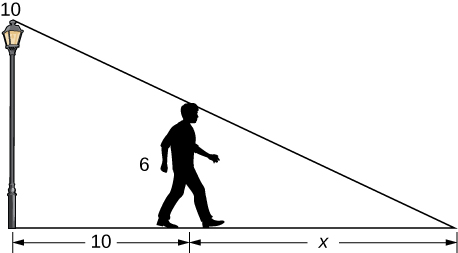
Using the previous problem, what is the rate at which the tip of the shadow moves away from the person when the person is 10 ft from the pole?
Solution: \(\frac{9}{2} ft/sec\)
11) A 5-ft-tall person walks toward a wall at a rate of 2 ft/sec. A spotlight is located on the ground 40 ft from the wall. How fast does the height of the person’s shadow on the wall change when the person is 10 ft from the wall?
12) Using the previous problem, what is the rate at which the shadow changes when the person is 10 ft from the wall, if the person is walking away from the wall at a rate of 2 ft/sec?
Solution: It grows at a rate \(\frac{4}{9}\) ft/sec
13) A helicopter starting on the ground is rising directly into the air at a rate of 25 ft/sec. You are running on the ground starting directly under the helicopter at a rate of 10 ft/sec. Find the rate of change of the distance between the helicopter and yourself after 5 sec.
Solution: The distance is increasing at \((\frac{135\sqrt{26})}{26}\) ft/sec
14) For the following exercises, draw and label diagrams to help solve the related-rates problems.
The side of a cube increases at a rate of \(\frac{1}{2}\) m/sec. Find the rate at which the volume of the cube increases when the side of the cube is 4 m.
The volume of a cube decreases at a rate of \(10\) m/sec. Find the rate at which the side of the cube changes when the side of the cube is 2 m.
Slution: \(−\frac{5}{6}\) m/sec
15) The radius of a circle increases at a rate of \(2\) m/sec. Find the rate at which the area of the circle increases when the radius is 5 m.
16) The radius of a sphere decreases at a rate of \(3\) m/sec. Find the rate at which the surface area decreases when the radius is 10 m.
Solution: \(240π m^2/sec\)
17) The radius of a sphere increases at a rate of 1 m/sec. Find the rate at which the volume increases when the radius is \(20\) m.
18) The radius of a sphere is increasing at a rate of 9 cm/sec. Find the radius of the sphere when the volume and the radius of the sphere are increasing at the same numerical rate.
Solution: \(\frac{1}{2\sqrt{π}}\) cm
19) The base of a triangle is shrinking at a rate of 1 cm/min and the height of the triangle is increasing at a rate of 5 cm/min. Find the rate at which the area of the triangle changes when the height is 22 cm and the base is 10 cm.
20) A triangle has two constant sides of length 3 ft and 5 ft. The angle between these two sides is increasing at a rate of 0.1 rad/sec. Find the rate at which the area of the triangle is changing when the angle between the two sides is \(π/6.\)
Solution: The area is increasing at a rate \(\frac{(3\sqrt{3})}{8}ft_2/sec.\)
21) A triangle has a height that is increasing at a rate of 2 cm/sec and its area is increasing at a rate of 4 \(cm^2/sec\). Find the rate at which the base of the triangle is changing when the height of the triangle is 4 cm and the area is 20 \(cm^2\).
For the following exercises, consider a right cone that is leaking water. The dimensions of the conical tank are a height of 16 ft and a radius of 5 ft.
22) How fast does the depth of the water change when the water is 10 ft high if the cone leaks water at a rate of 10 \(ft^3/min\)?
Solution: The depth of the water decreases at \(\frac{128}{125π}\) ft/min.
23) Find the rate at which the surface area of the water changes when the water is 10 ft high if the cone leaks water at a rate of 10 \(ft^3/min\).
24) If the water level is decreasing at a rate of 3 in./min when the depth of the water is 8 ft, determine the rate at which water is leaking out of the cone.
Solution: The volume is decreasing at a rate of \(\frac{(25π)}{16}ft^3/min.\)
25) A vertical cylinder is leaking water at a rate of 1 \(ft^3/sec\). If the cylinder has a height of 10 ft and a radius of 1 ft, at what rate is the height of the water changing when the height is 6 ft?
26) A cylinder is leaking water but you are unable to determine at what rate. The cylinder has a height of 2 m and a radius of 2 m. Find the rate at which the water is leaking out of the cylinder if the rate at which the height is decreasing is 10 cm/min when the height is 1 m.
Solution: The water flows out at rate \(\frac{(2π)}{5}m_3/min.\)
27) A trough has ends shaped like isosceles triangles, with width 3 m and height 4 m, and the trough is 10 m long. Water is being pumped into the trough at a rate of \(5m^3/min\). At what rate does the height of the water change when the water is 1 m deep?
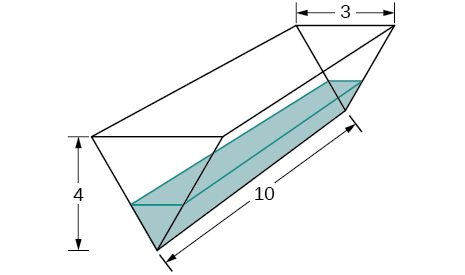
28) A tank is shaped like an upside-down square pyramid, with base of 4 m by 4 m and a height of 12 m (see the following figure). How fast does the height increase when the water is 2 m deep if water is being pumped in at a rate of \(\frac{2}{3}\) m/sec?
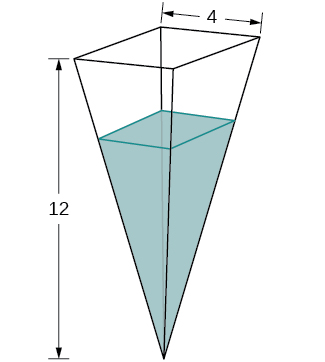
Solution: \(\frac{3}{2} m/sec\)
For the following problems, consider a pool shaped like the bottom half of a sphere, that is being filled at a rate of 25 \(ft^3\)/min. The radius of the pool is 10 ft.
29) Find the rate at which the depth of the water is changing when the water has a depth of 5 ft.
30) Find the rate at which the depth of the water is changing when the water has a depth of 1 ft.
Solution: \(\frac{25}{19π} ft/min\)
31) If the height is increasing at a rate of 1 in./sec when the depth of the water is 2 ft, find the rate at which water is being pumped in.
32) Gravel is being unloaded from a truck and falls into a pile shaped like a cone at a rate of 10 \(ft^3/min\). The radius of the cone base is three times the height of the cone. Find the rate at which the height of the gravel changes when the pile has a height of 5 ft.
Solution: \(\frac{2}{45π} ft/min\)
33) Using a similar setup from the preceding problem, find the rate at which the gravel is being unloaded if the pile is 5 ft high and the height is increasing at a rate of 4 in./min.
For the following exercises, draw the situations and solve the related-rate problems.
34) You are stationary on the ground and are watching a bird fly horizontally at a rate of \(10\) m/sec. The bird is located 40 m above your head. How fast does the angle of elevation change when the horizontal distance between you and the bird is 9 m?
Solution: The angle decreases at \(\frac{400}{1681}rad/sec.\)
35) You stand 40 ft from a bottle rocket on the ground and watch as it takes off vertically into the air at a rate of 20 ft/sec. Find the rate at which the angle of elevation changes when the rocket is 30 ft in the air.
36) A lighthouse, L, is on an island 4 mi away from the closest point, P, on the beach (see the following image). If the lighthouse light rotates clockwise at a constant rate of 10 revolutions/min, how fast does the beam of light move across the beach 2 mi away from the closest point on the beach?
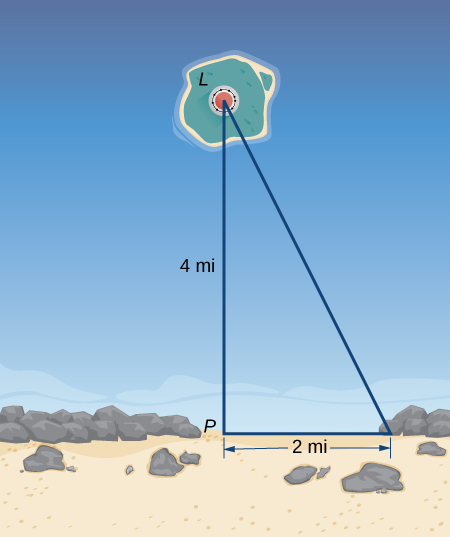
Solution: \(100π/min\)
37)Using the same setup as the previous problem, determine at what rate the beam of light moves across the beach 1 mi away from the closest point on the beach.
38) You are walking to a bus stop at a right-angle corner. You move north at a rate of 2 m/sec and are 20 m south of the intersection. The bus travels west at a rate of 10 m/sec away from the intersection – you have missed the bus! What is the rate at which the angle between you and the bus is changing when you are 20 m south of the intersection and the bus is 10 m west of the intersection?
Solution: The angle is changing at a rate of \(\frac{21}{25}rad/sec\).
For the following exercises, refer to the figure of baseball diamond, which has sides of 90 ft.
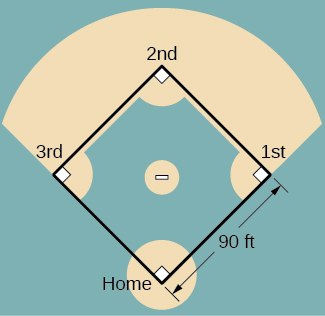
39) [T] A batter hits a ball toward third base at 75 ft/sec and runs toward first base at a rate of 24 ft/sec. At what rate does the distance between the ball and the batter change when 2 sec have passed?
40) [T] A batter hits a ball toward second base at 80 ft/sec and runs toward first base at a rate of 30 ft/sec. At what rate does the distance between the ball and the batter change when the runner has covered one-third of the distance to first base? (Hint: Recall the law of cosines.)
Solution: The distance is increasing at a rate of \(62.50\) ft/sec.
41) [T] A batter hits the ball and runs toward first base at a speed of 22 ft/sec. At what rate does the distance between the runner and second base change when the runner has run 30 ft?
42) [T] Runners start at first and second base. When the baseball is hit, the runner at first base runs at a speed of 18 ft/sec toward second base and the runner at second base runs at a speed of 20 ft/sec toward third base. How fast is the distance between runners changing 1 sec after the ball is hit?
Solution: The distance is decreasing at a rate of \(11.99\) ft/sec.
4.2: Linear Approximations and Differentials
1) What is the linear approximation for any generic linear function \(y=mx+b\)?
2) Determine the necessary conditions such that the linear approximation function is constant. Use a graph to prove your result.
Solution: \(f′(a)=0\)
3) Explain why the linear approximation becomes less accurate as you increase the distance between \(x\) and \(a\). Use a graph to prove your argument.
4) When is the linear approximation exact?
Solution: The linear approximation exact when \(y=f(x)\) is linear or constant.
For the following exercises, find the linear approximation \(L(x)\) to \(y=f(x)\) near \(x=a\) for the function.
5) [T] \(f(x)=x+x^4,a=0\)
6) [T] \(f(x)=\frac{1}{x},a=2\)
Solution: \(L(x)=\frac{1}{2}−\frac{1}{4}(x−2)\)
7) [T] \(f(x)=tanx,a=\frac{π}{4}\)
8) [T] \(f(x)=sinx,a=\frac{π}{2}\)
Solution: \(L(x)=1\)
9) [T] \(f(x)=xsinx,a=2π\)
10) [T] \(f(x)=sin^2x,a=0\)
Solution: \(L(x)=0\)
For the following exercises, compute the values given within 0.01 by deciding on the appropriate \(f(x)\) and \(a\), and evaluating \(L(x)=f(a)+f′(a)(x−a).\) Check your answer using a calculator.
11) [T] \((2.001)^6\)
12) [T] \(sin(0.02)\)
Solution: \(0.02\)
13) [T] \(cos(0.03)\)
14) [T] \((15.99)^{1/4}\)
Solution: \(1.9996875\)
15) [T] \(\frac{1}{0.98}\)
16) [T] \(sin(3.14)\)
Solution: \(0.001593\)
For the following exercises, determine the appropriate \(f(x)\) and \(a\), and evaluate \(L(x)=f(a)+f′(a)(x−a).\) Calculate the numerical error in the linear approximations that follow.
17) \((1.01)^3\)
18) \(cos(0.01)\)
Solution: \(1;\) error, \(~0.00005\)
19) \((sin(0.01))^2\)
20) \((1.01)^{−3}\)
Solution: \(0.97;\) error, \(~0.0006\)
21) \((1+\frac{1}{10})^{10}\)
22) \(\sqrt{8.99}\)
Solution: \(3−\frac{1}{600};\) error, \(~4.632×10^{−7}\)
For the following exercises, find the differential of the function.
23) \(y=3x^4+x^2−2x+1\)
24) \(y=xcosx\)
Solution: \(dy=(cosx−xsinx)dx\)
25) \(y=\sqrt{1+x}\)
26) \(y=\frac{x^2+2}{x−1}\)
Solution: \(dy=(\frac{x^2−2x−2}{(x−1)^2})dx\)
For the following exercises, find the differential and evaluate for the given \(x\) and \(dx\).
27) \(y=3x^2−x+6, x=2, dx=0.1\)
28) \(y=\frac{1}{x+1},x=1, dx=0.25\)
Solution: \(dy=−\frac{1}{(x+1)^2}dx,−\frac{1}{16}\)
29) \(y=tanx,x=0, dx=\frac{π}{10}\)
30) \(y=\frac{3x^2+2}{\sqrt{x+1}}\), x=0, dx=0.1\)
Solution: \(dy=\frac{9x^2+12x−2}{2(x+1)^{3/2}}dx,−0.1\)
31) \(y=\frac{sin(2x)}{x}, x=π, dx=0.25\)
32) \(y=x^3+2x+\frac{1}{x}, x=1, dx=0.05\)
Solution: \(dy=(3x^2+2−\frac{1}{x^2})dx, 0.2\)
For the following exercises, find the change in volume \(dV\) or in surface area \(dA.\)
33) \(dV\) if the sides of a cube change from 10 to 10.1.
34) \(dA\) if the sides of a cube change from \(x\) to \(x+dx\).
Solution: \(12xdx\)
35) \(dA\) if the radius of a sphere changes from \(r\) by \(dr.\)
36) \(dV\) if the radius of a sphere changes from \(r\) by \(dr\).
Solution: \(4πr^2dr\)
37) \(dV\) if a circular cylinder with \(r=2\) changes height from 3 cm to \(3.05cm.\)
38) \(dV\) if a circular cylinder of height 3 changes from \(r=2\) to \(r=1.9cm.\)
Solution: \(−1.2πcm^3\)
For the following exercises, use differentials to estimate the maximum and relative error when computing the surface area or volume.
39) A spherical golf ball is measured to have a radius of \(5mm,\) with a possible measurement error of \(0.1mm.\) What is the possible change in volume?
40) A pool has a rectangular base of 10 ft by 20 ft and a depth of 6 ft. What is the change in volume if you only fill it up to 5.5 ft?
Solution: \(−100 ft^3\)
41) An ice cream cone has height 4 in. and radius 1 in. If the cone is 0.1 in. thick, what is the difference between the volume of the cone, including the shell, and the volume of the ice cream you can fit inside the shell
For the following exercises, confirm the approximations by using the linear approximation at \(x=0.\)
42) \(\sqrt{1−x}≈1−\frac{1}{2}x\)
43) \(\frac{1}{\sqrt{1−x^2}}≈1\)
44) \(\sqrt{c^2+x^2}≈c\)
4.3: Maxima and Minima
1) In precalculus, you learned a formula for the position of the maximum or minimum of a quadratic equation \(y=ax^2+bx+c\), which was \(m=−\frac{b}{(2a)}\). Prove this formula using calculus.
2) If you are finding an absolute minimum over an interval \([a,b],\) why do you need to check the endpoints? Draw a graph that supports your hypothesis.
Solution: Answers may vary
3) If you are examining a function over an interval \((a,b),\) for \(a\) and \(b\) finite, is it possible not to have an absolute maximum or absolute minimum?
4) When you are checking for critical points, explain why you also need to determine points where \(f(x)\) is undefined. Draw a graph to support your explanation.
Solution: Answers will vary
5) Can you have a finite absolute maximum for \(y=ax^2+bx+c\) over \((−∞,∞)\)? Explain why or why not using graphical arguments.
6) Can you have a finite absolute maximum for \(y=ax^3+bx^2+cx+d\) over \((−∞,∞)\) assuming a is non-zero? Explain why or why not using graphical arguments.
Solution: No; answers will vary
7) Let \(m\) be the number of local minima and \(M\) be the number of local maxima. Can you create a function where \(M>m+2\)? Draw a graph to support your explanation.
8) Is it possible to have more than one absolute maximum? Use a graphical argument to prove your hypothesis.
Solution: Since the absolute maximum is the function (output) value rather than the x value, the answer is no; answers will vary
9) Is it possible to have no absolute minimum or maximum for a function? If so, construct such a function. If not, explain why this is not possible.
10) [T] Graph the function \(y=e^{ax}.\) For which values of \(a\), on any infinite domain, will you have an absolute minimum and absolute maximum?
Solution: When \(a=0\)
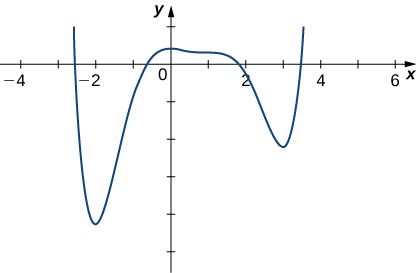
For the following exercises, determine where the local and absolute maxima and minima occur on the graph given. Assume domains are closed intervals unless otherwise specified.
11)
12)
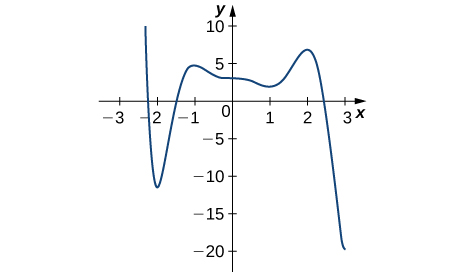
Solution: Absolute minimum at 3; Absolute maximum at −2.2; local minima at −2, 1; local maxima at −1, 2
13)
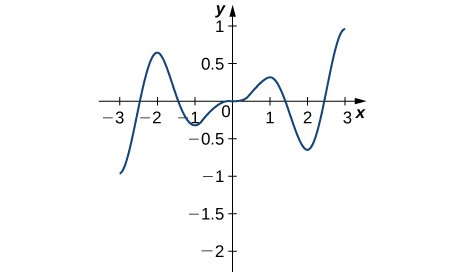
14)
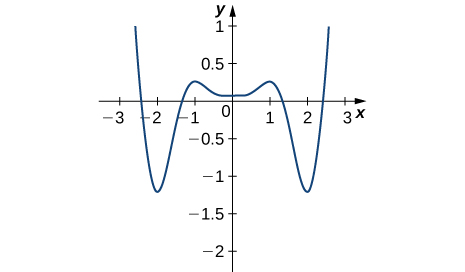
Solution: Absolute minima at −2, 2; absolute maxima at −2.5, 2.5; local minimum at 0; local maxima at −1, 1
For the following problems, draw graphs of \(f(x),\) which is continuous, over the interval \([−4,4]\) with the following properties:
15) Absolute maximum at \(x=2\) and absolute minima at \(x=±3\)
16) Absolute minimum at \(x=1\) and absolute maximum at \(x=2\)
Solution: Answers may vary.
17) Absolute maximum at \(x=4,\) absolute minimum at \(x=−1,\) local maximum at \(x=−2,\) and a critical point that is not a maximum or minimum at \(x=2\)
18) Absolute maxima at \(x=2\) and \(x=−3\), local minimum at \(x=1\), and absolute minimum at \(x=4\)
Solution: Answers may vary.
For the following exercises, find the critical points in the domains of the following functions.
19) \(y=4x^3−3x\)
20) \(y=4\sqrt{x}−x^2\)
Solution: \(x=1\)
21) \(y=\frac{1}{x−1}\)
22) \(y=ln(x−2)\)
Solution: None
23) \(y=tan(x)\)
24) \(y=\sqrt{4−x^2}\)
Solution: \(x=0\)
25) \(y=x^{3/2}−3x^{5/2}\)
26) \(y=\frac{x^2−1}{x^2+2x−3}\)
Solution: None
27) \(y=sin^2(x)\)
28) \(y=x+\frac{1}{x}\)
Solution: \(x=−1,1\)
For the following exercises, find the local and/or absolute maxima for the functions over the specified domain.
29) \(f(x)=x2^+3\) over \([−1,4]\)
30) \(y=x^2+\frac{2}{x}\) over \([1,4]\)
Solution: Absolute maximum: \(x=4, y=\frac{33}{2}\); absolute minimum: \(x=1, y=3\)
31) \(y=(x−x^2)^2\) over \([−1,1]\)
32) \(y=\frac{1}{(x−x^2)}\) over \([0,1]\)
Solution: Absolute minimum: \(x=\frac{1}{2}, y=4\)
33) \(y=\sqrt{9−x}\) over \([1,9]\)
34) \(y=x+sin(x)\) over \([0,2π]\)
Solution: Absolute maximum: \(x=2π, y=2π;\) absolute minimum: \(x=0, y=0\)
35) \(y=\frac{x}{1+x}\) over \([0,100]\)
36) \(y=|x+1|+|x−1|\) over \([−3,2]\)
Solution: Absolute maximum: \(x=−3;\) absolute minimum: \(−1≤x≤1, y=2\)
37) \(y=\sqrt{x}−\sqrt{x^3}\) over \([0,4]\)
38) \(y=sinx+cosx\) over \([0,2π]\)
Solution: Absolute maximum: \(x=\frac{π}{4}, y=\sqrt{2}\); absolute minimum: \(x=\frac{5π}{4}, y=−\sqrt{2}\)
39) \(y=4sinθ−3cosθ\) over \([0,2π]\)
For the following exercises, find the local and absolute minima and maxima for the functions over \((−∞,∞).\)
40) \(y=x^2+4x+5\)
Solution: Absolute minimum: \(x=−2, y=1\)
41) \(y=x^3−12x\)
42) \(y=3x^4+8x^3−18x^2\)
Solution: Absolute minimum: \(x=−3, y=−135;\) local maximum: \(x=0, y=0\); local minimum: \(x=1, y=−7\)
43) \(y=x^3(1−x)^6\)
44) \(y=\frac{x^2+x+6}{x−1}\)
Solution: Local maximum: \(x=1−2\sqrt{2}, y=3−4\sqrt{2}\); local minimum: \(x=1+2\sqrt{2}, y=3+4\sqrt{2}\)
45) \(y=\frac{x^2−1}{x−1}\)
For the following functions, use a calculator to graph the function and to estimate the absolute and local maxima and minima. Then, solve for them explicitly.
46) [T] \(y=3x\sqrt{1−x^2}\)
Solution: Absolute maximum: \(x=\frac{\sqrt{2}}{2}, y=\frac{3}{2};\) absolute minimum: \(x=−\frac{\sqrt{2}}{2}, y=−\frac{3}{2}\)
47) [T] \(y=x+sin(x)\)
48) [T] \(y=12x^5+45x^4+20x^3−90x^2−120x+3\)
Solution: Local maximum: \(x=−2,y=59\); local minimum: \(x=1, y=−130\)
49) [T] \(y=\frac{x^3+6x^2−x−30}{x−2}\)
50) [T] \(y=\frac{\sqrt{4−x^2}}{\sqrt{4+x^2}}\)
Solution: Absolute maximum: \(x=0, y=1;\) absolute minimum: \(x=−2,2, y=0\)
51) A company that produces cell phones has a cost function of \(C=x^2−1200x+36,400,\) where \(C\) is cost in dollars and \(x\) is number of cell phones produced (in thousands). How many units of cell phone (in thousands) minimizes this cost function?
52) A ball is thrown into the air and its position is given by \(h(t)=−4.9t^2+60t+5m.\) Find the height at which the ball stops ascending. How long after it is thrown does this happen?
Solution: \(h=\frac{9245}{49}m, t=\frac{300}{49}s\)
For the following exercises, consider the production of gold during the California gold rush (1848–1888). The production of gold can be modeled by \(G(t)=\frac{(25t)}{(t^2+16)}\), where t is the number of years since the rush began \((0≤t≤40)\) and \(G\) is ounces of gold produced (in millions). A summary of the data is shown in the following figure.
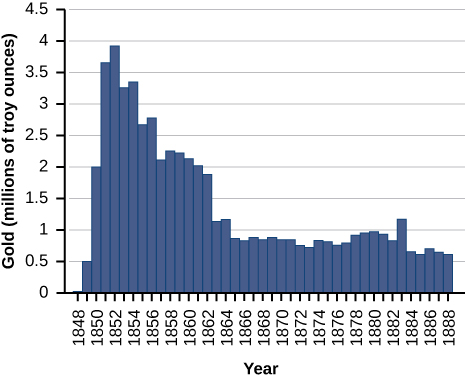
53) Find when the maximum (local and global) gold production occurred, and the amount of gold produced during that maximum.
54) Find when the minimum (local and global) gold production occurred. What was the amount of gold produced during this minimum?
Solution: The global minimum was in 1848, when no gold was produced.
Find the critical points, maxima, and minima for the following piecewise functions.
55) \(y=\begin{cases}x^2−4x& 0≤x≤1//x^2−4&1<x≤2\end{cases}\)
56) \(y=\begin{cases}x^2+1 & x≤1 // x^2−4x+5 & x>1\end{cases}\)
Solution: Absolute minima: \(x=0, x=2, y=1\); local maximum at \(x=1, y=2\)
For the following exercises, find the critical points of the following generic functions. Are they maxima, minima, or neither? State the necessary conditions.
57) \(y=ax^2+bx+c,\) given that \(a>0\)
58) \(y=(x−1)^a\), given that \(a>1\)
Solution: No maxima/minima if \(a\) is odd, minimum at \(x=1\) if \(a\) is even
4.4: The Mean Value Theorem
1)Why do you need continuity to apply the Mean Value Theorem? Construct a counterexample.
2) Why do you need differentiability to apply the Mean Value Theorem? Find a counterexample.
Solution: One example is \(f(x)=|x|+3,−2≤x≤2\)
3) When are Rolle’s theorem and the Mean Value Theorem equivalent?
4) If you have a function with a discontinuity, is it still possible to have \(f′(c)(b−a)=f(b)−f(a)?\) Draw such an example or prove why not.
Solution: Yes, but the Mean Value Theorem still does not apply
For the following exercises, determine over what intervals (if any) the Mean Value Theorem applies. Justify your answer.
5) \(y=sin(πx)\)
6) \(y=\frac{1}{x^3}\)
Solution: \((−∞,0),(0,∞)\)
7) \(y=\sqrt{4−x^2}\)
8) \(y=\sqrt{x^2−4}\)
Solution: \((−∞,−2),(2,∞)\)
9) \(y=ln(3x−5)\)
For the following exercises, graph the functions on a calculator and draw the secant line that connects the endpoints. Estimate the number of points \(c\) such that \(f′(c)(b−a)=f(b)−f(a).\)
10) [T] \(y=3x^3+2x+1\) over \([−1,1]\)
Solution: 2 points
11) [T] \(y=tan(\frac{π}{4}x)\) over \([−\frac{3}{2},\frac{3}{2}]\)
12) [T] \(y=x^2cos(πx)\) over \([−2,2]\)
Solution: 5 points
13) [T] \(y=x^6−\frac{3}{4}x^5−\frac{9}{8}x^4+\frac{15}{16}x^3+\frac{3}{32}x^2+\frac{3}{16}x+\frac{1}{32}\) over \([−1,1]\)
For the following exercises, use the Mean Value Theorem and find all points \(0<c<2\) such that \(f(2)−f(0)=f′(c)(2−0)\).
14) \(f(x)=x^3\)
Solution: \(c=\frac{2\sqrt{3}}{3}\)
15) \(f(x)=sin(πx)\)
16) \(f(x)=cos(2πx)\)
Solution: \(c=\frac{1}{2},1,\frac{3}{2}\)
17) \(f(x)=1+x+x^2\)
18) \(f(x)=(x−1)^{10}\)
Solution: \(c=1\)
19) \(f(x)=(x−1)^9\)
For the following exercises, show there is no \(c\) such that \(f(1)−f(−1)=f′(c)(2)\). Explain why the Mean Value Theorem does not apply over the interval \([−1,1].\)
20) \(f(x)=∣x−\frac{1}{2} ∣\)
Solution: Not differentiable
21) \(f(x)=\frac{1}{x^2}\)
22) \(f(x)=\sqrt{|x|}\)
Solution: Not differentiable
23) \(f(x)=[x]\) (Hint: This is called the floor function and it is defined so that \(f(x)\) is the largest integer less than or equal to \(x\).)
For the following exercises, determine whether the Mean Value Theorem applies for the functions over the given interval \(([a,b]\. Justify your answer.
24) \(y=e^x\) over \([0,1]\)
Solution: Yes
25) \(y=ln(2x+3)\) over \([−\frac{3}{2},0]\)
26) \(f(x)=tan(2πx)\) over \([0,2]\)
Solution: The Mean Value Theorem does not apply since the function is discontinuous at \(x=\frac{1}{4},\frac{3}{4},\frac{5}{4},\frac{7}{4}.\)
27) \(y=\sqrt{9−x^2}\) over \([−3,3]\)
28) \(y=\frac{1}{|x+1|}\) over \([0,3]\)
Solution: Yes
29) \(y=x^3+2x+1\) over \([0,6]\)
30) \(y=\frac{x^2+3x+2}{x}\) over \([−1,1]\)
Solution: The Mean Value Theorem does not apply; discontinuous at \(x=0.\)
31) \(y=\frac{x}{sin(πx)+1}\) over \([0,1]\)
32) \(y=ln(x+1)\) over \([0,e−1]\)
Yes
33) \(y=xsin(πx)\) over \([0,2]\)
34) \(y=5+|x|\) over \([−1,1]\)
Solution: The Mean Value Theorem does not apply; not differentiable at \(x=0\).
For the following exercises, consider the roots of the equation.
35) Show that the equation \(y=x^3+3x^2+16\) has exactly one real root. What is it?
36) Find the conditions for exactly one root (double root) for the equation \(y=x^2+bx+c\)
Solution: \(b=±2\sqrt{c}\)
37) Find the conditions for \(y=e^x−b\) to have one root. Is it possible to have more than one root?
For the following exercises, use a calculator to graph the function over the interval \([a,b]\) and graph the secant line from \(a\) to \(b\). Use the calculator to estimate all values of \(c\) as guaranteed by the Mean Value Theorem. Then, find the exact value of \(c\), if possible, or write the final equation and use a calculator to estimate to four digits.
38) [T] \(y=tan(πx)\) over \([−\frac{1}{4},\frac{1}{4}]\)
Solution: \(c=±\frac{1}{π}cos^{−1}(\frac{\sqrt{π}}{2}), c=±0.1533\)
39) [T] \(y=\frac{1}{\sqrt{x+1}}\) over \([0,3]\)
40) [T] \(y=∣x^2+2x−4∣\) over \([−4,0]\)
Solution: The Mean Value Theorem does not apply.
41) [T] \(y=x+\frac{1}{x}\) over \([\frac{1}{2},4]\)
42) [T] \(y=\sqrt{x+1}+\frac{1}{x^2}\) over \([3,8]\)
Solution: \(\frac{1}{2\sqrt{c+1}}−\frac{2}{c^3}=\frac{521}{2880}; c=3.133,5.867\)
43) At 10:17 a.m., you pass a police car at 55 mph that is stopped on the freeway. You pass a second police car at 55 mph at 10:53 a.m., which is located 39 mi from the first police car. If the speed limit is 60 mph, can the police cite you for speeding?
44) Two cars drive from one spotlight to the next, leaving at the same time and arriving at the same time. Is there ever a time when they are going the same speed? Prove or disprove.
Solution: Yes
45) Show that \(y=sec^2x\) and \(y=tan^2x\) have the same derivative. What can you say about \(y=sec^2x−tan^2x\)?
46) Show that \(y=csc^2x\) and \(y=cot^2x\) have the same derivative. What can you say about \(y=csc^2x−cot^2x\)?
Solution: It is constant.
4.5: Derivatives and the Shape of a Graph
1) If c is a critical point of \(f(x)\), when is there no local maximum or minimum at \(c\)? Explain.
2) For the function \(y=x^3\), is \(x=0\) both an inflection point and a local maximum/minimum?
Solution: It is not a local maximum/minimum because \(f′\) does not change sign
3) For the function \(y=x^3\), is \(x=0\) an inflection point?
4) Is it possible for a point \(c\) to be both an inflection point and a local extrema of a twice differentiable function?
Solution: No
6) Why do you need continuity for the first derivative test? Come up with an example.
7) Explain whether a concave-down function has to cross \(y=0\) for some value of \(x\).
Solution: False; for example, \(y=\sqrt{x}\).
8) Explain whether a polynomial of degree \(2\) can have an inflection point.
For the following exercises, analyze the graphs of \(f′\), then list all intervals where f is increasing or decreasing.
9)
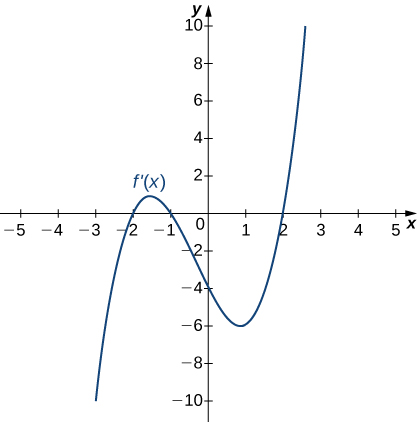
Solution: Increasing for \(−2<x<−1\) and \(x>2\); decreasing for \(x<−2\) and \(−1<x<2\)
10)
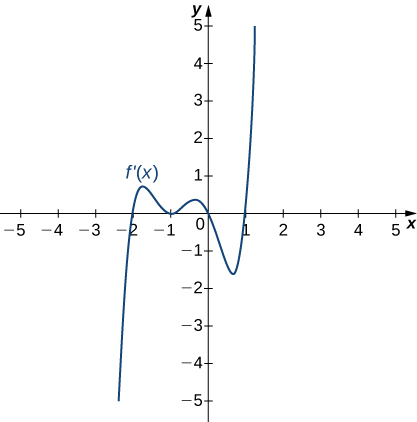
11)
Solution: Decreasing for \(x<1\), increasing for \(x>1\)
12)
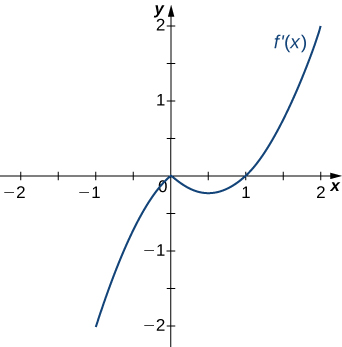
13)
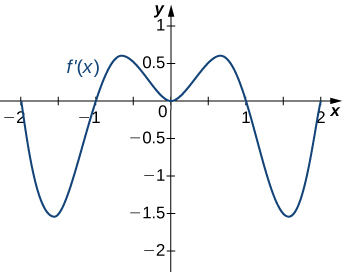
Solution: Decreasing for \(−2<x<−1\) and \(1<x<2\); increasing for \(−1<x<1\) and \(x<−2\) and \(x>2\)
For the following exercises, analyze the graphs of \(f′,\) then list all intervals where
a. \(f\) is increasing and decreasing and
b. the minima and maxima are located.
14)
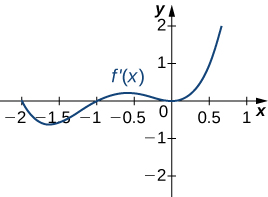
15)
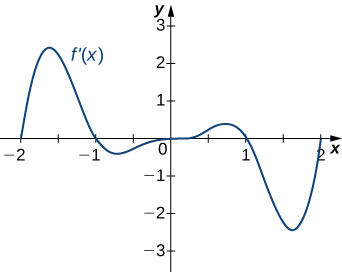
Solution: a. Increasing over \(−2<x<−1,0<x<1,x>2\), decreasing over \(x<−2, −1<x<0,1<x<2;\) b. maxima at \(x=−1\) and \(x=1\), minima at \(x=−2\) and \(x=0\) and \(x=2\)
16)
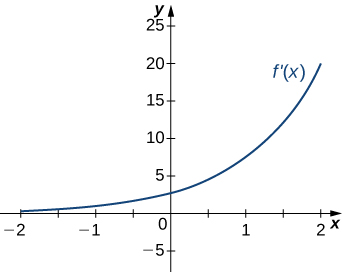
17)
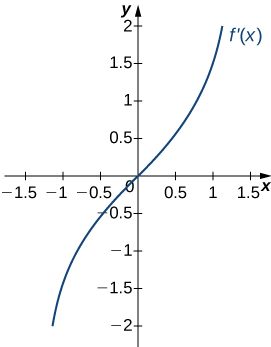
Solution: a. Increasing over \(x>0\), decreasing over \(x<0;\) b. Minimum at \(x=0\)
18)
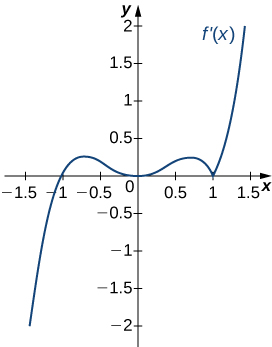
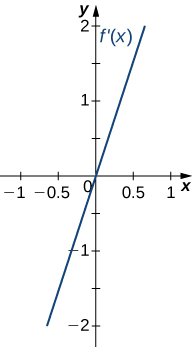
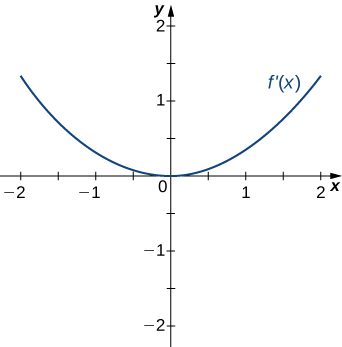
For the following exercises, analyze the graphs of \(f′\), then list all inflection points and intervals \(f\) that are concave up and concave down.
19)
Solution: Concave up on all \(x\), no inflection points
20)
21)
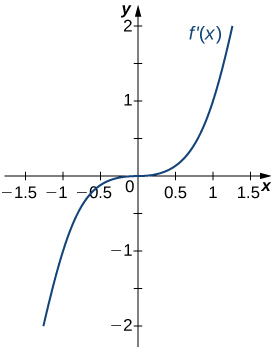
Solution: Concave up on all \(x\), no inflection points
22)
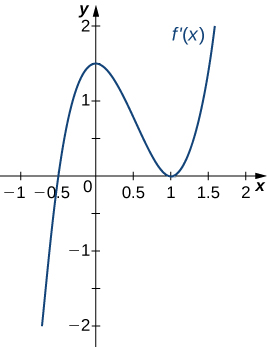
23)
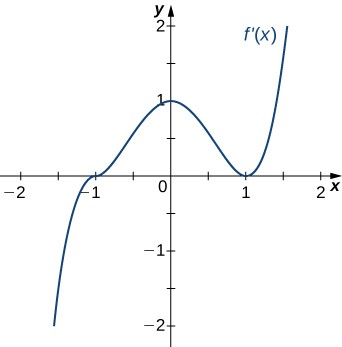
Solution: Concave up for \(x<0\) and \(x>1\), concave down for \(0<x<1\), inflection points at \(x=0\) and \(x=1\)
For the following exercises, draw a graph that satisfies the given specifications for the domain \(x=[−3,3].\) The function does not have to be continuous or differentiable.
24) \(f(x)>0,f′(x)>0\) over \(x>1,−3<x<0,f′(x)=0\) over \(0<x<1\)
25) \(f′(x)>0\) over \(x>2,−3<x<−1,f′(x)<0\) over \(−1<x<2,f''(x)<0\) for all \(x\)
Solution: Answer will vary
26) \(f''(x)<0\) over \(−1<x<1,f''(x)>0,−3<x<−1,1<x<3,\) local maximum at \(x=0,\) local minima at \(x=±2\)
27) There is a local maximum at \(x=2,\) local minimum at \(x=1,\) and the graph is neither concave up nor concave down.
Solution: Answers will vary
28) There are local maxima at \(x=±1,\) the function is concave up for all \(x\), and the function remains positive for all \(x.\)
For the following exercises, determine
a. intervals where \(f\) is increasing or decreasing and
b. local minima and maxima of \(f\).
29) \(f(x)=sinx+sin^3x\) over −π<x<π
Solution:
a. Increasing over \(−\frac{π}{2}<x<\frac{π}{2},\) decreasing over \(x<−π\frac{π}{2},x>\frac{π}{2}\)
b. Local maximum at \(x=\frac{π}{2}\); local minimum at \(x=−\frac{π}{2}\)
28) \(f(x)=x^2+cosx\)
For the following exercises, determine a. intervals where \(f\) is concave up or concave down, and b. the inflection points of \(f\).
29) \(f(x)=x^3−4x^2+x+2\)
Solution:
a. Concave up for \(x>\frac{4}{3},\) concave down for \(x<\frac{34}{3}\)
b. Inflection point at \(x=\frac{4}{3}\)
For the following exercises, determine
a. intervals where \(f\) is increasing or decreasing,
b. local minima and maxima of \(f\),
c. intervals where \(f\) is concave up and concave down, and
d. the inflection points of \(f.\)
30) \(f(x)=x^2−6x\)
31) \(f(x)=x^3−6x^2\)
Solution: a. Increasing over \(x<0\) and \(x>4,\) decreasing over \(0<x<4\) b. Maximum at \(x=0\), minimum at \(x=4\) c. Concave up for \(x>2\), concave down for \(x<2\) d. Infection point at \(x=2\)
32) \(f(x)=x^4−6x^3\)
33) \(f(x)=x^{11}−6x^{10}\)
Solution: a. Increasing over \(x<0\) and \(x>\frac{60}{11}\), decreasing over \(0<x<\frac{60}{11}\) b. Minimum at \(x=\frac{60}{11}\) c. Concave down for \(x<\frac{54}{11}\), concave up for \(x>\frac{54}{11}\) d. Inflection point at \(x=\frac{54}{11}\)
34) \(f(x)=x+x^2−x^3\)
35) \(f(x)=x^2+x+1\)
Solution: a. Increasing over \(x>−\frac{1}{2}\), decreasing over \(x<−\frac{1}{2}\) b. Minimum at \(x=−\frac{1}{2}\) c. Concave up for all \(x\) d. No inflection points
36) \(f(x)=x^3+x^4\)
For the following exercises, determine
a. intervals where \(f\) is increasing or decreasing,
b. local minima and maxima of \(f,\)
c. intervals where \(f\) is concave up and concave down, and
d. the inflection points of \(f.\) Sketch the curve, then use a calculator to compare your answer. If you cannot determine the exact answer analytically, use a calculator.
37) [T] \(f(x)=sin(πx)−cos(πx)\) over \(x=[−1,1]\)
Solution: a. Increases over \(−\frac{1}{4}<x<\frac{3}{4},\) decreases over \(x>\frac{3}{4}\) and \(x<−\frac{1}{4}\) b. Minimum at \(x=−\frac{1}{4}\), maximum at \(x=\frac{3}{4}\) c. Concave up for \(−\frac{3}{4}<x<\frac{1}{4}\), concave down for \(x<−\frac{3}{4}\) and \(x>\frac{1}{4}\) d. Inflection points at \(x=−\frac{3}{4},x=\frac{1}{4}\)
38) [T] \(f(x)=x+sin(2x)\) over \(x=[−\frac{π}{2},\frac{π}{2}]\)
39) [T] \(f(x)=sinx+tanx\) over \((−\frac{π}{2},\frac{π}{2})\)
Solution: a. Increasing for all \(x\) b. No local minimum or maximum c. Concave up for \(x>0\), concave down for \(x<0\) d. Inflection point at \(x=0\)
40) [T] \(f(x)=(x−2)^2(x−4)^2\)
41) [T] \(f(x)=\frac{1}{1−x},x≠1\)
Solution: a. Increasing for all \(x\) where defined b. No local minima or maxima c. Concave up for \(x<1\); concave down for \(x>1\) d. No inflection points in domain
42) [T] \(f(x)=\frac{sinx}{x}\) over \(x=[−2π,2π] [2π,0)∪(0,2π]\)
43) \(f(x)=sin(x)e^x\) over \(x=[−π,π]\)
Solution: a. Increasing over \(−\frac{π}{4}<x<\frac{3π}{4}\), decreasing over \(x>\frac{3π}{4},x<−\frac{π}{4}\) b. Minimum at \(x=−\frac{π}{4}\), maximum at \(x=\frac{3π}{4}\) c. Concave up for \(−\frac{π}{2}<x<\frac{π}{2}\), concave down for \(x<−\frac{π}{2},x>\frac{π}{2}\) d. Infection points at \(x=±\frac{π}{2}\)
44) \(f(x)=lnx\sqrt{x},x>0\)
45) \(f(x)=\frac{1}{4}\sqrt{x}+\frac{1}{x},x>0\)
Solution: a. Increasing over \(x>4,\) decreasing over \(0<x<4\) b. Minimum at \(x=4\) c. Concave up for \(0<x<8\sqrt[3]{2}\), concave down for \(x>8\sqrt[3]{2}\) d. Inflection point at \(x=8\sqrt[3]{2}\)
46) \(f(x)=\frac{e^x}{x},x≠0\)
For the following exercises, interpret the sentences in terms of \(f,f′,\) and \(f''.\)
47) The population is growing more slowly. Here \(f\) is the population.
Solution: \(f>0,f′>0,f''<0\)
48) A bike accelerates faster, but a car goes faster. Here \(f=\) Bike’s position minus Car’s position.
49) The airplane lands smoothly. Here \(f\) is the plane’s altitude.
Solution: \(f>0,f′<0,f''<0\)
50) Stock prices are at their peak. Here \(f\)is the stock price.
51) The economy is picking up speed. Here \(f\) is a measure of the economy, such as GDP.
Solution: \(f>0,f′>0,f''>0\)
For the following exercises, consider a third-degree polynomial \(f(x),\) which has the properties f′(1)=0,f′(3)=0.
Determine whether the following statements are true or false. Justify your answer.
52) \(f(x)=0\) for some \(1≤x≤3\)
53) \(f''(x)=0\) for some \(1≤x≤3\)
Soltuion: True, by the Mean Value Theorem
54) There is no absolute maximum at \(x=3\)
55) If \(f(x)\) has three roots, then it has \(1\) inflection point.
Solution: True, examine derivative
56) If \(f(x)\) has one inflection point, then it has three real roots.
4.6: Limits at Infinity and Asymptotes
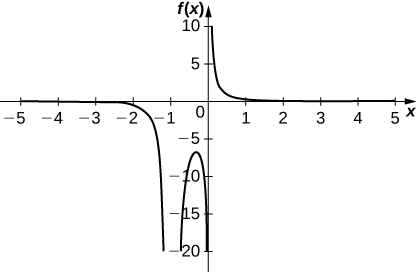
For the following exercises, examine the graphs. Identify where the vertical asymptotes are located.
1)
Solution: \(x=1\)
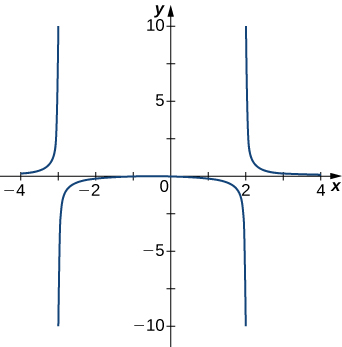
2)
3)
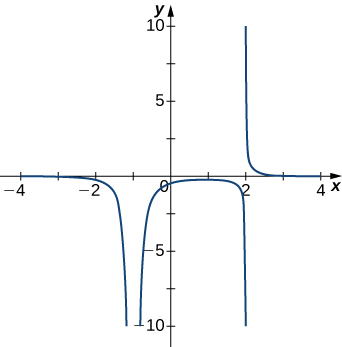
Solution: \(x=−1,x=2\)
4)
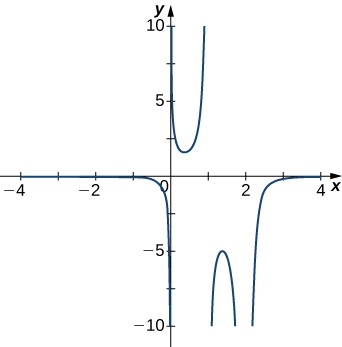
5)
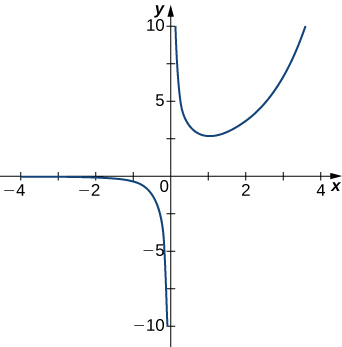
Solution: \(x=0\)
For the following functions \(f(x)\), determine whether there is an asymptote at \(x=a\). Justify your answer without graphing on a calculator.
6) \(f(x)=\frac{x+1}{x^2+5x+4},a=−1\)
7) \(f(x)=\frac{x}{x−2},a=2\)
Solution: Yes, there is a vertical asymptote
8) \(f(x)=(x+2)^{3/2},a=−2\)
9) \(f(x)=(x−1)^{−1/3},a=1\)
Solution: Yes, there is vertical asymptote
10) \(f(x)=1+x^{−2/5},a=1\)
For the following exercises, evaluate the limit.
11) \(lim_{x→∞}\frac{1}{3x+6}\)
Solution: \(0\)
12) \(lim_{x→∞}\frac{2x−5}{4x}\)
13) \(lim_{x→∞}\frac{x^2−2x+5}{x+2}\)
Solution: \(∞\)
14) \(lim_{x→−∞}\frac{3x^3−2x}{x^2+2x+8}\)
15) \(lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4}\)
Solution: \(−\frac{1}{7}\)
16) \(lim_{x→∞}\frac{3x}{\sqrt{x^2+1}}\)
17) \(lim_{x→−∞}\frac{\sqrt{4x2−1}}{x+2}\)
Solution: \(−2\)
18) \(lim_{x→∞}\frac{4x}{\sqrt{x2−1}}\)
19) \(lim_{x→−∞}\frac{4x}{\sqrt{x2−1}}\)
Solution: \(−4\)
20) \(lim_{x→∞}\frac{2\sqrt{x}}{x−\sqrt{x}+1}\)
For the following exercises, find the horizontal and vertical asymptotes.
21) \(f(x)=x−\frac{9}{x}\)
Solution: Horizontal: none, vertical: \(x=0\)
22) \(f(x)=\frac{1}{1−x^2}\)
23) \(f(x)=\frac{x^3}{4−x^2}\)
Solution: Horizontal: none, vertical: \(x=±2\)
24) \(f(x)=\frac{x^2+}{3x^2+1}\)
25) \(f(x)=sin(x)sin(2x)\)
Solution: Horizontal: none, vertical: none
26) \(f(x)=cosx+cos(3x)+cos(5x)\)
27) \(f(x)=\frac{xsin(x)}{x^2−1}\)
Solution: Horizontal: \(y=0,\) vertical: \(x=±1\)
28) \(f(x)=\frac{x}{sin(x)}\)
29) \(f(x)=(\frac{1}{x^3+x^2}\)
Solution: Horizontal: \(y=0,\) vertical: \(x=0\) and \(x=−1\)
30) \(f(x)=\frac{1}{x−1}−2x\)
31) \(f(x)=\frac{x^3+1}{x^3−1}\)
Solution: Horizontal: \(y=1,\) vertical: \(x=1\)
32) \(f(x)=\frac{sinx+cosx}{sinx−cosx}\)
33) \(f(x)=x−sinx\)
Solution: Horizontal: none, vertical: none
34) \(f(x)=\frac{1}{x}−\sqrt{x}\)
For the following exercises, construct a function \(f(x)\) that has the given asymptotes.
35) \(x=1\) and \(y=2\)
Solution: Answers will vary, for example: \(y=\frac{2x}{x−1}\)
36) \(x=1\) and \(y=0\)
37) \(y=4, x=−1\)
Solution: Answers will vary, for example: \(y=\frac{4x}{x+1}\)
38) \(x=0\)
For the following exercises, graph the function on a graphing calculator on the window \(x=[−5,5]\) and estimate the horizontal asymptote or limit. Then, calculate the actual horizontal asymptote or limit.
39) [T] \(f(x)=\frac{1}{x+10}\)
Solution: \(y=0\)
40) [T] \(f(x)=\frac{x+1}{x^2+7x+6}\)
41) [T] \(lim_{x→−∞}x^2+10x+25\)
Solution: \(∞\)
42) [T] \(lim_{x→−∞}\frac{x+2}{x^2+7x+6}\)
43) [T] \(lim_{x→∞}\frac(3x+2}{x+5}\)
Solution: \(y=3\)
For the following exercises, draw a graph of the functions without using a calculator. Be sure to notice all important features of the graph: local maxima and minima, inflection points, and asymptotic behavior.
44) \(y=3x^2+2x+4\)
45) \(y=x^3−3x^2+4\)
Solution:
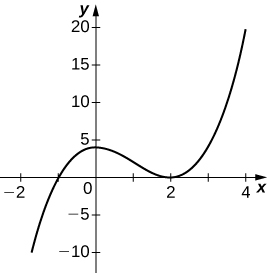
46) \(y=\frac{2x+1}{x^2+6x+5}\)
47) \(y=\frac{x^3+4x^2+3x}{3x+9}\)
Solution:
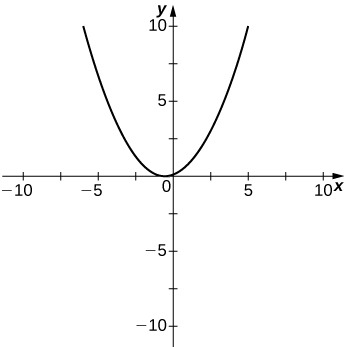
48) \(y=\frac{x^2+x−2}{x^2−3x−4}\)
49) \(y=\sqrt{x^2−5x+4}\)
Solution:
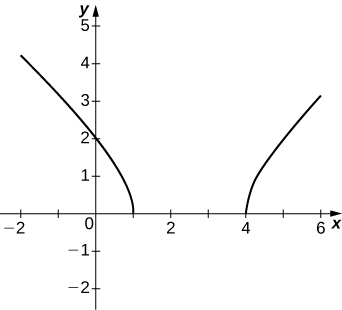
50) \(y=2x\sqrt{16−x^2}\)
51) \(y=\frac{cosx}{x}\), on \(x=[−2π,2π]\)
Solution:
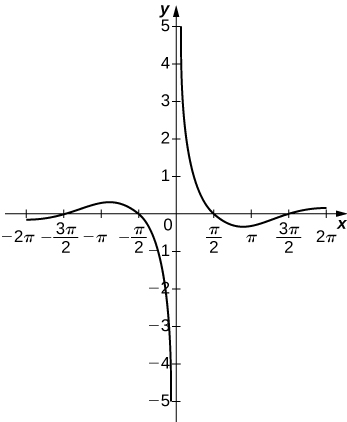
52) \(y=e^x−x^3\)\)
53) \(y=xtanx,x=[−π,π]\)
Solution:
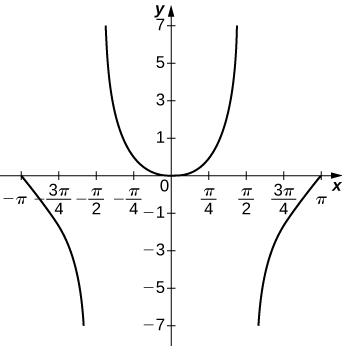
54) \(y=xln(x),x>0\)
55) \(y=x^2sin(x),x=[−2π,2π]\)
Solution:
56) For \(f(x)=\frac{P(x)}{Q(x)}\) to have an asymptote at \(y=2\) then the polynomials \(P(x)\) and \(Q(x)\) must have what relation?
57) For \(f(x)=\frac{P(x)}{Q(x)}\) to have an asymptote at \(x=0\), then the polynomials \(P(x)\) and \(Q(x).\) must have what relation?
Solution: \(Q(x).\) must have have \(x^{k+1}\) as a factor, where \(P(x)\) has \(x^k\) as a factor.
58) If \(f′(x)\) has asymptotes at \(y=3\) and \(x=1\), then \(f(x)\) has what asymptotes?
59) Both \(f(x)=\frac{1}{(x−1)}\) and \(g(x)=\frac{1}{(x−1)^2}\) have asymptotes at \(x=1\) and \(y=0.\) What is the most obvious difference between these two functions?
Solution: \(lim_{x→1^−f(x)andlimx→1−g(x)
True or false: Every ratio of polynomials has vertical asymptotes.
4.7: Applied Optimization Problems
For the following exercises, answer by proof, counterexample, or explanation.
1) When you find the maximum for an optimization problem, why do you need to check the sign of the derivative around the critical points?
Solution: The critical points can be the minima, maxima, or neither.
2) Why do you need to check the endpoints for optimization problems?
3) True or False. For every continuous nonlinear function, you can find the value \(x\) that maximizes the function.
Solution: False; \(y=−x^2\) has a minimum only
4) True or False. For every continuous nonconstant function on a closed, finite domain, there exists at least one \(x\) that minimizes or maximizes the function.
For the following exercises, set up and evaluate each optimization problem.
5) To carry a suitcase on an airplane, the length \(+width+\) height of the box must be less than or equal to \(62in\). Assuming the height is fixed, show that the maximum volume is \(V=h(31−(\frac{1}{2})h)^2.\) What height allows you to have the largest volume?
Solution: \(h=\frac{62}{3}\) in.
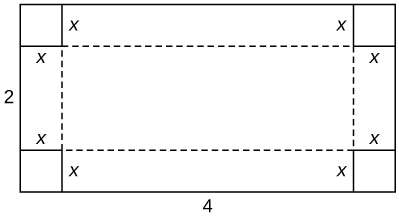
6) You are constructing a cardboard box with the dimensions \(2 m by 4 m.\) You then cut equal-size squares from each corner so you may fold the edges. What are the dimensions of the box with the largest volume?
7) Find the positive integer that minimizes the sum of the number and its reciprocal.
Solution: \(1\)
8) Find two positive integers such that their sum is \(10\), and minimize and maximize the sum of their squares.
For the following exercises, consider the construction of a pen to enclose an area.
9) You have \(400ft\) of fencing to construct a rectangular pen for cattle. What are the dimensions of the pen that maximize the area?
Solution: \(100ft by 100ft\)
10) You have \(800ft\) of fencing to make a pen for hogs. If you have a river on one side of your property, what is the dimension of the rectangular pen that maximizes the area?
11) You need to construct a fence around an area of \(1600ft.\) What are the dimensions of the rectangular pen to minimize the amount of material needed?
Solution: \(40ft by 40ft\)
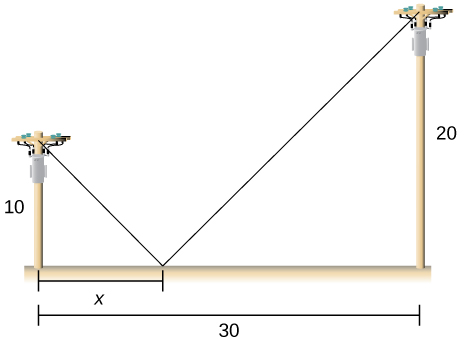
12) Two poles are connected by a wire that is also connected to the ground. The first pole is \(20ft\) tall and the second pole is \(10ft\) tall. There is a distance of \(30ft\) between the two poles. Where should the wire be anchored to the ground to minimize the amount of wire needed?
13) [T] You are moving into a new apartment and notice there is a corner where the hallway narrows from \(8 ft to 6 ft\). What is the length of the longest item that can be carried horizontally around the corner?
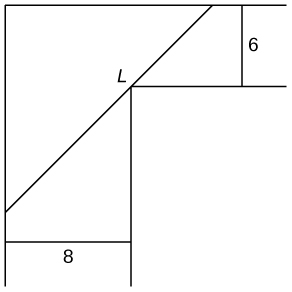
Solution: 19.73 ft
14) A patient’s pulse measures \(70 bpm, 80 bpm\), then \(120 bpm.\) To determine an accurate measurement of pulse, the doctor wants to know what value minimizes the expression \((x−70)^2+(x−80)^2+(x−120)^2\)? What value minimizes it?
15) In the previous problem, assume the patient was nervous during the third measurement, so we only weight that value half as much as the others. What is the value that minimizes \((x−70)^2+ (x−80)^2+\frac{1}{2}(x−120)^2?\)
Solution: \(84 bpm\)
16) You can run at a speed of \(6\) mph and swim at a speed of \(3\) mph and are located on the shore, \(4\) miles east of an island that is \(1\) mile north of the shoreline. How far should you run west to minimize the time needed to reach the island?
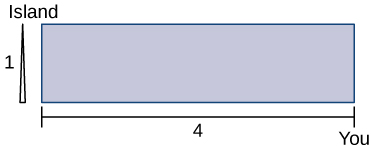
For the following problems, consider a lifeguard at a circular pool with diameter \(40m.\) He must reach someone who is drowning on the exact opposite side of the pool, at position \(C\). The lifeguard swims with a speed \(v\) and runs around the pool at speed \(w=3v.\)
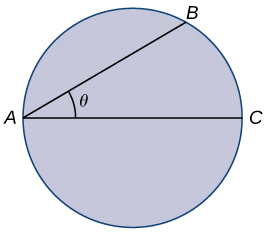
17) Find a function that measures the total amount of time it takes to reach the drowning person as a function of the swim angle, \(θ\).
Solution: \(T(θ)=\frac{40θ}{3v}+\frac{40cosθ}{v}\)
18) Find at what angle \(θ\) the lifeguard should swim to reach the drowning person in the least amount of time.
19) A truck uses gas as \(g(v)=av+\frac{b}{v}\), where \(v\) represents the speed of the truck and \(g\) represents the gallons of fuel per mile. At what speed is fuel consumption minimized?
Solution: \(v=\sqrt{\frac{b}{a}}\)
For the following exercises, consider a limousine that gets \(m(v)=\frac{(120−2v)}{5}mi/gal\) at speed \(v\), the chauffeur costs \($15/h\), and gas is \($3.5/gal.\)
20) Find the cost per mile at speed \(v.\)
21) Find the cheapest driving speed.
Solution: approximately \(34.02mph\)
For the following exercises, consider a pizzeria that sell pizzas for a revenue of \(R(x)=ax\) and costs \(C(x)=b+cx+dx^2\), where \(x\) represents the number of pizzas.
22) Find the profit function for the number of pizzas. How many pizzas gives the largest profit per pizza?
23) Assume that \(R(x)=10x\) and \(C(x)=2x+x^2\).How many pizzas sold maximizes the profit?
Solution: \(4\)
24) Assume that \(R(x)=15x,\) and \(C(x)=60+3x+\frac{1}{2}x^2\). How many pizzas sold maximizes the profit?
For the following exercises, consider a wire \(4ft\) long cut into two pieces. One piece forms a circle with radius r and the other forms a square of side \(x\).
25) Choose \(x\) to maximize the sum of their areas.
Solution: \(0\)
26) Choose \(x\) to minimize the sum of their areas.
For the following exercises, consider two nonnegative numbers \(x\) and \(y\) such that \(x+y=10\). Maximize and minimize the quantities.
27) \(xy\)
Solution: Maximal: \(x=5,y=5;\) minimal: \(x=0,y=10\) and \(y=0,x=10\)
28 \(x^2y^2\)
29) \(y−\frac{1}{x}\)
Solution: Maximal: \(x=1,y=9;\) minimal: none
30) \(x^2−y\)
For the following exercises, draw the given optimization problem and solve.
31) Find the volume of the largest right circular cylinder that fits in a sphere of radius \(1\).
Solution: \(\frac{4π}{3\sqrt{3}}\)
32) Find the volume of the largest right cone that fits in a sphere of radius \(1\).
33) Find the area of the largest rectangle that fits into the triangle with sides \(x=0,y=0\) and \(\frac{x}{4}+\frac{y}{6}=1.\)
Solution: \(6\)
34) Find the largest volume of a cylinder that fits into a cone that has base radius \(R\) and height \(h\).
35) Find the dimensions of the closed cylinder volume \(V=16π\) that has the least amount of surface area.
Solution: \(r=2,h=4\)
36) Find the dimensions of a right cone with surface area \(S=4π\) that has the largest volume.
For the following exercises, consider the points on the given graphs. Use a calculator to graph the functions.
37) [T] Where is the line \(y=5−2x\) closest to the origin?
Solution: \((2,1)\)
38) [T] Where is the line \(y=5−2x\) closest to point \((1,1)\)?
39) [T] Where is the parabola \(y=x^2\) closest to point \((2,0)\)?
Solution: \((0.8351,0.6974)\)
40) [T] Where is the parabola \(y=x^2\) closest to point \((0,3)\)?
For the following exercises, set up, but do not evaluate, each optimization problem.
41) A window is composed of a semicircle placed on top of a rectangle. If you have \(20ft\) of window-framing materials for the outer frame, what is the maximum size of the window you can create? Use r to represent the radius of the semicircle.

Solution: \(A=20r−2r^2−\frac{1}{2}πr^2\)
42) You have a garden row of \(20\) watermelon plants that produce an average of \(30\) watermelons apiece. For any additional watermelon plants planted, the output per watermelon plant drops by one watermelon. How many extra watermelon plants should you plant?
43) You are constructing a box for your cat to sleep in. The plush material for the square bottom of the box costs \($5/ft^2\) and the material for the sides costs \($2/ft^2\). You need a box with volume \(4ft^2\). Find the dimensions of the box that minimize cost. Use \(x\) to represent the length of the side of the box.
Solution: \(C(x)=5x^2+\frac{32}{x}\)
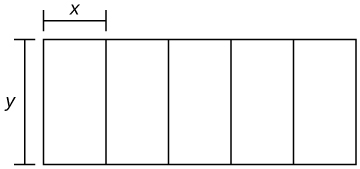
44) You are building five identical pens adjacent to each other with a total area of \(1000m^2\), as shown in the following figure. What dimensions should you use to minimize the amount of fencing?
Glossary
optimization problems
problems that are solved by finding the maximum or minimum value of a function
45) You are the manager of an apartment complex with \(50\) units. When you set rent at \($800/month,\) all apartments are rented. As you increase rent by \($25/month\), one fewer apartment is rented. Maintenance costs run \($50/month\) for each occupied unit. What is the rent that maximizes the total amount of profit?
Solution: \(P(x)=(50−x)(800+25x−50)\)
4.8: L’Hôpital’s Rule
For the following exercises, evaluate the limit.
1) Evaluate the limit \(lim_{x→∞}\frac{e^x}{x}\).
2) Evaluate the limit \(lim_{x→∞}\frac{e^x}{x^k}\).
Solution: \(∞\)
3) Evaluate the limit \(lim_{x→∞}\frac{lnx}{x^k}\).
4) Evaluate the limit \(lim_{x→a}\frac{x−a}{x^2−a^2}\).
Solution: \(\frac{1}{2a}\)
5. Evaluate the limit \(lim_{x→a}\frac{x−a}{x^3−a^3}\).
6. Evaluate the limit \(lim_{x→a}\frac{x−a}{x^n−a^n}\).
Solution: \(\frac{1}{na^{n−1}}\)
For the following exercises, determine whether you can apply L’Hôpital’s rule directly. Explain why or why not. Then, indicate if there is some way you can alter the limit so you can apply L’Hôpital’s rule.
7) \(lim_{x→0^+}x^2lnx\)
8) \(lim_{x→∞}x^{1/x}\)
Solution: Cannot apply directly; use logarithms
9) \(lim_{x→0}x^{2/x}\)
10) \(lim_{x→0}\frac{x^2}{1/x}\)
Solution: Cannot apply directly; rewrite as \(lim_{x→0}x^3\)
11) \(lim_{x→∞}\frac{e^x}{x}\)
For the following exercises, evaluate the limits with either L’Hôpital’s rule or previously learned methods.
21) \(lim_{x→3}\frac{x^2−9}{x−3}\)
Solution: \(6\)
22) \(lim_{x→3}\frac{x^2−9}{x+3}\)
23) \(lim_{x→0}\frac{(1+x)^{−2}−1}{x}\)
Solution: \(−2\)
24) \(lim_{x→π/2}\frac{cosx}{\frac{π}{2}−x}\)
25) \(lim_{x→π}\frac{x−π}{sinx}\)
Solution: \(−1\)
26) \(lim_{x→1}\frac{x−1}{sinx}\)
27) \(lim_{x→0}\frac{(1+x)^n−1}{x}\)
Solution: \(n\)
28) \(lim_{x→0}\frac{(1+x)^n−1−nx}{x^2}\)
29) \(lim_{x→0}\frac{sinx−tanx}{x^3}\)
Solution: \(−\frac{1}{2}\)
30) \(lim_{x→0}\frac{\sqrt{1+x}−\sqrt{1−x}}{x}\)
31) \(lim_{x→0}\frac{e^x−x−1}{x^2}\)
Solution: \(\frac{1}{2}\)
32) \(lim_{x→0}\frac{tanx}{\sqrt{x}}\)
33) \(lim_{x→1}\frac{x→1}{lnx}\)
Solution: \(1\)
34) \(lim_{x→0}(x+1)^{1/x}\)
35) \(lim_{x→1}\frac{\sqrt{x}−\sqrt[3]{x}}{x−1}\)
Solution: \(\frac{1}{6}\)
36) \(lim_{x→0^+}x^{2x}\)
37) \(lim_{x→∞}xsin(\frac{1}{x})\)
Solution: \(1\)
38) \(lim_{x→0}\frac{sinx−x}{x^2}\)
39) \(lim_{x→0^+}xln(x^4)\)
Solution: \(0\)
40) \(lim_{x→∞}(x−e^x)\)
41) \(lim_{x→∞}x^2e^{−x}\)
Solution: \(0\)
42) \(lim_{x→0}\frac{3^x−2^x}{x}\)
43) \(lim_{x→0}\frac{1+1/x}{1−1/x}\)
Solution: \(−1\)
44) \(lim_{x→π/4}(1−tanx)cotx\)
45) \(lim_{x→∞}xe^{1/}\)x
Solution: \(∞\)
46) \(lim_{x→0}x^{1/cosx}\)
47) \(lim_{x→0}x^{1/x}\)
Solution: \(1\)
48) \(lim_{x→0}(1−\frac{1}{x})^x\)
49) \(lim_{x→∞}(1−\frac{1}{x})^x\)
Solution: \(\frac{1}{e}\)
For the following exercises, use a calculator to graph the function and estimate the value of the limit, then use L’Hôpital’s rule to find the limit directly.
50) [T] \(lim_{x→0}\frac{e^x−1}{x}\)
51) [T] \(lim_{x→0}xsin(\frac{1}{x})\)
Solution: \(0\)
52) [T] \(lim_{x→1}\frac{x−1}{1−cos(πx)}\)
53) [T] \(lim_{x→1}\frac{e^{(x−1)}−1}{x−1}\)
Solution: \(1\)
54) [T] \(lim_{x→1}\frac{(x−1)^2}{lnx}\)
55) [T] \(lim_{x→π}\frac{1+cosx}{sinx}\)
Solution: \(0\)
56) [T] \(lim_{x→0}(cscx−\frac{1}{x})\)
57) [T] \(lim_{x→0^+}tan(x^x)\)
Solution: \(tan(1)\)
58) [T] \(lim_{x→0^+}\frac{lnx}{sinx}\)
59) [T] \(lim_{x→0}\frac{e^x−e^{−x}}{x}\)
Solution: \(2\)
4.9: Newton’s Method
For the following exercises, write Newton’s formula as \(x_{n+1}=F(x_n)\) for solving \(f(x)=0\).
1) \(f(x)=x^2+1\)
2) \(f(x)=x^3+2x+1\)
Solution: \(F(x_n)=x_n−\frac{x_n^3+2x_n+1}{3x_n^2+2}\)
3) \(f(x)=sinx\)
4) \(f(x)=e^x\)
Solution: \(F(x_n)=x_n−\frac{e^{x_n}}{e^{x_n}}\)
5) \(f(x)=x^3+3xe^x\)
For the following exercises, solve \(f(x)=0\) using the iteration \(x_{n+1}=x_{n−c}f(x_n)\), which differs slightly from Newton’s method. Find a c that works and a \(c\) that fails to converge, with the exception of \(c=0.\)
6) \(f(x)=x^2−4,\) with \(x_0=0\)
Solution: \(|c|>0.5\) fails, \(|c|≤0.5\) works
7) \(f(x)=x^2−4x+3,\) with \(x_0=2\)
8) What is the value of \(“c”\) for Newton’s method?
Solution: \(c=\frac{1}{f′(x_n)}\)
For the following exercises, start at
a. \(x_0=0.6\) and
b. \(x_0=2.\)
Compute \(x_1\) and \(x_2\) using the specified iterative method.
9) \(x_{n+1}=x_n^2−\frac{1}{2}\)
10) \(x_{n+1}=2x_n(1−x_n)\)
Solution: \(a. x_1=\frac{12}{25},x_2=\frac{312}{625}; b. x_1=−4, x_2=−40\)
11) \(x_{n+1}=\sqrt{x_n}\)
12) \(x_{n+1}=\frac{1}{\sqrt{x_n}}\)
Solution: \(a. x_1=1.291, x_2=0.8801; b. x_1=0.7071, x_2=1.189\)
13) \(x_{n+1}=3x_n(1−x_n)\)
14) \(x_{n+1}=x_n^2+x_{n−2}\)
Solution: \(a. x_1=−\frac{26}{25}, x_2=−\frac{1224}{625}; b. x_1=4,x_2=18\)
15) \(x_{n+1}=\frac{1}{2}x_n−1\)
16) \(x_{n+1}=|x_n|\)
Solution: \(a. x_1=\frac{6}{10},x_2=\frac{6}{10}; b. x_1=2,x_2=2\)
For the following exercises, solve to four decimal places using Newton’s method and a computer or calculator. Choose any initial guess \(x_0\) that is not the exact root.
17) \(x^2−10=0\)
18) \(x^4−100=0\)
Solution: \(3.1623or−3.1623\)
19) \(x^2−x=0\)
20) \(x^3−x=0\)
Solution: \(0,−1 or 1\)
21) \(x+5cos(x)=0\)
22) \(x+tan(x)=0,\) choose \(x_0∈(−\frac{π}{2},\frac{π}{2})\)
Solution: \(0\)
23) \(\frac{1}{1−x}=2\)
24) \(1+x+x^2+x^3+x^4=2\)
Solution: \(0.5188\) or \(−1.2906\)
25) \(x^3+(x+1)^3=10^3\)
26) \(x=sin2^(x)\)
Solution: \(0\)
For the following exercises, use Newton’s method to find the fixed points of the function where \(f(x)=x\); round to three decimals.
27) \(sinx\)
28) \(tan(x)\) on \(x=(\frac{π}{2},\frac{3π}{2})\)
Solution: \(4.493\)
29) \(e^x−2\)
30) \(ln(x)+2\)
Solution: \(0.159,3.146\)
31) Newton’s method can be used to find maxima and minima of functions in addition to the roots. In this case apply Newton’s method to the derivative function \(f′(x)\) to find its roots, instead of the original function. For the following exercises, consider the formulation of the method.
To find candidates for maxima and minima, we need to find the critical points \(f′(x)=0.\) Show that to solve for the critical points of a function \(f(x)\), Newton’s method is given by \(x_{n+1}=x_n−\frac{f′(x_n)}{f''(x_n)}\).
What additional restrictions are necessary on the function \(f\)?
Solution: We need \(f\) to be twice continuously differentiable.
For the following exercises, use Newton’s method to find the location of the local minima and/or maxima of the following functions; round to three decimals.
32) Minimum of \(f(x)=x^2+2x+4\)
33) Minimum of \(f(x)=3x^3+2x^2−16\)
Solution: \(x=0\)
34) Minimum of \(f(x)=x^2e^x\)
35) Maximum of \(f(x)=x+\frac{1}{x}\)
Solution: \(x=−1\)
36) Maximum of \(f(x)=x^3+10x^2+15x−2\)
37) Maximum of \(f(x)=\frac{\sqrt{x}−\sqrt[3]{x}}{x}\)
Solution: \(x=5.619\)
38) Minimum of \(f(x)=x^2sinx,\) closest non-zero minimum to \(x=0\)
39) Minimum of \(f(x)=x^4+x^3+3x^2+12x+6\)
Solution: \(x=−1.326\)
For the following exercises, use the specified method to solve the equation. If it does not work, explain why it does not work.
40) Newton’s method, \(x^2+2=0\)
41) Newton’s method, \(0=e^x\)
Solution: There is no solution to the equation.
42) Newton’s method, \(0=1+x^2\) starting at \(x_0=0\)
43) Solving \(x_{n+1}=−x_n^3\) starting at \(x_0=−1\)
Solution: It enters a cycle.
For the following exercises, use the secant method, an alternative iterative method to Newton’s method. The formula is given by
\(x_n=x_{n−1}−f(x_{n−1})\frac{x_{n−1}−x_{n−2}}{f(x_{n−1})−f(x_{n−2})}.\)
44) a root to \(0=x^2−x−3\) accurate to three decimal places.
45) Find a root to \(0=sinx+3x\) accurate to four decimal places.
Solution: \(0\)
46) Find a root to \(0=e^x−2\) accurate to four decimal places.
47) Find a root to \(ln(x+2)=\frac{1}{2}\) accurate to four decimal places.
Solution: \(−0.3513\)
48) Why would you use the secant method over Newton’s method? What are the necessary restrictions on \(f\)?
For the following exercises, use both Newton’s method and the secant method to calculate a root for the following equations. Use a calculator or computer to calculate how many iterations of each are needed to reach within three decimal places of the exact answer. For the secant method, use the first guess from Newton’s method.
49) \(f(x)=x^2+2x+1,x_0=1\)
Solution: Newton: \(11\) iterations, secant: \(16\) iterations
50) \(f(x)=x^2,x_0=1\)
51) \(f(x)=sinx,x_0=1\)
Solution: Newton: three iterations, secant: six iterations
52) \(f(x)=e^x−1,x_0=2\)
53) \(f(x)=x^3+2x+4,x_0=0\)
Solution: Newton: five iterations, secant: eight iterations
In the following exercises, consider Kepler’s equation regarding planetary orbits, \(M=E−εsin(E)\), where \(M\) is the mean anomaly, \(E\) is eccentric anomaly, and ε measures eccentricity.
54) Use Newton’s method to solve for the eccentric anomaly \(E\) when the mean anomaly \(M=\frac{π}{3}\) and the eccentricity of the orbit \(ε=0.25;\) round to three decimals.
55) Use Newton’s method to solve for the eccentric anomaly \(E\) when the mean anomaly \(M=\frac{3π}{2}\) and the eccentricity of the orbit \(ε=0.8;\) round to three decimals.
Solution: \(E=4.071\)
The following two exercises consider a bank investment. The initial investment is \($10,000\). After \(25\) years, the investment has tripled to \($30,000.\)
56) Use Newton’s method to determine the interest rate if the interest was compounded annually.
57) Use Newton’s method to determine the interest rate if the interest was compounded continuously.
Solution: \(4.394%\)
58) The cost for printing a book can be given by the equation \(C(x)=1000+12x+(\frac{1}{2})x^{2/3}\). Use Newton’s method to find the break-even point if the printer sells each book for \($20.\)
4.10: Antiderivatives
For the following exercises, show that \(F(x)\) are antiderivatives of \(f(x)\).
1) \(F(x)=5x^3+2x^2+3x+1,f(x)=15x^2+4x+3\)
Solution: \(F′(x)=15x^2+4x+3\)
2) \(F(x)=x^2+4x+1,f(x)=2x+4\)
3) \(F(x)=x^2e^x,f(x)=e^x(x^2+2x)\)
Solution: \(F′(x)=2xe^x+x^2e^x\)
4) \(F(x)=cosx,f(x)=−sinx\)
5) \(F(x)=e^x,f(x)=e^x\)
Solution: \(F′(x)=e^x\)
For the following exercises, find the antiderivative of the function.
6) \(f(x)=\frac{1}{x^2}+x\)
7) \(f(x)=e^x−3x^2+sinx\)
Solution: \(F(x)=e^x−x^3−cos(x)+C\)
8) \(f(x)=e^x+3x−x^2\)
9) \(f(x)=x−1+4sin(2x)\)
Solution: \(F(x)=\frac{x^2}{2}−x−2cos(2x)+C\)
For the following exercises, find the antiderivative \(F(x)\) of each function \(f(x).\)
10) \(f(x)=5x^4+4x^5\)
11) \(f(x)=x+12x^2\)
Solution: \(F(x)=\frac{1}{2}x^2+4x^3+C\)
12) \(f(x)=\frac{1}{\sqrt{x}}\)
13) \(f(x)=(\sqrt{x})^3\)
Solution: \(F(x)=\frac{2}{5}(\sqrt{x})^5+C\)
14) \(f(x)=x^{1/3}+(2x)^{1/3}\)
15) \(f(x)=\frac{x^{1/3}}{x^{2/3}}\)
Solution: \((F(x)=\frac{3}{2}x^{2/3}+C\)
16) \(f(x)=2sin(x)+sin(2x)\)
17) \(f(x)=sec^2(x)+1\)
Solution: (F(x)=x+tan(x)+C\)
18) \(f(x)=sinxcosx\)
19) \(f(x)=sin^2(x)cos(x)\)
Solution: \(F(x)=\frac{1}{3}sin^3(x)+C\)
20) \(f(x)=0\)
21) \(f(x)=\frac{1}{2}csc^2(x)+\frac{1}{x^2}\)
Solution: \(F(x)=−\frac{1}{2}cot(x)−\frac{1}{x}+C\)
22) \(f(x)=cscxcotx+3x\)
23) \(f(x)=4cscxcotx−secxtanx\)
Solution: \(F(x)=−secx−4cscx+C\)
24) \(f(x)=8secx(secx−4tanx)\)
25) \(f(x)=\frac{1}{2}e^{−4x}+sinx\)
Solution: \(F(x)=−\frac{1}{8}e^{−4x}−cosx+C\)
For the following exercises, evaluate the integral.
26) \(∫(−1)dx\)
27) \(∫sinxdx\)
Solution: \(−cosx+C\)
28) \(∫(4x+\sqrt{x})dx\)
29) \(∫\frac{3x^2+2}{x^2}dx\)
Solution: \(3x−\frac{2}{x}+C\)
30) \(∫(secxtanx+4x)dx\)
31) \(∫(4\sqrt{x}+\sqrt[4]{x})dx\)
Solution: \(\frac{8}{3}x^{3/2}+\frac{4}{5}x^{5/4}+C\)
32) \(∫(x^{−1/3}−x^{2/3})dx\)
33) \(∫\frac{14x^3+2x+1}{x^3}dx\)
Solution: \(14x−\frac{2}{x}−\frac{1}{2x^2}+C\)
34) \(∫(e^x+e^{−x})dx\)
For the following exercises, solve the initial value problem.
35) \(f′(x)=x^{−3},f(1)=1\)
Solution: \(f(x)=−\frac{1}{2x^2}+\frac{3}{2}\)
36) \(f′(x)=\sqrt{x}+x^2,f(0)=2\)
37) \(f′(x)=cosx+sec^2(x),f(\frac{π}{4})=2+\frac{\sqrt{2}}{2}\)
Solution: \(f(x)=sinx+tanx+1\)
38) \(f′(x)=x^3−8x^2+16x+1,f(0)=0\)
39 )\(f′(x)=\frac{2}{x^2}−\frac{x^2}{2},f(1)=0\)
Solution: \(f(x)=−\frac{1}{6}x^3−\frac{2}{x}+\frac{13}{6}\)
For the following exercises, find two possible functions \(f\) given the second- or third-order derivatives
40) \(f''(x)=x^2+2\)
41) \(f''(x)=e^{−x}\)
Solution: Answers may vary; one possible answer is \(f(x)=e^{−x}\)
42) \(f''(x)=1+x\)
43) \(f'''(x)=cosx\)
Solution: Answers may vary; one possible answer is \(f(x)=−sinx\)
44) \(f'''(x)=8e^{−2x}−sinx\)
45) A car is being driven at a rate of \(40\) mph when the brakes are applied. The car decelerates at a constant rate of \(10\) ft/sec2. How long before the car stops?
Solution: \(5.867\) sec
46) In the preceding problem, calculate how far the car travels in the time it takes to stop.
47) You are merging onto the freeway, accelerating at a constant rate of \(12\) ft/sec2. How long does it take you to reach merging speed at \(60\) mph?
Solution: \(7.333\) sec
48) Based on the previous problem, how far does the car travel to reach merging speed?
49) A car company wants to ensure its newest model can stop in \(8\) sec when traveling at \(75\) mph. If we assume constant deceleration, find the value of deceleration that accomplishes this.
Solution: \(13.75 ft/sec^2\)
50) A car company wants to ensure its newest model can stop in less than \(450\) ft when traveling at \(60\) mph. If we assume constant deceleration, find the value of deceleration that accomplishes this.
For the following exercises, find the antiderivative of the function, assuming \(F(0)=0.\)
51) [T] \(f(x)=x^2+2\)
Solution: \(F(x)=\frac{1}{3}x^3+2x\)
52) [T] \(f(x)=4x−\sqrt{x}\)
53) [T] \(f(x)=sinx+2x\)
Solution: \(F(x)=x^2−cosx+1\)
54) \([T] f(x)=e^x\)
55) \([T] f(x)=\frac{1}{(x+1)^2}\)
Solution: \(F(x)=−\frac{1}{(x+1)}+1\)
56) [T] \(f(x)=e^{−2x}+3x^2\)
For the following exercises, determine whether the statement is true or false. Either prove it is true or find a counterexample if it is false.
57) If \(f(x)\) is the antiderivative of \(v(x)\), then \(2f(x)\) is the antiderivative of \(2v(x).\)
Solution: True
58) If \(f(x)\) is the antiderivative of \(v(x)\), then \(f(2x)\) is the antiderivative of \(v(2x).\)
59) If \(f(x)\) is the antiderivative of \(v(x),\) then \(f(x)+1\) is the antiderivative of \(v(x)+1.\)
Solution: False
60) If \(f(x)\) is the antiderivative of \(v(x)\), then \((f(x))^2\) is the antiderivative of \((v(x))^2.\)
Chapter Review Exercises
True or False? Justify your answer with a proof or a counterexample. Assume that \(f(x)\) is continuous and differentiable unless stated otherwise.
1) If \(f(−1)=−6\) and \(f(1)=2\), then there exists at least one point \(x∈[−1,1]\) such that \(f′(x)=4.\)
Solution: True, by Mean Value Theorem
2) If \(f′(c)=0,\) there is a maximum or minimum at \(x=c.\)
3) There is a function such that \(f(x)<0,f′(x)>0,\) and \(f''(x)<0.\) (A graphical “proof” is acceptable for this answer.)
Solution: True
4) There is a function such that there is both an inflection point and a critical point for some value \(x=a.\)
5) Given the graph of \(f′\), determine where \(f\) is increasing or decreasing.
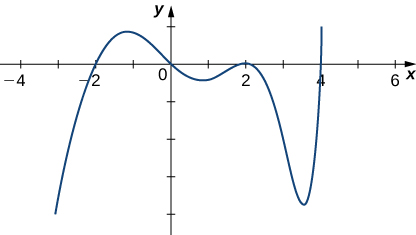
Solution: Increasing: \((−2,0)∪(4,∞)\), decreasing: \((−∞,−2)∪(0,4)\)
6) The graph of \(f\) is given below. Draw \(f′\).
7) Find the linear approximation \(L(x)\) to \(y=x^2+tan(πx)\) near \(x=\frac{1}{4}.\)
Solution: \(L(x)=\frac{17}{16}+\frac{1}{2}(1+4π)(x−\frac{1}{4})\)
8) Find the differential of \(y=x^2−5x−6\) and evaluate for \(x=2\) with \(dx=0.1.\)
Find the critical points and the local and absolute extrema of the following functions on the given interval.
9) \(f(x)=x+sin^2(x)\) over \([0,π]\)
Solution: Critical point: \(x=\frac{3π}{4},\) absolute minimum: \(x=0,\) absolute maximum: \(x=π\)
10) \(f(x)=3x^4−4x^3−12x^2+6\) over \([−3,3]\)
Determine over which intervals the following functions are increasing, decreasing, concave up, and concave down.
11) \(x(t)=3t^4−8t^3−18t^2\)
Solution: Increasing: \((−1,0)∪(3,∞),\) decreasing: \((−∞,−1)∪(0,3),\) concave up: \((−∞,\frac{1}{3}(2−\sqrt{13}))∪(\frac{1}{3}(2+\sqrt{13}),∞)\), concave down: \((\frac{1}{3}(2−\sqrt{13}),\frac{1}{3}(2+\sqrt{13}))\)
12) \(y=x+sin(πx)\)
13) \(g(x)=x−\sqrt{x}\)
Solution: Increasing: \((\frac{1}{4},∞),\) decreasing: \((0,\frac{1}{4})\), concave up: \((0,∞),\) concave down: nowhere
14) \(f(θ)=sin(3θ)\)
Evaluate the following limits.
15) \(lim_{x→∞}\frac{3x\sqrt{x^2+1}}{\sqrt{x4−1}}\)
Solution: \(3\)
16) \(lim_{x→∞}cos(\frac{1}{x})\)
17) \(lim_{x→1}\frac{x−1}{sin(πx)}\)
Solution: \(−\frac{1}{π}\)
18) \(lim_{x→∞}(3x)^{1/x}\)
Use Newton’s method to find the first two iterations, given the starting point.
19) \(y=x^3+1,x_0=0.5\)
Solution: \(x_1=−1,x_2=−1\)
20) \(\frac{1}{x+1}=\frac{1}{2},x_0=0\)
Find the antiderivatives \(F(x)\) of the following functions.
21) \(g(x)=\sqrt{x}−\frac{1}{x^2}\)
Solution: ](F(x)=\frac{2x^{3/2}}{3}+\frac{1}{x}+C\)
22) \(f(x)=2x+6cosx,F(π)=π^2+2\)
Graph the following functions by hand. Make sure to label the inflection points, critical points, zeros, and asymptotes.
23) \(y=\frac{1}{x(x+1)^2}\)
Solution:
Inflection points: none; critical points: \(x=−\frac{1}{3}\); zeros: none; vertical asymptotes: \(x=−1, x=0\); horizontal asymptote: \(y=0\)
24) \(y=x−\sqrt{4−x^2}\)
25) A car is being compacted into a rectangular solid. The volume is decreasing at a rate of \(2 m^3/sec\). The length and width of the compactor are square, but the height is not the same length as the length and width. If the length and width walls move toward each other at a rate of \(0.25\) m/sec, find the rate at which the height is changing when the length and width are \(2\) m and the height is \(1.5\) m.
Solution: The height is decreasing at a rate of \(0.125\) m/sec
26) A rocket is launched into space; its kinetic energy is given by \(K(t)=(\frac{1}{2})m(t)v(t)^2\), where \(K\) is the kinetic energy in joules, \(m\) is the mass of the rocket in kilograms, and \(v\) is the velocity of the rocket in meters/second. Assume the velocity is increasing at a rate of \(15 m/sec^2\) and the mass is decreasing at a rate of \(10\) kg/sec because the fuel is being burned. At what rate is the rocket’s kinetic energy changing when the mass is \(2000\) kg and the velocity is \(5000\) m/sec? Give your answer in mega-Joules (MJ), which is equivalent to \(10^6\) J.
27) The famous Regiomontanus’ problem for angle maximization was proposed during the \(15\) th century. A painting hangs on a wall with the bottom of the painting a distance \(a\) feet above eye level, and the top \(b\) feet above eye level. What distance x (in feet) from the wall should the viewer stand to maximize the angle subtended by the painting, \(θ\)?
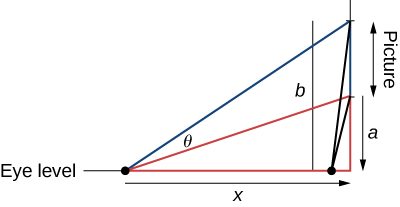
Solution: \(x=\sqrt{ab}\) feet
28) An airline sells tickets from Tokyo to Detroit for \($1200.\) There are \(500\) seats available and a typical flight books \(350\) seats. For every \($10\) decrease in price, the airline observes an additional five seats sold. What should the fare be to maximize profit? How many passengers would be onboard?

