4.E: Open Stax 4.1 - 4.5 Exercises
- Page ID
- 13642
These are homework exercises to accompany OpenStax's "Calculus" Textmap.
4.1: Related Rates
For the following exercises, find the quantities for the given equation.
1) Find \(\frac{dy}{dt}\) at \(x=1\) and \(y=x^2+3\) if \(\frac{dx}{dt}=4.\)
Solution: \(8\)
2) Find \(\frac{dx}{dt}\) at \(x=−2\) and \(y=2x^2+1\) if \(\frac{dy}{dt}=−1.\)
3) Find \(\frac{dz}{dt}\) at \((x,y)=(1,3)\) and \(z^2=x^2+y^2\) if \(\frac{dx}{dt}=4\) and \(\frac{dy}{dt}=3\).
Solution: \(\frac{13}{\sqrt{10}}\)
For the following exercises, sketch the situation if necessary and used related rates to solve for the quantities.
4) [T] If two electrical resistors are connected in parallel, the total resistance (measured in ohms, denoted by the Greek capital letter omega, \(Ω\)) is given by the equation \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}.\) If \(R_1\) is increasing at a rate of \(0.5Ω/min\) and \(R_2\) decreases at a rate of \(1.1Ω/min\), at what rate does the total resistance change when \(R_1=20Ω\) and \(R_2=50Ω/min\)?
5) A 10-ft ladder is leaning against a wall. If the top of the ladder slides down the wall at a rate of 2 ft/sec, how fast is the bottom moving along the ground when the bottom of the ladder is 5 ft from the wall?
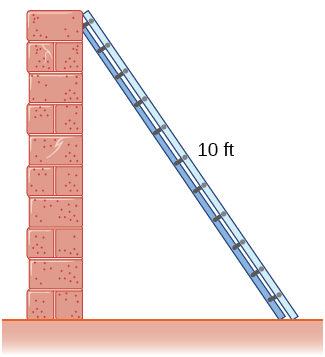
Solution: \(2\sqrt{3} ft/sec\)
6) A 25-ft ladder is leaning against a wall. If we push the ladder toward the wall at a rate of 1 ft/sec, and the bottom of the ladder is initially \(20ft\) away from the wall, how fast does the ladder move up the wall \(5sec\) after we start pushing?
7) Two airplanes are flying in the air at the same height: airplane A is flying east at 250 mi/h and airplane B is flying north at \(300mi/h.\) If they are both heading to the same airport, located 30 miles east of airplane A and 40 miles north of airplane B, at what rate is the distance between the airplanes changing?
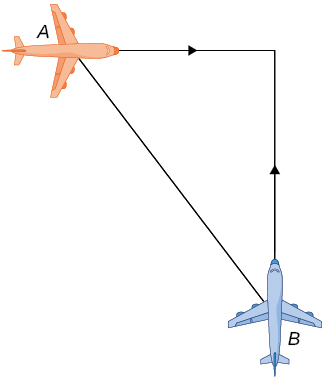
Solution: The distance is decreasing at \(390mi/h.\)
8) You and a friend are riding your bikes to a restaurant that you think is east; your friend thinks the restaurant is north. You both leave from the same point, with you riding at 16 mph east and your friend riding \(12mph\) north. After you traveled \(4mi,\) at what rate is the distance between you changing?
9) Two buses are driving along parallel freeways that are \(5mi\) apart, one heading east and the other heading west. Assuming that each bus drives a constant \(55mph\), find the rate at which the distance between the buses is changing when they are \(13mi\) part, heading toward each other.
Solution: The distance between them shrinks at a rate of \(\frac{1320}{13}≈101.5mph.\)
10) A 6-ft-tall person walks away from a 10-ft lamppost at a constant rate of \(3ft/sec.\) What is the rate that the tip of the shadow moves away from the pole when the person is 10ft away from the pole?
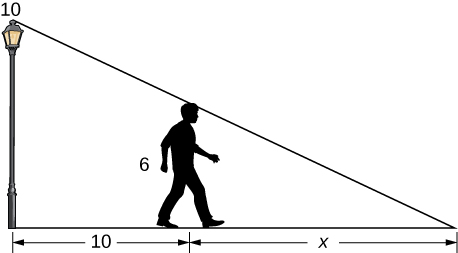
Using the previous problem, what is the rate at which the tip of the shadow moves away from the person when the person is 10 ft from the pole?
Solution: \(\frac{9}{2} ft/sec\)
11) A 5-ft-tall person walks toward a wall at a rate of 2 ft/sec. A spotlight is located on the ground 40 ft from the wall. How fast does the height of the person’s shadow on the wall change when the person is 10 ft from the wall?
12) Using the previous problem, what is the rate at which the shadow changes when the person is 10 ft from the wall, if the person is walking away from the wall at a rate of 2 ft/sec?
Solution: It grows at a rate \(\frac{4}{9}\) ft/sec
13) A helicopter starting on the ground is rising directly into the air at a rate of 25 ft/sec. You are running on the ground starting directly under the helicopter at a rate of 10 ft/sec. Find the rate of change of the distance between the helicopter and yourself after 5 sec.
Solution: The distance is increasing at \((\frac{135\sqrt{26})}{26}\) ft/sec
14) For the following exercises, draw and label diagrams to help solve the related-rates problems.
The side of a cube increases at a rate of \(\frac{1}{2}\) m/sec. Find the rate at which the volume of the cube increases when the side of the cube is 4 m.
The volume of a cube decreases at a rate of \(10\) m/sec. Find the rate at which the side of the cube changes when the side of the cube is 2 m.
Slution: \(−\frac{5}{6}\) m/sec
15) The radius of a circle increases at a rate of \(2\) m/sec. Find the rate at which the area of the circle increases when the radius is 5 m.
16) The radius of a sphere decreases at a rate of \(3\) m/sec. Find the rate at which the surface area decreases when the radius is 10 m.
Solution: \(240π m^2/sec\)
17) The radius of a sphere increases at a rate of 1 m/sec. Find the rate at which the volume increases when the radius is \(20\) m.
18) The radius of a sphere is increasing at a rate of 9 cm/sec. Find the radius of the sphere when the volume and the radius of the sphere are increasing at the same numerical rate.
Solution: \(\frac{1}{2\sqrt{π}}\) cm
19) The base of a triangle is shrinking at a rate of 1 cm/min and the height of the triangle is increasing at a rate of 5 cm/min. Find the rate at which the area of the triangle changes when the height is 22 cm and the base is 10 cm.
20) A triangle has two constant sides of length 3 ft and 5 ft. The angle between these two sides is increasing at a rate of 0.1 rad/sec. Find the rate at which the area of the triangle is changing when the angle between the two sides is \(π/6.\)
Solution: The area is increasing at a rate \(\frac{(3\sqrt{3})}{8}ft_2/sec.\)
21) A triangle has a height that is increasing at a rate of 2 cm/sec and its area is increasing at a rate of 4 \(cm^2/sec\). Find the rate at which the base of the triangle is changing when the height of the triangle is 4 cm and the area is 20 \(cm^2\).
For the following exercises, consider a right cone that is leaking water. The dimensions of the conical tank are a height of 16 ft and a radius of 5 ft.
22) How fast does the depth of the water change when the water is 10 ft high if the cone leaks water at a rate of 10 \(ft^3/min\)?
Solution: The depth of the water decreases at \(\frac{128}{125π}\) ft/min.
23) Find the rate at which the surface area of the water changes when the water is 10 ft high if the cone leaks water at a rate of 10 \(ft^3/min\).
24) If the water level is decreasing at a rate of 3 in./min when the depth of the water is 8 ft, determine the rate at which water is leaking out of the cone.
Solution: The volume is decreasing at a rate of \(\frac{(25π)}{16}ft^3/min.\)
25) A vertical cylinder is leaking water at a rate of 1 \(ft^3/sec\). If the cylinder has a height of 10 ft and a radius of 1 ft, at what rate is the height of the water changing when the height is 6 ft?
26) A cylinder is leaking water but you are unable to determine at what rate. The cylinder has a height of 2 m and a radius of 2 m. Find the rate at which the water is leaking out of the cylinder if the rate at which the height is decreasing is 10 cm/min when the height is 1 m.
Solution: The water flows out at rate \(\frac{(2π)}{5}m_3/min.\)
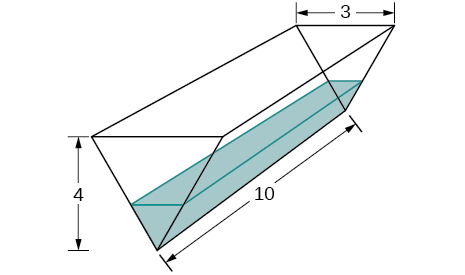
27) A trough has ends shaped like isosceles triangles, with width 3 m and height 4 m, and the trough is 10 m long. Water is being pumped into the trough at a rate of \(5m^3/min\). At what rate does the height of the water change when the water is 1 m deep?
28) A tank is shaped like an upside-down square pyramid, with base of 4 m by 4 m and a height of 12 m (see the following figure). How fast does the height increase when the water is 2 m deep if water is being pumped in at a rate of \(\frac{2}{3}\) m/sec?
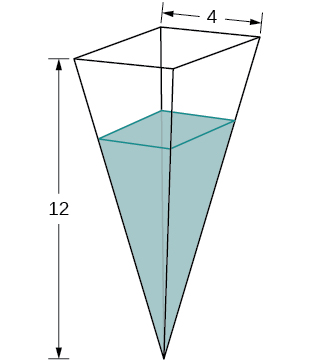
Solution: \(\frac{3}{2} m/sec\)
For the following problems, consider a pool shaped like the bottom half of a sphere, that is being filled at a rate of 25 \(ft^3\)/min. The radius of the pool is 10 ft.
29) Find the rate at which the depth of the water is changing when the water has a depth of 5 ft.
30) Find the rate at which the depth of the water is changing when the water has a depth of 1 ft.
Solution: \(\frac{25}{19π} ft/min\)
31) If the height is increasing at a rate of 1 in./sec when the depth of the water is 2 ft, find the rate at which water is being pumped in.
32) Gravel is being unloaded from a truck and falls into a pile shaped like a cone at a rate of 10 \(ft^3/min\). The radius of the cone base is three times the height of the cone. Find the rate at which the height of the gravel changes when the pile has a height of 5 ft.
Solution: \(\frac{2}{45π} ft/min\)
33) Using a similar setup from the preceding problem, find the rate at which the gravel is being unloaded if the pile is 5 ft high and the height is increasing at a rate of 4 in./min.
For the following exercises, draw the situations and solve the related-rate problems.
34) You are stationary on the ground and are watching a bird fly horizontally at a rate of \(10\) m/sec. The bird is located 40 m above your head. How fast does the angle of elevation change when the horizontal distance between you and the bird is 9 m?
Solution: The angle decreases at \(\frac{400}{1681}rad/sec.\)
35) You stand 40 ft from a bottle rocket on the ground and watch as it takes off vertically into the air at a rate of 20 ft/sec. Find the rate at which the angle of elevation changes when the rocket is 30 ft in the air.
36) A lighthouse, L, is on an island 4 mi away from the closest point, P, on the beach (see the following image). If the lighthouse light rotates clockwise at a constant rate of 10 revolutions/min, how fast does the beam of light move across the beach 2 mi away from the closest point on the beach?
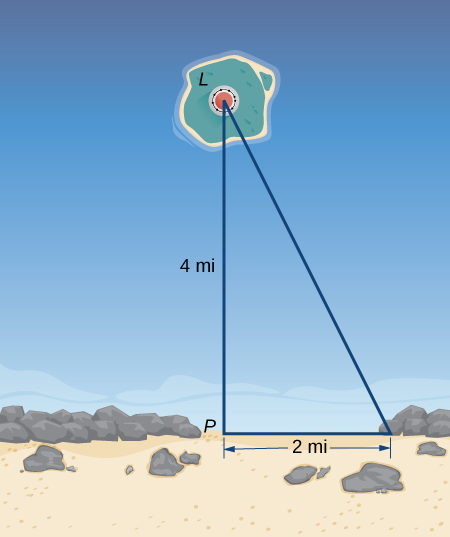
Solution: \(100π/min\)
37)Using the same setup as the previous problem, determine at what rate the beam of light moves across the beach 1 mi away from the closest point on the beach.
38) You are walking to a bus stop at a right-angle corner. You move north at a rate of 2 m/sec and are 20 m south of the intersection. The bus travels west at a rate of 10 m/sec away from the intersection – you have missed the bus! What is the rate at which the angle between you and the bus is changing when you are 20 m south of the intersection and the bus is 10 m west of the intersection?
Solution: The angle is changing at a rate of \(\frac{21}{25}rad/sec\).
For the following exercises, refer to the figure of baseball diamond, which has sides of 90 ft.
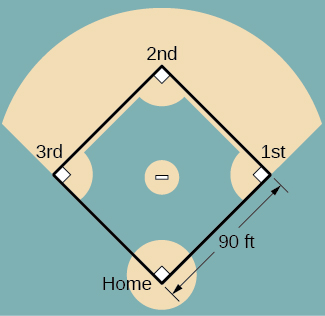
39) [T] A batter hits a ball toward third base at 75 ft/sec and runs toward first base at a rate of 24 ft/sec. At what rate does the distance between the ball and the batter change when 2 sec have passed?
40) [T] A batter hits a ball toward second base at 80 ft/sec and runs toward first base at a rate of 30 ft/sec. At what rate does the distance between the ball and the batter change when the runner has covered one-third of the distance to first base? (Hint: Recall the law of cosines.)
Solution: The distance is increasing at a rate of \(62.50\) ft/sec.
41) [T] A batter hits the ball and runs toward first base at a speed of 22 ft/sec. At what rate does the distance between the runner and second base change when the runner has run 30 ft?
42) [T] Runners start at first and second base. When the baseball is hit, the runner at first base runs at a speed of 18 ft/sec toward second base and the runner at second base runs at a speed of 20 ft/sec toward third base. How fast is the distance between runners changing 1 sec after the ball is hit?
Solution: The distance is decreasing at a rate of \(11.99\) ft/sec.
4.2: Linear Approximations and Differentials
1) What is the linear approximation for any generic linear function \(y=mx+b\)?
2) Determine the necessary conditions such that the linear approximation function is constant. Use a graph to prove your result.
Solution: \(f′(a)=0\)
3) Explain why the linear approximation becomes less accurate as you increase the distance between \(x\) and \(a\). Use a graph to prove your argument.
4) When is the linear approximation exact?
Solution: The linear approximation exact when \(y=f(x)\) is linear or constant.
For the following exercises, find the linear approximation \(L(x)\) to \(y=f(x)\) near \(x=a\) for the function.
5) [T] \(f(x)=x+x^4,a=0\)
6) [T] \(f(x)=\frac{1}{x},a=2\)
Solution: \(L(x)=\frac{1}{2}−\frac{1}{4}(x−2)\)
7) [T] \(f(x)=tanx,a=\frac{π}{4}\)
8) [T] \(f(x)=sinx,a=\frac{π}{2}\)
Solution: \(L(x)=1\)
9) [T] \(f(x)=xsinx,a=2π\)
10) [T] \(f(x)=sin^2x,a=0\)
Solution: \(L(x)=0\)
For the following exercises, compute the values given within 0.01 by deciding on the appropriate \(f(x)\) and \(a\), and evaluating \(L(x)=f(a)+f′(a)(x−a).\) Check your answer using a calculator.
11) [T] \((2.001)^6\)
12) [T] \(sin(0.02)\)
Solution: \(0.02\)
13) [T] \(cos(0.03)\)
14) [T] \((15.99)^{1/4}\)
Solution: \(1.9996875\)
15) [T] \(\frac{1}{0.98}\)
16) [T] \(sin(3.14)\)
Solution: \(0.001593\)
For the following exercises, determine the appropriate \(f(x)\) and \(a\), and evaluate \(L(x)=f(a)+f′(a)(x−a).\) Calculate the numerical error in the linear approximations that follow.
17) \((1.01)^3\)
18) \(cos(0.01)\)
Solution: \(1;\) error, \(~0.00005\)
19) \((sin(0.01))^2\)
20) \((1.01)^{−3}\)
Solution: \(0.97;\) error, \(~0.0006\)
21) \((1+\frac{1}{10})^{10}\)
22) \(\sqrt{8.99}\)
Solution: \(3−\frac{1}{600};\) error, \(~4.632×10^{−7}\)
For the following exercises, find the differential of the function.
23) \(y=3x^4+x^2−2x+1\)
24) \(y=xcosx\)
Solution: \(dy=(cosx−xsinx)dx\)
25) \(y=\sqrt{1+x}\)
26) \(y=\frac{x^2+2}{x−1}\)
Solution: \(dy=(\frac{x^2−2x−2}{(x−1)^2})dx\)
For the following exercises, find the differential and evaluate for the given \(x\) and \(dx\).
27) \(y=3x^2−x+6, x=2, dx=0.1\)
28) \(y=\frac{1}{x+1},x=1, dx=0.25\)
Solution: \(dy=−\frac{1}{(x+1)^2}dx,−\frac{1}{16}\)
29) \(y=tanx,x=0, dx=\frac{π}{10}\)
30) \(y=\frac{3x^2+2}{\sqrt{x+1}}\), x=0, dx=0.1\)
Solution: \(dy=\frac{9x^2+12x−2}{2(x+1)^{3/2}}dx,−0.1\)
31) \(y=\frac{sin(2x)}{x}, x=π, dx=0.25\)
32) \(y=x^3+2x+\frac{1}{x}, x=1, dx=0.05\)
Solution: \(dy=(3x^2+2−\frac{1}{x^2})dx, 0.2\)
For the following exercises, find the change in volume \(dV\) or in surface area \(dA.\)
33) \(dV\) if the sides of a cube change from 10 to 10.1.
34) \(dA\) if the sides of a cube change from \(x\) to \(x+dx\).
Solution: \(12xdx\)
35) \(dA\) if the radius of a sphere changes from \(r\) by \(dr.\)
36) \(dV\) if the radius of a sphere changes from \(r\) by \(dr\).
Solution: \(4πr^2dr\)
37) \(dV\) if a circular cylinder with \(r=2\) changes height from 3 cm to \(3.05cm.\)
38) \(dV\) if a circular cylinder of height 3 changes from \(r=2\) to \(r=1.9cm.\)
Solution: \(−1.2πcm^3\)
For the following exercises, use differentials to estimate the maximum and relative error when computing the surface area or volume.
39) A spherical golf ball is measured to have a radius of \(5mm,\) with a possible measurement error of \(0.1mm.\) What is the possible change in volume?
40) A pool has a rectangular base of 10 ft by 20 ft and a depth of 6 ft. What is the change in volume if you only fill it up to 5.5 ft?
Solution: \(−100 ft^3\)
41) An ice cream cone has height 4 in. and radius 1 in. If the cone is 0.1 in. thick, what is the difference between the volume of the cone, including the shell, and the volume of the ice cream you can fit inside the shell
For the following exercises, confirm the approximations by using the linear approximation at \(x=0.\)
42) \(\sqrt{1−x}≈1−\frac{1}{2}x\)
43) \(\frac{1}{\sqrt{1−x^2}}≈1\)
44) \(\sqrt{c^2+x^2}≈c\)
4.3: Maxima and Minima
1) In precalculus, you learned a formula for the position of the maximum or minimum of a quadratic equation \(y=ax^2+bx+c\), which was \(m=−\frac{b}{(2a)}\). Prove this formula using calculus.
2) If you are finding an absolute minimum over an interval \([a,b],\) why do you need to check the endpoints? Draw a graph that supports your hypothesis.
Solution: Answers may vary
3) If you are examining a function over an interval \((a,b),\) for \(a\) and \(b\) finite, is it possible not to have an absolute maximum or absolute minimum?
4) When you are checking for critical points, explain why you also need to determine points where \(f(x)\) is undefined. Draw a graph to support your explanation.
Solution: Answers will vary
5) Can you have a finite absolute maximum for \(y=ax^2+bx+c\) over \((−∞,∞)\)? Explain why or why not using graphical arguments.
6) Can you have a finite absolute maximum for \(y=ax^3+bx^2+cx+d\) over \((−∞,∞)\) assuming a is non-zero? Explain why or why not using graphical arguments.
Solution: No; answers will vary
7) Let \(m\) be the number of local minima and \(M\) be the number of local maxima. Can you create a function where \(M>m+2\)? Draw a graph to support your explanation.
8) Is it possible to have more than one absolute maximum? Use a graphical argument to prove your hypothesis.
Solution: Since the absolute maximum is the function (output) value rather than the x value, the answer is no; answers will vary
9) Is it possible to have no absolute minimum or maximum for a function? If so, construct such a function. If not, explain why this is not possible.
10) [T] Graph the function \(y=e^{ax}.\) For which values of \(a\), on any infinite domain, will you have an absolute minimum and absolute maximum?
Solution: When \(a=0\)
For the following exercises, determine where the local and absolute maxima and minima occur on the graph given. Assume domains are closed intervals unless otherwise specified.
11)
12)
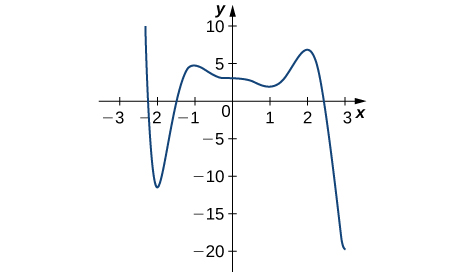
Solution: Absolute minimum at 3; Absolute maximum at −2.2; local minima at −2, 1; local maxima at −1, 2
13)
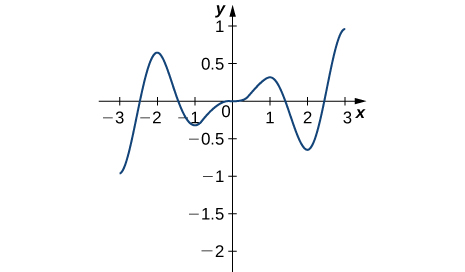
14)
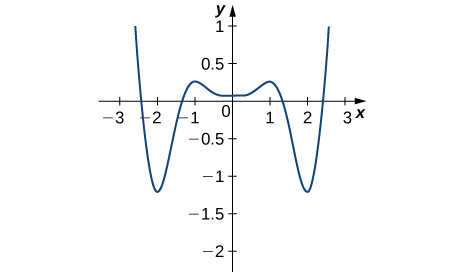
Solution: Absolute minima at −2, 2; absolute maxima at −2.5, 2.5; local minimum at 0; local maxima at −1, 1
For the following problems, draw graphs of \(f(x),\) which is continuous, over the interval \([−4,4]\) with the following properties:
15) Absolute maximum at \(x=2\) and absolute minima at \(x=±3\)
16) Absolute minimum at \(x=1\) and absolute maximum at \(x=2\)
Solution: Answers may vary.
17) Absolute maximum at \(x=4,\) absolute minimum at \(x=−1,\) local maximum at \(x=−2,\) and a critical point that is not a maximum or minimum at \(x=2\)
18) Absolute maxima at \(x=2\) and \(x=−3\), local minimum at \(x=1\), and absolute minimum at \(x=4\)
Solution: Answers may vary.
For the following exercises, find the critical points in the domains of the following functions.
19) \(y=4x^3−3x\)
20) \(y=4\sqrt{x}−x^2\)
Solution: \(x=1\)
21) \(y=\frac{1}{x−1}\)
22) \(y=ln(x−2)\)
Solution: None
23) \(y=tan(x)\)
24) \(y=\sqrt{4−x^2}\)
Solution: \(x=0\)
25) \(y=x^{3/2}−3x^{5/2}\)
26) \(y=\frac{x^2−1}{x^2+2x−3}\)
Solution: None
27) \(y=sin^2(x)\)
28) \(y=x+\frac{1}{x}\)
Solution: \(x=−1,1\)
For the following exercises, find the local and/or absolute maxima for the functions over the specified domain.
29) \(f(x)=x2^+3\) over \([−1,4]\)
30) \(y=x^2+\frac{2}{x}\) over \([1,4]\)
Solution: Absolute maximum: \(x=4, y=\frac{33}{2}\); absolute minimum: \(x=1, y=3\)
31) \(y=(x−x^2)^2\) over \([−1,1]\)
32) \(y=\frac{1}{(x−x^2)}\) over \([0,1]\)
Solution: Absolute minimum: \(x=\frac{1}{2}, y=4\)
33) \(y=\sqrt{9−x}\) over \([1,9]\)
34) \(y=x+sin(x)\) over \([0,2π]\)
Solution: Absolute maximum: \(x=2π, y=2π;\) absolute minimum: \(x=0, y=0\)
35) \(y=\frac{x}{1+x}\) over \([0,100]\)
36) \(y=|x+1|+|x−1|\) over \([−3,2]\)
Solution: Absolute maximum: \(x=−3;\) absolute minimum: \(−1≤x≤1, y=2\)
37) \(y=\sqrt{x}−\sqrt{x^3}\) over \([0,4]\)
38) \(y=sinx+cosx\) over \([0,2π]\)
Solution: Absolute maximum: \(x=\frac{π}{4}, y=\sqrt{2}\); absolute minimum: \(x=\frac{5π}{4}, y=−\sqrt{2}\)
39) \(y=4sinθ−3cosθ\) over \([0,2π]\)
For the following exercises, find the local and absolute minima and maxima for the functions over \((−∞,∞).\)
40) \(y=x^2+4x+5\)
Solution: Absolute minimum: \(x=−2, y=1\)
41) \(y=x^3−12x\)
42) \(y=3x^4+8x^3−18x^2\)
Solution: Absolute minimum: \(x=−3, y=−135;\) local maximum: \(x=0, y=0\); local minimum: \(x=1, y=−7\)
43) \(y=x^3(1−x)^6\)
44) \(y=\frac{x^2+x+6}{x−1}\)
Solution: Local maximum: \(x=1−2\sqrt{2}, y=3−4\sqrt{2}\); local minimum: \(x=1+2\sqrt{2}, y=3+4\sqrt{2}\)
45) \(y=\frac{x^2−1}{x−1}\)
For the following functions, use a calculator to graph the function and to estimate the absolute and local maxima and minima. Then, solve for them explicitly.
46) [T] \(y=3x\sqrt{1−x^2}\)
Solution: Absolute maximum: \(x=\frac{\sqrt{2}}{2}, y=\frac{3}{2};\) absolute minimum: \(x=−\frac{\sqrt{2}}{2}, y=−\frac{3}{2}\)
47) [T] \(y=x+sin(x)\)
48) [T] \(y=12x^5+45x^4+20x^3−90x^2−120x+3\)
Solution: Local maximum: \(x=−2,y=59\); local minimum: \(x=1, y=−130\)
49) [T] \(y=\frac{x^3+6x^2−x−30}{x−2}\)
50) [T] \(y=\frac{\sqrt{4−x^2}}{\sqrt{4+x^2}}\)
Solution: Absolute maximum: \(x=0, y=1;\) absolute minimum: \(x=−2,2, y=0\)
51) A company that produces cell phones has a cost function of \(C=x^2−1200x+36,400,\) where \(C\) is cost in dollars and \(x\) is number of cell phones produced (in thousands). How many units of cell phone (in thousands) minimizes this cost function?
52) A ball is thrown into the air and its position is given by \(h(t)=−4.9t^2+60t+5m.\) Find the height at which the ball stops ascending. How long after it is thrown does this happen?
Solution: \(h=\frac{9245}{49}m, t=\frac{300}{49}s\)
For the following exercises, consider the production of gold during the California gold rush (1848–1888). The production of gold can be modeled by \(G(t)=\frac{(25t)}{(t^2+16)}\), where t is the number of years since the rush began \((0≤t≤40)\) and \(G\) is ounces of gold produced (in millions). A summary of the data is shown in the following figure.
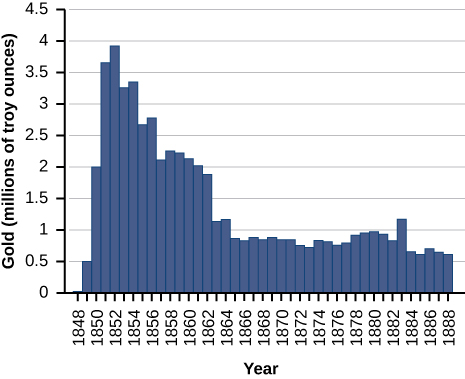
53) Find when the maximum (local and global) gold production occurred, and the amount of gold produced during that maximum.
54) Find when the minimum (local and global) gold production occurred. What was the amount of gold produced during this minimum?
Solution: The global minimum was in 1848, when no gold was produced.
Find the critical points, maxima, and minima for the following piecewise functions.
55) \(y=\begin{cases}x^2−4x& 0≤x≤1//x^2−4&1<x≤2\end{cases}\)
56) \(y=\begin{cases}x^2+1 & x≤1 // x^2−4x+5 & x>1\end{cases}\)
Solution: Absolute minima: \(x=0, x=2, y=1\); local maximum at \(x=1, y=2\)
For the following exercises, find the critical points of the following generic functions. Are they maxima, minima, or neither? State the necessary conditions.
57) \(y=ax^2+bx+c,\) given that \(a>0\)
58) \(y=(x−1)^a\), given that \(a>1\)
Solution: No maxima/minima if \(a\) is odd, minimum at \(x=1\) if \(a\) is even
4.4: The Mean Value Theorem
1)Why do you need continuity to apply the Mean Value Theorem? Construct a counterexample.
2) Why do you need differentiability to apply the Mean Value Theorem? Find a counterexample.
Solution: One example is \(f(x)=|x|+3,−2≤x≤2\)
3) When are Rolle’s theorem and the Mean Value Theorem equivalent?
4) If you have a function with a discontinuity, is it still possible to have \(f′(c)(b−a)=f(b)−f(a)?\) Draw such an example or prove why not.
Solution: Yes, but the Mean Value Theorem still does not apply
For the following exercises, determine over what intervals (if any) the Mean Value Theorem applies. Justify your answer.
5) \(y=sin(πx)\)
6) \(y=\frac{1}{x^3}\)
Solution: \((−∞,0),(0,∞)\)
7) \(y=\sqrt{4−x^2}\)
8) \(y=\sqrt{x^2−4}\)
Solution: \((−∞,−2),(2,∞)\)
9) \(y=ln(3x−5)\)
For the following exercises, graph the functions on a calculator and draw the secant line that connects the endpoints. Estimate the number of points \(c\) such that \(f′(c)(b−a)=f(b)−f(a).\)
10) [T] \(y=3x^3+2x+1\) over \([−1,1]\)
Solution: 2 points
11) [T] \(y=tan(\frac{π}{4}x)\) over \([−\frac{3}{2},\frac{3}{2}]\)
12) [T] \(y=x^2cos(πx)\) over \([−2,2]\)
Solution: 5 points
13) [T] \(y=x^6−\frac{3}{4}x^5−\frac{9}{8}x^4+\frac{15}{16}x^3+\frac{3}{32}x^2+\frac{3}{16}x+\frac{1}{32}\) over \([−1,1]\)
For the following exercises, use the Mean Value Theorem and find all points \(0<c<2\) such that \(f(2)−f(0)=f′(c)(2−0)\).
14) \(f(x)=x^3\)
Solution: \(c=\frac{2\sqrt{3}}{3}\)
15) \(f(x)=sin(πx)\)
16) \(f(x)=cos(2πx)\)
Solution: \(c=\frac{1}{2},1,\frac{3}{2}\)
17) \(f(x)=1+x+x^2\)
18) \(f(x)=(x−1)^{10}\)
Solution: \(c=1\)
19) \(f(x)=(x−1)^9\)
For the following exercises, show there is no \(c\) such that \(f(1)−f(−1)=f′(c)(2)\). Explain why the Mean Value Theorem does not apply over the interval \([−1,1].\)
20) \(f(x)=∣x−\frac{1}{2} ∣\)
Solution: Not differentiable
21) \(f(x)=\frac{1}{x^2}\)
22) \(f(x)=\sqrt{|x|}\)
Solution: Not differentiable
23) \(f(x)=[x]\) (Hint: This is called the floor function and it is defined so that \(f(x)\) is the largest integer less than or equal to \(x\).)
For the following exercises, determine whether the Mean Value Theorem applies for the functions over the given interval \(([a,b]\. Justify your answer.
24) \(y=e^x\) over \([0,1]\)
Solution: Yes
25) \(y=ln(2x+3)\) over \([−\frac{3}{2},0]\)
26) \(f(x)=tan(2πx)\) over \([0,2]\)
Solution: The Mean Value Theorem does not apply since the function is discontinuous at \(x=\frac{1}{4},\frac{3}{4},\frac{5}{4},\frac{7}{4}.\)
27) \(y=\sqrt{9−x^2}\) over \([−3,3]\)
28) \(y=\frac{1}{|x+1|}\) over \([0,3]\)
Solution: Yes
29) \(y=x^3+2x+1\) over \([0,6]\)
30) \(y=\frac{x^2+3x+2}{x}\) over \([−1,1]\)
Solution: The Mean Value Theorem does not apply; discontinuous at \(x=0.\)
31) \(y=\frac{x}{sin(πx)+1}\) over \([0,1]\)
32) \(y=ln(x+1)\) over \([0,e−1]\)
Yes
33) \(y=xsin(πx)\) over \([0,2]\)
34) \(y=5+|x|\) over \([−1,1]\)
Solution: The Mean Value Theorem does not apply; not differentiable at \(x=0\).
For the following exercises, consider the roots of the equation.
35) Show that the equation \(y=x^3+3x^2+16\) has exactly one real root. What is it?
36) Find the conditions for exactly one root (double root) for the equation \(y=x^2+bx+c\)
Solution: \(b=±2\sqrt{c}\)
37) Find the conditions for \(y=e^x−b\) to have one root. Is it possible to have more than one root?
For the following exercises, use a calculator to graph the function over the interval \([a,b]\) and graph the secant line from \(a\) to \(b\). Use the calculator to estimate all values of \(c\) as guaranteed by the Mean Value Theorem. Then, find the exact value of \(c\), if possible, or write the final equation and use a calculator to estimate to four digits.
38) [T] \(y=tan(πx)\) over \([−\frac{1}{4},\frac{1}{4}]\)
Solution: \(c=±\frac{1}{π}cos^{−1}(\frac{\sqrt{π}}{2}), c=±0.1533\)
39) [T] \(y=\frac{1}{\sqrt{x+1}}\) over \([0,3]\)
40) [T] \(y=∣x^2+2x−4∣\) over \([−4,0]\)
Solution: The Mean Value Theorem does not apply.
41) [T] \(y=x+\frac{1}{x}\) over \([\frac{1}{2},4]\)
42) [T] \(y=\sqrt{x+1}+\frac{1}{x^2}\) over \([3,8]\)
Solution: \(\frac{1}{2\sqrt{c+1}}−\frac{2}{c^3}=\frac{521}{2880}; c=3.133,5.867\)
43) At 10:17 a.m., you pass a police car at 55 mph that is stopped on the freeway. You pass a second police car at 55 mph at 10:53 a.m., which is located 39 mi from the first police car. If the speed limit is 60 mph, can the police cite you for speeding?
44) Two cars drive from one spotlight to the next, leaving at the same time and arriving at the same time. Is there ever a time when they are going the same speed? Prove or disprove.
Solution: Yes
45) Show that \(y=sec^2x\) and \(y=tan^2x\) have the same derivative. What can you say about \(y=sec^2x−tan^2x\)?
46) Show that \(y=csc^2x\) and \(y=cot^2x\) have the same derivative. What can you say about \(y=csc^2x−cot^2x\)?
Solution: It is constant.
4.5: Derivatives and the Shape of a Graph
1) If c is a critical point of \(f(x)\), when is there no local maximum or minimum at \(c\)? Explain.
2) For the function \(y=x^3\), is \(x=0\) both an inflection point and a local maximum/minimum?
Solution: It is not a local maximum/minimum because \(f′\) does not change sign
3) For the function \(y=x^3\), is \(x=0\) an inflection point?
4) Is it possible for a point \(c\) to be both an inflection point and a local extrema of a twice differentiable function?
Solution: No
6) Why do you need continuity for the first derivative test? Come up with an example.
7) Explain whether a concave-down function has to cross \(y=0\) for some value of \(x\).
Solution: False; for example, \(y=\sqrt{x}\).
8) Explain whether a polynomial of degree \(2\) can have an inflection point.
For the following exercises, analyze the graphs of \(f′\), then list all intervals where f is increasing or decreasing.
9)
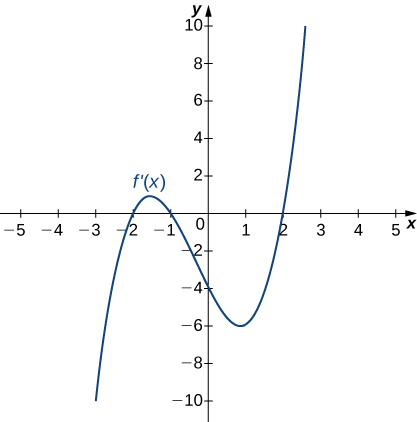
Solution: Increasing for \(−2<x<−1\) and \(x>2\); decreasing for \(x<−2\) and \(−1<x<2\)
10)
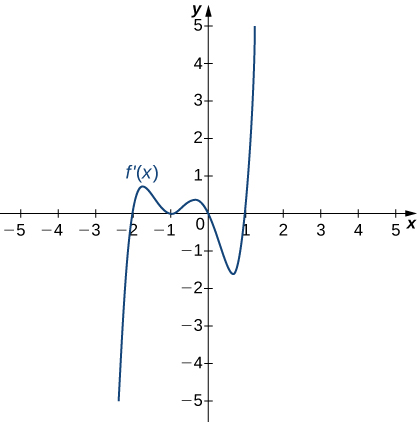
11)
Solution: Decreasing for \(x<1\), increasing for \(x>1\)
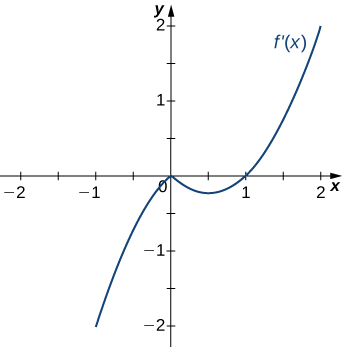
12)
13)
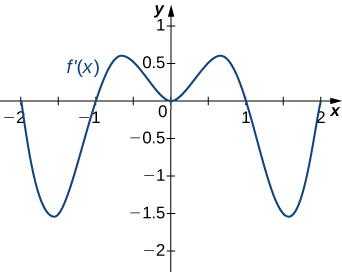
Solution: Decreasing for \(−2<x<−1\) and \(1<x<2\); increasing for \(−1<x<1\) and \(x<−2\) and \(x>2\)
For the following exercises, analyze the graphs of \(f′,\) then list all intervals where
a. \(f\) is increasing and decreasing and
b. the minima and maxima are located.
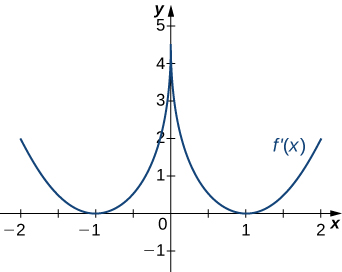
14)
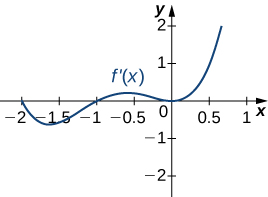
15)
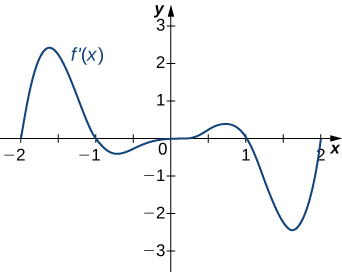
Solution: a. Increasing over \(−2<x<−1,0<x<1,x>2\), decreasing over \(x<−2, −1<x<0,1<x<2;\) b. maxima at \(x=−1\) and \(x=1\), minima at \(x=−2\) and \(x=0\) and \(x=2\)
16)
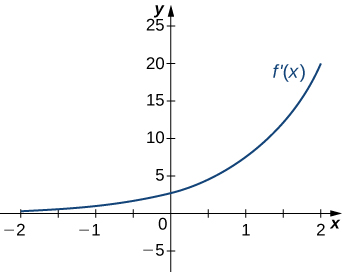
17)
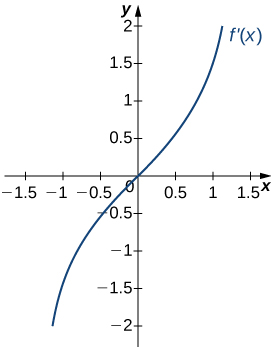
Solution: a. Increasing over \(x>0\), decreasing over \(x<0;\) b. Minimum at \(x=0\)
18)
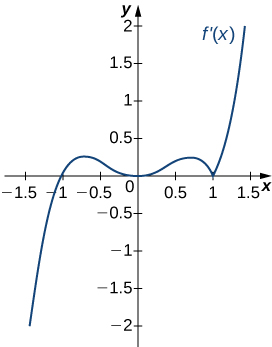
For the following exercises, analyze the graphs of \(f′\), then list all inflection points and intervals \(f\) that are concave up and concave down.
19)
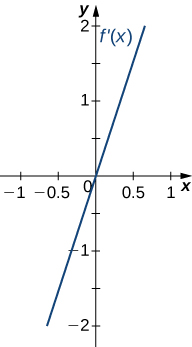
Solution: Concave up on all \(x\), no inflection points
20)
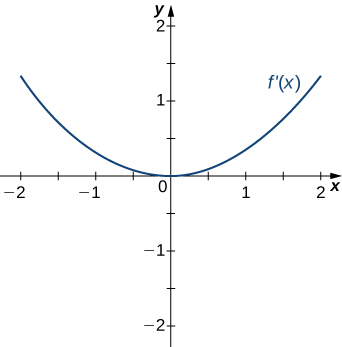
21)
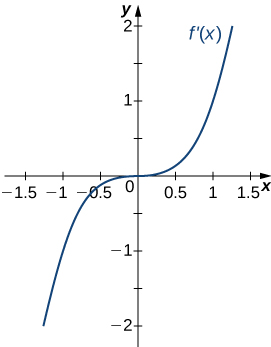
Solution: Concave up on all \(x\), no inflection points
22)
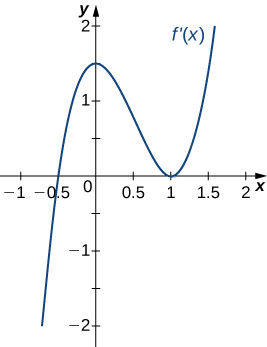
23)
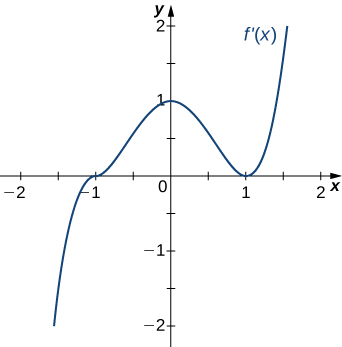
Solution: Concave up for \(x<0\) and \(x>1\), concave down for \(0<x<1\), inflection points at \(x=0\) and \(x=1\)
For the following exercises, draw a graph that satisfies the given specifications for the domain \(x=[−3,3].\) The function does not have to be continuous or differentiable.
24) \(f(x)>0,f′(x)>0\) over \(x>1,−3<x<0,f′(x)=0\) over \(0<x<1\)
25) \(f′(x)>0\) over \(x>2,−3<x<−1,f′(x)<0\) over \(−1<x<2,f''(x)<0\) for all \(x\)
Solution: Answer will vary
26) \(f''(x)<0\) over \(−1<x<1,f''(x)>0,−3<x<−1,1<x<3,\) local maximum at \(x=0,\) local minima at \(x=±2\)
27) There is a local maximum at \(x=2,\) local minimum at \(x=1,\) and the graph is neither concave up nor concave down.
Solution: Answers will vary
28) There are local maxima at \(x=±1,\) the function is concave up for all \(x\), and the function remains positive for all \(x.\)
For the following exercises, determine
a. intervals where \(f\) is increasing or decreasing and
b. local minima and maxima of \(f\).
29) \(f(x)=sinx+sin^3x\) over −π<x<π
Solution:
a. Increasing over \(−\frac{π}{2}<x<\frac{π}{2},\) decreasing over \(x<−π\frac{π}{2},x>\frac{π}{2}\)
b. Local maximum at \(x=\frac{π}{2}\); local minimum at \(x=−\frac{π}{2}\)
28) \(f(x)=x^2+cosx\)
For the following exercises, determine a. intervals where \(f\) is concave up or concave down, and b. the inflection points of \(f\).
29) \(f(x)=x^3−4x^2+x+2\)
Solution:
a. Concave up for \(x>\frac{4}{3},\) concave down for \(x<\frac{34}{3}\)
b. Inflection point at \(x=\frac{4}{3}\)
For the following exercises, determine
a. intervals where \(f\) is increasing or decreasing,
b. local minima and maxima of \(f\),
c. intervals where \(f\) is concave up and concave down, and
d. the inflection points of \(f.\)
30) \(f(x)=x^2−6x\)
31) \(f(x)=x^3−6x^2\)
Solution: a. Increasing over \(x<0\) and \(x>4,\) decreasing over \(0<x<4\) b. Maximum at \(x=0\), minimum at \(x=4\) c. Concave up for \(x>2\), concave down for \(x<2\) d. Infection point at \(x=2\)
32) \(f(x)=x^4−6x^3\)
33) \(f(x)=x^{11}−6x^{10}\)
Solution: a. Increasing over \(x<0\) and \(x>\frac{60}{11}\), decreasing over \(0<x<\frac{60}{11}\) b. Minimum at \(x=\frac{60}{11}\) c. Concave down for \(x<\frac{54}{11}\), concave up for \(x>\frac{54}{11}\) d. Inflection point at \(x=\frac{54}{11}\)
34) \(f(x)=x+x^2−x^3\)
35) \(f(x)=x^2+x+1\)
Solution: a. Increasing over \(x>−\frac{1}{2}\), decreasing over \(x<−\frac{1}{2}\) b. Minimum at \(x=−\frac{1}{2}\) c. Concave up for all \(x\) d. No inflection points
36) \(f(x)=x^3+x^4\)
For the following exercises, determine
a. intervals where \(f\) is increasing or decreasing,
b. local minima and maxima of \(f,\)
c. intervals where \(f\) is concave up and concave down, and
d. the inflection points of \(f.\) Sketch the curve, then use a calculator to compare your answer. If you cannot determine the exact answer analytically, use a calculator.
37) [T] \(f(x)=sin(πx)−cos(πx)\) over \(x=[−1,1]\)
Solution: a. Increases over \(−\frac{1}{4}<x<\frac{3}{4},\) decreases over \(x>\frac{3}{4}\) and \(x<−\frac{1}{4}\) b. Minimum at \(x=−\frac{1}{4}\), maximum at \(x=\frac{3}{4}\) c. Concave up for \(−\frac{3}{4}<x<\frac{1}{4}\), concave down for \(x<−\frac{3}{4}\) and \(x>\frac{1}{4}\) d. Inflection points at \(x=−\frac{3}{4},x=\frac{1}{4}\)
38) [T] \(f(x)=x+sin(2x)\) over \(x=[−\frac{π}{2},\frac{π}{2}]\)
39) [T] \(f(x)=sinx+tanx\) over \((−\frac{π}{2},\frac{π}{2})\)
Solution: a. Increasing for all \(x\) b. No local minimum or maximum c. Concave up for \(x>0\), concave down for \(x<0\) d. Inflection point at \(x=0\)
40) [T] \(f(x)=(x−2)^2(x−4)^2\)
41) [T] \(f(x)=\frac{1}{1−x},x≠1\)
Solution: a. Increasing for all \(x\) where defined b. No local minima or maxima c. Concave up for \(x<1\); concave down for \(x>1\) d. No inflection points in domain
42) [T] \(f(x)=\frac{sinx}{x}\) over \(x=[−2π,2π] [2π,0)∪(0,2π]\)
43) \(f(x)=sin(x)e^x\) over \(x=[−π,π]\)
Solution: a. Increasing over \(−\frac{π}{4}<x<\frac{3π}{4}\), decreasing over \(x>\frac{3π}{4},x<−\frac{π}{4}\) b. Minimum at \(x=−\frac{π}{4}\), maximum at \(x=\frac{3π}{4}\) c. Concave up for \(−\frac{π}{2}<x<\frac{π}{2}\), concave down for \(x<−\frac{π}{2},x>\frac{π}{2}\) d. Infection points at \(x=±\frac{π}{2}\)
44) \(f(x)=lnx\sqrt{x},x>0\)
45) \(f(x)=\frac{1}{4}\sqrt{x}+\frac{1}{x},x>0\)
Solution: a. Increasing over \(x>4,\) decreasing over \(0<x<4\) b. Minimum at \(x=4\) c. Concave up for \(0<x<8\sqrt[3]{2}\), concave down for \(x>8\sqrt[3]{2}\) d. Inflection point at \(x=8\sqrt[3]{2}\)
46) \(f(x)=\frac{e^x}{x},x≠0\)
For the following exercises, interpret the sentences in terms of \(f,f′,\) and \(f''.\)
47) The population is growing more slowly. Here \(f\) is the population.
Solution: \(f>0,f′>0,f''<0\)
48) A bike accelerates faster, but a car goes faster. Here \(f=\) Bike’s position minus Car’s position.
49) The airplane lands smoothly. Here \(f\) is the plane’s altitude.
Solution: \(f>0,f′<0,f''<0\)
50) Stock prices are at their peak. Here \(f\)is the stock price.
51) The economy is picking up speed. Here \(f\) is a measure of the economy, such as GDP.
Solution: \(f>0,f′>0,f''>0\)
For the following exercises, consider a third-degree polynomial \(f(x),\) which has the properties f′(1)=0,f′(3)=0.
Determine whether the following statements are true or false. Justify your answer.
52) \(f(x)=0\) for some \(1≤x≤3\)
53) \(f''(x)=0\) for some \(1≤x≤3\)
Soltuion: True, by the Mean Value Theorem
54) There is no absolute maximum at \(x=3\)
55) If \(f(x)\) has three roots, then it has \(1\) inflection point.
Solution: True, examine derivative
56) If \(f(x)\) has one inflection point, then it has three real roots.

