3.9 E: Derivatives Ln, etc. Exercises

Last updated
Save as PDF

Page ID: 10870

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

3.9: Derivatives of Ln, General Exponent & Log Functions; and Logarithmic Differentiation

Exercise:

For the following exercises, find \(f′(x)\) for each function.

333) \(f(x)=e^{x^3\ln x}\)

Answer:: \(e^{x^3}\ln x(3x^2\ln x+x^2)\)

336) \(f(x)=\frac{10^x}{\ln10}\)

337) \(f(x)=2^{4x}+4x^2\)

Answer:: \(2^{4x+2}⋅\ln 2+8x\)

338) \(f(x)=3^{\sin(3x)}\)

339) \(f(x)=x^π⋅π^x\)

Answer:: \(πx^{π−1}⋅π^x+x^π⋅π^x\ln π\)

340) \(f(x)=\ln(4x^3+x)\)

341) \(f(x)=\ln\sqrt{5x−7}\)

Answer:: \(\frac{5}{2(5x−7)}\)

342) \(f(x)=x^2\ln(9x)\)

343) \(f(x)=log(\sec x)\)

Answer:: \(\frac{\tan x}{\ln10}\)

344) \(f(x)=log_7(6x^4+3)^5\)

345) \(f(x)=2^x⋅log_37^{x^2−4}\)

Answer:: \(2^x⋅\ln 2⋅log_37^{x^2−4}+2^x⋅\frac{2x\ln 7}{\ln 3}\)

For the following exercises, use logarithmic differentiation to find \(\frac{dy}{dx}\).

346) \(y=x^{\sqrt{x}}\)

347) \(y=(\sin(2x))^{4x}\)

Answer:: \((\sin(2x))^{4x}[4⋅ln(\sin(2x))+8x⋅\cot(2x)]\)

348) \(y=(\ln x)^{\ln x}\)

349) \(y=x^{log_2x}\)

Answer:: \(x^{log_2x}⋅\frac{2\ln x}{x\ln 2}\)

350) \(y=(x^2−1)^{\ln x}\)

351) \(y=x^{\cot x}\)

Answer:: \(x^{\cot x}⋅[−\csc^2x⋅lnx+\frac{\cot x}{x}]\)

352) \(y=\frac{x+11}{\sqrt[3]{x^2−4}}\)

353) \(y=x^{−1/2}(x^2+3)^{2/3}(3x−4)^4\)

Answer:: \(x^{−1/2}(x^2+3)^{2/3}(3x−4)^4⋅[\frac{−1}{2x}+\frac{4x}{3(x^2+3)}+\frac{12}{3x−4}]\)

354) [T] Find an equation of the tangent line to the graph of \(f(x)=4xe^{(x^2−1)}\) at the point where

\(x=−1.\) Graph both the function and the tangent line.

355) [T] Find the equation of the line that is normal to the graph of \(f(x)=x⋅5^x\) at the point where \(x=1\). Graph both the function and the normal line.

Answer:

\(y=\frac{−1}{5+5\ln 5}x+(5+\frac{1}{5+5\ln 5})\)

356) [T] Find the equation of the tangent line to the graph of \(x^3−x\ln y+y^3=2x+5\) at the point where \(x=2\). (Hint: Use implicit differentiation to find \(\frac{dy}{dx}\).) Graph both the curve and the tangent line.

J357)

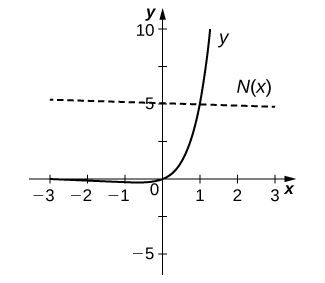
use the graph of \(y=f(x)\) (shown below) to

a. sketch the graph of \(y=f^{−1}(x)\), and

b. use part a. to estimate \((f^{−1})′(1)\).

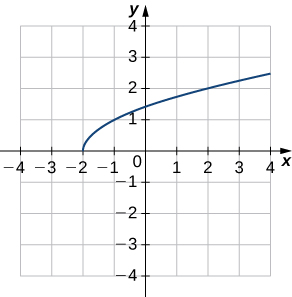
Answer:

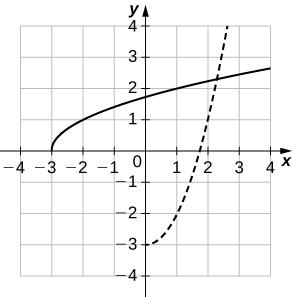
b. \((f^{−1})′(1)~2\)

For the next set of exercises, find \(\frac{dy}{dx}\). [Hint: first take the ln of both sides.]

J358) \(y=\frac{(2x^3−15x)\sqrt{6x^{4}+7}}{3x^2−x+3}\)

J359) \(y={30x^4}\sqrt{17x+2}{(\sin(x))}\)

J360) \(y={e^{5x}}{(3x-1)^\frac{2}{3}}{(8^{3x})}\)