3.4: Product & Quotient Rules
( \newcommand{\kernel}{\mathrm{null}\,}\)
The Product Rule
Now that we have examined the basic rules, we can begin looking at some of the more advanced rules. The first one examines the derivative of the product of two functions. Although it might be tempting to assume that the derivative of the product is the product of the derivatives, similar to the sum and difference rules, the product rule does not follow this pattern. To see why we cannot use this pattern, consider the function
Product Rule
Let
That is,
This means that the derivative of a product of two functions is the derivative of the first function times the second function plus the derivative of the second function times the first function.
Proof
We begin by assuming that
By applying the limit definition of the derivative to
By adding and subtracting
After breaking apart this quotient and applying the sum law for limits, the derivative becomes
Rearranging, we obtain
By using the continuity of
□
Example
For
Solution
Since
Example
For
Solution
If we set
Simplifying, we have
To check, we see that
Exercise
Use the product rule to obtain the derivative of
- Hint
-
Set
- Answer
-
The Quotient Rule
Having developed and practiced the product rule, we now consider differentiating quotients of functions. As we see in the following theorem, the derivative of the quotient is not the quotient of the derivatives; rather, it is the derivative of the function in the numerator times the function in the denominator minus the derivative of the function in the denominator times the function in the numerator, all divided by the square of the function in the denominator. In order to better grasp why we cannot simply take the quotient of the derivatives, keep in mind that
The Quotient Rule
Let
That is, if
then
The proof of the quotient rule is very similar to the proof of the product rule, so it is omitted here. Instead, we apply this new rule for finding derivatives in the next example.
Example
Use the quotient rule to find the derivative of
Solution
Let
Simplifying, we obtain
Exercise
Find the derivative of
- Answer
-
Apply the quotient rule with
- Answer
-
It is now possible to use the quotient rule to extend the power rule to find derivatives of functions of the form
Extended Power Rule
If
Proof
If
Simplifying, we see that
Finally, observe that since
□
Example
Find
Solution
By applying the extended power rule with
Example
Use the extended power rule and the constant multiple rule to find
Solution
It may seem tempting to use the quotient rule to find this derivative, and it would certainly not be incorrect to do so. However, it is far easier to differentiate this function by first rewriting it as
Exercise
Find the derivative of
- Hint
-
\Rewrite
- Answer
-
Combining Differentiation Rules
As we have seen throughout the examples in this section, it seldom happens that we are called on to apply just one differentiation rule to find the derivative of a given function. At this point, by combining the differentiation rules, we may find the derivatives of any polynomial or rational function. Later on we will encounter more complex combinations of differentiation rules. A good rule of thumb to use when applying several rules is to apply the rules in reverse of the order in which we would evaluate the function.
Example
For
Solution: Finding this derivative requires the sum rule, the constant multiple rule, and the product rule.
| Apply the sum rule. | |
| Apply the constant multiple rule todifferentiate |
|
Example
For
Solution
We can think of the function
Example
For
Solution
This procedure is typical for finding the derivative of a rational function.
Exercise
Find
- Hint
-
Apply the difference rule and the constant multiple rule.
- Answer
-
Example
Determine the values of
Solution
To find the values of
Since
we must solve
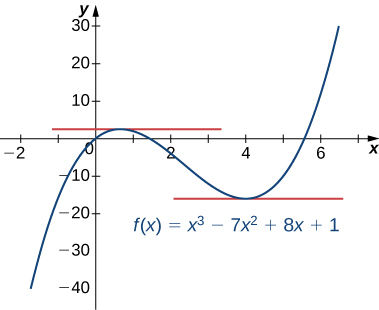
Figure
Example
The position of an object on a coordinate axis at time
Solution
Since the initial velocity is
After evaluating, we see that
Exercise
Find the values of x for which the line tangent to the graph of
- Hint
-
Solve
- Answer
-
Formula One Grandstands
Formula One car races can be very exciting to watch and attract a lot of spectators. Formula One track designers have to ensure sufficient grandstand space is available around the track to accommodate these viewers. However, car racing can be dangerous, and safety considerations are paramount. The grandstands must be placed where spectators will not be in danger should a driver lose control of a car (Figure).

Figure
Safety is especially a concern on turns. If a driver does not slow down enough before entering the turn, the car may slide off the racetrack. Normally, this just results in a wider turn, which slows the driver down. But if the driver loses control completely, the car may fly off the track entirely, on a path tangent to the curve of the racetrack.
Suppose you are designing a new Formula One track. One section of the track can be modeled by the function
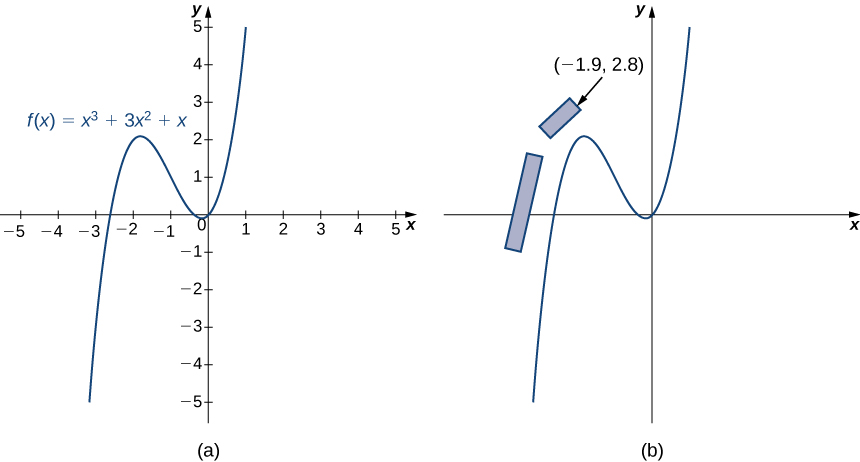
Figure
- Physicists have determined that drivers are most likely to lose control of their cars as they are coming into a turn, at the point where the slope of the tangent line is 1. Find the
- Find the equation of the tangent line to the curve at this point.
- To determine whether the spectators are in danger in this scenario, find the x-coordinate of the point where the tangent line crosses the line
- What if a driver loses control earlier than the physicists project? Suppose a driver loses control at the point (
- If a driver loses control as described in part 4, are the spectators safe?
- Should you proceed with the current design for the grandstand, or should the grandstands be moved?
Key Concepts
- The derivative of a product of two functions is the derivative of the first function times the second function plus the derivative of the second function times the first function.
- The derivative of the quotient of two functions is the derivative of the first function times the second function minus the derivative of the second function times the first function, all divided by the square of the second function.
- We used the limit definition of the derivative to develop formulas that allow us to find derivatives without resorting to the definition of the derivative. These formulas can be used singly or in combination with each other.
Glossary
- product rule
- the derivative of a product of two functions is the derivative of the first function times the second function plus the derivative of the second function times the first function:
- quotient rule
- the derivative of the quotient of two functions is the derivative of the first function times the second function minus the derivative of the second function times the first function, all divided by the square of the second function:
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


