2.5E: Exercises for Section 2.5

Last updated
Save as PDF

Page ID: 50132

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

For exercises 1 - 5, examine the graphs. Identify where the vertical asymptotes are located.

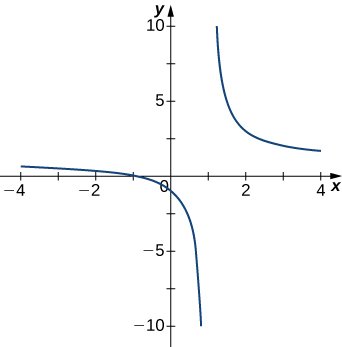
$The function graphed decreases very rapidly as it approaches x = 1 from the left, and on the other side of x = 1, it seems to start near infinity and then decrease rapidly.$

Answer: $x=1$

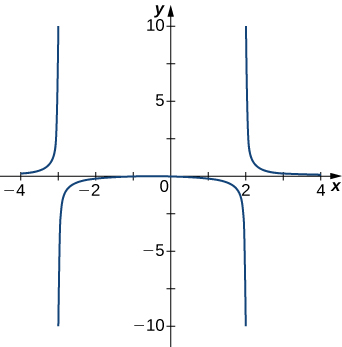
$The function graphed increases very rapidly as it approaches x = −3 from the left, and on the other side of x = −3, it seems to start near negative infinity and then increase rapidly to form a sort of U shape that is pointing down, with the other side of the U being at x = 2. On the other side of x = 2, the graph seems to start near infinity and then decrease rapidly.$

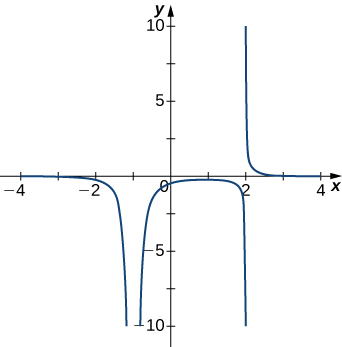
$The function graphed decreases very rapidly as it approaches x = −1 from the left, and on the other side of x = −1, it seems to start near negative infinity and then increase rapidly to form a sort of U shape that is pointing down, with the other side of the U being at x = 2. On the other side of x = 2, the graph seems to start near infinity and then decrease rapidly.$

Answer: $x=−1,\;x=2$

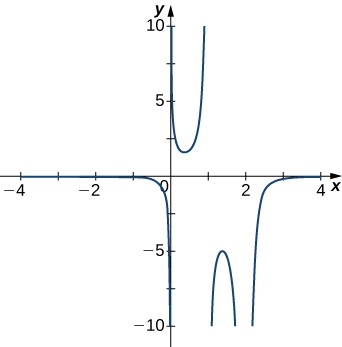
$The function graphed decreases very rapidly as it approaches x = 0 from the left, and on the other side of x = 0, it seems to start near infinity and then decrease rapidly to form a sort of U shape that is pointing up, with the other side of the U being at x = 1. On the other side of x = 1, there is another U shape pointing down, with its other side being at x = 2. On the other side of x = 2, the graph seems to start near negative infinity and then increase rapidly.$

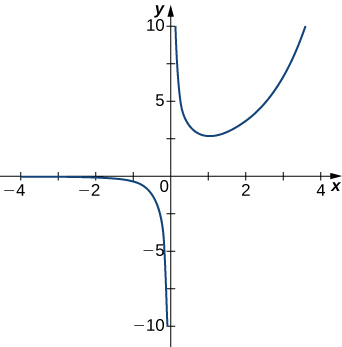
$The function graphed decreases very rapidly as it approaches x = 0 from the left, and on the other side of x = 0, it seems to start near infinity and then decrease rapidly to form a sort of U shape that is pointing up, with the other side being a normal function that appears as if it will take the entirety of the values of the x-axis.$

Answer: $x=0$

For the functions $f(x)$ in exercises 6 - 10, determine whether there is an asymptote at $x=a$. Justify your answer without graphing on a calculator.

6) $f(x)=\dfrac{x+1}{x^2+5x+4},\quad a=−1$

7) $f(x)=\dfrac{x}{x−2},\quad a=2$

Answer: Yes, there is a vertical asymptote at $x = 2$.

8) $f(x)=(x+2)^{3/2},\quad a=−2$

9) $f(x)=(x−1)^{−1/3},\quad a=1$

Answer: Yes, there is vertical asymptote at $x = 1$.

10) $f(x)=1+x^{−2/5},\quad a=1$

In exercises 11 - 20, evaluate the limit.

11) $\displaystyle \lim_{x→∞}\frac{1}{3x+6}$

Answer: $\displaystyle \lim_{x→∞}\frac{1}{3x+6} = 0$

12) $\displaystyle \lim_{x→∞}\frac{2x−5}{4x}$

13) $\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2}$

Answer: $\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2} = ∞$

14) $\displaystyle \lim_{x→−∞}\frac{3x^3−2x}{x^2+2x+8}$

15) $\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4}$

Answer: $\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4} = −\frac{1}{7}$

16) $\displaystyle \lim_{x→∞}\frac{3x}{\sqrt{x^2+1}}$

17) $\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2}$

Answer: $\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2} = -2$

18) $\displaystyle \lim_{x→∞}\frac{4x}{\sqrt{x^2−1}}$

19) $\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}}$

Answer: $\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}} = -4$

20) $\displaystyle \lim_{x→∞}\frac{2\sqrt{x}}{x−\sqrt{x}+1}$

For exercises 21 - 25, find the horizontal and vertical asymptotes.

21) $f(x)=x−\dfrac{9}{x}$

Answer: Horizontal: none,
Vertical: $x=0$

22) $f(x)=\dfrac{1}{1−x^2}$

23) $f(x)=\dfrac{x^3}{4−x^2}$

Answer: Horizontal: none,
Vertical: $x=±2$

24) $f(x)=\dfrac{x^2+3}{x^2+1}$

25) $f(x)=\sin(x)\sin(2x)$

Answer: Horizontal: none,
Vertical: none

26) $f(x)=\cos x+\cos(3x)+\cos(5x)$

27) $f(x)=\dfrac{x\sin(x)}{x^2−1}$

Answer: Horizontal: $y=0,$
Vertical: $x=±1$

28) $f(x)=\dfrac{x}{\sin(x)}$

29) $f(x)=\dfrac{1}{x^3+x^2}$

Answer: Horizontal: $y=0,$
Vertical: $x=0$ and $x=−1$

30) $f(x)=\dfrac{1}{x−1}−2x$

31) $f(x)=\dfrac{x^3+1}{x^3−1}$

Answer: Horizontal: $y=1,$
Vertical: $x=1$

32) $f(x)=\dfrac{\sin x+\cos x}{\sin x−\cos x}$

33) $f(x)=x−\sin x$

Answer: Horizontal: none,
Vertical: none

34) $f(x)=\dfrac{1}{x}−\sqrt{x}$

For exercises 35 - 38, construct a function $f(x)$ that has the given asymptotes.

35) $x=1$ and $y=2$

Answer: Answers will vary, for example: $y=\dfrac{2x}{x−1}$

36) $x=1$ and $y=0$

37) $y=4, \;x=−1$

Answer: Answers will vary, for example: $y=\dfrac{4x}{x+1}$

38) $x=0$

In exercises 39 - 43, graph the function on a graphing calculator on the window $x=[−5,5]$ and estimate the horizontal asymptote or limit. Then, calculate the actual horizontal asymptote or limit.

39) [T] $f(x)=\dfrac{1}{x+10}$

Answer: $\displaystyle \lim_{x→∞}\frac{1}{x+10}=0$ so $f$ has a horizontal asymptote of $y=0$.

40) [T] $f(x)=\dfrac{x+1}{x^2+7x+6}$

41) [T] $\displaystyle \lim_{x→−∞}x^2+10x+25$

Answer: $\displaystyle \lim_{x→−∞}x^2+10x+25 = ∞$

42) [T] $\displaystyle \lim_{x→−∞}\frac{x+2}{x^2+7x+6}$

43) [T] $\displaystyle \lim_{x→∞}\frac{3x+2}{x+5}$

Answer: $\displaystyle \lim_{x→∞}\frac{3x+2}{x+5}=3$ so this function has a horizontal asymptote of $y=3$.

Contributors and Attributions

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

Search

Text Color

Text Size

Margin Size

Font Type