4.4E: Exercises for Section 4.4

1) If $c$ is a critical point of $f(x)$, when is there no local maximum or minimum at $c$? Explain.

2) For the function $y=x^3$, is $x=0$ both an inflection point and a local maximum/minimum?

Answer

It is not a local maximum/minimum because $f'$ does not change sign

3) For the function $y=x^3$, is $x=0$ an inflection point?

4) Is it possible for a point $c$ to be both an inflection point and a local extremum of a twice differentiable function?

Answer

No

5) Why do you need continuity for the first derivative test? Come up with an example.

6) Explain whether a concave-down function has to cross $y=0$ for some value of $x$.

Answer

False; for example, $y=\sqrt{x}$.

7) Explain whether a polynomial of degree $2$ can have an inflection point.

In exercises 8 - 12, analyze the graphs of $f'$, then list all intervals where $f$ is increasing or decreasing.

8)

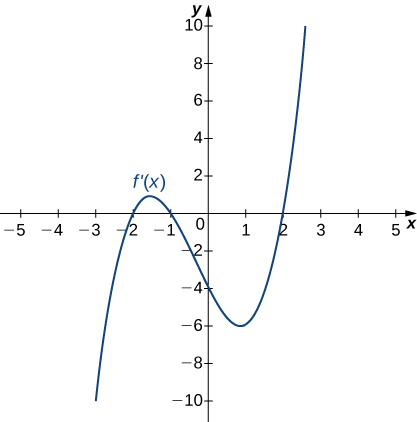
Answer

Increasing for $−2<x<−1$ and $x>2$;
Decreasing for $x<−2$ and $−1<x<2$

9)

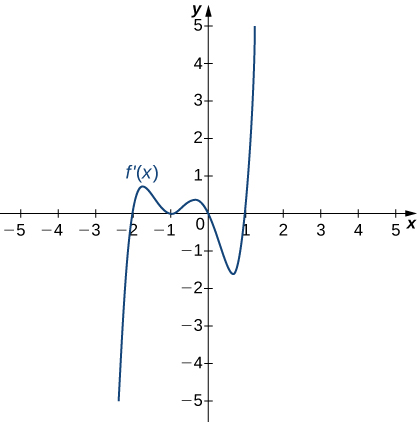
10)

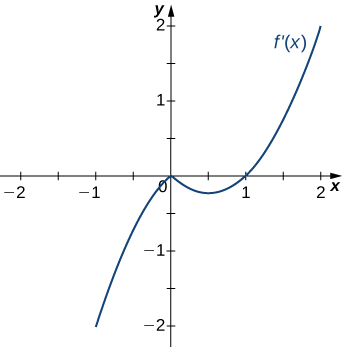
Answer

Decreasing for $x<1$,
Increasing for $x>1$

11)

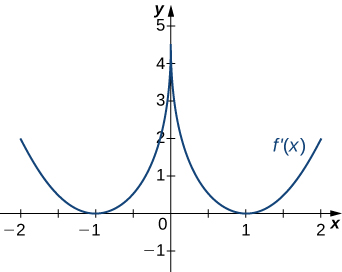
12)

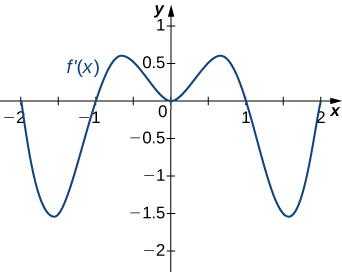
Answer

Decreasing for $−2<x<−1$ and $1<x<2$;
Increasing for $−1<x<1$ and $x<−2$ and $x>2$

In exercises 13 - 17, analyze the graphs of $f'$, then list all intervals where

a. $f$ is increasing and decreasing and

b. the minima and maxima are located.

13)

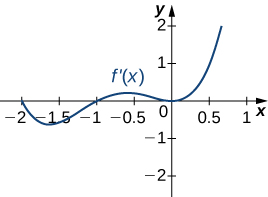
14)

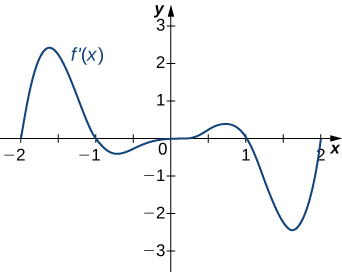
Answer

a. Increasing over $−2<x<−1,\;0<x<1,x>2$, Decreasing over $x<−2, \;−1<x<0, \;1<x<2;$
b. Maxima at $x=−1$ and $x=1$, Minima at $x=−2$ and $x=0$ and $x=2$

15)

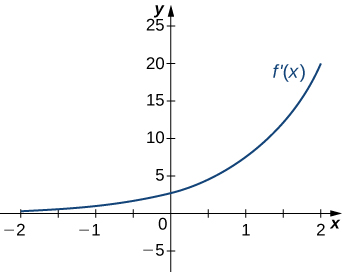
16)

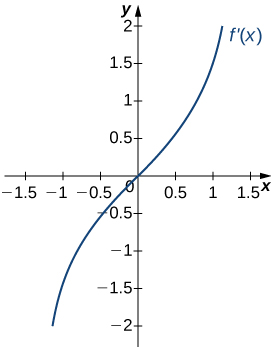
Answer

a. Increasing over $x>0$, Decreasing over $x<0;$
b. Minimum at $x=0$

17)

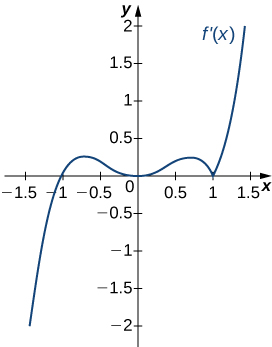
In exercises 18 - 22, analyze the graphs of $f'$, then list all inflection points and intervals $f$ that are concave up and concave down.

18)

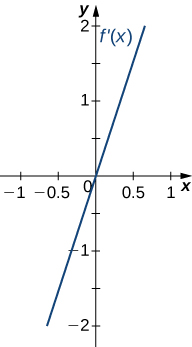
Answer

Concave up for all $x$,
No inflection points

19)

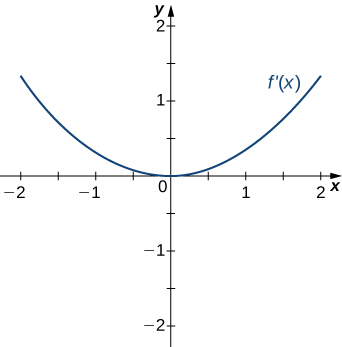
20)

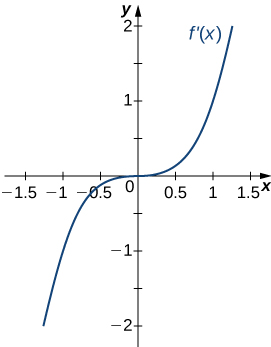
Answer

Concave up for all $x$,
No inflection points

21)

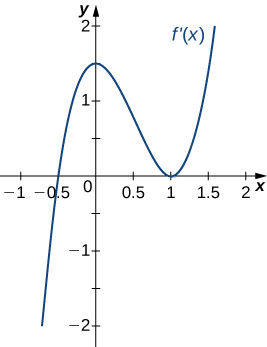
22)

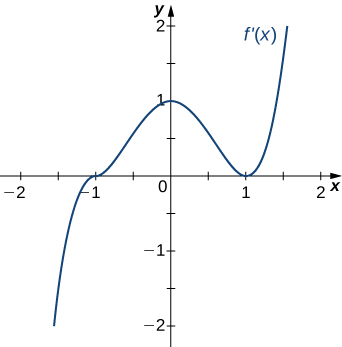
Answer

Concave up for $x<0$ and $x>1$,
Concave down for $0<x<1$,
Inflection points at $x=0$ and $x=1$

For exercises 23 - 27, draw a graph that satisfies the given specifications for the domain $x=[−3,3]$. The function does not have to be continuous or differentiable.

23) $f(x)>0,\;f'(x)>0$ over $x>1,\;−3<x<0,\;f'(x)=0$ over $0<x<1$

24) $f'(x)>0$ over $x>2,\;−3<x<−1,\;f'(x)<0$ over $−1<x<2,\;f''(x)<0$ for all $x$

Answer

Answers will vary

25) $f''(x)<0$ over $−1<x<1,\;f''(x)>0,\;−3<x<−1,\;1<x<3,$ local maximum at $x=0,$ local minima at $x=±2$

26) There is a local maximum at $x=2,$ local minimum at $x=1,$ and the graph is neither concave up nor concave down.

Answer

Answers will vary

27) There are local maxima at $x=±1,$ the function is concave up for all $x$, and the function remains positive for all $x.$

For the following exercises, determine

a. intervals where $f$ is increasing or decreasing and

b. local minima and maxima of $f$.

28) $f(x)=\sin x+\sin^3x$ over $−π<x<π$

Answer

a. Increasing over $−\frac{π}{2}<x<\frac{π}{2},$ decreasing over $x<−\frac{π}{2},\; x>\frac{π}{2}$

b. Local maximum at $x=\frac{π}{2}$; local minimum at $x=−\frac{π}{2}$

29) $f(x)=x^2+\cos x$

For exercise 30, determine

a. intervals where $f$ is concave up or concave down, and

b. the inflection points of $f$.

30) $f(x)=x^3−4x^2+x+2$

Answer

a. Concave up for $x>\frac{4}{3},$ concave down for $x<\frac{4}{3}$

b. Inflection point at $x=\frac{4}{3}$

For exercises 31 - 37, determine

a. intervals where $f$ is increasing or decreasing,

b. local minima and maxima of $f$,

c. intervals where $f$ is concave up and concave down, and

d. the inflection points of $f$.

31) $f(x)=x^2−6x$

32) $f(x)=x^3−6x^2$

Answer

a. Increasing over $x<0$ and $x>4,$ decreasing over $0<x<4$
b. Maximum at $x=0$, minimum at $x=4$
c. Concave up for $x>2$, concave down for $x<2$
d. Inflection point at $x=2$

33) $f(x)=x^4−6x^3$

34) $f(x)=x^{11}−6x^{10}$

Answer

a. Increasing over $x<0$ and $x>\frac{60}{11}$, decreasing over $0<x<\frac{60}{11}$
b. Maximum at $x=0$, minimum at $x=\frac{60}{11}$
c. Concave down for $x<\frac{54}{11}$, concave up for $x>\frac{54}{11}$
d. Inflection point at $x=\frac{54}{11}$

35) $f(x)=x+x^2−x^3$

36) $f(x)=x^2+x+1$

Answer

a. Increasing over $x>−\frac{1}{2}$, decreasing over $x<−\frac{1}{2}$
b. Minimum at $x=−\frac{1}{2}$
c. Concave up for all $x$
d. No inflection points

37) $f(x)=x^3+x^4$

For exercises 38 - 47, determine

a. intervals where $f$ is increasing or decreasing,

b. local minima and maxima of $f$,

c. intervals where $f$ is concave up and concave down, and

d. the inflection points of $f$. Sketch the curve, then use a calculator to compare your answer. If you cannot determine the exact answer analytically, use a calculator.

38) [T] $f(x)=\sin(πx)−\cos(πx)$ over $x=[−1,1]$

Answer

a. Increases over $−\frac{1}{4}<x<\frac{3}{4},$ decreases over $x>\frac{3}{4}$ and $x<−\frac{1}{4}$
b. Minimum at $x=−\frac{1}{4}$, maximum at $x=\frac{3}{4}$
c. Concave up for $−\frac{3}{4}<x<\frac{1}{4}$, concave down for $x<−\frac{3}{4}$ and $x>\frac{1}{4}$
d. Inflection points at $x=−\frac{3}{4},\;x=\frac{1}{4}$

39) [T] $f(x)=x+\sin(2x)$ over $x=[−\frac{π}{2},\frac{π}{2}]$

40) [T] $f(x)=\sin x+\tan x$ over $(−\frac{π}{2},\frac{π}{2})$

Answer

a. Increasing for all $x$
b. No local minimum or maximum
c. Concave up for $x>0$, concave down for $x<0$
d. Inflection point at $x=0$

41) [T] $f(x)=(x−2)^2(x−4)^2$

42) [T] $f(x)=\dfrac{1}{1−x},\quad x≠1$

Answer

a. Increasing for all $x$ where defined
b. No local minima or maxima
c. Concave up for $x<1$; concave down for $x>1$
d. No inflection points in domain

43) [T] $f(x)=\dfrac{\sin x}{x}$ over $x=[-2π,0)∪(0,2π]$

44) $f(x)=\sin(x)e^x$ over $x=[−π,π]$

Answer

a. Increasing over $−\frac{π}{4}<x<\frac{3π}{4}$, decreasing over $x>\frac{3π}{4},\;x<−\frac{π}{4}$
b. Minimum at $x=−\frac{π}{4}$, maximum at $x=\frac{3π}{4}$
c. Concave up for $−\frac{π}{2}<x<\frac{π}{2}$, concave down for $x<−\frac{π}{2},\;x>\frac{π}{2}$
d. Inflection points at $x=±\frac{π}{2}$

45) $f(x)=\ln x\sqrt{x},\quad x>0$

46) $f(x)=\frac{1}{4}\sqrt{x}+\frac{1}{x},\quad x>0$

Answer

a. Increasing over $x>4,$ decreasing over $0<x<4$
b. Minimum at $x=4$
c. Concave up for $0<x<8\sqrt[3]{2}$, concave down for $x>8\sqrt[3]{2}$
d. Inflection point at $x=8\sqrt[3]{2}$

47) $f(x)=\dfrac{e^x}{x},\quad x≠0$

In exercises 48 - 52, interpret the sentences in terms of $f$, $f'$, and $f''$.

48) The population is growing more slowly. Here $f$ is the population.

Answer

$f>0,\;f'>0,\;f''<0$

49) A bike accelerates faster, but a car goes faster. Here $f=$ Bike’s position minus Car’s position.

50) The airplane lands smoothly. Here $f$ is the plane’s altitude.

Answer

$f>0,\;f'<0,\;f''>0$

51) Stock prices are at their peak. Here $f$is the stock price.

52) The economy is picking up speed. Here $f$ is a measure of the economy, such as GDP.

Answer

$f>0,\;f'>0,\;f''>0$

For exercises 53 - 57, consider a third-degree polynomial $f(x)$, which has the properties $f'(1)=0$ and $f'(3)=0$.

Determine whether the following statements are true or false. Justify your answer.

53) $f(x)=0$ for some $1≤x≤3$.

54) $f''(x)=0$ for some $1≤x≤3$.

Answer

True, by the Mean Value Theorem

55) There is no absolute maximum at $x=3$.

56) If $f(x)$ has three roots, then it has $1$ inflection point.

Answer

True, examine derivative

57) If $f(x)$ has one inflection point, then it has three real roots.