Derivatives of the Inverse Trigonometric Functions

Last updated
Save as PDF

Page ID: 17554

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Determining the Derivatives of the Inverse Trigonometric Functions

Now let's determine the derivatives of the inverse trigonometric functions, $y = \arcsin x,$ $y = \arccos x,$ $y = \arctan x,$ $ y = \text{arccot}\, x,$ $y = \text{arcsec}\, x,$ and $y = \text{arccsc}\, x.$

One way to do this that is particularly helpful in understanding how these derivatives are obtained is to use a combination of implicit differentiation and right triangles. An added benefit of this approach is that it will prepare you to be more successful in a future topic called trigonometric substitution.

Example $\PageIndex{1}$: Finding the derivative of $y = \arcsin x$

Find the derivative of $y = \arcsin x$.

Solution:

To find the derivative of $y = \arcsin x$, we will first rewrite this equation in terms of its inverse form. That is, \[ \sin y = x \label{inverseEqSine}\]

Now this equation shows that $y$ can be considered an acute angle in a right triangle with a sine ratio of $\dfrac{x}{1}$. Since the sine ratio gives us the length of the opposite side over the length of the hypotenuse, this means that the opposite side has a length of $x$ and the hypotenuse has a length of $1$. See Figure $\PageIndex{1}$.

$inverseTrigSineRtTri1a.png$
Figure $\PageIndex{1}$

Now let's differentiate Equation \ref{inverseEqSine} implicitly with respect to $x$.

\[\cos y \cdot \frac{dy}{dx} = 1\]

Then we solve this for $\dfrac{dy}{dx}$.

\[\frac{dy}{dx} =\frac{1}{\cos y}\]

Looking at Figure $\PageIndex{1}$, we see that $\cos y = a$. Now we use the Pythagorean Theorem to find an expression for $a$ in terms of $x$ using the other sides of the right triangle that we know.

Thus we have:

\[\begin{align*} a^2 + x^2 &= 1^2 \\[5pt]
a^2 &= 1 - x^2 \\[5pt]
a &= \sqrt{1-x^2} \end{align*}\]

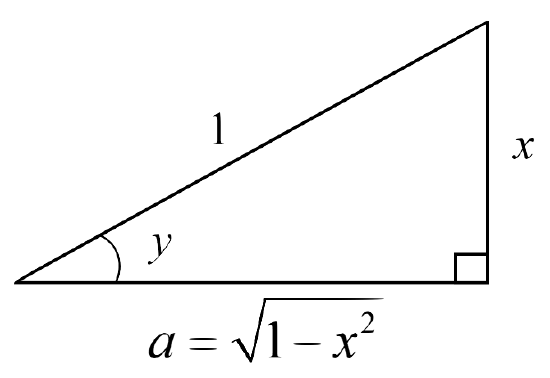
$inverseTrigSineRtTri1b.png$
Figure $\PageIndex{2}$

Now using this result, we see that \[\cos y = \sqrt{1-x^2} \]

\[\frac{dy}{dx} =\frac{1}{\cos y} = \frac{1}{\sqrt{1-x^2}}\]

Thus we have found the derivative of $ y = \arcsin x$,

\[\frac{d}{dx}\big( \arcsin x \big) = \frac{1}{\sqrt{1-x^2}}\]

Exercise $\PageIndex{1}$

Use the same approach to determine the derivatives of $y = \arccos x,$ $y = \arctan x,$ and $y = \text{arccot} \,x.$

Answer: \[\begin{align*} \frac{d}{dx}\big( \arccos x \big) &= \frac{-1}{\sqrt{1-x^2}} \\[5pt]
\frac{d}{dx}\big( \arctan x \big) &= \frac{1}{1+x^2} \\[5pt]
\frac{d}{dx}\big( \text{arccot} \,x \big) &= \frac{-1}{1+x^2} \end{align*} \]

Example $\PageIndex{2}$: Finding the derivative of $y = \text{arcsec}\, x$

Find the derivative of $y = \text{arcsec}\, x$.

Solution:

To find the derivative of $y = \text{arcsec}\, x$, we will first rewrite this equation in terms of its inverse form. That is, \[ \sec y = x \label{inverseEqSec}\]

As before, let $y$ be considered an acute angle in a right triangle with a secant ratio of $\dfrac{x}{1}$. Since the secant ratio is the reciprocal of the cosine ratio, it gives us the length of the hypotenuse over the length of the adjacent side, so this means that the hypotenuse has a length of $x$ and the adjacent side has a length of $1$. See Figure $\PageIndex{3}$.

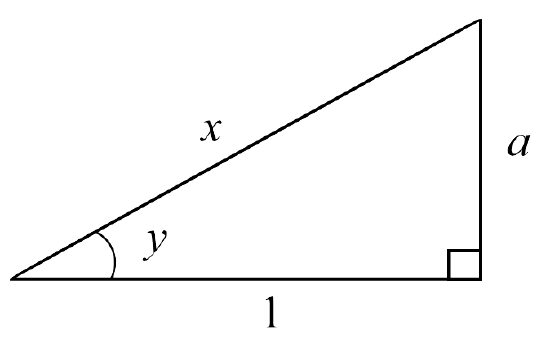
$inverseTrigSecRtTri1a.png$
Figure $\PageIndex{3}$

Differentiating Equation \ref{inverseEqSec} implicitly with respect to $x$, gives us:

\[\sec y\tan y \cdot \frac{dy}{dx} = 1\]

Solving this for $\dfrac{dy}{dx}$, we get:

\[\frac{dy}{dx} =\frac{1}{\sec y\tan y}\]

In order to find $\tan y$ in terms of $x$, we need to find the length of the opposite side, $a$, in terms of $x$. By the Pythagorean Theorem, we have:

\[\begin{align*} 1^2 + a^2 &= x^2 \\[5pt]
a^2 &= x^2 - 1 \\[5pt]
a &= \sqrt{x^2-1} \end{align*}\]

Figure $\PageIndex{4}$ shows the resulting right triangle.

$inverseTrigSecRtTri1b.png$
Figure $\PageIndex{4}$

From the right triangle in Figure $\PageIndex{4}$, we can see that \[\tan y = \sqrt{x^2 - 1}.\]

Since $\sec y = x$, it appears that

\[\frac{dy}{dx} =\frac{1}{\sec y\tan y} = \frac{1}{x\sqrt{x^2 - 1}}.\]

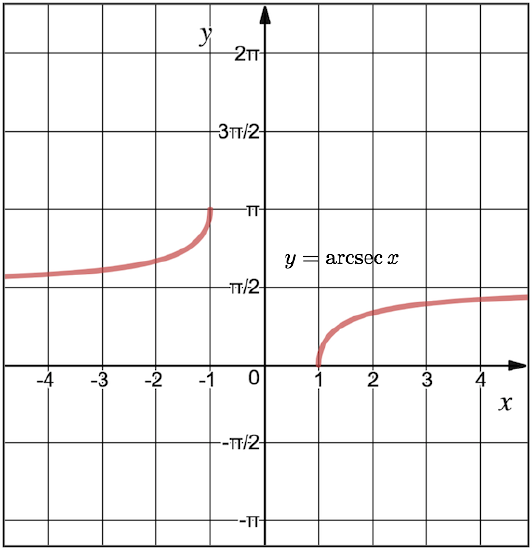
But this is not completely correct, at least not for negative values of $x$. Considering the graph of $y = \text{arcsec}\, x$ in Figure $\PageIndex{5}$, we see that its slope is always positive. But for negative values of $x$, the form of the derivative stated above would be negative (and clearly incorrect).

$arcsecx2.png$
Figure $\PageIndex{5}$

As we'll prove below, the actual derivative formula for this function is:

\[\frac{d}{dx}\big( \text{arcsec}\, x \big) = \frac{1}{|x|\sqrt{x^2 - 1}}\]

Consider the domain and range of the original function, $y = \text{arcsec}\, x:$

\[\text{Domain: } (-\infty, -1] \cup [1, \infty) \quad \text{or} \quad |x| \geq 1\]
\[\text{Range: } \big[0, \frac{\pi}{2}\big) \cup \big(\frac{\pi}{2}, \pi\big] \quad \text{or} \quad 0 \leq y \leq \pi, y \ne \frac{\pi}{2}\]

Note that the domain of the derivative is a subset of the domain of the original function, excluding the endpoints, $x = -1$ and $x = 1.$

Now, let's rewrite $\dfrac{dy}{dx}$ as:

\[\frac{dy}{dx} =\frac{1}{\sec y\tan y} = \frac{\cos y}{1}\cdot\frac{\cos y}{\sin y} = \frac{\cos^2 y}{\sin y}\]

We see that this function allows $y$ to have all values between $0$ and $\pi$, except for $y = \frac{\pi}{2}$, where the original expression $\dfrac{1}{\sec y\tan y}$ is undefined. This is a subset of the range of the original function $y = \text{arcsec}\, x.$ Note that in the derivative, $y$ cannot take on the values of the endpoints of this interval, while these were part of the range of $y = \text{arcsec}\, x.$

Now consider that for all values of $y$ in this range between $0$ and $\pi$, the expression for $\dfrac{dy}{dx}$ is positive, as both

$\sin y \gt 0$ and $\cos^2 y \gt 0$ for all $y \in (0, \pi)$.

Therefore, we have that,

\[\frac{d}{dx}\big( \text{arcsec}\, x \big) = \frac{1}{|x|\sqrt{x^2 - 1}}.\]

Exercise $\PageIndex{2}$

Use the same approach to determine the derivative of $y = \text{arccsc} \,x.$

Answer: \[\frac{d}{dx}\big( \text{arccsc}\, x \big) = \frac{-1}{|x|\sqrt{x^2 - 1}}.\nonumber\]

Using the Chain Rule with Inverse Trigonometric Functions

Now let's see how to use the chain rule to find the derivatives of inverse trigonometric functions with more interesting functional arguments.

Example $\PageIndex{3}$:

Find the derivatives for each of the following functions:

$\quad y = \arcsin(x^2) $
$\quad y = \arctan(x^3+1) $
$\quad y = \text{arcsec}(\ln|x|) $
$\quad y = \arcsin(\cos x) $

Solution:

Using the chain rule, we see that: \[ \frac{d}{dx}\big(\arcsin(x^2) \big) = \frac{1}{\sqrt{1-(x^2)^2}}\cdot \frac{d}{dx}\big(x^2\big) = \frac{2x}{\sqrt{1-x^4}}\]
Here we have: \[ \frac{d}{dx}\big(\arctan(x^3+1) \big) = \frac{1}{1+(x^3+1)^2}\cdot \frac{d}{dx}\big(x^3+1\big) = \frac{3x^2}{1+(x^3+1)^2}\]
Although it would likely be fine as it is, we can simplify it to obtain: \[ \frac{d}{dx}\big(\arctan(x^3+1) \big) = \frac{3x^2}{x^6+2x^3+2}\]
For $ y = \text{arcsec}(\ln|x|) $, we obtain: \[ \frac{d}{dx}\big(\text{arcsec}(\ln|x|)\big) = \frac{1}{|\ln|x||\sqrt{(\ln|x|)^2 - 1}}\cdot \frac{d}{dx}\big(\ln|x|\big) = \frac{1}{x |\ln|x||\sqrt{(\ln|x|)^2 - 1}}\]
For $ y = \arcsin(\cos x)$, we obtain: \[ \frac{d}{dx}\big(\arcsin(\cos x) \big) = \frac{1}{\sqrt{1-(\cos x)^2}}\cdot \frac{d}{dx}\big(\cos x\big) = \frac{-\sin x}{\sqrt{\sin^2 x}}\]
Note that it may look like the denominator should simplify to $\sin x$ and the entire derivative to $\frac{dy}{dx} = -1$. But this is not the case. Remember that
\[ \sqrt{x^2} = |x|.\]
This means that what we actually obtain here is something more interesting: \[ \frac{d}{dx}\big(\arcsin(\cos x) \big) = \frac{-\sin x}{|\sin x|}\]
This function alternates between values of $-1$ and $1$, when $\sin x$ is positive and negative, respectively.
See the graph of the function $ y = \arcsin(\cos x)$ below in Figure $\PageIndex{6}$.

$plotArcsin(cosx).png$
Figure $\PageIndex{6}$: Graph of $ y = \arcsin(\cos x)$.

Derivative Formulas

In the same way that we can encapsulate the chain rule in the derivative of $\ln u$ as $\dfrac{d}{dx}\big(\ln u\big) = \dfrac{u'}{u}$, we can write formulas for the derivative of the inverse trigonometric functions that encapsulate the chain rule. Note that $u$ represents a function of $x$ in these formulas, and $u'$ represents the derivative of $u$ with respect to $x$.

\[\begin{align*} \frac{d}{dx}\big(\arcsin u\big) \quad&=\quad \frac{u'}{\sqrt{1-u^2}} & &\frac{d}{dx}\big(\arccos u\big) \quad=\quad \frac{-u'}{\sqrt{1-u^2}} \\
\frac{d}{dx}\big(\arctan u\big) \quad&=\quad \frac{u'}{1+u^2} & & \frac{d}{dx}\big(\text{arccot}\, u\big) \quad=\quad \frac{-u'}{1+u^2} \\
\frac{d}{dx}\big(\text{arcsec}\, u\big) \quad&=\quad \frac{u'}{|u|\sqrt{u^2-1}} & & \frac{d}{dx}\big(\text{arccsc}\, u\big) \quad=\quad \frac{-u'}{|u|\sqrt{u^2-1}} \end{align*} \]

Contributors

Paul Seeburger (Monroe Community College)