8.3E: Exercises for Separable Differential Equations
- Last updated
- Jun 30, 2021
- Save as PDF
- Page ID
- 18484
( \newcommand{\kernel}{\mathrm{null}\,}\)
In exercises 1 - 4, solve the following initial-value problems with the initial condition y0=0 and graph the solution.
1) dydt=y+1
- Answer
- y=et−1
2) dydt=y−1
3) dydt=−y+1
- Answer
- y=1−e−t
4) dydt=−y−1
In exercises 5 - 14, find the general solution to the differential equation.
5) x2y′=(x+1)y
- Answer
- y=Cxe−1/x
6) y′=tan(y)x
7) y′=2xy2
- Answer
- y=1C−x2
8) dydt=ycos(3t+2)
9) 2xdydx=y2
- Answer
- y=−2C+ln|x|
10) y′=eyx2
11) (1+x)y′=(x+2)(y−1)
- Answer
- y=Cex(x+1)+1
12) dxdt=3t2(x2+4)
13) tdydt=√1−y2
- Answer
- y=sin(ln|t|+C)
14) y′=exey
In exercises 15 - 24, find the solution to the initial-value problem.
15) y′=ey−x,y(0)=0
- Answer
- y=−ln(e−x) which simplifies to y=x
16) y′=y2(x+1),y(0)=2
17) dydx=y3xex2,y(0)=1
- Answer
- y=1√2−ex2
18) dydt=y2exsin(3x),y(0)=1
19) y′=xsech2y,y(0)=0
- Answer
- y=tanh−1(x22)
20) y′=2xy(1+2y),y(0)=−1
21) dxdt=ln(t)√1−x2,x(1)=0
- Answer
- x=sin(1−t+tlnt)
22) y′=3x2(y2+4),y(0)=0
23) y′=ey5x,y(0)=ln(ln(5))
- Answer
- y=ln(ln(5))−ln(2−5x)
24) y′=−2xtan(y),y(0)=π2
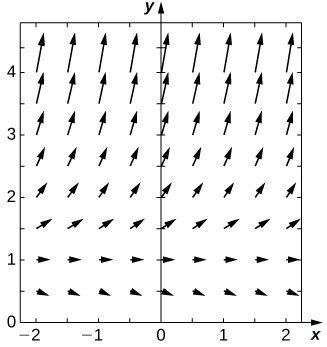
For problems 25 - 29, use a software program or your calculator to generate the directional fields. Solve explicitly and draw solution curves for several initial conditions. Are there some critical initial conditions that change the behavior of the solution?
25) [T] y′=1−2y
- Answer
-
y=Ce−2x+12
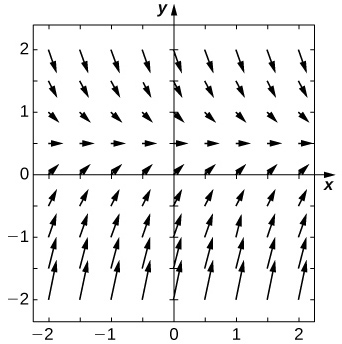
26) [T] y′=y2x3
27) [T] y′=y3ex
- Answer
-
y=1√2√C−ex
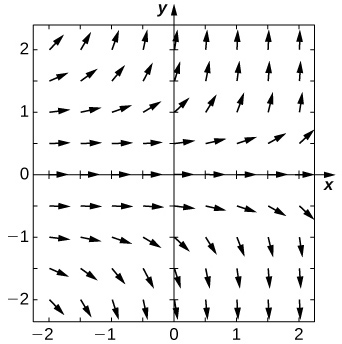
28) [T] y′=ey
29) [T] y′=yln(x)
- Answer
-
y=Ce−xxx
30) Most drugs in the bloodstream decay according to the equation y′=cy, where y is the concentration of the drug in the bloodstream. If the half-life of a drug is 2 hours, what fraction of the initial dose remains after 6 hours?
31) A drug is administered intravenously to a patient at a rate r mg/h and is cleared from the body at a rate proportional to the amount of drug still present in the body, d. Set up and solve the differential equation, assuming there is no drug initially present in the body.
- Answer
- y=rd(1−e−dt)
32) [T] How often should a drug be taken if its dose is 3 mg, it is cleared at a rate c=0.1 mg/h, and 1 mg is required to be in the bloodstream at all times?
33) A tank contains 1 kilogram of salt dissolved in 100 liters of water. A salt solution of 0.1 kg salt/L is pumped into the tank at a rate of 2 L/min and is drained at the same rate. Solve for the salt concentration at time t. Assume the tank is well mixed.
- Answer
- Since the amount of salt at time t is given by the equation A(t)=10−9e−t/50, and the tank volume stays constant at 100 liters, the concentration at time t would be c(t)=1100(10−9e−t/50).
34) A tank containing 10 kilograms of salt dissolved in 1000 liters of water has two salt solutions pumped in. The first solution of 0.2 kg salt/L is pumped in at a rate of 20 L/min and the second solution of 0.05 kg salt/L is pumped in at a rate of 5 L/min. The tank drains at 25 L/min. Assume the tank is well mixed. Solve for the salt concentration at time t.
35) [T] For the preceding problem, find how much salt is in the tank 1 hour after the process begins.
- Answer
- 134.3 kilograms
36) Torricelli’s law states that for a water tank with a hole in the bottom that has a cross-section of A and with a height of water h above the bottom of the tank, the rate of change of volume of water flowing from the tank is proportional to the square root of the height of water, according to dVdt=−A√2gh, where g is the acceleration due to gravity. Note that dVdt=Adhdt. Solve the resulting initial-value problem for the height of the water, assuming a tank with a hole of radius 2 ft. The initial height of water is 100 ft.
37) For the preceding problem, determine how long it takes the tank to drain.
- Answer
- 720 seconds
For problems 38 - 44, use Newton’s law of cooling.
38) The liquid base of an ice cream has an initial temperature of 200°F before it is placed in a freezer with a constant temperature of 0°F. After 1 hour, the temperature of the ice-cream base has decreased to 140°F. Formulate and solve the initial-value problem to determine the temperature of the ice cream.
39) [T] The liquid base of an ice cream has an initial temperature of 210°F before it is placed in a freezer with a constant temperature of 20°F. After 2 hours, the temperature of the ice-cream base has decreased to 170°F. At what time will the ice cream be ready to eat? (Assume 30°F is the optimal eating temperature.)
- Answer
- 24 hours 55 minutes
40) [T] You are organizing an ice cream social. The outside temperature is 80°F and the ice cream is at 10°F. After 10 minutes, the ice cream temperature has risen by 10°F. How much longer can you wait before the ice cream melts at 40°F?
41) You have a cup of coffee at temperature 70°C and the ambient temperature in the room is 20°C. Assuming a cooling rate k of 0.125, write and solve the differential equation to describe the temperature of the coffee with respect to time.
- Answer
- T(t)=20+50e^{−0.125t}
42) [T] You have a cup of coffee at temperature 70°C that you put outside, where the ambient temperature is 0°C. After 5 minutes, how much colder is the coffee?
43) You have a cup of coffee at temperature 70°C and you immediately pour in 1 part milk to 5 parts coffee. The milk is initially at temperature 1°C. Write and solve the differential equation that governs the temperature of this coffee.
- Answer
- T(t)=20+38.5e^{−0.125t}
44) You have a cup of coffee at temperature 70°C, which you let cool 10 minutes before you pour in the same amount of milk at 1°C as in the preceding problem. How does the temperature compare to the previous cup after 10 minutes?
45) Solve the generic problem y'=ay+b with initial condition y(0)=c.
- Answer
- y=(c+ba)e^{ax}−\frac{b}{a}
46) Prove the basic continual compounded interest equation. Assuming an initial deposit of P_0 and an interest rate of r, set up and solve an equation for continually compounded interest.
47) Assume an initial nutrient amount of I kilograms in a tank with L liters. Assume a concentration of c kg/L being pumped in at a rate of r L/min. The tank is well mixed and is drained at a rate of r L/min. Find the equation describing the amount of nutrient in the tank.
- Answer
- y(t)=cL+(I−cL)e^{−rt/L}
48) Leaves accumulate on the forest floor at a rate of 2 g/cm2/yr and also decompose at a rate of 90 \% per year. Write a differential equation governing the number of grams of leaf litter per square centimeter of forest floor, assuming at time 0 there is no leaf litter on the ground. Does this amount approach a steady value? What is that value?
49) Leaves accumulate on the forest floor at a rate of 4 g/cm2/yr. These leaves decompose at a rate of 10 \% per year. Write a differential equation governing the number of grams of leaf litter per square centimeter of forest floor. Does this amount approach a steady value? What is that value?
- Answer
- Differential Equation: \dfrac{dy}{dt} = 4 - 0.1y
Solution, the model for this situation: y=40(1−e^{−0.1t}),
Amount approaches a steady value of 40 g/cm2


