Evaluating Polar Double Integrals
In exercises 16 - 25, evaluate the double integral \(\displaystyle \iint_R f(x,y) \,dA\) over the polar rectangular region \(R\).
16) \(f(x,y) = x^2 + y^2\), \(R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}\)
17) \(f(x,y) = x + y\), \(R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}\)
- Answer
- \(0\)
18) \(f(x,y) = x^2 + xy, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \pi \leq \theta \leq 2\pi\big\}\)
19) \(f(x,y) = x^4 + y^4, \space R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{3\pi}{2} \leq \theta \leq 2\pi\big\}\)
- Answer
- \(\frac{63\pi}{16}\)
20) \(f(x,y) = \sqrt[3]{x^2 + y^2}\), where \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}\).
21) \(f(x,y) = x^4 + 2x^2y^2 + y^4\), where \(R = \big\{(r,\theta)\,|\,3 \leq r \leq 4, \space \frac{\pi}{3} \leq \theta \leq \frac{2\pi}{3}\big\}\).
- Answer
- \(\frac{3367\pi}{18}\)
22) \(f(x,y) = \sin (\arctan \frac{y}{x})\), where \(R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}\)
23) \(f(x,y) = \arctan \left(\frac{y}{x}\right)\), where \(R = \big\{(r, \theta)\,|\,2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\)
- Answer
- \(\frac{35\pi^2}{576}\)
24) \(\displaystyle \iint_R e^{x^2+y^2} \left[1 + 2 \space \arctan \left(\frac{y}{x}\right)\right] \,dA, \space R = \big\{(r,\theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \frac{\pi}{3}\big\}\)
25) \(\displaystyle \iint_R \left(e^{x^2+y^2} + x^4 + 2x^2y^2 + y^4 \right) \arctan \left(\frac{y}{x}\right) \,dA, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\)
- Answer
- \(\frac{7}{576}\pi^2 (21 - e + e^4)\)
In exercises 26 - 29, the integrals have been converted to polar coordinates. Verify that the identities are true and choose the easiest way to evaluate the integrals, in rectangular or polar coordinates.
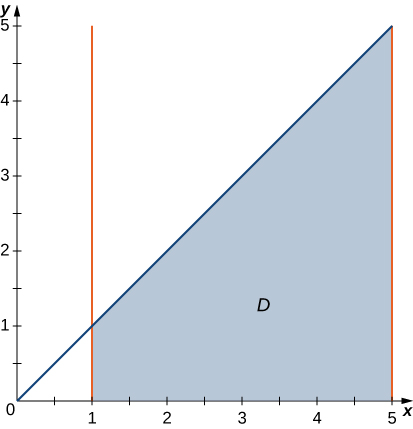
26) \(\displaystyle \int_1^2 \int_0^x (x^2 + y^2)\,dy \space dx = \int_0^{\frac{\pi}{4}} \int_{\sec \theta}^{2 \space \sec \theta}r^3 \,dr \space d\theta\)
27) \(\displaystyle \int_2^3 \int_0^x \frac{x}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \int_{2\sec\theta}^{3\sec \theta} \,r \space \cos \theta \space dr \space d\theta\)
- Answer
- \(\frac{5}{2} \ln (1 + \sqrt{2})\)
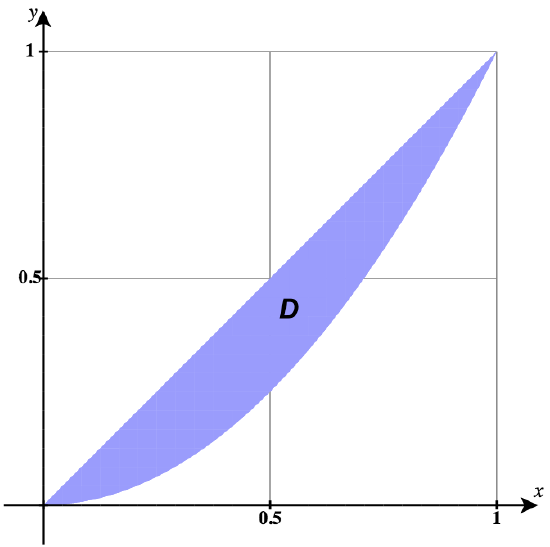
28) \(\displaystyle \int_0^1 \int_{x^2}^x \frac{1}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \space dr \space d\theta\)
29) \(\displaystyle \int_0^1 \int_{x^2}^x \frac{y}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \,r \space \sin \theta \space dr \space d\theta\)
- Answer
- \(\frac{1}{6}(2 - \sqrt{2})\)
In exercises 30 - 37, draw the region of integration, \(R\), labeling all limits of integration, convert the integrals to polar coordinates and evaluate them.
30) \(\displaystyle \int_0^3 \int_0^{\sqrt{9-y^2}}\left(x^2 + y^2\right)\,dx \space dy\)
31) \(\displaystyle \int_0^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}}\left(x^2 + y^2\right)^2\,dx \space dy\)
- Answer
- \(\displaystyle \int_0^{\pi} \int_0^2 r^5 \,dr \space d\theta \quad = \quad \frac{32\pi}{3}\)
32) \(\displaystyle \int_0^1 \int_0^{\sqrt{1-x^2}} (x + y) \space dy \space dx\)
33) \(\displaystyle \int_0^4 \int_{-\sqrt{16-x^2}}^{\sqrt{16-x^2}} \sin (x^2 + y^2) \space dy \space dx\)
- Answer
- \(\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^4 \,r \space \sin (r^2) \space dr \space d\theta \quad = \quad \pi \space \sin^2 8\)
34) \(\displaystyle \int_0^5 \int_{-\sqrt{25-x^2}}^{\sqrt{25-x^2}}\sqrt{x^2+y^2}\,dy\,dx\)
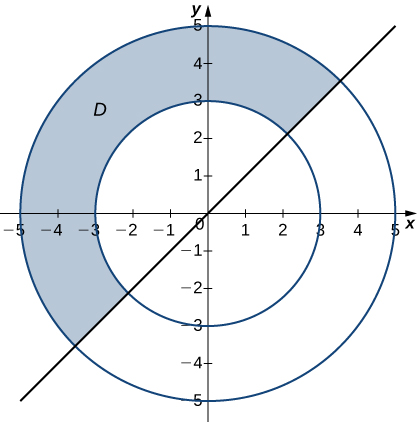
35) \(\displaystyle \int_{-4}^4 \int_{-\sqrt{16-y^2}}^{0}(2y-x)\,dx\,dy\)
- Answer
- \(\displaystyle \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} \int_0^{4} \big( 2r\sin \theta - r\cos\theta\big) \,r\,dr \space d\theta \quad = \quad \frac{128}{3}\)
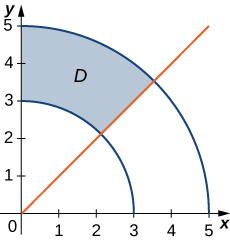
36) \(\displaystyle \int_0^2 \int_{y}^{\sqrt{8-y^2}}(x+y)\,dx\,dy\)
37) \(\displaystyle \int_{-2}^{-1} \int_{0}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_{-1}^1\int_{\sqrt{1-x^2}}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_1^2\int_0^{\sqrt{4-x^2}}(x+5)\,dy\,dx\)
- Answer
- \(\displaystyle \int_{0}^{\pi} \int_1^{2} \big( r\cos \theta + 5\big) \,r\,dr \space d\theta \quad = \quad \frac{15\pi}{2}\)
38) Evaluate the integral \(\displaystyle \iint_D r \,dA\) where \(D\) is the region bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \theta\).
39) Find the area of the region \(D\) bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \theta\).
- Answer
- \(\frac{3\pi}{4}\)
40) Evaluate the integral \(\displaystyle \iint_D r \,dA,\) where \(D\) is the region bounded by the part of the four-leaved rose \(r = \sin 2\theta\) situated in the first quadrant (see the following figure).
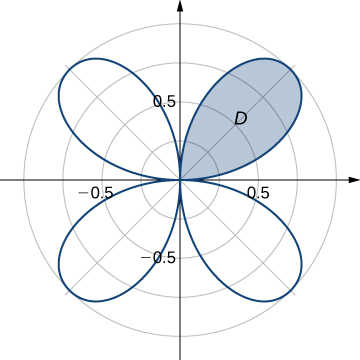
41) Find the total area of the region enclosed by the four-leaved rose \(r = \sin 2\theta\) (see the figure in the previous exercise).
- Answer
- \(\frac{\pi}{2}\)
42) Find the area of the region \(D\) which is the region bounded by \(y = \sqrt{4 - x^2}\), \(x = \sqrt{3}\), \(x = 2\), and \(y = 0\).
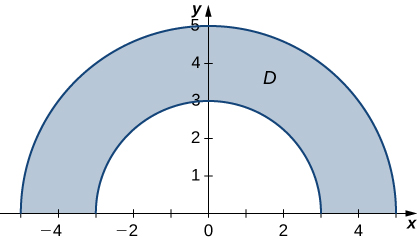
43) Find the area of the region \(D\), which is the region inside the disk \(x^2 + y^2 \leq 4\) and to the right of the line \(x = 1\).
- Answer
- \(\frac{1}{3}(4\pi - 3\sqrt{3})\)
44) Determine the average value of the function \(f(x,y) = x^2 + y^2\) over the region \(D\) bounded by the polar curve \(r = \cos 2\theta\), where \(-\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4}\) (see the following graph).
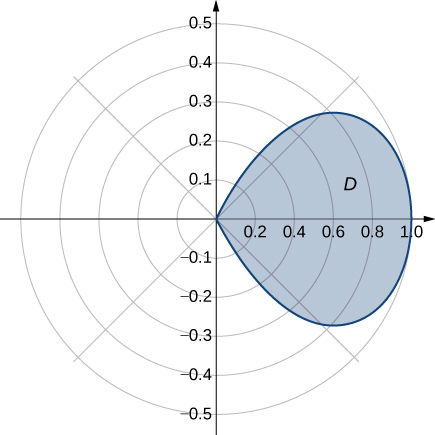
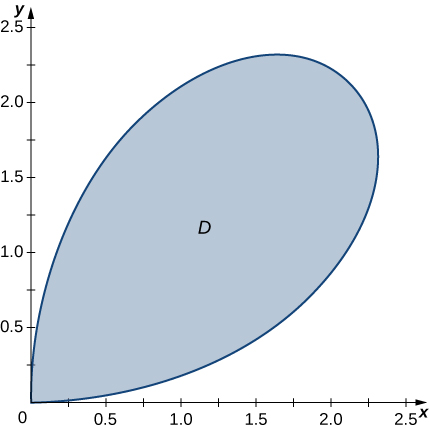
45) Determine the average value of the function \(f(x,y) = \sqrt{x^2 + y^2}\) over the region \(D\) bounded by the polar curve \(r = 3\sin 2\theta\), where \(0 \leq \theta \leq \frac{\pi}{2}\) (see the following graph).
- Answer
- \(\frac{16}{3\pi}\)
46) Find the volume of the solid situated in the first octant and bounded by the paraboloid \(z = 1 - 4x^2 - 4y^2\) and the planes \(x = 0, \space y = 0\), and \(z = 0\).
47) Find the volume of the solid bounded by the paraboloid \(z = 2 - 9x^2 - 9y^2\) and the plane \(z = 1\).
- Answer
- \(\frac{\pi}{18}\)
48)
- Find the volume of the solid \(S_1\) bounded by the cylinder \(x^2 + y^2 = 1\) and the planes \(z = 0\) and \(z = 1\).
- Find the volume of the solid \(S_2\) outside the double cone \(z^2 = x^2 + y^2\) inside the cylinder \(x^2 + y^2 = 1\), and above the plane \(z = 0\).
- Find the volume of the solid inside the cone \(z^2 = x^2 + y^2\) and below the plane \(z = 1\) by subtracting the volumes of the solids \(S_1\) and \(S_2\).
49)
- Find the volume of the solid \(S_1\) inside the unit sphere \(x^2 + y^2 + z^2 = 1\) and above the plane \(z = 0\).
- Find the volume of the solid \(S_2\) inside the double cone \((z - 1)^2 = x^2 + y^2\) and above the plane \(z = 0\).
- Find the volume of the solid outside the double cone \((z - 1)^2 = x^2 + y^2\) and inside the sphere \(x^2 + y^2 + z^2 = 1\).
- Answer
- a. \(\frac{2\pi}{3}\); b. \(\frac{\pi}{2}\); c. \(\frac{\pi}{6}\)
In Exercises 50-51, special double integrals are presented that are especially well suited for evaluation in polar coordinates.
50) The surface of a right circular cone with height \(h\) and base radius \(a\) can be described by the equation \(f(x,y)=h-h\sqrt{\frac{x^2}{a^2}+\frac{y^2}{a^2}}\), where the tip of the cone lies at \((0,0,h)\) and the circular base lies in the \(xy\)-plane, centered at the origin.
Confirm that the volume of a right circular cone with height \(h\) and base radius \(a\) is \(V=\frac{1}{3}\pi a^2h\) by evaluating \(\displaystyle \int\int_R f(x,y)\,dA\) in polar coordinates.
51) Consider \(\displaystyle \int\int_R e^{-(x^2+y^2)}\,dA.\)
(a) Why is this integral difficult to evaluate in rectangular coordinates, regardless of the region \(R\)?
(b) Let \(R\) be the region bounded by the circle of radius \(a\) centered at the origin. Evaluate the double integral using polar coordinates.
(c) Take the limit of your answer from (b), as \(a\to \infty\). What does this imply about the volume under the surface of \(e^{-(x^2+y^2)}\) over the entire \(xy\)-plane?
For the following two exercises, consider a spherical ring, which is a sphere with a cylindrical hole cut so that the axis of the cylinder passes through the center of the sphere (see the following figure).

52) If the sphere has radius 4 and the cylinder has radius 2 find the volume of the spherical ring.
53) A cylindrical hole of diameter 6 cm is bored through a sphere of radius 5 cm such that the axis of the cylinder passes through the center of the sphere. Find the volume of the resulting spherical ring.
- Answer
- \(\frac{256\pi}{3} \space \text{cm}^3\)
54) Find the volume of the solid that lies under the double cone \(z^2 = 4x^2 + 4y^2\), inside the cylinder \(x^2 + y^2 = x\), and above the plane \(z = 0\).
55) Find the volume of the solid that lies under the paraboloid \(z = x^2 + y^2\), inside the cylinder \(x^2 + y^2 = 1\) and above the plane \(z = 0\).
- Answer
- \(\frac{3\pi}{32}\)
56) Find the volume of the solid that lies under the plane \(x + y + z = 10\) and above the disk \(x^2 + y^2 = 4x\).
57) Find the volume of the solid that lies under the plane \(2x + y + 2z = 8\) and above the unit disk \(x^2 + y^2 = 1\).
- Answer
- \(4\pi\)
58) A radial function \(f\) is a function whose value at each point depends only on the distance between that point and the origin of the system of coordinates; that is, \(f (x,y) = g(r)\), where \(r = \sqrt{x^2 + y^2}\). Show that if \(f\) is a continuous radial function, then
\[\iint_D f(x,y)dA = (\theta_2 - \theta_1) [G(R_2) - G(R_1)], \space where \space G'(r) = rg(r) \nonumber \] and \((x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}\), with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\).
59) Use the information from the preceding exercise to calculate the integral \(\displaystyle \iint_D (x^2 + y^2)^3 dA,\) where \(D\) is the unit disk.
- Answer
- \(\frac{\pi}{4}\)
60) Let \(f(x,y) = \dfrac{F'(r)}{r}\) be a continuous radial function defined on the annular region \(D = \big\{(r,\theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}\), where \(r = \sqrt{x^2 + y^2}\), \(0 < R_1 < R_2\), and \(F\) is a differentiable function.
Show that \(\displaystyle \iint_D f(x,y)\,dA = 2\pi [F(R_2) - F(R_1)].\)
61) Apply the preceding exercise to calculate the integral \(\displaystyle \iint_D \frac{e^{\sqrt{x^2+y^2}}}{\sqrt{x^2 + y^2}} \,dx \space dy\) where \(D\) is the annular region between the circles of radii 1 and 2 situated in the third quadrant.
- Answer
- \(\frac{1}{2} \pi e(e - 1)\)
62) Let \(f\) be a continuous function that can be expressed in polar coordinates as a function of \(\theta\) only; that is, \(f(x,y) = h(\theta)\), where \((x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}\), with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\).
Show that \(\displaystyle \iint_D f(x,y) \,dA = \frac{1}{2} (R_2^2 - R_1^2) [H(\theta_2) - H(\theta_1)]\), where \(H\) is an antiderivative of \(h\).
63) Apply the preceding exercise to calculate the integral \(\displaystyle \iint_D \frac{y^2}{x^2}\,dA,\) where \(D = \big\{(r, \theta)\,|\, 1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}.\)
- Answer
- \(\sqrt{3} - \frac{\pi}{4}\)
64) Let \(f\) be a continuous function that can be expressed in polar coordinates as a function of \(\theta\) only; that is \(f(x,y) = g(r)h(\theta)\), where \((x,y) \in \big\{(r, \theta )\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}\) with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\). Show that \[\iint_D f(x,y)\,dA = [G(R_2) - G(R_1)] \space [H(\theta_2) - H(\theta_1)], \nonumber \] where \(G\) and \(H\) are antiderivatives of \(g\) and \(h\), respectively.
65) Evaluate \(\displaystyle \iint_D \arctan \left(\frac{y}{x}\right) \sqrt{x^2 + y^2}\,dA,\) where \(D = \big\{(r,\theta)\,|\, 2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\).
- Answer
- \(\frac{133}{864}\pi^2\)
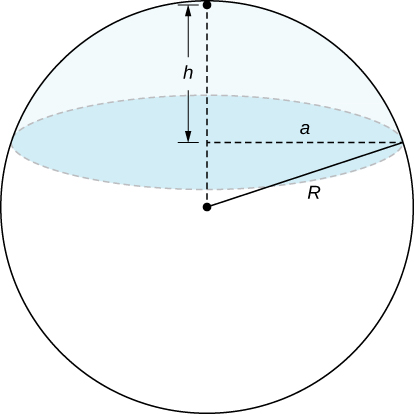
66) A spherical cap is the region of a sphere that lies above or below a given plane.
a. Show that the volume of the spherical cap in the figure below is \(\frac{1}{6} \pi h (3a^2 + h^2)\).
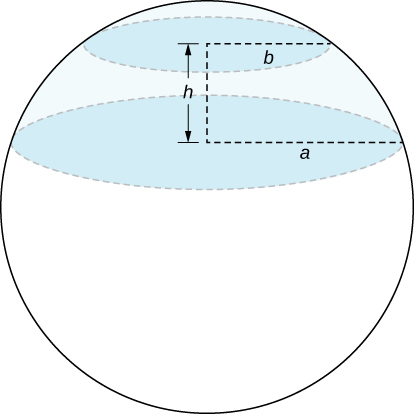
b. A spherical segment is the solid defined by intersecting a sphere with two parallel planes. If the distance between the planes is \(h\) show that the volume of the spherical segment in the figure below is \(\frac{1}{6}\pi h (3a^2 + 3b^2 + h^2)\).
67) In statistics, the joint density for two independent, normally distributed events with a mean \(\mu = 0\) and a standard distribution \(\sigma\) is defined by \(p(x,y) = \frac{1}{2\pi\sigma^2} e^{-\frac{x^2+y^2}{2\sigma^2}}\). Consider \((X,Y)\), the Cartesian coordinates of a ball in the resting position after it was released from a position on the z-axis toward the \(xy\)-plane. Assume that the coordinates of the ball are independently normally distributed with a mean \(\mu = 0\) and a standard deviation of \(\sigma\) (in feet). The probability that the ball will stop no more than \(a\) feet from the origin is given by \[P[X^2 + Y^2 \leq a^2] = \iint_D p(x,y) dy \space dx, \nonumber \] where \(D\) is the disk of radius \(a\) centered at the origin. Show that \[P[X^2 + Y^2 \leq a^2] = 1 - e^{-a^2/2\sigma^2}. \nonumber \]
68) The double improper integral \[\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}\,dy \, dx \nonumber \] may be defined as the limit value of the double integrals \(\displaystyle \iint_D e^{-x^2+y^2/2}\,dA\) over disks \(D_a\) of radii \(a\) centered at the origin, as \(a\) increases without bound; that is,
\[\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}dy \space dx = \lim_{a\rightarrow\infty} \iint_{D_a} e^{-x^2+y^2/2}\,dA. \nonumber \]
Use polar coordinates to show that \(\displaystyle \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}\,dy \, dx = 2\pi.\)
69) Show that \(\displaystyle \int_{-\infty}^{\infty} e^{-x^2/2}\,dx = \sqrt{2\pi}\) by using the relation
\[ \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}\,dy \,dx = \left(\int_{-\infty}^{\infty} e^{-x^2/2}dx \right) \left( \int_{-\infty}^{\infty} e^{-y^2/2}dy \right). \nonumber \]