15.4E: Exercises for Section 15.4

Last updated
Save as PDF

Page ID: 67149

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

For the following exercises, evaluate the line integrals by applying Green’s theorem.

1. $\displaystyle \int_C 2xy\,dx+(x+y)\,dy$, where $C$ is the path from $(0, 0)$ to $(1, 1)$ along the graph of $y=x^3$ and from $(1, 1)$ to $(0, 0)$ along the graph of $y=x$ oriented in the counterclockwise direction

2. $\displaystyle \int_C 2xy\,dx+(x+y)\,dy$, where $C$ is the boundary of the region lying between the graphs of $y=0$ and $y=4−x^2$ oriented in the counterclockwise direction

Answer: $\displaystyle \int_C2xy\,dx+(x+y)\,dy=\frac{32}{3}$ units of work

3. $\displaystyle \int_C 2\arctan\left(\frac{y}{x}\right)\,dx+\ln(x^2+y^2)\,dy$, where $C$ is defined by $x=4+2\cos θ,\;y=4\sin θ$ oriented in the counterclockwise direction

4. $\displaystyle \int_C \sin x\cos y\,dx+(xy+\cos x\sin y)\,dy$, where $C$ is the boundary of the region lying between the graphs of $y=x$ and $y=\sqrt{x}$ oriented in the counterclockwise direction

Answer: $\displaystyle \int_C\sin x\cos y\,dx+(xy+\cos x\sin y)\,dy=\frac{1}{12}$ units of work

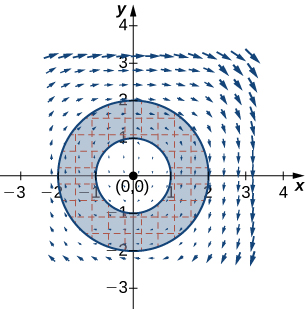
5. $\displaystyle \int_C xy\,dx+(x+y)\,dy$, where $C$ is the boundary of the region lying between the graphs of $x^2+y^2=1$ and $x^2+y^2=9$ oriented in the counterclockwise direction

6. $\displaystyle ∮_C (−y\,dx+x\,dy)$, where $C$ consists of line segment $C_1$ from $(−1,0)$ to $(1, 0)$, followed by the semicircular arc $C_2$ from $(1, 0)$ back to $(-1, 0)$

Answer: $\displaystyle ∮_C (−y\,\,dx+x\,\,dy)=π$ units of work

For the following exercises, use Green’s theorem.

7. Let $C$ be the curve consisting of line segments from $(0, 0)$ to $(1, 1)$ to $(0, 1)$ and back to $(0, 0)$. Find the value of $\displaystyle \int_C xy\,dx+\sqrt{y^2+1}\,dy$.

8. Evaluate line integral $\displaystyle \int_C xe^{−2x}\,dx+(x^4+2x^2y^2)\,dy$, where $C$ is the boundary of the region between circles $x^2+y^2=1$ and $x^2+y^2=4$, and is a positively oriented curve.

Answer: $\displaystyle \int_C xe^{−2x}\,dx+(x^4+2x^2y^2)\,dy=0$ units of work

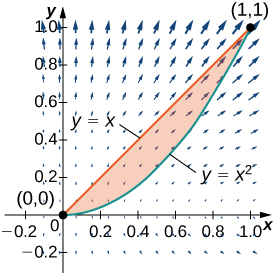
9. Find the counterclockwise circulation of field $\vecs F(x,y)=xy\,\mathbf{\hat i}+y^2\,\mathbf{\hat j}$ around and over the boundary of the region enclosed by curves $y=x^2$ and $y=x$ in the first quadrant and oriented in the counterclockwise direction.

$CNX_Calc_Figure_16_04_201.jpg$

10. Evaluate $\displaystyle ∮_C y^3\,dx−x^3y^2\,dy$, where $C$ is the positively oriented circle of radius $2$ centered at the origin.

Answer: $\displaystyle ∮_C y^3\,dx−x^3y^2\,dy=−20π$ units of work

11. Evaluate $\displaystyle ∮_C y^3\,dx−x^3\,dy$, where $C$ includes the two circles of radius $2$ and radius $1$ centered at the origin, both with positive orientation.

$CNX_Calc_Figure_16_04_202.jpg$

12. Calculate $\displaystyle ∮_C −x^2y\,dx+xy^2\,dy$, where $C$ is a circle of radius $2$ centered at the origin and oriented in the counterclockwise direction.

Answer: $\displaystyle ∮_C −x^2y\,dx+xy^2\,dy=8π$ units of work

13. Calculate integral $\displaystyle ∮_C 2[y+x\sin(y)]\,dx+[x^2\cos(y)−3y^2]\,dy$ along triangle $C$ with vertices $(0, 0), \,(1, 0)$ and $(1, 1)$, oriented counterclockwise, using Green’s theorem.

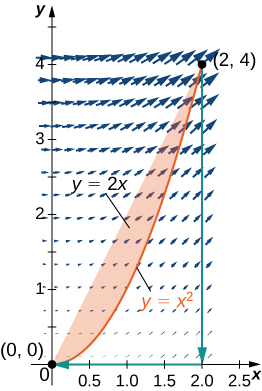
14. Evaluate integral $\displaystyle ∮_C (x^2+y^2)\,dx+2xy\,dy$, where $C$ is the curve that follows parabola $y=x^2$ from $(0,0), \,(2,4),$ then the line from $(2, 4)$ to $(2, 0)$, and finally the line from $(2, 0)$ to $(0, 0)$.

$CNX_Calc_Figure_16_04_203.jpg$

Answer: $\displaystyle ∮_C (x^2+y^2)\,dx+2xy\,dy=0$ units of work

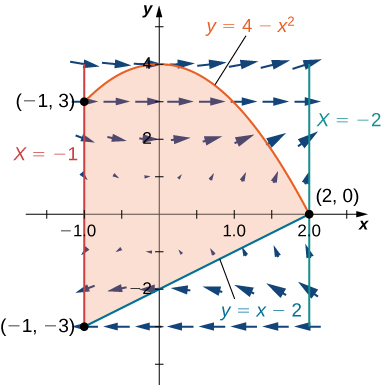
15. Evaluate line integral $\displaystyle ∮_C (y−\sin(y)\cos(y))\,dx+2x\sin^2(y)\,dy$, where $C$ is oriented in a counterclockwise path around the region bounded by $x=−1, \,x=2, \,y=4−x^2$, and $y=x−2.$

$CNX_Calc_Figure_16_04_204.jpg$

For the following exercises, use Green’s theorem to find the area.

16. Find the area between ellipse $\frac{x^2}{9}+\frac{y^2}{4}=1$ and circle $x^2+y^2=25$.

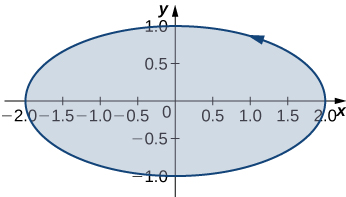
Answer: $A=19π\;\text{units}^2$

17. Find the area of the region enclosed by parametric equation

$\vecs p(θ)=(\cos(θ)−\cos^2(θ))\,\mathbf{\hat i}+(\sin(θ)−\cos(θ)\sin(θ))\,\mathbf{\hat j}$ for $0≤θ≤2π.$

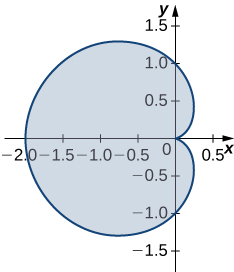
$CNX_Calc_Figure_16_04_205.jpg$

18. Find the area of the region bounded by hypocycloid $\vecs r(t)=\cos^3(t)\,\mathbf{\hat i}+\sin^3(t)\,\mathbf{\hat j}$. The curve is parameterized by $t∈[0,2π].$

Answer: $A=\frac{3}{8π}\;\text{units}^2$

19. Find the area of a pentagon with vertices $(0,4), \,(4,1), \,(3,0), \,(−1,−1),$ and $(−2,2)$.

20. Use Green’s theorem to evaluate $\displaystyle \int_{C^+}(y^2+x^3)\,dx+x^4\,dy$, where $C^+$ is the perimeter of square $[0,1]×[0,1]$ oriented counterclockwise.

Answer: $\displaystyle \int_{C^+} (y^2+x^3)\,dx+x^4\,dy=0$

21. Use Green’s theorem to prove the area of a disk with radius $a$ is $A=πa^2\;\text{units}^2$.

22. Use Green’s theorem to find the area of one loop of a four-leaf rose $r=3\sin 2θ$. (Hint: $x\,dy−y\,dx=r^2\,dθ$).

Answer: $A=\frac{9π}{8}\;\text{units}^2$

23. Use Green’s theorem to find the area under one arch of the cycloid given by the parametric equations: $x=t−\sin t,\;y=1−\cos t,\;t≥0.$

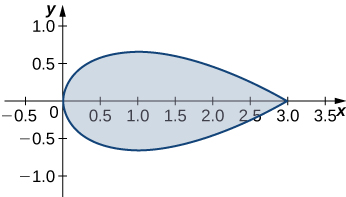
24. Use Green’s theorem to find the area of the region enclosed by curve

$\vecs r(t)=t^2\,\mathbf{\hat i}+\left(\frac{t^3}{3}−t\right)\,\mathbf{\hat j},$ for $−\sqrt{3}≤t≤\sqrt{3}$.

$CNX_Calc_Figure_16_04_206.jpg$

Answer: $A=\frac{8\sqrt{3}}{5}\;\text{units}^2$

25. [T] Evaluate Green’s theorem using a computer algebra system to evaluate the integral $\displaystyle \int_C xe^y\,dx+e^x\,dy$, where $C$ is the circle given by $x^2+y^2=4$ and is oriented in the counterclockwise direction.

26. Evaluate $\displaystyle \int_C(x^2y−2xy+y^2)\,ds$, where $C$ is the boundary of the unit square $0≤x≤1,\;0≤y≤1$, traversed counterclockwise.

Answer: $\displaystyle \int_C (x^2y−2xy+y^2)\,ds=3$

27. Evaluate $\displaystyle \int_C \frac{−(y+2)\,dx+(x−1)\,dy}{(x−1)^2+(y+2)^2}$, where $C$ is any simple closed curve with an interior that does not contain point $(1,−2)$ traversed counterclockwise.

28. Evaluate $\displaystyle \int_C \frac{x\,dx+y\,dy}{x^2+y^2}$, where $C$ is any piecewise, smooth simple closed curve enclosing the origin, traversed counterclockwise.

Answer: $\displaystyle \int_C \frac{x\,dx+y\,dy}{x^2+y^2}=2π$

For the following exercises, use Green’s theorem to calculate the work done by force $\vecs F$ on a particle that is moving counterclockwise around closed path $C$.

29. $\vecs F(x,y)=xy\,\mathbf{\hat i}+(x+y)\,\mathbf{\hat j}, \quad C:x^2+y^2=4$

30. $\vecs F(x,y)=(x^{3/2}−3y)\,\mathbf{\hat i}+(6x+5\sqrt{y})\,\mathbf{\hat j}, \quad C$: boundary of a triangle with vertices $(0, 0), \,(5, 0),$ and $(0, 5)$

Answer: $W=\frac{225}{2}$ units of work

31. Evaluate $\displaystyle \int_C (2x^3−y^3)\,dx+(x^3+y^3)\,dy$, where $C$ is a unit circle oriented in the counterclockwise direction.

32. A particle starts at point $(−2,0)$, moves along the $x$-axis to $(2, 0)$, and then travels along semicircle $y=\sqrt{4−x^2}$ to the starting point. Use Green’s theorem to find the work done on this particle by force field $\vecs F(x,y)=x\,\mathbf{\hat i}+(x^3+3xy^2)\,\mathbf{\hat j}$.

Answer: $W=12π$ units of work

33. David and Sandra are skating on a frictionless pond in the wind. David skates on the inside, going along a circle of radius $2$ in a counterclockwise direction. Sandra skates once around a circle of radius $3$, also in the counterclockwise direction. Suppose the force of the wind at point $(x,y)$ is $\vecs F(x,y)=(x^2y+10y)\,\mathbf{\hat i}+(x^3+2xy^2)\,\mathbf{\hat j}$. Use Green’s theorem to determine who does more work.

34. Use Green’s theorem to find the work done by force field $\vecs F(x,y)=(3y−4x)\,\mathbf{\hat i}+(4x−y)\,\mathbf{\hat j}$ when an object moves once counterclockwise around ellipse $4x^2+y^2=4.$

Answer: $W=2π$ units of work

35. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C e^{2x}\sin 2y\,dx+e^{2x}\cos 2y\,dy$, where $C$ is ellipse $9(x−1)^2+4(y−3)^2=36$ oriented counterclockwise.

36. Evaluate line integral $\displaystyle ∮_C y^2\,dx+x^2\,dy$, where $C$ is the boundary of a triangle with vertices $(0,0), \,(1,1)$, and $(1,0)$, with the counterclockwise orientation.

Answer: $\displaystyle ∮_C y^2\,dx+x^2\,dy=\frac{1}{3}$ units of work

37. Use Green’s theorem to evaluate line integral $\displaystyle \int_C \vecs h·d\vecs r$ if $\vecs h(x,y)=e^y\,\mathbf{\hat i}−\sin πx\,\mathbf{\hat j}$, where $C$ is a triangle with vertices $(1, 0), \,(0, 1),$ and $(−1,0),$ traversed counterclockwise.

38. Use Green’s theorem to evaluate line integral $\displaystyle \int_C\sqrt{1+x^3}\,dx+2xy\,dy$ where $C$ is a triangle with vertices $(0, 0), \,(1, 0),$ and $(1, 3)$ oriented clockwise.

Answer: $\displaystyle \int_C \sqrt{1+x^3}\,dx+2xy\,dy=3$ units of work

39. Use Green’s theorem to evaluate line integral $\displaystyle \int_C x^2y\,dx−xy^2\,dy$ where $C$ is a circle $x^2+y^2=4$ oriented counterclockwise.

40. Use Green’s theorem to evaluate line integral $\displaystyle \int_C \left(3y−e^{\sin x}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy$ where $C$ is circle $x^2+y^2=9$ oriented in the counterclockwise direction.

Answer: $\displaystyle \int_C \left(3y−e^{\sin x}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy=36π$ units of work

41. Use Green’s theorem to evaluate line integral $\displaystyle \int_C (3x−5y)\,dx+(x−6y)\,dy$, where $C$ is ellipse $\frac{x^2}{4}+y^2=1$ and is oriented in the counterclockwise direction.

$A horizontal oval oriented counterclockwise with vertices at (-2,0), (0,-1), (2,0), and (0,1). The region enclosed is shaded.$

42. Let $C$ be a triangular closed curve from $(0, 0)$ to $(1, 0)$ to $(1, 1)$ and finally back to $(0, 0).$ Let $\vecs F(x,y)=4y\,\mathbf{\hat i}+6x^2\,\mathbf{\hat j}.$ Use Green’s theorem to evaluate $\displaystyle ∮_C\vecs F·d\vecs r.$

Answer: $\displaystyle ∮_C\vecs F·d\vecs r=2$ units of work

43. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C y\,dx−x\,dy$, where $C$ is circle $x^2+y^2=a^2$ oriented in the clockwise direction.

44. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C (y+x)\,dx+(x+\sin y)\,dy,$ where $C$ is any smooth simple closed curve joining the origin to itself oriented in the counterclockwise direction.

Answer: $\displaystyle ∮_C (y+x)\,dx+(x+\sin y)\,dy=0$ units of work

45. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C \left(y−\ln(x^2+y^2)\right)\,dx+\left(2\arctan \frac{y}{x}\right)\,dy,$ where $C$ is the positively oriented circle $(x−2)^2+(y−3)^2=1.$

46. Use Green’s theorem to evaluate $\displaystyle ∮_C xy\,dx+x^3y^3\,dy,$ where $C$ is a triangle with vertices $(0, 0), \,(1, 0),$ and $(1, 2)$ with positive orientation.

Answer: $\displaystyle ∮_C xy\,dx+x^3y^3\,dy=2221$ units of work

47. Use Green’s theorem to evaluate line integral $\displaystyle \int_C \sin y\,dx+x\cos y\,dy,$ where $C$ is ellipse $x^2+xy+y^2=1$ oriented in the counterclockwise direction.

48. Let $\vecs F(x,y)=\left(\cos(x^5)−13y^3\right)\,\mathbf{\hat i}+13x^3\,\mathbf{\hat j}.$ Find the counterclockwise circulation $\displaystyle ∮_C\vecs F·d\vecs r,$ where $C$ is a curve consisting of the line segment joining $(−2,0)$ and $(−1,0),$ half circle $y=\sqrt{1−x^2},$ the line segment joining $(1, 0)$ and $(2, 0),$ and half circle $y=\sqrt{4−x^2}.$

Answer: $\displaystyle ∮_C\vecs F·d\vecs r=15π^4$ units of work

49. Use Green’s theorem to evaluate line integral $\displaystyle ∫_C \sin(x^3)\,dx+2ye^{x^2}\,dy,$ where $C$ is a triangular closed curve that connects the points $(0, 0), \,(2, 2),$ and $(0, 2)$ counterclockwise.

50. Let $C$ be the boundary of square $0≤x≤π,\;0≤y≤π,$ traversed counterclockwise. Use Green’s theorem to find $\displaystyle ∫_C \sin(x+y)\,dx+\cos(x+y)\,dy.$

Answer: $\displaystyle \int_C\sin(x+y)\,dx+\cos(x+y)\,dy=4$ units of work

51. Use Green’s theorem to evaluate line integral $\displaystyle ∫_C \vecs F·d\vecs r,$ where $\vecs F(x,y)=(y^2−x^2)\,\mathbf{\hat i}+(x^2+y^2)\,\mathbf{\hat j},$ and $C$ is a triangle bounded by $y=0,\;x=3,$ and $y=x,$ oriented counterclockwise.

52. Use Green’s Theorem to evaluate integral $\displaystyle ∫_C \vecs F·d\vecs r,$ where $\vecs F(x,y)=(xy^2)\,\mathbf{\hat i}+x\,\mathbf{\hat j},$ and $C$ is a unit circle oriented in the counterclockwise direction.

Answer: $\displaystyle ∫_C \vecs F·d\vecs r=π$ units of work

53. Use Green’s theorem in a plane to evaluate line integral $\displaystyle ∮_C (xy+y^2)\,dx+x^2\,dy,$ where $C$ is a closed curve of a region bounded by $y=x$ and $y=x^2$ oriented in the counterclockwise direction.

54. Calculate the outward flux of $\vecs F(x,y)=−x\,\mathbf{\hat i}+2y\,\mathbf{\hat j}$ over a square with corners $(±1,\,±1),$ where the unit normal is outward pointing and oriented in the counterclockwise direction.

Answer: $\displaystyle ∮_C\vecs F·\vecs N \,ds=4$

55. [T] Let $C$ be circle $x^2+y^2=4$ oriented in the counterclockwise direction. Evaluate $\displaystyle ∮_C \left[\left(3y−e^{\arctan x})\,dx+(7x+\sqrt{y^4+1}\right)\,dy\right]$ using a computer algebra system.

56. Find the flux of field $\vecs F(x,y)=−x\,\mathbf{\hat i}+y\,\mathbf{\hat j}$ across $x^2+y^2=16$ oriented in the counterclockwise direction.

Answer: $\displaystyle ∮_C \vecs F·\vecs N\,ds=32π$

57. Let $\vecs F=(y^2−x^2)\,\mathbf{\hat i}+(x^2+y^2)\,\mathbf{\hat j},$ and let $C$ be a triangle bounded by $y=0, \,x=3,$ and $y=x$ oriented in the counterclockwise direction. Find the outward flux of $\vecs F$ through $C$.

58. [T] Let $C$ be unit circle $x^2+y^2=1$ traversed once counterclockwise. Evaluate $\displaystyle ∫_C \left[−y^3+\sin(xy)+xy\cos(xy)\right]\,dx+\left[x^3+x^2\cos(xy)\right]\,dy$ by using a computer algebra system.

Answer: $\displaystyle ∫_C \left[−y^3+\sin(xy)+xy\cos(xy)\right]\,dx+\left[x^3+x^2\cos(xy)\right]\,dy=4.7124$ units of work

59. [T] Find the outward flux of vector field $\vecs F(x,y)=xy^2\,\mathbf{\hat i}+x^2y\,\mathbf{\hat j}$ across the boundary of annulus $R=\big\{(x,y):1≤x^2+y^2≤4\big\}=\big\{(r,θ):1≤r≤2,\,0≤θ≤2π\big\}$ using a computer algebra system.

60. Consider region $R$ bounded by parabolas $y=x^2$ and $x=y^2.$ Let $C$ be the boundary of $R$ oriented counterclockwise. Use Green’s theorem to evaluate $\displaystyle ∮_C \left(y+e^{\sqrt{x}}\right)\,dx+\left(2x+\cos(y^2)\right)\,dy.$

Answer: $\displaystyle ∮_C \left(y+e^{\sqrt{x}}\right)\,dx+\left(2x+\cos(y^2)\right)\,dy=13$ units of work

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.