5.4: Onto Functions and Images/Preimages of Sets
- Page ID
- 25308
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)One-to-one functions focus on the elements in the domain. We do not want any two of them sharing a common image. Onto functions focus on the codomain. We want to know if it contains elements not associated with any element in the domain.
Definition: ONTO (surjection)
A function \(f :{A}\to{B}\) is onto if, for every element \(b\in B\), there exists an element \(a\in A\) such that \[f(a) = b.\] An onto function is also called a surjection, and we say it is surjective.
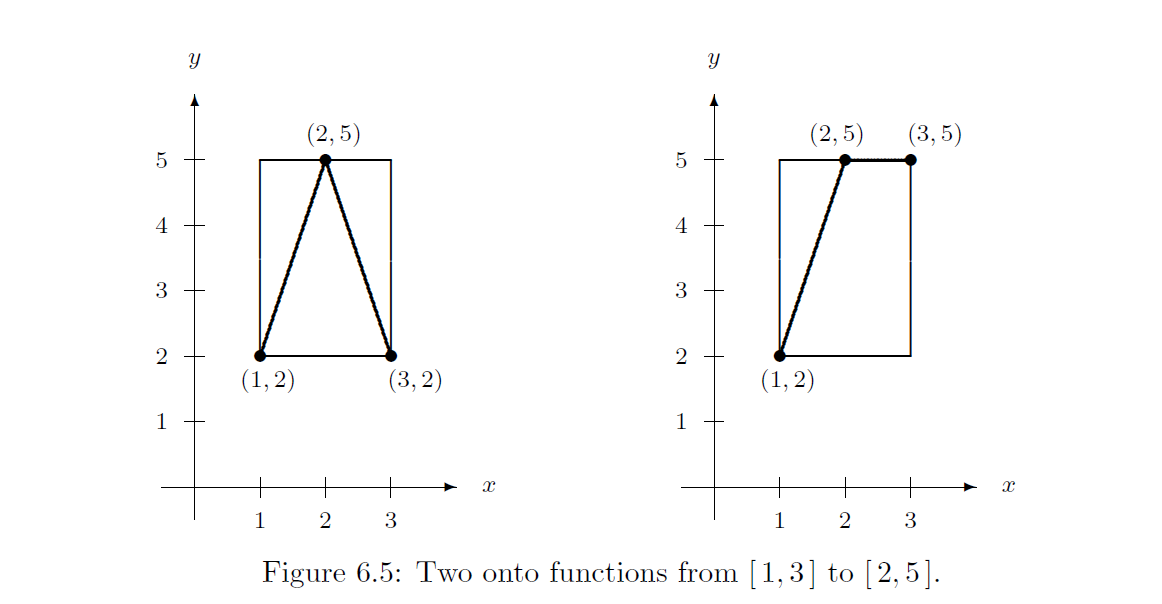
Example \(\PageIndex{1}\label{eg:ontofcn-01}\)
The graph of the piecewise-defined functions \(h :{[1,3]}\to{[2,5]}\) defined by
\[h(x) = \cases{ 3x- 1 & if $1\leq x\leq 2$, \cr -3x+11 & if $2 < x\leq 3$, \cr} \nonumber\]
is displayed on the left in Figure 6.5. It is clearly onto, because, given any \(y\in[2,5]\), we can find at least one \(x\in[1,3]\) such that \(h(x)=y\). Likewise, the function \(k :{[1,3]}\to{[2,5]}\) defined by
\[k(x) = \cases{ 3x- 1 & if $1\leq x\leq 2$, \cr 5 & if $2 < x\leq 3$, \cr}\nonumber\]
is also onto. Its graph is displayed on the right of Figure 6.5.
Hands-on exercise \(\PageIndex{1}\label{he:ontofcn-01}\)
The two functions in Example 5.4.1 are onto but not one-to-one. Construct a one-to-one and onto function \(f\) from \([1,3]\) to \([2,5]\).
Hands-on exercise \(\PageIndex{2}\label{he:ontofcn-02}\)
Construct a function \(g :{[1,3]}\to{[2,5]}\) that is one-to-one but not onto.
Hands-on exercise \(\PageIndex{3}\label{he:ontofcn-03}\)
Find a subset \(B\) of \(\mathbb{R}\) that would make the function \(s :{\mathbb{R}}\to{B}\) defined by \(s(x) = x^2\) an onto function.
Example \(\PageIndex{2}\label{eg:ontofcn-02}\)
Consider the function \(g :\mathbb{R} \times \mathbb{R} \to{\mathbb{R}}\) defined by \(g(x,y)=\frac{x+y}{2}.\)
Is this function onto?
Remark
This function maps ordered pairs to a single real numbers. The image of an ordered pair is the average of the two coordinates of the ordered pair. To decide if this function is onto, we need to determine if every element in the codomain has a preimage in the domain.
- Solution
-
Take any real number, \(x \in \mathbb{R}.\) Choose \((a,b) = (2x,0)\). \((a,b) \in \mathbb{R} \times \mathbb{R}\) since \(2x \in \mathbb{R}\) because the real numbers are closed under multiplication and \(0 \in \mathbb{R}.\) \(g(a,b)=g(2x,0)=\frac{2x+0}{2}=x\). Thus, for any real number, we have shown a preimage \( \mathbb{R} \times \mathbb{R}\) that maps to this real number. Therefore, this function is onto.
In general, how can we tell if a function \(f :{A}\to{B}\) is onto? The key question is: given an element \(y\) in the codomain, is it the image of some element \(x\) in the domain? If it is, we must be able to find an element \(x\) in the domain such that \(f(x)=y\). Mathematically, if the rule of assignment is in the form of a computation, then we need to solve the equation \(y=f(x)\) for \(x\). If we can always express \(x\) in terms of \(y\), and if the resulting \(x\)-value is in the domain, the function is onto.
To prove a function is onto
For \(f:A \to B\)
- Let \(y\) be any element in the codomain, \(B.\)
- Figure out an element in the domain that is a preimage of \(y\); often this involves some "scratch work" on the side.
- Choose \(x=\) the value you found.
- Demonstrate \(x\) is indeed an element of the domain, \(A.\)
- Show \(f(x)=y.\)
- Conclude with: we have found a preimage in the domain for an arbitrary element of the codomain, so every element of the codomain has a preimage in the domain. Therefore \(f\) is onto, by definition of onto.
Example \(\PageIndex{3}\label{eg:ontofcn-03}\)
The function \(g :{\mathbb{R}}\to{\mathbb{R}}\) is defined as \(g(x)=5x+11\). Prove that it is onto.
- Scratch Work
-
We need to find an \(x\) that maps to \(y.\) Suppose \(y=5x+11\); now we solve for \(x\) in terms of \(y\). We find \[x=\frac{y-11}{5}.\] (We'll need to verify \(x\) is a real number - an element in the domain.)
That's the \(x\) we want to choose so that \(g(x)=y\).
Now for the proof:
- Proof
-
Let \(y\) be any element of \(\mathbb{R}\).
Choose \(x=\frac{y-11}{5}.\)
Now, since the real numbers are closed under subtraction and non-zero division, \(x \in \mathbb{R}.\)
\(g(x)=g(\frac{y-11}{5})=5(\frac{y-11}{5})+11=y-11+11=y.\)
Thus, we have found an \(x \in \mathbb{R}\) such that \(g(x)=y.\)
So, given an arbitrary element of the codomain, we have shown a preimage in the domain.
Thus every element in the codomain has a preimage in the domain. Therefore, by the definition of onto, \(g\) is onto.
Hands-on exercise \(\PageIndex{4}\label{he:ontofcn-04}\)
Determine whether \(f: \mathbb{R} \to \mathbb{R}\) defined by \[f(x) = \cases{ 3x+1 & if $x\leq2$ \cr 4x & if $x > 2$ \cr}\nonumber\] is an onto function.
Example \(\PageIndex{4}\label{eg:ontofcn-04}\)
Is the function \({u}:{\mathbb{Z}}\to{\mathbb{Z}}\) defined by
\[u(n) = \cases{ 2n & if $n\geq0$ \cr -n & if $n < 0$ \cr} \nonumber\]
one-to-one? Is it onto?
- Solution
-
Since \(u(-2)=u(1)=2\), the function \(u\) is not one-to-one. Since \(u(n)\geq0\) for any \(n\in\mathbb{Z}\), the function \(u\) is not onto.
hands-on exercise \(\PageIndex{5}\label{he:ontofcn-05}\)
Is the function \(v:{\mathbb{N}}\to{\mathbb{N}}\) defined by \(v(n)=n+1\) onto? Explain.
Images and Preimages of Sets
Definition: Image of a Set
Given a function \(f :{A}\to{B}\), and \(C\subseteq A\), the image of \(C\) under \(f\) is defined as \[f(C) = \{ f(x) \mid x\in C \}.\] In words, \(f(C)\) is the set of all the images of the elements of \(C\).
A few remarks about the definition:
- It is about the image of a subset \(C\) of the domain of \(A\). Do not confuse it with the image of an element \(x\) from \(A\).
- Therefore, do not merely say “the image.” Be specific: the image of an element, or the image of a subset.
- Better yet: include the notation \(f(x)\) or \(f(C)\) in the discussion.
- While \(f(x)\) is an element in the codomain, \(f(C)\) is a subset of the codomain.
- Perhaps, the most important thing to remember is:
If \(y\in f(C)\), then \(y\in B\), and there exists an \(x\in C\)
such that \(f(x)=y\).
This key observation is often what we need to start a proof with.
Note:
Let \(f :A \to B\) be a function. The image of set \(A\) is the range of \(f\), which is the set of all possible images that \(f\) can assume.
Also, if the range of \(f\) is equal to \(B\), then \(f\) is onto.
Example \(\PageIndex{5}\)
For the function \(f :\mathbb{R} \to{\mathbb{R}}\) defined by
\[f(x) = x^2, \nonumber \]
we find the range of \(f\) is \([0,\infty)\). We also have, for example, \(f\big([\,2,\infty)\big) = [4,\infty)\). It is clear that \(f\) is neither one-to-one nor onto.
Example \(\PageIndex{6}\)
For the function \(g :{\mathbb{Z}}\to{\mathbb{Z}}\) defined by \[g(n) = n+3,\nonumber\] we find range of \(g\) is \(\mathbb{Z}\), and \(g(\mathbb{N})=\{4,5,6,\ldots\}\). The function \(g\) is both one-to-one and onto.
Example \(\PageIndex{7}\)
Determine \(f(\{(0,2), (1,3)\})\), where the function \(f :\{0,1,2\} \times\{0,1,2,3\} \to \mathbb{Z}\) is defined according to
\[f(a,b) = a+b. \nonumber\]
Remark: Strictly speaking, we should write \(f((a,b))\) because the argument is an ordered pair of the form \((a,b)\). However, we often write \(f(a,b)\), because \(f\) can be viewed as a two-variable function. The first variable comes from \(\{0,1,2\}\), the second comes from \(\{0,1,2,3\}\), and we add them to form the image. Notice we are asked for the image of a set with two elements.
- Solution
-
Because \[f(0,2)=0+2=2, \qquad\mbox{and}\qquad f(1,3)=1+3=4,\] we determine that \(f(\{(0,2),(1,3)\}) = \{2,4\}\).a Set
Definition: Preimage of a Set
Given a function \(f :{A}\to{B}\), and \(D\subseteq B\), the preimage \(D\) of under \(f\) is defined as \[f^{-1}(D) = \{ x\in A \mid f(x) \in D \}.\] Hence, \(f^{-1}(D)\) is the set of elements in the domain whose images are in \(C\). The symbol \(f^{-1}(D)\) is also pronounced as “\(f\) inverse of \(D\).”
Some remarks about the definition:
-
The preimage of \(D\) is a subset of the domain \(A\).
-
In particular, the preimage of \(B\) is always \(A\).
-
The key thing to remember is:
If \(x\in f^{-1}(D)\), then \(x\in A\), and \(f(x)\in D\).
-
It is possible that \(f^{-1}(D)=\emptyset\) for some subset \(D\). If this happens, \(f\) is not onto.
-
Therefore, \(f\) is onto if and only if \(f^{-1}(\{b\})\neq \emptyset\) for every \(b\in B\).
Example \(\PageIndex{8}\)
If \(t :{\mathbb{R}\to}{\mathbb{R}}\) is defined by \(t(x)=x^2-5x+5\), find \(t^{-1}(\{-1\})\).
- Solution
-
We want to find \(x\) such that \(t(x)=x^2-5x+5=-1\). Hence, we have to solve the equation \[0 = x^2-5x+6 = (x-2)(x-3).\nonumber\] The solutions are \(x=2\) and \(x=3\). Therefore, \(t^{-1}(\{-1\}) = \{2,3\}\).
hands-on Exercise \(\PageIndex{6}\label{he:propfcn-06}\)
If \(k :{\mathbb{Q}}\to{\mathbb{R}}\) is defined by \(k(x)=x^2-x-7\), find \(k^{-1}(\{3\})\).
Example \(\PageIndex{9}\)
For the function \(f :{\{0,1,2\}\times\{0,1,2,3\}}\to{\mathbb{Z}}\) defined by \[f(a,b) = a+b,\] we find \[\begin{aligned} f^{-1}(\{3\}) &=& \{(0,3), (1,2), (2,1)\}, \\ f^{-1}(\{4\}) &=& \{(1,3), (2,2)\}. \end{aligned}\] Since preimages are sets, we need to write the answers in set notation.
Summary and Review
- A function \(f :{A}\to{B}\) is onto if, for every element \(b\in B\), there exists an element \(a\in A\) such that \(f(a)=b\).
- Know how to prove \(f\) is an onto function.
- To show that a function is not onto, all we need is to find an element \(y\in B\), and show that no \(x\)-value from \(A\) would satisfy \(f(x)=y\).
- In addition to finding images & preimages of elements, we also find images & preimages of sets.
- Given a function \(f :{A}\to{B}\), the image of \(C\subseteq A\) is defined as \(f(C) = \{f(x) \mid x\in C\}\).
- If \(y\in f(C)\), then \(y\in B\), and there exists an \(x\in C\) such that \(f(x)=y\).
- The preimage of \(D\subseteq B\) is defined as \(f^{-1}(D) = \{x\in A \mid f(x)\in D\}\).
- If \(x\in f^{-1}(D)\), then \(x\in A\), and \(f(x)\in D\).
Exercises
exercise \(\PageIndex{1}\label{ex:ontofcn-01}\)
Determine which of the following are onto functions.
- \(f :{\mathbb{Z}}\to{\mathbb{Z}}\); \(f(n)=n^3+1\)
- \(g :{\mathbb{Q}}\to{\mathbb{Q}}\); \(g(x)=n^2\)
- \(h :{\mathbb{R}}\to{\mathbb{R}}\); \(h(x)=x^3-x\)
- \(k :{\mathbb{R}}\to{\mathbb{R}}\); \(k(x)=5^x\)
- Solution
-
(a) Not onto (b) Not onto (c) Onto (d) Not onto .
exercise \(\PageIndex{2}\label{ex:ontofcn-02}\)
Determine which of the following are onto functions.
- \(p :{\mathscr{P}(\{1,2,3,\ldots,n\})}\to{\{0,1,2,\ldots,n\}}\); \(p(S)=|S|\)
- \(q :{\mathscr{P}(\{1,2,3,\ldots,n\})}\to{\mathscr{P}(\{1,2,3,\ldots,n\})}\); \(q(S)=\overline{S}\)
exercise \(\PageIndex{3}\label{ex:ontofcn-03}\)
Determine which of the following functions are onto.
- \(f_1:\{1,2,3,4,5\}\to\{a,b,c,d\}\); \(f_1(1)=b\), \(f_1(2)=c\), \(f_1(3)=a\), \(f_1(4)=a\), \(f_1(5)=c\)
- \({f_2}:{\{1,2,3,4\}}\to{\{a,b,c,d,e\}}\); \(f_2(1)=c\), \(f_2(2)=b\), \(f_2(3)=a\), \(f_2(4)=d\)
- \({f_3}:{\mathbb{Z}}\to{\mathbb{Z}}\); \(f_3(n)=-n\)
- Solution
-
\(f_1\) and \(f_2\) are not onto, \(f_3\) is onto.
exercise \(\PageIndex{4}\label{ex:ontofcn-04}\)
Determine which of the following functions are onto.
- \({g_1}:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}\); \(g_1(1)=b\), \(g_1(2)=b\), \(g_1(3)=b\), \(g_1(4)=a\), \(g_1(5)=d\)
- \({g_2}:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}\); \(g_2(1)=d\), \(g_2(2)=b\), \(g_2(3)=e\), \(g_2(4)=a\), \(g_2(5)=c\)
Exercise \(\PageIndex{5}\)
Is it possible for a function from \(\{1,2\}\) to \(\{a,b,c,d\}\) to be onto? Explain.
- Answer
-
No, because we have at most two distinct images, but the codomain has four elements.
exercise \(\PageIndex{6}\label{ex:ontofcn-6}\)
List all the onto functions from \(\{1,2,3,4\}\) to \(\{a,b\}\)?
- Hint
-
List the images of each function.
exercise \(\PageIndex{7}\label{ex:ontofcn-7}\)
Determine which of the following functions are onto.
- \(f :{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(h(n)\equiv 3n\) (mod 10).
- \(g :{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(g(n)\equiv 5n\) (mod 10).
- \(h :{\mathbb{Z}_{36}}\to{\mathbb{Z}_{36}}\); \(h(n)\equiv 3n\) (mod 36).
- Solution
-
(a) Onto (b) Not onto (c) Not onto
exercise \(\PageIndex{8}\label{ex:ontofcn-8}\)
Determine which of the following functions are onto.
- \(r:{\mathbb{Z}_{36}}\to{\mathbb{Z}_{36}}\); \(r(n)\equiv 5n\) (mod 36).
- \(s :{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(s(n)\equiv n+5\) (mod 10).
- \(t :{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(t(n)\equiv 3n+5\) (mod 10).
exercise \(\PageIndex{9}\label{ex:ontofcn-9}\)
Given a function \(f :{A}\to{B}\), and \(C\subset A\), since \(f(C)\) is a subset of \(B\), the preimage of this subset is indicated by the notation \(f^{-1}(f(C))\). Consider the function \(f :{\mathbb{Z}}\to{\mathbb{Z}}\) defined by \(f(x)=x^2\), and \(C=\{0,1,2,3\}\).
(a) Find \(f(C)\).
(b) Find \(f^{-1}(f(C))\).
- Solution
-
(a) \(f(C)=\{0,2,4,9\}\).
(b) \(f^{-1}(f(C))=\{-3,-2,-1,0,1,2,3\}\).
exercise \(\PageIndex{10}\label{ex:ontofcn-10}\)
Give an example of a function \(f :\mathbb{N}\to \mathbb{N}\) that is
- neither one-to-one nor onto
- one-to-one but not onto
- onto but not one-to-one
- both one-to-one and onto
Exercise \(\PageIndex{11}\)
For each of the following functions, find the image of \(C\), and the preimage of \(D\).
(a) \({f_1}:{\{1,2,3,4,5\}}\to{\{a,b,c,d\}}\); \(f_1(1)=b\), \(f_1(2)=c\), \(f_1(3)=a\), \(f_1(4)=a\), \(f_1(5)=c\); \(C=\{1,3\}\), \(D=\{a,c\}\).
(b) \({f_2}:{\{1,2,3,4\}}\to{\{a,b,c,d,e\}}\); \(f_2(1)=c\), \(f_2(2)=b\), \(f_2(3)=a\), \(f_2(4)=d\);\(C=\{1,3\}\), \(D=\{b,d\}\).
(c) \({f_3}:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}\); \(f_3(1)=b\), \(f_3(2)=b\), \(f_3(3)=b\), \(f_3(4)=a\), \(f_3(5)=d\); \(C=\{1,3,5\}\), \(D=\{c\}\).
(d) \({f_4}:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}\); \(f_4(1)=d\), \(f_4(2)=b\), \(f_4(3)=e\), \(f_4(4)=a\), \(f_4(5)=c\); \(C=\{3\}\), \(D=\{c\}\).
- Solution
-
(a) \(f_1(C)=\{a,b\}\) ; \(f_1^{-1}(D)=\{2,3,4,5\}\)
(b) \(f_2(C)=\{a,c\}\) ; \(f_2^{-1}(D)=\{2,4\}\)
(c) \(f_3(C)=\{b,d\}\) ; \(f_3^{-1}(D)=\emptyset\)
(d) \(f_4(C)=\{e\}\) ; \(f_4^{-1}(D)=\{5\}\)
Exercise \(\PageIndex{12}\)
Define the \(r :{\mathbb{Z}\times\mathbb{Z}}\to{\mathbb{Q}}\) according to \(r(m,n) = 3^m 5^n\).
- Find \(r(\{1,2,3\}\times\{-1,0,1\})\).
- Find \(r^{-1}\big(\big\{\frac{25}{27}\big\}\big)\).
- Find \(r^{-1}(D)\), where \(D=\{3,9,27,81,\ldots\,\}\).
Exercise \(\PageIndex{13}\)
The function \(u :{\mathbb{R}}\to{\mathbb{R}}\) is defined as \(u(x)=3x+11\), and the function \(v :{\mathbb{Z}}\to{\mathbb{R}}\) is defined as \(v(x)=3x+11\).
- Find \(u([\,3,5))\) and \(v(\{3,4,5\})\).
- Find \(u^{-1}((2,7\,])\) and \(v^{-1}((2,7\,])\).
- Solution
-
(a) \(u([\,3,5))=[\,20,26]\) and \(v(\{3,4,5\})=\{20,23,26\}\).
(b) \(u^{-1}((2,7\,])=(-3,-\frac{4}{3}]\) and \(v^{-1}((2,7\,]=\{-2\})\).
Exercise \(\PageIndex{14}\)
Is the function \(h :{\mathbb{Z}}\to{\mathbb{Z}}\) defined by \[h(n) = \cases{ 2n & if $n\geq0$ \cr -n & if $n < 0$ \cr}\] one-to-one? Is it onto?
Exercise \(\PageIndex{15}\)
The function \(f :\mathbb{R} \times \mathbb{R} \to\mathbb{R} \times \mathbb{R}\) is defined as \(f(x,y)=(x+y,3y)\).
(a) Find \(f(3,4)\), \(f(-2,5)\), \(f(2,0)\).
(b) Is \(f\) onto?
(c) Is \(f\) one-to-one?
- Answer
-
(a) \(f(3,4)=(7,12)\), \(f(-2,5)=(3,15)\), \(f(2,0)=(2,0)\).
(b) Consider any \((a,b)\) in the codomain. Let \((x,y)=(a-\frac{b}{3} ,\frac{b}{3})\). Since \(\mathbb{R}\) is closed under subtraction and non-zero division, \(a-\frac{b}{3} \in \mathbb{R}\) and \(\frac{b}{3} \in \mathbb{R}\) , thus \((x,y) \in \mathbb{R} \times \mathbb{R}\).
Then \(f(x,y)=f(a-\frac{b}{3} ,\frac{b}{3})=(a,b)\). So, every element in the codomain has a preimage in the domain and thus \(f\) is onto.
(c) Yes, if \(f(x_1,y_1)=f(x_2,y_2) \mbox{ then } (x_1+y_1,3y_1)=(x_2+y_2,3y_2).\) This means \(3y_1=3y_2\) and (dividing by 3) \(y_1=y_2.\)
Now, since \(x_1+y_1=x_2+y_2,\) subtract equals, \(y_1\) and \(y_2\) from both sides to get \(x_1=x_2.\) Because \(x_1=x_2\) and \(y_1=y_2\), we have \((x_1,y_1)=(x_2,y_2).\)
\(f(x_1,y_1)=f(x_2,y_2) \rightarrow (x_1,y_1)=(x_2,y_2),\) so \(f\) is one-to-one.


