11.26: A.3.3- Section 3.3 Answers
- Last updated
- Dec 31, 2022
- Save as PDF
- Page ID
- 121424
( \newcommand{\kernel}{\mathrm{null}\,}\)
1. y1=1.550598190,y2=2.469649729
2. y1=1.221551366,y2=1.492920208
3. y1=1.890339767,y2=1.763094323
4. y1=2.961316248,y2=2.920128958
5. y1=2.475605264,y2=1.825992433
6.
| x | h=0.1 | h=0.05 | h=0.025 | Exact |
| 1.0 | 54.654509699 | 54.648344019 | 54.647962328 | 54.647937102 |
7.
| x | h=0.1 | h=0.05 | h=0.025 | Exact |
| 2.0 | 1.353191745 | 1.353193606 | 1.353193712 | 1.353193719 |
8.
| x | h=0.05 | h=0.025 | h=0.0125 | Exact |
| 1.50 | 10.498658198 | 10.499906266 | 10.499993820 | 10.500000000 |
9.
| x | h=0.1 | h=0.05 | h=0.025 | h=0.1 | h=0.05 | h=0.025 |
| 3.0 | 1.456023907 | 1.456023403 | 1.456023379 | 0.0000124 | 0.000000611 | 0.0000000333 |
| Approximate Solutions | Residuals | |||||
10.
| x | h=0.1 | h=0.05 | h=0.025 | h=0.1 | h=0.05 | h=0.025 |
| 2.0 | 0.492663789 | 0.492663738 | 0.492663736 | 0.000000902 | 0.0000000508 | 0.00000000302 |
| Approximate Solutions | Residuals | |||||
11.
| x | h=0.1 | h=0.05 | h=0.025 | "Exact" |
| 1.0 | 0.659957046 | 0.659957646 | 0.659957686 | 0.659957689 |
12.
| x | h=0.1 | h=0.05 | h=0.025 | "Exact" |
| 2.0 | −0.750911103 | −0.750912294 | −0.750912367 | −0.750912371 |
13. Applying variation of parameters to the given initial value problem yields y=ue−3x, where (A)u′=1−4x+3x2−4x3,u(0)=−3. Since u(5)=0, the Runge-Kutta method yields the exact solution of (A). Therefore the Euler semilinear method produces the exact solution of the given problem.
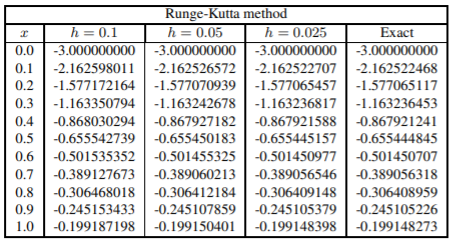
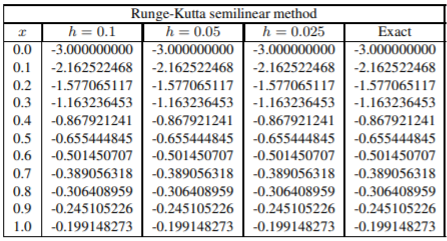
14.
| Runge-Kutta method | ||||
| x | h=0.1 | h=0.05 | h=0.025 | "Exact" |
| 3.0 | 15.281660036 | 15.281981407 | 15.282003300 | 15.282004826 |
| Runge-Kutta semilinear method | ||||
| x | h=0.1 | h=0.05 | h=0.025 | "Exact" |
| 3.0 | 15.282005990 | 15.282004899 | 15.282004831 | 15.282004826 |
15.
| Runge-Kutta method | ||||
| x | h=0.2 | h=0.1 | h=0.05 | "Exact" |
| 2.0 | 0.904678156 | 0.904295772 | 0.904277759 | 0.904276722 |
| Runge-Kutta semilinear method | ||||
| x | h=0.2 | h=0.1 | h=0.05 | "Exact" |
| 2.0 | 0.904592215 | 0.904297062 | 0.904278004 | 0.904276722 |
16.
| Runge-Kutta method | ||||
| x | h=0.2 | h=0.1 | h=0.05 | "Exact" |
| 3.0 | 0.967523147 | 0.967523152 | 0.967523153 | 0.967523153 |
| Runge-Kutta semilinear method | ||||
| x | h=0.2 | h=0.1 | h=0.05 | "Exact" |
| 3.0 | 0.967523147 | 0.967523152 | 0.967523153 | 0.967523153 |
17.
| Runge-Kutta method | ||||
| x | h=0.0500 | h=0.0250 | h=0.0125 | "Exact" |
| 1.50 | 0.343839158 | 0.343784814 | 0.343780796 | 0.343780513 |
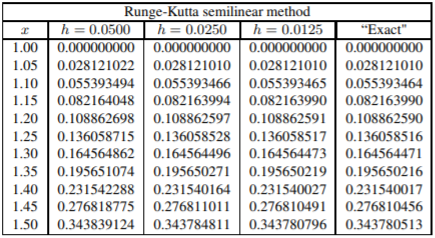
18.
| Runge-Kutta method | ||||
| x | h=0.2 | h=0.1 | h=0.05 | "Exact" |
| 2.0 | 0.732633229 | 0.732638318 | 0.732638609 | 0.732638628 |
| Runge-Kutta semilinear method | ||||
| x | h=0.2 | h=0.1 | h=0.05 | "Exact" |
| 2.0 | 0.732639212 | 0.732638663 | 0.732638630 | 0.732638628 |
19.
| Runge-Kutta method | ||||
| x | h=0.0500 | h=0.0250 | h=0.0125 | "Exact" |
| 1.50 | 2.244025683 | 2.244024088 | 2.244023989 | 2.244023982 |
| Runge-Kutta semilinear method | ||||
| x | h=0.0500 | h=0.0250 | h=0.0125 | "Exact" |
| 1.50 | 2.244025081 | 2.244024051 | 2.244023987 | 2.244023982 |
20.
| Runge-Kutta method | ||||
| x | h=0.1 | h=0.05 | h=0.025 | "Exact" |
| 1.0 | 0.056426886 | 0.056416137 | 0.056415552 | 0.056415515 |
| Runge-Kutta semilinear method | ||||
| x | h=0.1 | h=0.05 | h=0.025 | "Exact" |
| 1.0 | 0.056415185 | 0.056415495 | 0.056415514 | 0.056415515 |
21.
| Runge-Kutta method | ||||
| x | h=0.1 | h=0.05 | h=0.025 | "Exact" |
| 1.0 | 54.695901186 | 54.727111858 | 54.729426250 | 54.729594761 |
| Runge-Kutta semilinear method | ||||
| x | h=0.1 | h=0.05 | h=0.025 | "Exact" |
| 1.0 | 54.729099966 | 54.729561720 | 54.729592658 | 54.729594761 |
22.
| Runge-Kutta method | ||||
| x | h=0.1 | h=0.05 | h=0.025 | "Exact" |
| 3.0 | 1.361384082 | 1.361383812 | 1.361383809 | 1.361383810 |
| Runge-Kutta semilinear method | ||||
| x | h=0.1 | h=0.05 | h=0.025 | "Exact" |
| 3.0 | 1.361456502 | 1.361388196 | 1.361384079 | 1.361383810 |
24.
| x | h=.1 | h=.05 | h=.025 | Exact |
| 2.00 | −1.000000000 | −1.000000000 | −1.000000000 | −1.000000000 |
25.
| x | h=.1 | h=.05 | h=.025 | "Exact" |
| 1.00 | 1.000000000 | 1.000000000 | 1.000000000 | 1.000000000 |
26.
| x | h=.1 | h=.05 | h=.025 | "Exact" |
| 1.50 | 4.142171279 | 4.142170553 | 4.142170508 | 4.142170505 |
27.
| x | h=.1 | h=.05 | h=.025 | "Exact" |
| 3.0 | 16.666666988 | 16.666666687 | 16.666666668 | 16.666666667 |


