Double Integrals Part 2 (Exercises)
- Last updated
- Jun 14, 2019
- Save as PDF
- Page ID
- 21143
( \newcommand{\kernel}{\mathrm{null}\,}\)
1) The region D bounded by y=x3, y=x3+1, x=0, and x=1 as given in the following figure.
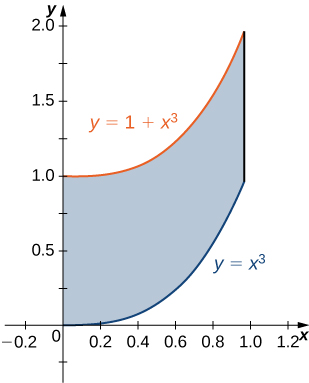
a. Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type I but not Type II
b. Find the area of the region D.
c. Find the average value of the function f(x,y)=3xy on the region graphed in the previous exercise.
- Answer
- 2720
2) The region D bounded by y=sinx, y=1+sinx, x=0, and x=π2 as given in the following figure.
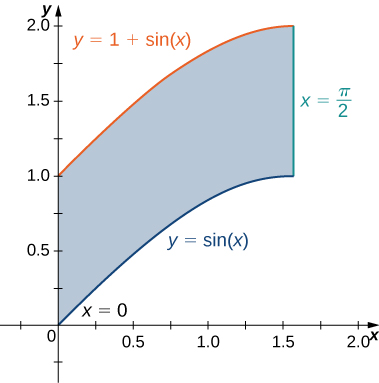
a. Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type I but not Type II
b. Find the area of the region D.
- Answer
- π2units2
c. Find the average value of the function f(x,y)=cosx on the region D.
3) The region D bounded by x=y2−1 and x=√1−y2 as given in the following figure.
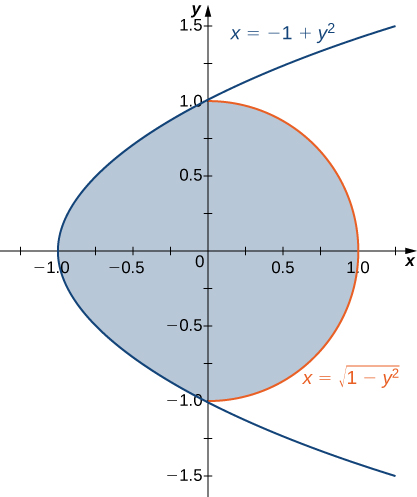
a. Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type II but not Type I
b. Find the volume of the solid under the graph of the function f(x,y)=xy+1 and above the region D.
- Answer
- 16(8+3π)units3
4) The region D bounded by y=0, x=−10+y, and x=10−y as given in the following figure.
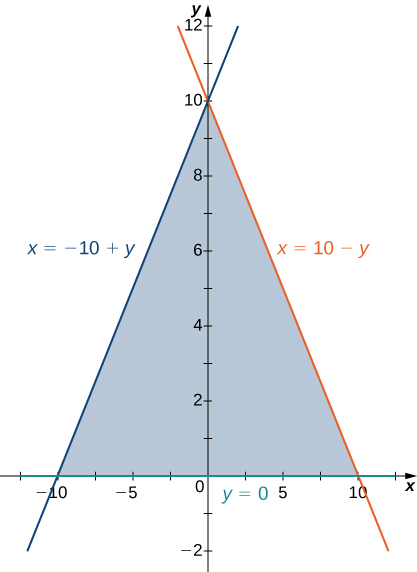
a. Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type II but not Type I
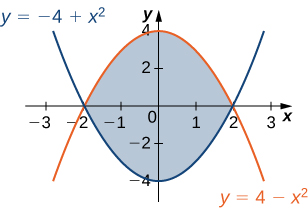
b. Find the volume of the solid under the graph of the function f(x,y)=x+y and above the region in the figure from the previous exercise.
- Answer
- 10003units3
5) The region D bounded by y=0, x=y−1, x=π2 as given in the following figure.
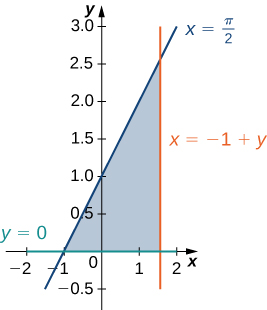
Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type I and Type II
6) The region D bounded by y=0 and y=x2−1 as given in the following figure.
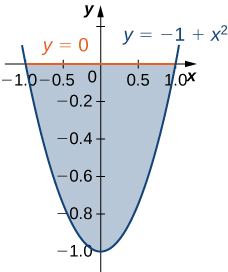
Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type I and Type II
7) Let D be the region bounded by the curves of equations y=cosx and y=4−x2 and the x-axis. Explain why D is neither of Type I nor II.
- Answer
- The region D is not of Type I: it does not lie between two vertical lines and the graphs of two continuous functions g1(x) and g2(x). The region is not of Type II: it does not lie between two horizontal lines and the graphs of two continuous functions h1(y) and h2(y).
8) Let D be the region bounded by the curves of equations y=x, y=−x and y=2−x2. Explain why D is neither of Type I nor II.
In exercises 9 - 14, evaluate the double integral ∬Df(x,y)dA over the region D.
9) f(x,y)=1 and
D={(x,y)|0≤x≤π2, sinx≤y≤1+sinx}
- Answer
- π2
10) f(x,y)=2 and
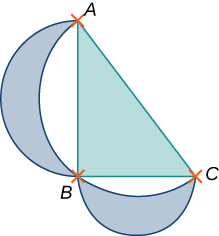
D={(x,y)|0≤y≤1, y−1≤x≤arccosy}
11) f(x,y)=xy and
D={(x,y)|−1≤y≤1, y2−1≤x≤√1−y2}
- Answer
- 0
12) f(x,y)=siny and D is the triangular region with vertices (0,0), (0,3), and (3,0)
13) f(x,y)=−x+1 and D is the triangular region with vertices (0,0), (0,2), and (2,2)
- Answer
- 23
14) f(x,y)=2x+4y and
D={(x,y)|0≤x≤1, x3≤y≤x3+1}
In exercises 15 - 20, evaluate the iterated integrals.
15) ∫10∫2√x+12√x(xy+1)dy dx
- Answer
- 4120
16) ∫30∫3x2x(x+y2)dy dx
17) ∫21∫−u−u2−1(8uv)dv du
- Answer
- −63
18) ∫e2e∫2lnu(v+lnu)dv du
19) ∫1/20∫√1−4y2−√1−4y24dx dy
- Answer
- π
20) ∫10∫√1−y2−√1−y2(2x+4y3)dx dy
21) Let D be the region bounded by y=1−x2, y=4−x2, and the x- and y-axes.
a. Show that ∬DxdA=∫10∫4−x21−x2x dy dx+∫21∫4−x20x dy dx by dividing the region D into two regions of Type I.
b. Evaluate the integral ∬DxdA.
22) Let D be the region bounded by y=1, y=x, y=lnx, and the x-axis.
a. Show that ∬Dy2dA=∫0−1∫2−x2−xy2dy dx+∫10∫2−x2xy2dy dx by dividing the region D into two regions of Type I, where D={(x,y)|y≥x,y≥−x, y≤2−x2}.
b. Evaluate the integral ∬Dy2dA.
23) Let D be the region bounded by y=x2, y=x+2, and y=−x.
a. Show that ∬DxdA=∫10∫√y−yx dx dy+∫41∫√yy−2x dx dy by dividing the region D into two regions of Type II, where D={(x,y)|y≥x2, y≥−x, y≤x+2}.
b. Evaluate the integral ∬DxdA.
- Answer
- a. Answers may vary;
b. 73
24) The region D bounded by x=0,y=x5+1, and y=3−x2 is shown in the following figure. Find the area A(D) of the region D.
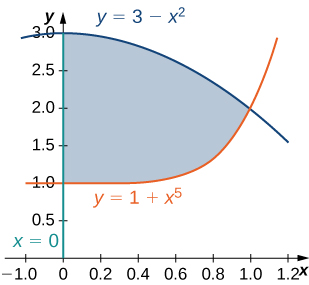
25) The region D bounded by y=cosx, y=4+cosx, and x=±π3 is shown in the following figure. Find the area A(D) of the region D.
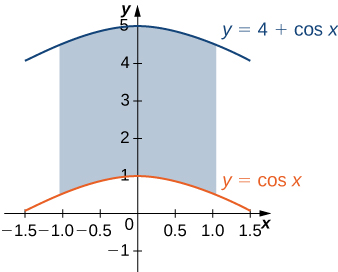
- Answer
- 8π3
26) Find the area A(D) of the region D={(x,y)|y≥1−x2,y≤4−x2, y≥0, x≥0}.
27) Let D be the region bounded by y=1, y=x, y=lnx, and the x-axis. Find the area A(D) of the region D.
- Answer
- (e−32)units2
28) Find the average value of the function f(x,y)=siny on the triangular region with vertices (0,0), (0,3), and (3,0).
29) Find the average value of the function f(x,y)=−x+1 on the triangular region with vertices (0,0), (0,2), and (2,2).
- Answer
- The average value of f on this triangular region is 13.
In exercises 30 - 33, change the order of integration and evaluate the integral.
30) ∫π/2−1∫x+10sinxdydx
31) ∫10∫1−xx−1xdydx
- Answer
- ∫10∫1−xx−1x dy dx=∫0−1∫y+10x dx dy+∫10∫1−y0x dx dy=13
32) ∫0−1∫√y+1−√y+1y2dx dy
33) ∫1/2−1/2∫√y2+1−√y2+1y dx dy
- Answer
- ∫1/2−1/2∫√y2+1−√y2+1y dx dy=∫21∫√x2−1−√x2−1y dy dx=0
34) The region D is shown in the following figure. Evaluate the double integral ∬D(x2+y)dA by using the easier order of integration.
35) The region D is shown in the following figure. Evaluate the double integral ∬D(x2−y2)dA by using the easier order of integration.
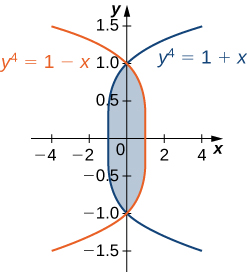
- Answer
- ∬D(x2−y2)dA=∫1−1∫1−y4y4−1(x2−y2)dx dy=4644095
36) Find the volume of the solid under the surface z=2x+y2 and above the region bounded by y=x5 and y=x.
37) Find the volume of the solid under the plane z=3x+y and above the region determined by y=x7 and y=x.
- Answer
- 45units3
38) Find the volume of the solid under the plane z=3x+y and above the region bounded by x=tany, x=−tany, and x=1.
39) Find the volume of the solid under the surface z=x3 and above the plane region bounded by x=siny, x=−siny, and x=1.
- Answer
- 5π32units3
40) Let g be a positive, increasing, and differentiable function on the interval [a,b]. Show that the volume of the solid under the surface z=g′(x) and above the region bounded by y=0, y=g(x), x=a, and x=b is given by 12(g2(b)−g2(a)).
41) Let g be a positive, increasing, and differentiable function on the interval [a,b] and let k be a positive real number. Show that the volume of the solid under the surface z=g′(x) and above the region bounded by y=g(x), y=g(x)+k, x=a, and x=b is given by k(g(b)−g(a)).
42) Find the volume of the solid situated in the first octant and determined by the planes z=2, z=0, x+y=1, x=0, and y=0.
43) Find the volume of the solid situated in the first octant and bounded by the planes x+2y=1, x=0, z=4, and z=0.
- Answer
- 1units3
44) Find the volume of the solid bounded by the planes x+y=1, x−y=1, x=0, z=0, and z=10.
45) Find the volume of the solid bounded by the planes x+y=1, x−y=1, x+y=−1 x−y=−1, z=1, and z=0
- Answer
- 2units3
46) Let S1 and S2 be the solids situated in the first octant under the planes x+y+z=1 and x+y+2z=1 respectively, and let S be the solid situated between S1, S2, x=0, and y=0.
- Find the volume of the solid S1.
- Find the volume of the solid S2.
- Find the volume of the solid S by subtracting the volumes of the solids S1 and S2.
47) Let S1 and S2 be the solids situated in the first octant under the planes 2x+2y+z=2 and x+y+z=1 respectively, and let S be the solid situated between S1, S2, x=0, and y=0.
- Find the volume of the solid S1.
- Find the volume of the solid S2.
- Find the volume of the solid S by subtracting the volumes of the solids S1 and S2.
- Answer
- a. 13units3
b. 16units3
c. 16units3
48) Let S1 and S2 be the solids situated in the first octant under the plane x+y+z=2 and under the sphere x2+y2+z2=4, respectively. If the volume of the solid S2 is 4π3 determine the volume of the solid S situated between S1 and S2 by subtracting the volumes of these solids.
49) Let S1 and S2 be the solids situated in the first octant under the plane x+y+z=2 and bounded by the cylinder x2+y2=4, respectively.
- Find the volume of the solid S1.
- Find the volume of the solid S2.
- Find the volume of the solid S situated between S1 and S2 by subtracting the volumes of the solids S1 and S2.
- Answer
- a. \frac{4}{3}\, \text{units}^3
b. 2\pi\, \text{units}^3
c. \frac{6\pi - 4}{3}\, \text{units}^3
50) [T] The following figure shows the region D bounded by the curves y = \sin x, \space x = 0, and y = x^4. Use a graphing calculator or CAS to find the x-coordinates of the intersection points of the curves and to determine the area of the region D. Round your answers to six decimal places.
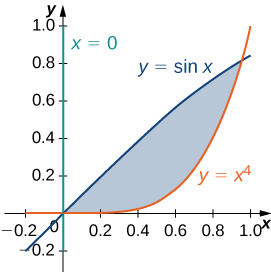
51) [T] The region D bounded by the curves y = \cos x, \space x = 0, and y = x^3 is shown in the following figure. Use a graphing calculator or CAS to find the x-coordinates of the intersection points of the curves and to determine the area of the region D. Round your answers to six decimal places.
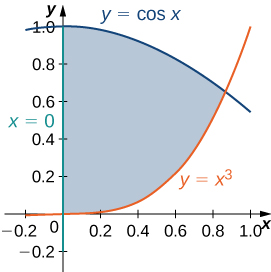
- Answer
- 0 and 0.865474; A(D) = 0.621135\, \text{units}^3
52) Suppose that (X,Y) is the outcome of an experiment that must occur in a particular region S in the xy-plane. In this context, the region S is called the sample space of the experiment and X and Y are random variables. If D is a region included in S, then the probability of (X,Y) being in D is defined as P[(X,Y) \in D] = \iint_D p(x,y)dx \space dy, where p(x,y) is the joint probability density of the experiment. Here, p(x,y) is a nonnegative function for which \iint_S p(x,y) dx \space dy = 1. Assume that a point (X,Y) is chosen arbitrarily in the square [0,3] \times [0,3] with the probability density
p(x,y) = \frac{1}{9} (x,y) \in [0,3] \times [0,3],\nonumber
p(x,y) = 0 \space \text{otherwise}\nonumber
Find the probability that the point (X,Y) is inside the unit square and interpret the result.
53) Consider X and Y two random variables of probability densities p_1(x) and p_2(x), respectively. The random variables X and Y are said to be independent if their joint density function is given by p_(x,y) = p_1(x)p_2(y). At a drive-thru restaurant, customers spend, on average, 3 minutes placing their orders and an additional 5 minutes paying for and picking up their meals. Assume that placing the order and paying for/picking up the meal are two independent events X and Y. If the waiting times are modeled by the exponential probability densities
p_1(x) = \frac{1}{3}e^{-x/3} \space x\geq 0,\nonumber
p_1(x) = 0 \space \text{otherwise}\nonumber
p_2(y) = \frac{1}{5} e^{-y/5} \space y \geq 0\nonumber
p_2(y) = 0 \space \text{otherwise}\nonumber
respectively, the probability that a customer will spend less than 6 minutes in the drive-thru line is given by P[X + Y \leq 6] = \iint_D p(x,y) dx \space dy, where D = \big\{(x,y)|x \geq 0, \space y \geq 0, \space x + y \leq 6\big\}. Find P[X + Y \leq 6] and interpret the result.
- Answer
- P[X + Y \leq 6] = 1 + \frac{3}{2e^2} - \frac{5}{e^{6/5}} \approx 0.45; there is a 45\% chance that a customer will spend 6 minutes in the drive-thru line.
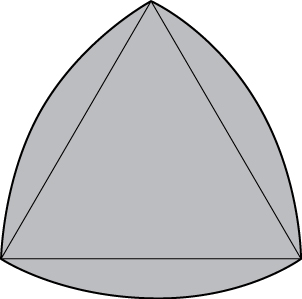
54) [T] The Reuleaux triangle consists of an equilateral triangle and three regions, each of them bounded by a side of the triangle and an arc of a circle of radius s centered at the opposite vertex of the triangle. Show that the area of the Reuleaux triangle in the following figure of side length s is \frac{s^2}{2}(\pi - \sqrt{3}).
55) [T] Show that the area of the lunes of Alhazen, the two blue lunes in the following figure, is the same as the area of the right triangle ABC. The outer boundaries of the lunes are semicircles of diameters AB and AC respectively, and the inner boundaries are formed by the circumcircle of the triangle ABC.