Iterated Integrals and Area (Exercises)

Last updated
Save as PDF

Page ID: 21139

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Terms and Concepts

1. When integrating $f_x(x,y)$ with respect to $x$, the constant of integration C is really which: $C(x)\text{ or }C(y)$? What does this mean?

Answer:: The constant of integration will be $C(y)$ since $y$ is considered a constant in the integration and thus, the original function $f$ could have terms that are functions of $y$ that were lost when taking the partial derivative with respect to the variable $x$.

2. Integrating an iterated integral is called _________ __________.

Answer:: iterated integration or multiple integration

3. When evaluating an iterated integral of the form $\displaystyle \int_a^b \int_{g_1(x)}^{g_2(x)}\,dy\,dx$, we integrate from _______ to ________, then from _________ to __________.

Answer:: We integrate from bottom to top, then from left to right. Here, from $y = g_1(x)$ to $y = g_2(x)$, then from $x = a$ to $x = b$.
More generally, we integrate from curve to curve and then from point to point.

4. One understanding of an iterated integral is that $\displaystyle \int_a^b \int_{g_1(x)}^{g_2(x)}\,dy\,dx$ gives the _______ of a plane region.

Answer:: area

Problems

In Exercises 5-10, evaluate the integral and subsequent iterated integral.

5. (a) $\displaystyle \int_2^5 (6x^2+4xy-3y^2)\,dy$
(b) $\displaystyle \int_{-3}^2 \int_2^5 (6x^2+4xy-3y^2)\,dy\,dx$

Answer:: (a) $\displaystyle \int_2^5 (6x^2+4xy-3y^2)\,dy$ $= \quad \left(6x^2y + 2xy^2 - y^3\right)\bigg|_2^5$ $= \quad 30x^2 + 50x - 125 - (12x^2 + 8x - 8)$ $=\quad 18x^2 +42x - 117$
(b) $\displaystyle \int_{-3}^2 \int_2^5 (6x^2+4xy-3y^2)\,dy\,dx$ $=\quad \displaystyle \int_{-3}^2 \left( 18x^2 +42x - 117 \right)\, dx$ $=\quad \left(6x^3 + 21x^2 -117x\right)\bigg|_{-3}^2$ $=\quad 48 + 84 - 234 - (-162 +189 +351)$ $=\quad -102 - 378$ $=\quad 480$

6. (a) $\displaystyle \int_0^\pi (2x\cos y +\sin x)\,dx$
(b) $\displaystyle \int_{0}^{\pi/2} \int_0^\pi (2x\cos y +\sin x)\,dx\,dy$

7. (a) $\displaystyle \int_1^x (x^2y-y+2)\,dy$
(b) $\displaystyle \int_0^2 \int_1^x (x^2y-y+2)\,dy\,dx$

Answer:: (a) $\displaystyle \int_1^x (x^2y-y+2)\,dy$ $= \quad \left(\frac{x^2y^2}{2} - \frac{y^2}{2} + 2y\right)\bigg|_1^x$ $= \quad \frac{x^4}{2} - \frac{x^2}{2} + 2x - (\frac{x^2}{2} - \frac{1}{2} + 2)$ $=\quad \frac{x^4}{2} - x^2 + 2x - \frac{3}{2}$
(b) $\displaystyle \int_0^2 \int_1^x (x^2y-y+2)\,dy\,dx$ $=\quad \displaystyle \int_{0}^2 \left( \frac{x^4}{2} - x^2 + 2x - \frac{3}{2} \right)\, dx$ $=\quad \left(\frac{x^5}{10} - \frac{x^3}{3} + x^2 - \frac{3}{2}x\right)\bigg|_{0}^2$ $=\quad \frac{32}{10} - \frac{8}{3} + 4 - 3 - 0$ $=\quad \frac{96}{30} - \frac{80}{30} + \frac{30}{30}$ $=\quad \dfrac{23}{15}$

8. (a) $\displaystyle \int_y^{y^2} (x-y)\,dx$
(b) $\displaystyle \int_{-1}^1 \int_y^{y^2} (x-y)\,dx\,dy$

9. (a) $\displaystyle \int_0^{y} (\cos x \sin y)\,dx$
(b) $\displaystyle \int_0^{\pi} \int_0^{y} (\cos x \sin y)\,dx\,dy$

Answer:: (a) $\displaystyle \int_0^{y} (\cos x \sin y)\,dx\quad$ $= \quad \left(\sin x \sin y \right)\bigg|_0^y$ $= \quad \sin^2 y$
(b) $\displaystyle \int_0^{\pi} \int_0^{y} (\cos x \sin y)\,dx\,dy\quad$ $=\quad \displaystyle \int_{0}^{\pi} \sin^2 y \, dy\quad$ $=\quad \displaystyle \int_{0}^{\pi} \frac{1-\cos 2y}{2}\, dy\quad$ $=\quad \dfrac{y - \frac{1}{2}\sin 2y}{2}\bigg|_{0}^{\pi}\quad$ $=\quad \frac{\pi}{2} - 0\quad$ $=\quad \dfrac{\pi}{2}$

10. (a) $\displaystyle \int_0^{x} \left (\frac{1}{1+x^2}\right )\,dy$
(b) $\displaystyle \int_1^2 \int_0^{x} \left (\frac{1}{1+x^2}\right )\,dy\,dx$

In Exercises 11-16, a graph of a planar region $R$ is given. Give the iterated integrals, with both orders of integration $dy\,dx$ and $dx\,dy$, that give the area of $R$. Evaluate one of the iterated integrals to find the area.

11.
$13111.PNG$

Answer:: $\text{Area} = \displaystyle \int_1^4 \int_{-2}^1 1\,dy\,dx\quad$ $=\quad \displaystyle \int_{-2}^1 \int_1^4 1\,dx\,dy$
$\displaystyle \int_{-2}^1 \int_1^4 1\,dx\,dy\quad$ $=\quad \displaystyle \int_{-2}^1 x\bigg|_1^4 \,dy\quad$ $=\quad \displaystyle \int_{-2}^1 3 \,dy\quad$ $=\quad 3y\bigg|_{-2}^1 \quad$ $=\quad 3(3) \quad$ $=\quad 9 \,\text{units}^2$

12.
$13112.PNG$

13.
$13113.PNG$

Answer:: $ \text{Area} = \displaystyle \int_2^4 \int_{x-1}^{7-x} 1\,dy\,dx\quad$ $=\quad \displaystyle \int_{1}^3 \int_{2}^{y+1} 1\,dx\,dy\quad + \quad \displaystyle \int_{3}^5 \int_{2}^{7-y} 1\,dx\,dy\quad$
$\displaystyle \int_2^4 \int_{x-1}^{7-x} 1\,dy\,dx\quad$ $=\quad\displaystyle \int_2^4 y\bigg|_{x-1}^{7-x}\,dx\quad$ $=\quad\displaystyle\int_2^4 (8 - 2x)\,dx\quad$ $=\quad(8x - x^2)\bigg|_2^4 = 32 - 16 - 16 + 4 \quad$ $=\quad 4 \,\text{units}^2$

14.
$13114.PNG$

15.
$13115.PNG$

Answer:: $ \text{Area} = \displaystyle \int_0^1 \int_{x^4}^{\sqrt{x}} 1\,dy\,dx\quad$ $=\quad \displaystyle \int_{0}^1 \int_{y^2}^{\sqrt[4]{y}} 1\,dx\,dy\quad$
$ \displaystyle \int_0^1 \int_{x^4}^{\sqrt{x}} \,dy\,dx\quad$ $=\quad\displaystyle \int_0^1 y\bigg|_{x^4}^{\sqrt{x}}\,dx\quad$ $=\quad\displaystyle\int_0^1 (\sqrt{x} - x^4)\,dx\quad$ $=\quad(\frac{2}{3}x^{3/2} - \frac{x^5}{5})\bigg|_0^1 \quad$ $=\quad \frac{2}{3} - \frac{1}{5} \quad$ $=\quad \frac{10}{15} - \frac{3}{15} $ $=\quad \dfrac{7}{15} \,\text{units}^2$

16.
$13116.PNG$

In Exercises 17-22, iterated integrals are given that compute the area of a region R in the $xy$-plane. Sketch the region R, and give the iterated integral(s) that give the area of R with the opposite order of integration.

17. $\displaystyle \int_{-2}^2 \int_0^{4-x^2}\,dy\,dx$

Answer:: $\displaystyle \int_{-2}^2 \int_0^{4-x^2}\,dy\,dx\quad$ $=\quad \displaystyle \int_{0}^4 \int_{-\sqrt{4-y}}^{\sqrt{4-y}}\,dx\,dy$
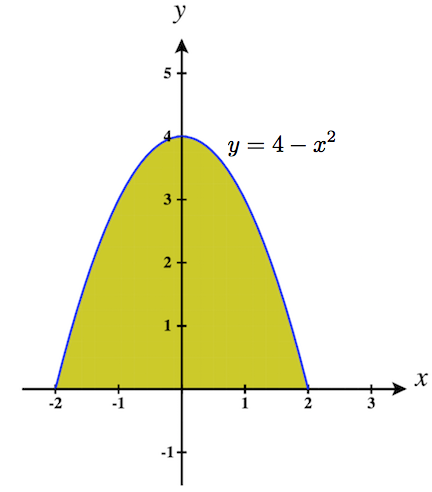
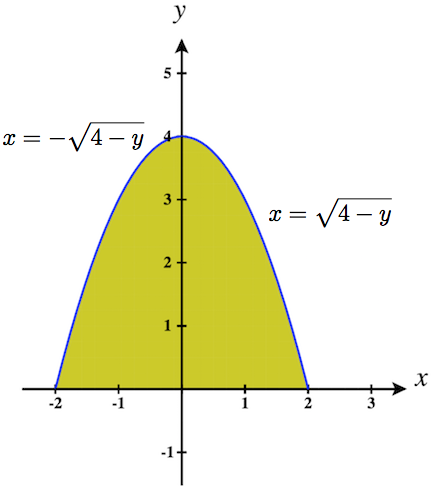
$Figure14-1-Ex19a.png$ $Figure14-1-Ex19b.png$

18. $\displaystyle \int_{0}^1 \int_{5-5x}^{5-5x^2}\,dy\,dx$

19. $\displaystyle \int_{-2}^2 \int_0^{2\sqrt{4-y^2}}\,dx\,dy$

Answer:: $\displaystyle \int_{-2}^2 \int_0^{2\sqrt{4-y^2}}\,dx\,dy\quad$ $=\quad \displaystyle \int_{0}^4 \int_{-\frac{1}{2}\sqrt{16-x^2}}^{\frac{1}{2}\sqrt{16-x^2}}\,dy\,dx$
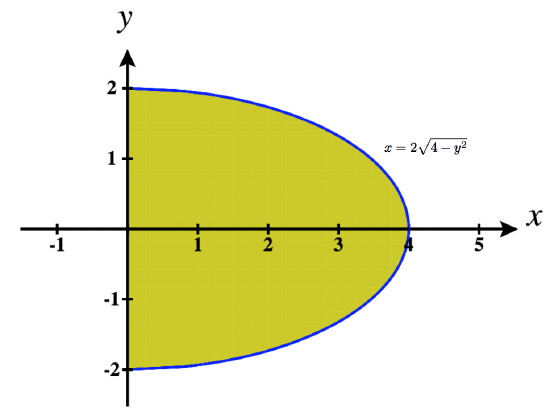
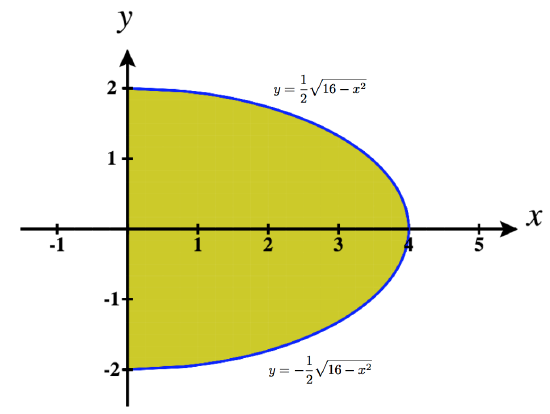
$Fig14-1-Ex19a.png$ $Fig14-1-Ex19b.png$

20. $\displaystyle \int_{-3}^3 \int_{-\sqrt{9-x^2}}^{\sqrt{9-x^2}}\,dy\,dx$

21. $\displaystyle \int_{0}^1 \int_{-\sqrt{y}}^{\sqrt{y}}\,dx\,dy +\int_1^4 \int_{y-2}^{\sqrt{y}}\,dx\,dy$

Answer:: $\displaystyle \int_{0}^1 \int_{-\sqrt{y}}^{\sqrt{y}}\,dx\,dy +\int_1^4 \int_{y-2}^{\sqrt{y}}\,dx\,dy \quad$ $=\quad \displaystyle \int_{-1}^2 \int_{x^2}^{x+2}\,dy\,dx$
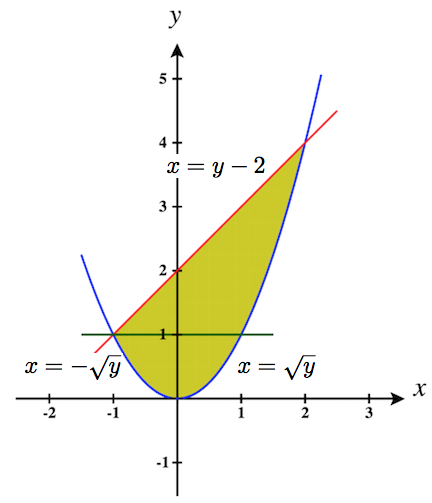
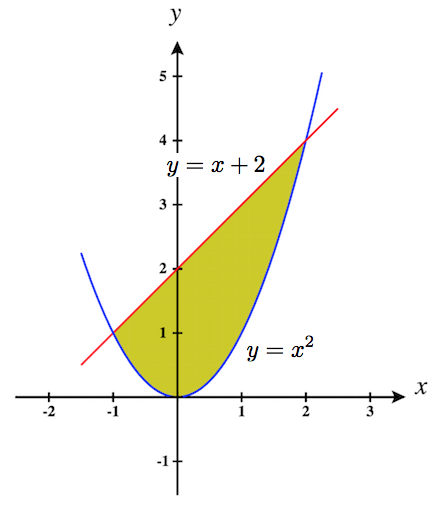
$Figure14-1-Ex21a.png$ $Figure14-1-Ex21b.png$

22. $\displaystyle \int_{-1}^1 \int_{(x-1)/2}^{(1-x)/2}\,dy\,dx$