3.1: Symmetric Groups

Definition: Symmetric Group

Let \(n\in \mathbb{N}\). Let \(X=\{1,\ldots,n\}\), be a set. Then \(S_n\) is the set of all the bijections from \(X\) to \(X\) (permutations). Note that there are \(n!\) permutations. The operation \(\star : = \) composition of bijections.  Note that it is a right-to-left composition.

Figure \(\PageIndex{1}\): composition of bijections. (Copyright: Pamini Thangarajah)

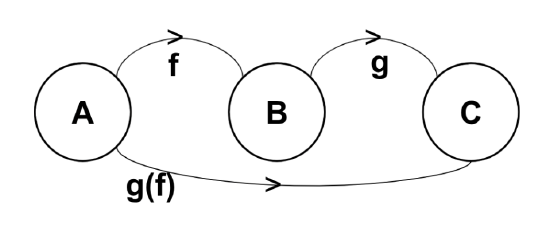
\(S_n\) with compositions forms a group; this group is called a Symmetric group. \(S_n\) is a finite group of order \(n!\) and are permutation groups consisting of all possible permutations of n objects.

Identity permutation is denoted as \(e\).

We will denote a permutation by \(\sigma = \begin{bmatrix} 1 & 2& 3& \cdots & n\\
\sigma(1) & \sigma(2) & \sigma(3) & \cdots & \sigma(n) \end{bmatrix} \in S_n\)

 

Example \(\PageIndex{1}\)

Let \(\sigma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
2 & 4 & 3 & 5 & 1 \end{bmatrix} \in S_5\) and

\( \gamma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 4 & 1 & 2 & 3 \end{bmatrix} \in S_5 \).

Lets find \(\gamma \circ \sigma\).

Figure \(\PageIndex{2}\): \(\gamma \circ \sigma\). (Copyright; Pamini Thangarajah via Google draw)

Figure \(\PageIndex{2}\) illustrates the process of moving from one function to another.  Note the system is closed since it is a bijection. Completing the process, we obtain the following: 

Consider \(\gamma \circ \sigma = \gamma \sigma =\) \(\begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 4 & 1 & 2 & 3 \end{bmatrix}  \begin{bmatrix} 1 & 2& 3& 4 & 5\\
2 & 4 & 3 & 5 & 1 \end{bmatrix}= \begin{bmatrix} 1 & 2& 3& 4 & 5\\
4 & 2 & 1 & 3 & 5 \end{bmatrix} \)

Note, if we switch the order of the functions are switched, we obtain: \(\sigma \gamma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
1 & 5 & 2 & 4 & 3 \end{bmatrix}\).

Note that \(\sigma \gamma \ne \gamma \sigma\).  To prove not abelian, we need only show that for at least one element, \(k\), \(\sigma \gamma(k) \ne \gamma \sigma(k)\).

Note

The inverse of a permutation \(\sigma\) is the inverse of the function \(\sigma\), and it is denoted by  \(\sigma^{-1}\).

Thus,  \(\sigma^{-1} \sigma=\sigma \sigma^{-1}=e.\)

Example \(\PageIndex{2}\)

Let \(\sigma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
2 & 4 & 3 & 5 & 1 \end{bmatrix} \in S_5\). Then  Let \(\sigma^{-1} = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 1 & 3 & 2 & 4 \end{bmatrix} \in S_5\).

Cycle Notation

Cycle notation, a simple and straightforward method, is a convenient way to represent permutations in the symmetric group. For example:

Example \(\PageIndex{3}\)

Let \(\gamma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 4 & 1 & 2 & 3 \end{bmatrix}=(1,5,3)(2,4)\).

Figure \(\PageIndex{3}\): \(\gamma\). (Copyright: Pamini Thangarajah )

\((1,5,3)\) can be read as 1 goes to 5, 5 goes to 3, and 3 goes back to 1, and is called a cycle of  \(\gamma\) of length \(3\). Then 2 goes to 4, and then 4 goes back to 2, and \((2,4)\) is called a cycle of  \(\gamma\) of length \(2\).

Note

•  \((1,2,4,5)\) means that 1 goes to 2, 2 goes to 4, 4 goes to 5 and 5 goes to 1.  Note that 3 is not included, so 3 goes to 3. 
• There is no cycle notation in the case of the identity, \(e\), and we use \(e\).  

• The cycles are always listed in a logical and clear order-descending order of their smallest element.

• If the permutation fixes an element (i.e., it remains unchanged), it is often omitted from the cycle notation.

Definition: Cycle

A cycle \(\gamma=(a_1,\ldots,a_k)\) means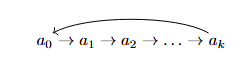 

 

Definition: disjoint cycles

Disjoint cycles mean that the elements involved in one cycle are distinct from those in another. 

Two cycles in \(S_n\), \(\gamma=(a_1,\ldots,a_k)\) and \(\sigma=(b_1,\ldots,b_l)\) are disjoint if \(a_i \ne b_j, \; \forall i,j\).

Note that the length of the cycles does not need to be the same. 

Example:  \((1, 2)\) and \((3, 4)\) are disjoint, but \((1, 2, 3)\) and \((3, 4)\) are not disjoint.

Example \(\PageIndex{4}\)

Let \( \sigma = \begin{bmatrix} 1 & 2& 3& 4 & 5& 6 & 7 & 8 & 9 &10 &11&12\\
12 & 2 & 3 & 1 & 11 & 9 & 5 &10 & 6 &4& 7 & 8 \end{bmatrix} \)

Then, a cycle decomposition of 

  \( \sigma = (1, 12, 8, 10, 4) (2)(3)(5,11,7)(6,9)= (1, 12, 8, 10, 4) (5,11,7)(6,9) \).

Note that these are disjoint cycles; therefore, they commute.

Theorem \(\PageIndex{1}\)

1. Disjoint cycles are commutative.

Let \(\gamma\) and \(\sigma\) be disjoint cycles, then \(\gamma \sigma = \sigma \gamma\).

2. Every permutation of a finite set can be written as a cycle or a product of disjoint cycles.

The inverse of a cycle:

Theorem \(\PageIndex{2}\)

\((a_1, a_2, \cdots, a_k)^{-1}= (a_k, a_{k-1}, \cdots, a_1)\)

Example \(\PageIndex{5}\)

\( (1,2,3)^{-1} = (3,2,1) \), and \((1,2)^{-1}=(2,1)=(1,2).\) 

Let \( \sigma = \begin{bmatrix} 1 & 2& 3& 4 & 5& 6 & 7 & 8 & 9 &10 &11&12\\
12 & 2 & 3 & 1 & 11 & 9 & 5 &10 & 6 &4& 7 & 8 \end{bmatrix} = (1, 12, 8, 10, 4) (5,11,7)(6,9). \)

In a cycle decomposition, to find the inverse, just reverse the order of the cycles and find the inverse of each cycle. Hence, 

 \( \sigma^{-1} =(6,9)^{-1}(5, 11, 7)^{-1} (1, 12, 8, 10, 4)^{-1}=(9,6)(7, 11, 5) (4, 10, 8, 12, 1)  \)

Note that disjoint cycles are commutative!

Caution

\((2,3)(1,2) = (1,3,2) =(3,2,1)=(2,1,3)\) Note:  1 goes to 2 first, then to 2 and then gets to  3.

\((1,2)(2,3)= (1,2,3)=(2,3,1)=(3,1,2)\)  Note: Since there is no 1 in the inner function, it goes to itself and then goes to 2.

Type of a permutation (cycle structure of a permutation)

The type of a permutation (or cycle structure of a permutation) is the integer partition formed from the cycle lengths in decreasing order. We will denote it by type(\(\sigma \)), where \(\sigma \) is a permutation in \(S_n\).

Example \(\PageIndex{6}\)

Let \(\gamma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 4 & 1 & 2 & 3 \end{bmatrix}=(1,5,3)(2,4) \in S_5\).

The type of \(\gamma\) is,  type \( (\gamma)=\)3 2.

 

Example \(\PageIndex{7}\)

Let \(\sigma = \begin{bmatrix} 1 & 2& 3& 4 \\
 4 & 1 & 2 & 3 \end{bmatrix}=(1,4,3,2) \in S_4\).

The type \( \sigma\) is, type \( (\sigma)=\)4.

Note

A partition of a positive integer \(n\)   is a sum of nonnegative integers \(n=k_1+\cdots+k_s, k_i \in \mathbb{N},\) where the order of the summand is not important. For example: 

The partitions of \(6\) are \(6, 5+1, 4+2, 4+1+1 , 3+3, 3+2+1, 3+1+1+1, 2+2+2, 2+2+1+1, 2+1+1+1+1, 1+1+1+1+1+1.\)

Example \(\PageIndex{8}\)

How many permutations in \(S_6\) have type 321?

Type \((321)\) permutation is of the form \( (_,_,_)(_,_)(_) \). There are \(6!\) ways of filling the blanks. Note that each cycle can be restarted anywhere.

Hence, the number of permutations in \(S_6\) have type (321) is \(\dfrac{6!}{(3)(2)(1)}.\)

Example \(\PageIndex{9}\)

How many permutations in \(S_6\) have  \(3\) cycles of length \(2\)?

The  permutation is of the form \( (_,_)(_,_)(_,_) \). There are \(6!\) ways of filling the blanks.  Since each cycle has two representations matching this format (by restarting at any two places), so divided by \(2^3\).

The order of the whole cycle can be changed while keeping the pattern. Divide by \(3!\) ways to reorder the cycles.

Hence, the number of permutations in \(S_6\) have  \(3\) cycles of length \(2\) is \(\dfrac{6!}{(2^3)(3!)}.\)

Theorem \(\PageIndex{3}\)

Suppose the number of cycles of length \(i\) is \(m_i\), for \(i=1, \cdots, k.\) and \(n=m_1+2m_2+\cdots+(k-1)m_{(k-1)}+ km_k.\)

The number of  permutations in \(S_n\) of the type \((m_k m_{(k-1)} \cdots m_1)\)  is 

\(\dfrac{n!}{1^{m_1}2^{m_2}\cdots k^{m_k} {m_1}! m_2! \cdots m_k!}.\)

Example \(\PageIndex{10}\)

 \(|S_3|=3!=2\cdot 3=6\).

Table \(\PageIndex{1}\): Cycle type for \(S_3\)
Cycle type	111	21	3
Number of permutations	\(\dfrac{3!}{1^3 3!}=1\)	\(\dfrac{3!}{1^1 2^1 1!1!}=3\)	\(\dfrac{3!}{ 3^1 1!1!}=2\)

Notation: 

         \(1 \equiv \begin{pmatrix}
1 & 2 & 3\\
1 & 2 & 3
\end{pmatrix}\) the identity matrix.

   \((1,2) \equiv \begin{pmatrix}
1 & 2 & 3\\
2 & 1 & 3
\end{pmatrix}\).  Note that 3 points to itself.

\((1,2,3) \equiv \begin{pmatrix}
1 & 2 & 3\\
2 & 3 & 1
\end{pmatrix}\).

\((1,3,2) \equiv \begin{pmatrix}
1 & 3 & 2\\
3 & 2 & 1
\end{pmatrix}\).

Hence, \(S_3= \{e,(1,2),(1,3), (2,3), (1,2,3),(1,3,2)\}\).   

 

Table \(\PageIndex{2}\): Cayley table for \(S_3\)
	e	(1,2,3)	(1,3)	(1,2)	(2,3)	(1,3,2)
e	e	(1,2,3)	(1,3)	(1,2)	(2,3)	(1,3,2)
(1,2,3)	(1,2,3)	(1,3,2)	(2,3)	(1,3)	(1,2)	e
(1,3)	(1,3)	(1,2)	e	(1,2,3)	(1,3,2)	(2,3)
(1,2)	(1,2)	(2,3)	(1,3,2)	e	(1,2,3)	(1,3)
(2,3)	(2,3)	(1,3)	(1,2,3)	(1,3,2)	e	(1,2)
(1,3,2)	(1,3,2)	e	(1,2)	(2,3)	(1,3)	(1,2,3)

 

Example \(\PageIndex{11}\)

Let's explore \(S_4\). Note \(S_4\) has  \(4!=24\) elements.

 

Table \(\PageIndex{3}\): Cycle type for \(S_4\)
Cycle type	1111	211	22	31	4
Number of permutations	\(\dfrac{4!}{1^4 4!}=1\)	\(\dfrac{4!}{1^2 2^1 2!1!}=6\)	\(\dfrac{4!}{ 2^2 2!}=3\)	\(\dfrac{4!}{1^1 3^1 1!1!}=8\)	\(\dfrac{4!}{4^1  1!}=6\)

 

Hence, \[S_4=\{e, (1,2), (1,3), (1,4), (2,3), (2,4), (3,4),(1,2)(3,4), (1,3)(2,4), (1,4)(2,3), (1,2,3), (1,3,2), (2,3,4), (2,4,3), (3,4,1), (3,1,4), (4,1,2), (4,2,1),(1,2,3,4), (1,2,4,3), (1,3,4,2), (1,3,2,4), (1,4,2,3), (1,4,3,2) \}. \]

Note

Notice that all the elements in \(S_3\) in \(S_4\).

 

The following theorem proves that \(S_n\) are non-Abelian for integer n ≥ 3, which means that the order in which we compose permutations matters. 

Theorem \(\PageIndex{4}\)

\(S_n\) is non-Abelian for all integers n ≥ 3.

Proof

Let \(a,b \in S_3\).

We will show that there exists  \(a, b \in S_n, s.t.  ab \ne ba \), \(n \ge 3\).

Note \(S_3=\{e,(1,2),(1,3),(2,3),(1,2,3),(1,3,2)\}\).

Let \(a=(1,2)\) and \(b=(2,3)\) both elements of \(S_3\).

Consider \(ab=(1,2)(1,3)=(1,3,2)\) and \(ba=(1,3)(1,2)=(1,2,3)\).

Since \((1,3,2) \ne (1,2,3)\), \(ab\ne ba \; \forall a,b \in S_3\), thus \(S_3\) is non-abelian.

Since \(a,b \le S_n, \; \forall n \ge 3\), \(S_n\) in non-abelian for \(n\ge 3\).◻

 

Example \(\PageIndex{12}\)

Given \(\alpha, \beta \in S_4\) with \(\alpha \beta =(1,4,3,2), \; \beta \alpha = (1,2,4,3)\), and \(\alpha(1)=4\), determine \(\alpha\) and \(\beta\).

Solution:

Let \(\alpha=(1,4,c,d)\) and \(\beta=(w,x,y,z)\).

Since \(\alpha(1)=4\) and \(\beta \alpha(1)=2\), implies \(\beta(4)=2\).

Since \(\beta(4)=2\) and \(\alpha \beta(4)=3\), implies \(\alpha(2)=3\).

Since \(\alpha(2)=3\) and \(\beta \alpha(2)=4\), implies \(\beta(3)=4\).

Since \(\beta(3)=4\) and \(\alpha \beta(3)=2\), implies \(\alpha(4)=2\).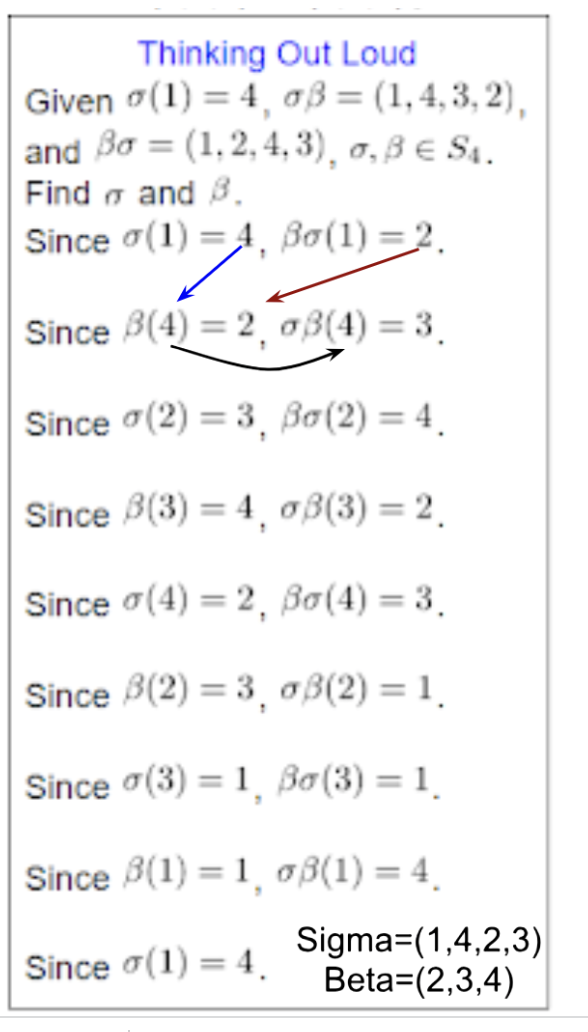

Since \(\alpha(4)=2\) and \(\beta \alpha(4)=3\), implies \(\beta(2)=3\).

Since \(\beta(2)=3\) and \(\alpha \beta(2)=1\), implies \(\alpha(3)=1\).

Since \(\alpha(3)=1\) and \(\beta \alpha(3)=1\), implies \(\beta(1)=1\).

\(\alpha=(1,4,2,3)\) and \(\beta=(2,3,4)\).

Then \(\beta \alpha =(2,3,4)(1,4,2,3)=(2,4,3,1)=(1,2,4,3)\).

And \(\alpha \beta =(1,4,2,3)(2,3,4)=(4,3,2,1)=(1,4,3,2)\).

Figure \(\PageIndex{4}\): Thinking out Loud (Copyright: Pamini Thangarajah)

 

 

Note that every permutation of a finite set can be written as a cycle or a product of disjoint cycles.

2 Cycle (Transposition)

 

Definition: Transposition

\((i,j), \; i\le j, \; j\le n, \; i \ne j\).

\((i,j)^{-1}=(j,i)=(i,j)\).

Example \(\PageIndex{1}\)

(1, 3, 2) = (1, 2) (1, 3)  1 goes to 3, 3 goes to itself, then to 1 then to 2.

(1, 2, 3) = (1, 3) (1, 2).

(2, 4, 1, 3, 5) = (2, 5) (2, 3) (2, 1) (2, 4)

Note:  Any cycle can be written as a composition of two cycles.

Theorem \(\PageIndex{5}\)

A \(k-\)cycle \( (i_1,i_2\cdots, i_k) \) can be decomposed into a product of \(k-1\) transpositions. That is,

\( (i_1,i_2\cdots, i_k)=(i_1,i_k)(i_1, i_{k-1})\cdots (i_1,i_2). \) 

Theorem \(\PageIndex{6}\)

Every permutation in \(S_n\) can be expressed as a product of 2-cycles (Transpositions). The number of transpositions will either always be even or odd.

If a permutation α can be expressed as a product of an even number of 2-cycles, then every decomposition of α into a product of 2-cycles has an even number of 2-cycles.  A similar statement holds for odd.
 

Permutation parity 

Definition: Parity

Let \(\sigma \in S_n\).  (i.e. a permutation)

Then 

(1) \(\sigma\) is an even permutation if \(\sigma\) can be expressed as a product of an even number of two cycles (transpositions).

(2) \(\sigma\) is an odd permutation if \(\sigma\) can be expressed as a product of an odd number of two cycles (transpositions).

Theorem \(\PageIndex{7}\)

1. A cycle of even length is odd.

2. A cycle of odd length is even.

 

Example \(\PageIndex{13}\)

1. let’s explore \(S_4\). Note \(S_4\) has  \(4!=24\) elements.

Consider \(S_4=\{e, (1,2), (1,3), (1,4), (2,3), (2,4), (3,4),(1,2)(3,4), (1,3)(2,4), (1,4)(2,3), (1,2,3),(1,3,2), (2,3,4), (2,4,3), (3,4,1), (3,1,4), (4,1,2), (4,2,1),(1,2,3,4), (1,2,4,3), (1,3,4,2), (1,3,2,4), (1,4,2,3), (1,4,3,2) \}\) 

 

2. Find the center of \(S_4\).

Since all symmetrical groups, \(S_n\),  \(n \ge 3\), are non-abelian, the centre of \(S_4\) is trivial, being the identity e, or (1)(2)(3)(4). (what do you think of this proof? Is this a valid argument?)

Alternatively, proof by exhaustion:  Having tried all \(x \in S_4\), the only \( x \in S_4\) that satisfies \(xg=gx, \; \forall g \in S_4\) is the identity.

 

3. Find the cyclic subgroup of \(S_4\) that has an order of 4.  

The subgroup of \(S_4, C4 =\{e, (1,2,3,4),(1,3)(2,4),(1,4,3,2) \}\), has an order 4 and is generated by \((1,2,3,4)\). 

\((1,2,3,4)^2=(1,3)(2,4)\), \((1,2,3,4)^3=(1,4,3,2)\), and \((1,2,3,4)^4=e\).

 

4. Find a non-cyclic subgroup of \(S_4\) that has order 4.

The 2-2 cycles together will form an order 4 group. 

\(\{e, (1,2)(3,4),(1,3)(2,4),(1,4)(2,3)\}\) is a subgroup of \(S_4\) and has order 4.  Note the inverse of \((1,2)(3,4)\) is \((4,3)(2,1)\), which is \((1,2)(3,4)\).  Since a similar argument can be made for the other 2-2 cycles, the inverses of each element exist.  In addition, the set is closed under composition.

Theorem \(\PageIndex{8}\)

The center of \(S_4, Z(S_4)=\{e\}.\)

Proof

Proof by contradiction

Let \(\gamma (\ne e) \in Z(S_n).\)  We shall find an \(\alpha \in S_n\) such that \(\gamma \alpha \ne \alpha \gamma.\) Since \(\gamma (\ne e)\), there exist \(l,m \in \{1,2,3,\cdots, n\}\) such that  \(\gamma (l) =m \ne l.\) Now we can choose an element \(k \in \{1,2,3,\cdots, n\}\) such that \(k\ne l\) and \(k\ne m\). Choose \(\alpha=(l,k).\) Then \(\gamma \alpha(l)=\gamma(k)\) and \( \alpha \gamma (l)= \alpha(m)=m\). Since \(\gamma\) is a bijection and  \(\gamma (l) =m \ne l\), \(\gamma(k) \ne m\).  This is a contradiction. Hence, \(Z(S_n) = \{e\}\).

 

Order of a permutation

Let \(\sigma=(1, 2, 3)\).

Then \(\sigma^2=(1, 2, 3)(1, 2, 3)=(1, 3, 2)=\sigma^{-1}\).

Further \(\sigma ^3=(1, 2, 3)(1, 3, 2)=(1)(2)(3)=e\).  We shall refer to \(e\) as 1.

Thus the order of \(\sigma\), \(|\sigma |=3\).

Theorem \(\PageIndex{9}\)

If \(\sigma=(a_1, \ldots, a_k)\), then the \(|\sigma |=k\). 

Proof

 Since \(\sigma^k(a_i)=a_i, \forall i=1, cdots, n, \sigma^=(a_1, \ldots, a_k)^k=e.\)  We shall show that \(k\) the smallest positive integer such that \(\sigma^k=e.\) Suppose \( m\) is a positive integer such that \(0 < m<k.) Then \(\sigma^m(a_i)=a_{i+m} \ne a_i\, \forall i=1, cdots, n). Hence \(k\) the smallest positive integer such that \(\sigma^k=e.\)

Example \(\PageIndex{14}\)

 Let \(\gamma = (1, 2, 4)\). Then

\(\gamma^2=(1, 2, 4)(1,2, 4)=(1, 4, 2)\).

\(\gamma^3=(1, 2, 4)(1, 4, 2)=(1)(2)(4)=e\).

 

Theorem \(\PageIndex{10}\)

The order of a permutation of a finite set, written in disjoint cycle form, is the least common multiple of the lengths of the cycles.

Example \(\PageIndex{15}\)

Find the orders of the 5040 elements of \(S_7.\)

Solution

The longest cycle in \(S_7\) is the one that includes all the elements -- 7. We will show cycle lengths as \(\underline{7}\).  Note the underlining.  The possible cycles are shown in the table below.  Note that the leading term is the longest cycle in the permutation.

Cycle type	Order	Cycle type	Order	Cycle type	Order
7	7	4 2 1	4	3 1 1 1 1	3
6 1	6	4 1 1 1	4	2 2 2 1	2
5 2	10	3 3 1	3	2 2 1 1 1	2
5 1 1	5	3 2 2	6	2 1 1 1 1 1	2
4 3	12	3 2 1 1	6	1 1 1 1 1 1 1	1

Conjugacy classes of \(S_n\)

Recall:

Two elements \(x,y \) in a group \(G\) are conjugate if \(y=gxg^{-1}\) for some \(g\in G\).

Theorem \(\PageIndex{11}\)

For \(\alpha , \beta \in S_n\text{,}\) define \(\alpha \sim \beta\) if there exists a \(\sigma \in S_n\) such that \(\sigma \alpha \sigma^{-1} = \beta\text{.}\) Then \(\sim\) is an equivalence relation on \(S_n\text{.}\)

Proof

Reflexive: Let \(\alpha \in S_n\). Then \( e\in S_n\) and \(e \alpha e^{-1} = \alpha\text{.}\) Hence  \(\alpha \sim \alpha\). Thus \(\sim\) is reflexive on \(S_n\text{.}\)

Symmetric: Let \(\alpha , \beta \in S_n\) such that \(\alpha \sim \beta\). Then there exists a \(\sigma \in S_n\) such that \(\sigma \alpha \sigma^{-1} = \beta\text{.}\)  Therefore,  \(\sigma^{-1} \beta \sigma= \alpha\text{,}\)  and \(\sigma^{-1} \in S_n\).  Hence, \(\beta \sim \alpha\). Thus \(\sim\) is symmetric on \(S_n\text{.}\)

Transitive: Let \(\alpha , \beta , \gamma \in S_n\) such that \(\alpha \sim \beta\) and  \(\beta \sim \gamma\). Then there exist \(\sigma_1, \sigma_2 \in S_n\) such that \(\sigma_1 \alpha \sigma_1^{-1} = \beta\text{,}\) and  \(\sigma_2\beta \sigma_2^{-1}= \gamma\text{.}\) Consider, \begin{align*} \gamma &= \sigma_2\beta \sigma_2^{-1}\\ &= \sigma_2 \left( \sigma_1 \alpha \sigma_1^{-1}  \right) \sigma_2^{-1}\\ &=\left( \sigma_2 \sigma_1\right) \alpha \left( \sigma_1^{-1}   \sigma_2^{-1}\right)\\  &= \left( \sigma_2 \sigma_1\right) \alpha \left( \sigma_2  \sigma_1\right)^{-1} .\end{align*} Hence,  \(\alpha \sim \gamma\).  Thus \(\sim\) is transitive on \(S_n\text{.}\)

Since \(\sim\) is reflexive, symmetric and transitive, \(\sim\) is an equivalence relation on \(S_n\text{.}\)

The equivalence classes are called conjugacy classes of \(G\), subsets of \(G\) in which elements are conjugate to each other.

Theorem \(\PageIndex{12}\)

Two permutations in \(S_n\) are conjugate if and only if they have the same cycle structure, i.e. they have the same cycle type.

Example \(\PageIndex{16}\)

Conjugacy classes of \(S_3.\)

Solution

There are three conjugacy classes. Those are \( \{(1,2),(2,3),(1,3)\},\{e\},\{(1,2,3),(3,2,1)\}.\)