0.3: Trigonometry
- Page ID
- 10823
The right triangle
Trigonometric functions
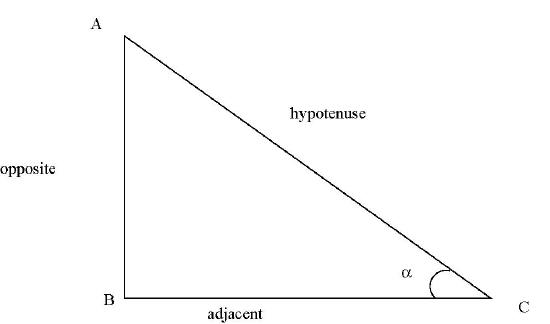
Usually in a triangle when there is no chance of ambiguity, the sides opposite to each vertex have length denoted by the corresponding small letter.
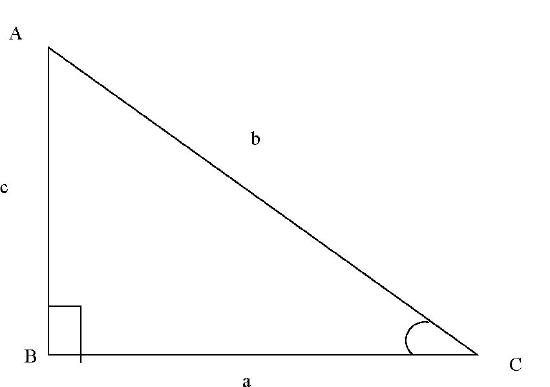
In the diagram, the triangle \(ABC\) has a right angle at \(B.\)
\[\sin (A)= \frac{\mbox {length of the opposite side}}{ \mbox{ length of the hypotenuse}}=\frac{a}{b}.\]
\[\cos (A)= \frac{\mbox {length of the adjacent side}}{ \mbox{ length of the hypotenuse}}=\frac{c}{b}.\]
\[\tan (A)= \frac{\mbox {length of the opposite side}}{ \mbox{ length of the length of the adjacent side}} =\frac{a}{c}= \frac{\sin (A)}{\cos (A)}.\]
The remanining functions can be considered to be reciprocal functions.
\[\csc (A)=\frac{1}{\sin (A)},\]
\[\sec (A)=\frac{1}{\cos (A)},\]
\[\cot (A)=\frac{1}{\tan (A)}.\]
Solving the general triangle
Rules
Consider the triangle \(ABC\) in the diagram:
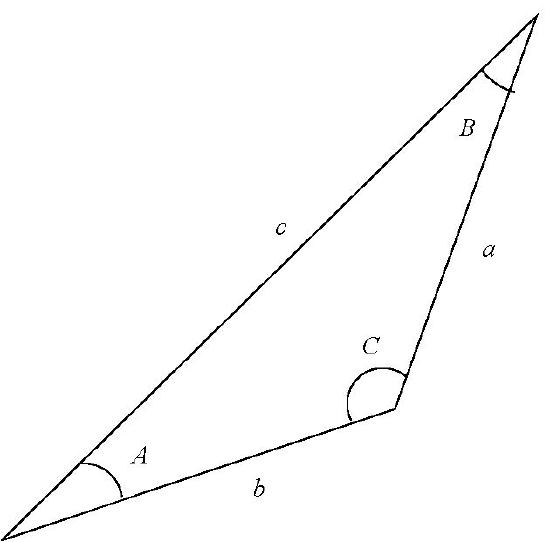
1. The sine law:
\[\frac{a}{ \sin (A)}=\frac{b}{ \sin (B)}=\frac{c}{ \sin (C)}\]
2. The cosine law:
\[a^2=b^2+c^2-2bc \cos (A)\] or equivalently,
\[ \cos (A)= \frac{b^2+c^2-a^2}{2bc}\]
3. The area of the triangle \(ABC\) is \(\frac{1}{2} bc \sin (A).\)
4. If the perimeter of the triangle \(= 2s= a+b+c,\) then \[\sin (A)= \frac{2}{bc} \sqrt{s(s-a)(s-b)(s-c)}\]
and the area of the triangle is \(\sqrt{s(s-a)(s-b)(s-c)}\).
Unit Circle
Definition
Unit circle is circle with center at the origin \((0,0)\) and radius \(1\).
Unit circle has the equation \(x^2+y^2=1.\)
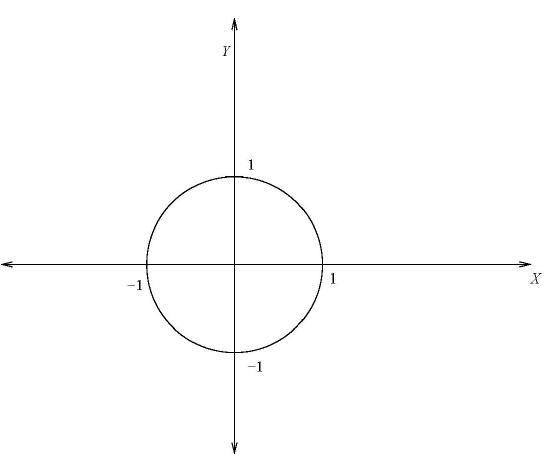
The radian measure of an angle is equal to the numerical value of the length of the arc of the unit circle from the point
\((1,0)\) to the point \((x,y).\)
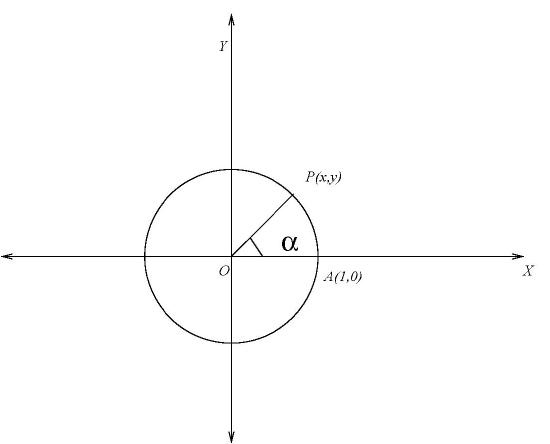
Thus, \(\mbox{length of the arc } AP=\alpha \mbox{ radian units}.\)
Hence we obtain the conversion from degrees to radians and vice-versa:\[\pi \,{\rm radians}=180^{\circ}\]
Definition of the trigonometric functions
There are two ways to define trigonometric functions:
Definition
Using triangles or circles.
1. The definition using triangles is too restrictive in that it treats only angles between \(0\) degree and \(90\) degrees.
2. The definition using circles, on the other hand, leads to a much more general definition, since the angle can now take on any real value whatsoever.
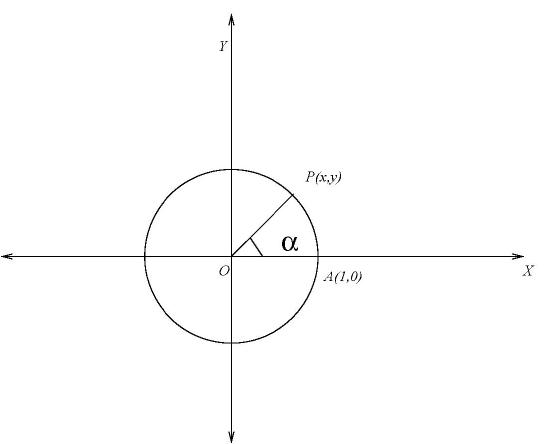
In the diagram above, \(A(1,0)\) is the fixed point from which measurements begin. Angles and arc lengths are measured from \(A\) in a counter-clockwise direction.
If \(P(x,y)\) is any point on the circumference of the unit circle, then if the arc length of \(AP= \alpha\) units, then \(\angle AOP = \alpha\) radians, we define \[\sin (\alpha)=x \mbox{ and} \cos (\alpha)=y.\]
Further, we define \[\tan (\alpha)=\frac{\sin (\alpha)}{\cos (\alpha)} \]
\[\cot (\alpha)=\frac{\cos (\alpha)}{\sin (\alpha)}, \]
\[\sec (\alpha)=\frac{1}{\cos (\alpha)}, \]
\[\csc (\alpha)=\frac{1}{\sin (\alpha)}. \]
Some important relationships on unit circle
Rules
\[\left.\begin{array}{c}
\sin (\pi- \alpha)=\sin (\alpha).\\
\cos (\pi- \alpha)=-\cos (\alpha).\\
\tan (\pi- \alpha)=-\tan (\alpha).
\end{array}
\right\} \mbox{ Quadrant II}\]
\[\left.\begin{array}{c}
\sin (\pi+\alpha)=-\sin (\alpha).\\
\cos (\pi+ \alpha)=-\cos (\alpha).\\
\tan (\pi+ \alpha)=\tan (\alpha).
\end{array}
\right\} \mbox{ Quadrant III}\]
\[\left.\begin{array}{c}
\sin (2\pi- \alpha))=\sin (-\alpha)=-\sin (\alpha).\\
\cos (2\pi- \alpha)=\cos (-\alpha=\cos (\alpha).\\
\tan (2\pi- \alpha)=\tan (-\alpha)=-\tan (\alpha).
\end{array}
\right\} \mbox{ Quadrant IV}\]
\[\sin (\pi/2-\alpha)=\cos (\alpha).\]
\[\cos (\pi/2-\alpha)=\sin (\alpha).\]
Basic identities
Basic identities
\begin{eqnarray} \sin^2(A)+\cos^2(A)& =& 1.\\
1+\tan^2(A)&=&\sec^2(A).\\
1+\cot^2(A)&=&\csc^2(A).\\
\cos(A+B)&=&\cos(A)\cos(B)-\sin(A) \sin(B).\\
\cos(A-B)&=&\cos(A)\cos(B)+\sin(A) \sin(B).\\
\sin(A+B)&=&\sin(A)\cos(B)+\cos(A) \sin(B).\\
\sin(A-B)&=&\sin(A)\cos(B)-\cos(A) \sin(B).\\
\sin(2A)&=&2 \sin(A) \cos (A).\\
\cos(2A)&=& \cos^2(A)- \sin^2(A)\\
&=& 2 \cos^2(A)-1\\
&=& 1-2 \sin^2(A).\\
\tan(A+B)&= &\displaystyle\frac{\tan (A) + \tan (B)}{1-\tan (A) \tan (B)}.\\
\tan(A-B)&= &\displaystyle\frac{\tan (A) - \tan (B)}{1+\tan (A) \tan (B)}.\\
\tan(2A)&= &\displaystyle\frac{2\tan (A) }{1-\tan^2 (A) }.\\
\end{eqnarray}


