2.2E: Exercises
This page is a draft and is under active development.
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise 2.2E.1
In exercises 1 - 4, consider the graph of the functiony=f(x) shown here. Which of the statements about y=f(x) are true and which are false? Explain why a statement is false.
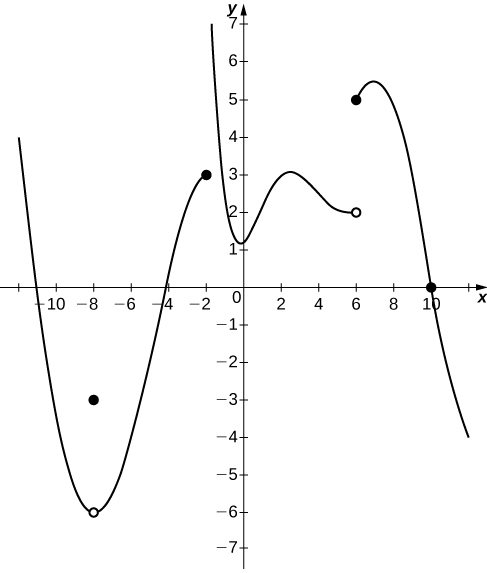
1) limx→10f(x)=0
2) limx→−2+f(x)=3
- Answer
- False; limx→−2+f(x)=+∞
3) limx→−8f(x)=f(−8)
4) limx→6f(x)=5
- Answer
- False; limx→6f(x) DNE since limx→6−f(x)=2 and limx→6+f(x)=5.
Exercise 2.2E.2
In exercises 1 - 5, use the following graph of the function y=f(x) to find the values, if possible. Estimate when necessary.
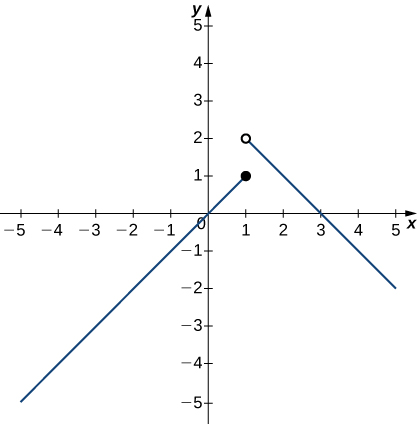
1) limx→1−f(x)
2) limx→1+f(x)
- Answer
- 2
3) limx→1f(x)
4) limx→2f(x)
- Answer
- 1
5) f(1)
Exercise 2.2E.3
In exercises 1 - 4, use the graph of the function y=f(x) shown here to find the values, if possible. Estimate when necessary.
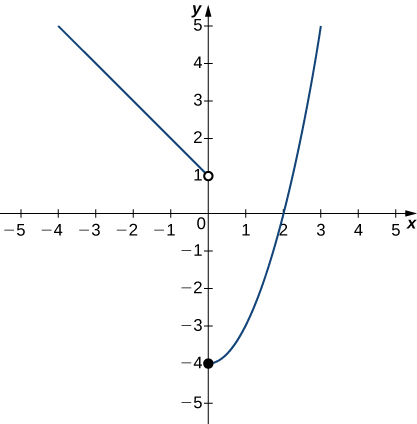
1) limx→0−f(x)
- Answer
- 1
2) limx→0+f(x)
3) limx→0f(x)
- Answer
- DNE
4) limx→2f(x)
Exercise 2.2E.4
In exercises 1 - 6, use the graph of the function y=f(x) shown here to find the values, if possible. Estimate when necessary.
![A graph of a piecewise function with three segments, all linear. The first exists for x < -2, has a slope of 1, and ends at the open circle at (-2, 0). The second exists over the interval [-2, 2], has a slope of -1, goes through the origin, and has closed circles at its endpoints (-2, 2) and (2,-2). The third exists for x>2, has a slope of 1, and begins at the open circle (2,2).](https://math.libretexts.org/@api/deki/files/1897/CNX_Calc_Figure_02_02_204.jpeg?revision=1&size=bestfit&width=417&height=424)
1) limx→−2−f(x)
- Answer
- 0
2) limx→−2+f(x)
3) limx→−2f(x)
- Answer
- DNE
4) limx→2−f(x)
5) limx→2+f(x)
- Answer
- 2
6) limx→2f(x)
Exercise 2.2E.5
1. In exercises a-c, use the graph of the function y=g(x) shown here to find the values, if possible. Estimate when necessary.
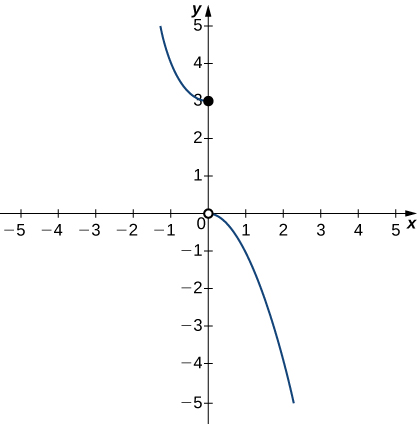
a) limx→0−g(x)
- Answer
- 3
b) limx→0+g(x)
c) limx→0g(x)
- Answer
- DNE
2. In exercises a-c, use the graph of the function y=h(x) shown here to find the values, if possible. Estimate when necessary.
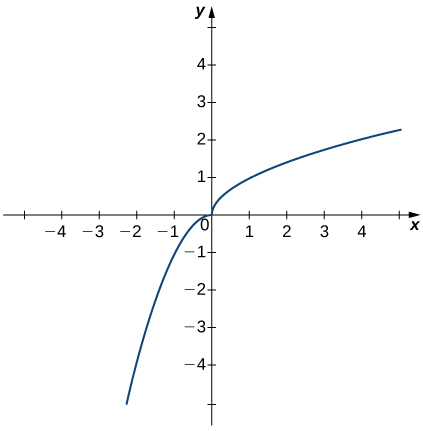
a) limx→0−h(x)
b) limx→0+h(x)
- Answer
- 0
c) limx→0h(x)
Exercise 2.2E.6
In exercises a-e, use the graph of the function y=f(x) shown here to find the values, if possible. Estimate when necessary.
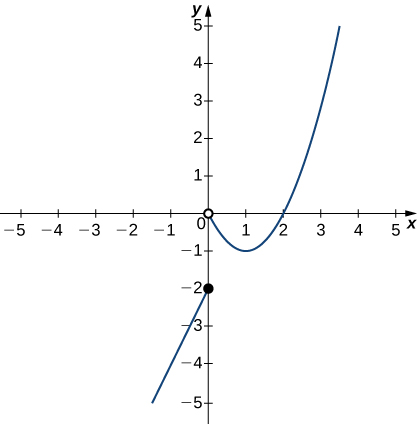
a) limx→0−f(x)
- Answer
- −2
b) limx→0+f(x)
c) limx→0f(x)
- Answer
- DNE
d) limx→1f(x)
e) limx→2f(x)
- Answer
- 0
Exercise 2.2E.7
In exercises 1 - 5, sketch the graph of a function with the given properties.
1) limx→2f(x)=1,limx→4−f(x)=3,limx→4+f(x)=6,x=4 is not defined.
2) limx→−∞f(x)=0,limx→−1−f(x)=−∞,limx→−1+f(x)=∞,limx→0f(x)=f(0),f(0)=1,limx→∞f(x)=−∞
- Answer
-
Answers may vary
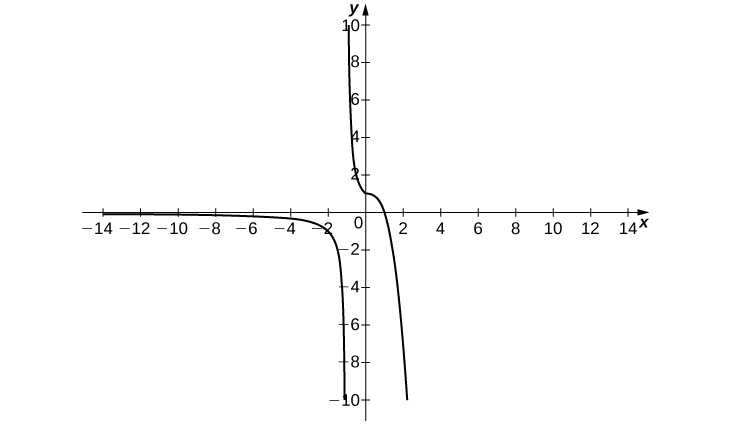
3) limx→−∞f(x)=2,limx→3−f(x)=−∞,limx→3+f(x)=∞,limx→∞f(x)=2,f(0)=−13
4) limx→−∞f(x)=2,limx→−2f(x)=−∞,limx→∞f(x)=2,f(0)=0
- Answer
-
Answer may vary
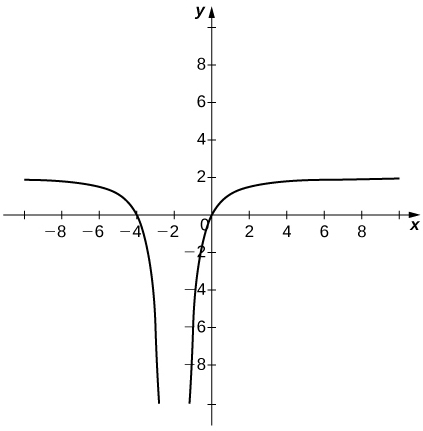
5) limx→−∞f(x)=0,limx→−1−f(x)=∞,limx→−1+f(x)=−∞,f(0)=−1,limx→1−f(x)=−∞,limx→1+f(x)=∞,limx→∞f(x)=0
Exercise 2.2E.8
1) Shock waves arise in many physical applications, ranging from supernovas to detonation waves. A graph of the density of a shock wave with respect to distance, x, is shown here. We are mainly interested in the location of the front of the shock, labeled XSF in the diagram.
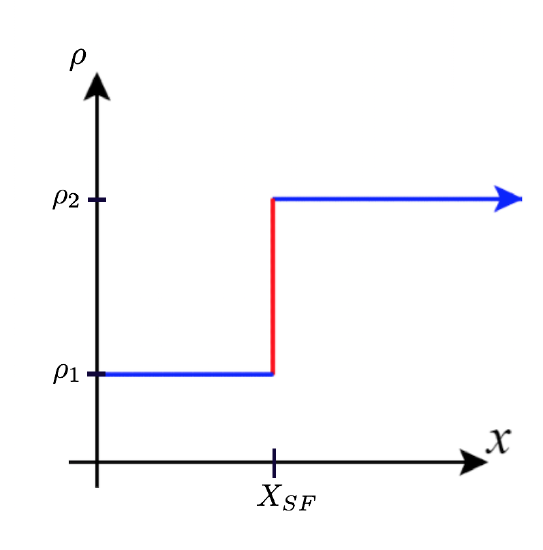
a. Evaluate limx→X+SFρ(x).
b. Evaluate limx→X−SFρ(x).
c. Evaluate limx→XSFρ(x). Explain the physical meanings behind your answers.
- Answer
- a. ρ2 b. ρ1 c. DNE unless ρ1=ρ2. As you approach XSF from the right, you are in the high-density area of the shock. When you approach from the left, you have not experienced the “shock” yet and are at a lower density.
2) A track coach uses a camera with a fast shutter to estimate the position of a runner with respect to time. A table of the values of position of the athlete versus time is given here, where x is the position in meters of the runner and t is time in seconds. What is limt→2x(t)? What does it mean physically?
| t(sec) | x(m) |
|---|---|
| 1.75 | 4.5 |
| 1.95 | 6.1 |
| 1.99 | 6.42 |
| 2.01 | 6.58 |
| 2.05 | 6.9 |
| 2.25 | 8.5 |
Exercise 2.2E.9 Terms and Concepts
- What are the ways in which a limit may fail to exist?
- T/F: If limx→1−f(x)=5, then limx→1f(x)=5
- T/F: If limx→1−f(x)=5, then limx→1+f(x)=5
- T/F: If limx→1f(x)=5, then limx→1−f(x)=5
- T/F: If limx→1−f(x)=−∞, then limx→1+f(x)=∞.
- T/F: If limx→5f(x)=∞, then f has a vertical asymptote at x=5.
- Answer
-
Under construction.
Exercise 2.2E.10: Finding limits using Graphs
Evaluate each expression using the given graph of f(x).
1.
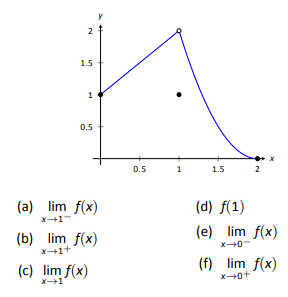
- Answer
-
(a)2,(b)2,(c) 2,(d) 1, (e)DNE, (f)1
2.
- Answer
-
Under construction.
3.
- Answer
-
Under construction.
4.
- Answer
-
Under construction.
- Answer
-
Under construction.
5..
- Answer
-
Under construction.
6.
- Answer
-
Under construction.
7.
- Answer
-
Under construction.
Exercise 2.2E.11: Infinite limits
In Exercises 1-6, evaluate the given limits using the graph of the function.
1. f(x)=1(x+1)2
(a) limx→−1−f(x)
(b) limx→−1+f(x)
2. f(x)=1(x−3)(x−5)2
(a) limx→3−f(x)
(b) limx→3+f(x)
(c) limx→3f(x)
(d) limx→5−f(x)
(e) limx→5+f(x)
(f) limx→5f(x)
3. f(x)=1ex+1
(a) limx→−∞f(x)
(b) limx→∞f(x)
(c) limx→0−f(x)
(d) limx→0+f(x)
4. f(x)=x2sin(πx)
(a) limx→−∞f(x)
(b) limx→∞f(x)
5. f(x)=cos(x)
(a) limx→−∞f(x)
(b) limx→∞f(x)
6. f(x)=2x+10
(a) limx→−∞f(x)
(b) limx→∞f(x)
- Answer
-
Under construction.
Exercise 2.2E.11: One sided limits
Given f(x)={x3+1 if x<00 if x=0√x+1−2 if x>0
Identify each limit:
- limx→0−f(x)
- limx→0+f(x)
- limx→0f(x)
- limx→−1f(x)
- limx→3f(x)
- Hint:
-
Draw a graph.
- Answer
-
11, -1, DNE, 0, 0
- Solution:
-
- limx→0−f(x)=03+11
- limx→0+f(x)=√0+1−2=−1
- Since limx→0−f(x)≠limx→0+f(x), limx→0f(x)= DNE. \
- limx→−1f(x)=(−1)3+1=0
- limx→3f(x)=√3+1−2=0
Exercise 2.2E.12: Infinite limits
limy→6−y+6y2−36
- Answer
-
Since limy→6−y+6y2−36=120, and 5.9+6(5.9)2−36<0,
limy→6−y+6y2−36=−∞.
Contributors and Attributions
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

