2.6E: Excercises
- Page ID
- 10662
This page is a draft and is under active development.
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise \(\PageIndex{1}\)
For exercises 1 - 8, determine the point(s), if any, at which each function is discontinuous. Classify any discontinuity as jump, removable, infinite, or other.
1) \(f(x)=\dfrac{1}{\sqrt{x}}\)
- Answer
- The function is defined for all \(x\) in the interval \((0,∞)\).
2) \(f(x)=\dfrac{2}{x^2+1}\)
3) \(f(x)=\dfrac{x}{x^2−x}\)
- Answer
- Removable discontinuity at \(x=0\); infinite discontinuity at \(x=1\).
4) \(g(t)=t^{−1}+1\)
5) \(f(x)=\dfrac{5}{e^x−2}\)
- Answer
- Infinite discontinuity at \(x=\ln 2\)
6) \(f(x)=\dfrac{|x−2|}{x−2}\)
7) \(H(x)=\tan 2x\)
- Answer
- Infinite discontinuities at \(x=\dfrac{(2k+1)π}{4}\), for \(k=0,\,±1,\,±2,\,±3,\,…\)
8) \(f(t)=\dfrac{t+3}{t^2+5t+6}\)
Exercise \(\PageIndex{2}\)
For exercises 1 - 6, decide if the function continuous at the given point. If it is discontinuous, what type of discontinuity is it?
1) \(\dfrac{2x^2−5x+3}{x−1}\) at \(x=1\)
- Answer
- No. It is a removable discontinuity.
2) \(h(θ)=\dfrac{\sin θ−\cos θ}{\tan θ}\) at \(θ=π\)
3) \(g(u)=\begin{cases}\dfrac{6u^2+u−2}{2u−1}, & \text{if }u≠12\\ \frac{7}{2}, & \text{if }u=12\end{cases}\), at \(u=\frac{1}{2}\)
- Answer
- Yes. It is continuous.
4) \(f(y)=\dfrac{\sin(πy)}{\tan(πy)}\), at \(y=1\)
5) \(f(x)=\begin{cases}x^2−e^x, & \text{if } x<0\\x−1, & \text{if }x≥0\end{cases}\), at \(x=0\)
- Answer
- Yes. It is continuous.
6) \(f(x)=\begin{cases}x\sin(x), & \text{if }x≤π\\ x\tan(x), & \text{if }x>π\end{cases}\), at \(x=π\)
Exercise \(\PageIndex{3}\)
In exercises 1 - 5, find the value(s) of \(k\) that makes each function continuous over the given interval.
1) \(f(x)=\begin{cases}3x+2, & \text{if }x<k\\2x−3, & \text{if }k≤x≤8\end{cases}\)
- Answer
- \(k=−5\)
2) \(f(θ)=\begin{cases}\sin θ, & \text{if }0≤θ<\frac{π}{2}\\ \cos(θ+k), & \text{if }\frac{π}{2}≤θ≤π\end{cases}\)
3) \(f(x)=\begin{cases}\dfrac{x^2+3x+2}{x+2}, & \text{if }x≠−2\\ k, & \text{if }x=−2\end{cases}\)
- Answer
- \(k=−1\)
4) \(f(x)=\begin{cases}e^{kx}, & \text{if }0≤x<4\\x+3, & \text{if }4≤x≤8\end{cases}\)
5) \(f(x)=\begin{cases}\sqrt{kx}, & \text{if }0≤x≤3\\x+1, & \text{if }3<x≤10\end{cases}\)
- Answer
- \(k=\frac{16}{3}\)
Exercise \(\PageIndex{4}\)
In exercises 1 - 3, use the Intermediate Value Theorem (IVT).
1) Show that the equation \(x^3+x^2-2x-1=0\) has at least one solution in the interval \([1,3]\).
- Answer
-
Let \(f(x)= x^3+x^2-2x-1\). Then \(f(x)\) is continuous and \(f(1)=-1\) and \(f(3)=29\).
Since \(-1<0<29\),by the Intermediate Value Theorem there exist at least one real number \(k\) in the interval \([1,3]\) such that \(f(k)=0\).
2) Let \(h(x)=\begin{cases}3x^2−4, & \text{if }x≤2\\5+4x, & \text{if }x>2\end{cases}\) Over the interval \([0,4]\), there is no value of \(x\) such that \(h(x)=10\), although \(h(0)<10\) and \(h(4)>10\). Explain why this does not contradict the IVT.
3) A particle moving along a line for time \(t\) has a position function \(s(t)\), which is continuous. Assume \(s(2)=5\) and \(s(5)=2\). Another particle moves such that its position is given by \(h(t)=s(t)−t\). Explain why there must be a value \(c\) for \(2<c<5\) such that \(h(c)=0\).
- Answer
- Since both \(s\) and \(y=t\) are continuous everywhere, then \(h(t)=s(t)−t\) is continuous everywhere and, in particular, it is continuous over the closed interval [\(2,5\)]. Also, \(h(2)=3>0\) and \(h(5)=−3<0\). Therefore, by the IVT, there is a value \(x=c\) such that \(h(c)=0\).
Exercise \(\PageIndex{5}\)
1) [T] Use the statement “The cosine of \(t\) is equal to \(t\) cubed."
a. Write a mathematical equation of the statement.
b. Prove that the equation in part a. has at least one real solution.
c. Use a calculator to find an interval of length \(0.01\) that contains a solution.
- Answer
-
(b)Let \(f(t)=\cost(t)-t^3. \) Then \(f(t)\) is continuous everywhere. Consider the interval \([0,\dfrac{\pi}{2}]\). Now \(f(t)\) is continous \([0,\pi/2]\),
\(f(0)=\cos(0)-0^3=1>0) and \(f(\dfrac{\pi}{2})=\cos(\dfrac{\pi}{2})-(\dfrac{\pi}{2})^3=-\dfrac{\pi^3}{8} <0.\) Hence by the IVT, \(f(t)\) has at least one \(c \in (0,\dfrac{\pi}{2})\) such that \(f(c)=0.\)
2) Apply the IVT to determine whether \(2^x=x^3\) has a solution in one of the intervals [\(1.25,1.375\)] or [\(1.375,1.5\)]. Briefly explain your response for each interval.
- Answer
- The function \(f(x)=2^x−x^3\) is continuous over the interval [\(1.25,1.375\)] and has opposite signs at the endpoints.
Exercise \(\PageIndex{6}\)
1) Consider the graph of the function \(y=f(x)\) shown in the following graph.
![A diagram illustrating the intermediate value theorem. There is a generic continuous curved function shown over the interval [a,b]. The points fa. and fb. are marked, and dotted lines are drawn from a, b, fa., and fb. to the points (a, fa.) and (b, fb.). A third point, c, is plotted between a and b. Since the function is continuous, there is a value for fc. along the curve, and a line is drawn from c to (c, fc.) and from (c, fc.) to fc., which is labeled as z on the y axis.](https://math.libretexts.org/@api/deki/files/2012/CNX_Calc_Figure_02_04_201.jpeg?revision=1&size=bestfit&width=274&height=270)
a. Find all values for which the function is discontinuous.
b. For each value in part a., state why the formal definition of continuity does not apply.
c. Classify each discontinuity as either jump, removable, or infinite.
2) Let \(f(x)=\begin{cases}3x, & \text{if }x>1\\ x^3, & \text{if }x<1\end{cases}\).
a. Sketch the graph of \(f\).
b. Is it possible to find a value \(k\) such that \(f(1)=k\), which makes \(f(x)\) continuous for all real numbers? Briefly explain.
- Answer
-
a.
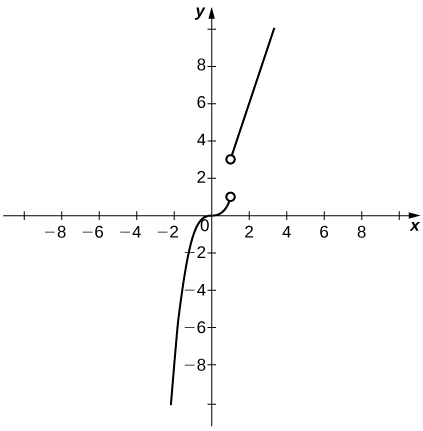
b. It is not possible to redefine \(f(1)\) since the discontinuity is a jump discontinuity.
3) Let \(f(x)=\dfrac{x^4−1}{x^2−1}\) for \(x≠−1,1\).
a. Sketch the graph of \(f\).
b. Is it possible to find values \(k_1\) and \(k_2\) such that \(f(−1)=k\) and \(f(1)=k_2\), and that makes \(f(x)\) continuous for all real numbers? Briefly explain.
- Answer
-
(b) It is possible to redefine both as \(f(-1)=f(1)=2\), since both discontinuities are removable.
4) Sketch the graph of the function \(y=f(x)\) with properties i. through vii.
i. The domain of \(f\) is (\(−∞,+∞\)).
ii. \(f\) has an infinite discontinuity at \(x=−6\).
iii. \(f(−6)=3\)
iv. \(\displaystyle \lim_{x→−3^−}f(x)=\lim_{x→−3^+}f(x)=2\)
v. \(f(−3)=3\)
vi. \(f\) is left continuous but not right continuous at \(x=3\).
vii. \(\displaystyle \lim_{x→−∞}f(x)=−∞\) and \(\displaystyle \lim_{x→+∞}f(x)=+∞\)
- Answer
-
Answers may vary; see the following example:
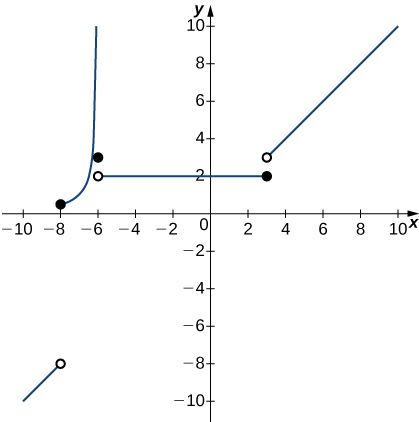
5) Sketch the graph of the function \(y=f(x)\) with properties i. through iv.
i. The domain of \(f\) is [\(0,5\)].
ii. \(\displaystyle \lim_{x→1^+}f(x)\) and \(\displaystyle \lim_{x→1^−}f(x)\) exist and are equal.
iii. \(f(x)\) is left continuous but not continuous at \(x=2\), and right continuous but not continuous at \(x=3\).
iv. \(f(x)\) has a removable discontinuity at \(x=1\), a jump discontinuity at \(x=2\), and the following limits hold: \(\displaystyle \lim_{x→3^−}f(x)=−∞\) and \(\displaystyle \lim_{x→3^+}f(x)=2\).
Exercise \(\PageIndex{7}\)
In following exercises, suppose \(y=f(x)\) is defined for all \(x\). For each description, sketch a graph with the indicated property.
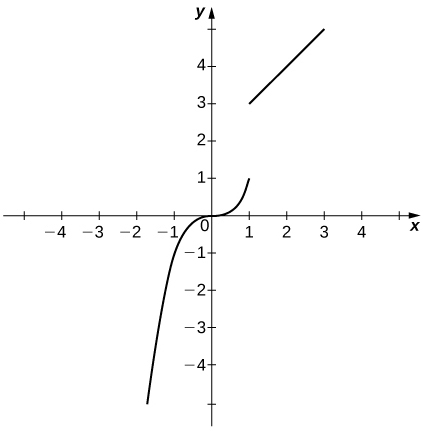
1) Discontinuous at \(x=1\) with \(\displaystyle \lim_{x→−1}f(x)=−1\) and \(\displaystyle \lim_{x→2}f(x)=4\)
- Answer
-
Answers may vary; see the following example:
2) Discontinuous at \(x=2\) but continuous elsewhere with \(\displaystyle \lim_{x→0}f(x)=\frac{1}{2}\)
Exercise \(\PageIndex{8}\)
Determine whether each of the given statements is true. Justify your response with an explanation or counterexample.
1) \(f(t)=\dfrac{2}{e^t−e^{−t}}\) is continuous everywhere.
- Answer
- False. It is continuous over (\(−∞,0\)) ∪ (\(0,∞\)).
2) If the left- and right-hand limits of \(f(x)\) as \(x→a\) exist and are equal, then \(f\) cannot be discontinuous at \(x=a\).
3) If a function is not continuous at a point, then it is not defined at that point.
- Answer
- False. Consider \(f(x)=\begin{cases}x, & \text{if }x≠0\\ 4, & \text{if }x=0\end{cases}\).
4) According to the IVT, \(\cos x−\sin x−x=2\) has a solution over the interval [\(−1,1\)].
5) If \(f(x)\) is continuous such that \(f(a)\) and \(f(b)\) have opposite signs, then \(f(x)=0\) has exactly one solution in [\(a,b\)].
- Answer
- False. Consider \(f(x)=\cos(x)\) on [\(−π,2π\)].
6) The function \(f(x)=\dfrac{x^2−4x+3}{x^2−1}\) is continuous over the interval [\(0,3\)].
7) If \(f(x)\) is continuous everywhere and \(f(a),f(b)>0\), then there is no root of \(f(x)\) in the interval [\(a,b\)].
- Answer
- False. The IVT does not work in reverse! Consider \((x−1)^2\) over the interval [\(−2,2\)].
Exercise \(\PageIndex{9}\)
[T] The following problems consider the scalar form of Coulomb’s law, which describes the electrostatic force between two point charges, such as electrons. It is given by the equation \(F(r)=k_e\dfrac{|q_1q_2|}{r^2}\), where \(k_e\) is Coulomb’s constant, \(q_i\) are the magnitudes of the charges of the two particles, and \(r\) is the distance between the two particles.
1) To simplify the calculation of a model with many interacting particles, after some threshold value \(r=R\), we approximate \(F\) as zero.
a. Explain the physical reasoning behind this assumption.
b. What is the force equation?
c. Evaluate the force \(F\) using both Coulomb’s law and our approximation, assuming two protons with a charge magnitude of \(1.6022×10^{−19}\) coulombs (C), and the Coulomb constant \(k_e=8.988×10^9Nm^2/C^2\) are 1 m apart. Also, assume \(R<1\) m. How much inaccuracy does our approximation generate? Is our approximation reasonable?
d. Is there any finite value of R for which this system remains continuous at R?
2) Instead of making the force \(0\) at \(R\), we let the force be \(10−20\) for \(r≥R\). Assume two protons, which have a magnitude of charge \(1.6022×10^{−19}\;C\), and the Coulomb constant \(k_e=8.988×10^9\;Nm^2/C^2\). Is there a value \(R\) that can make this system continuous? If so, find it.
- Answer
- \(R=0.0001519\) m
Exercise \(\PageIndex{10}\)
The following problems consider a rocket launch from Earth’s surface. The force of gravity on the rocket is given by \(F(d)=−mk/d^2\), where m is the mass of the rocket, \(d\) is the distance of the rocket from the center of Earth, and \(k\) is a constant.
1) [T] Determine the value and units of \(k\) given that the mass of the rocket on Earth is 3 million kg. (Hint: The distance from the center of Earth to its surface is 6378 km.)
2) [T] After a certain distance \(D\) has passed, the gravitational effect of Earth becomes quite negligible, so we can approximate the force function by \(F(d)=\begin{cases}−\dfrac{mk}{d^2}, & \text{if }d<D\\ 10,000, & \text{if }d≥D\end{cases}\). Find the necessary condition \(D\) such that the force function remains continuous.
- Answer
- \(D=63.78\) km
3) As the rocket travels away from Earth’s surface, there is a distance D where the rocket sheds some of its mass, since it no longer needs the excess fuel storage. We can write this function as \(F(d)=\begin{cases} −\dfrac{m_1k}{d^2}, & \text{if }d<D \\ −\dfrac{m_2k}{d^2}, & \text{if }d≥D\end{cases}\). Is there a value of \(D\) such that this function is continuous, assuming \(m_1≠m_2\)?
Exercise \(\PageIndex{11}\)
In the following Exercises, prove each function is continuous everywhere.
1) \(f(θ)=\sin θ\)
- Answer
- For all values of \(a\), \(f(a)\) is defined, \(\displaystyle \lim_{θ→a}f(θ)\) exists, and \(\displaystyle \lim_{θ→a}f(θ)=f(a)\). Therefore, \(f(θ)\) is continuous everywhere.
2) \(g(x)=|x|\)
3) Where is \(f(x)=\begin{cases} 0, & \text{if } x \text{ is irrational}\\ 1, & \text{if }x\text{ is rational}\end{cases}\) continuous?
- Answer
- Nowhere
Exercise \(\PageIndex{12}\): Terms and Cocepts
- In your own words, describe what it means for a function to be continuous.
- In your own words, describe what the Intermediate Value Theorem states.
- What is a “root” of a function?
- T/F: If \(f\) is defined on an open interval containing c, and \(\lim\limits_{x\to c} f(x)\) exists, then \(f\) is continuous at c.
- T/F: If \(f\) is continuous at c, then \(\lim\limits_{x\to c} f(x)\) exist T/F: If \(f\) is continuous at c, then \(\lim\limits_{x\to c^+} f(x)=f(c)\).
- T/F: If \(f\) is continuous on [a, b], then \(\lim\limits_{x\to a^-} f(x)=f(a)\).
- T/F: If f is continuous on [0, 1) and [1, 2), then \(f\) is continuous on [0, 2).
- T/F: The sum of continuous functions is also continuous.
- Answer
-
8. T
Exercise \(\PageIndex{13}\)
Determine on which interval(s) the given function is continuous.
- \(f(x)=x^2-3x+9\)
- \(g(x) = \sqrt{x^2-4}\)
- \(h(k) = \sqrt{1-k}+\sqrt{k+1}\)
- \(f(t) = \sqrt{5t^2-30}\)
- \(g(t) = \frac{1}{\sqrt{1-t^2}}\)
- \(g(x) = \frac{1}{1+x^2}\)
- \(f(x) = e^x\)
- \(g(s) = \ln s \)
- \(h(t) = \cos t\)
- \(f(k) = \sqrt{1-e^k}\)
- \(f(x) = \sin (e^x+x^2)\)
- Answer
-
11. every where.
Exercise \(\PageIndex{14}: Countinuity\)
For what values of \(x\), is \(f\) continuous:
1. Given \[f(x)= \left\{ \begin{array}{ccc}
\displaystyle \frac{x^2-5x+6}{3-x} & \mbox{ if } x <3\\
\\
-1 & \mbox{ if } x =3 \\
\\
x-2 & \mbox{ if } x >3 \\
\end{array}
\right.\]
2. Given \[f(x)= \left\{ \begin{array}{ccc}
\displaystyle \frac{-6}{x} & \mbox{ if } x \leq -1\\
\\
3x^2 & \mbox{ if } x >-1 \\
\end{array}
\right.\]
3. Given \[f(x)= \left\{ \begin{array}{ccc}
\displaystyle \frac{|x-3|-2}{x(x-1)}& \mbox{ if } x \neq 0,x \neq 1\\
\\
1& \mbox{ if } x =1 \\
\\
1& \mbox{ if } x =0 \\
\end{array}
\right.\]
- Answer
-
\(\mathbb{R}\setminus\{3\},\(\mathbb{R}\setminus\{-1\}, \(\mathbb{R}\setminus\{0,1\}\)
Exercise \(\PageIndex{15}: Countinuity\)
For what values of \(k\), each of the following functions is continuous everywhere:
1. \[f(x)= \left\{ \begin{array}{ccc}
(x+k)^2 & \mbox{ if } x\geq 0\\
\\
(2-x)^2 & \mbox{ if } x <0 \\
\end{array}
\right.\]
2. \[f(x)= \left\{ \begin{array}{ccc}
(x+k) & \mbox{ if } x\leq 2\\
\\
\sqrt{kx^2+20} & \mbox{ if } x >2 \\
\end{array}
\right.\]
3. \[ f(x) = \left\{ \begin{array}{l} 2x+k, x < 3\\ \\ \displaystyle \frac{kx^2 + 1}{7}, x \geq 3\end{array}\right .\]
4. \[ f(x) = \left\{ \begin{array}{cc}
x^2+kx+1 & \mbox{if $x \leq 1$,} \\
\\
2x+3 & \mbox{if $x > 1$.} \end{array} \right.
\]
- Answer
-
\(k=\pm 2, k=\pm 4\)
Exercise \(\PageIndex{16}: Countinuity\)
Given \[f(x)= \left\{ \begin{array}{ccc}
\displaystyle \frac{\sin(2x)}{ax}& \mbox{ if } x < 0,\\
\\
x^2-5& \mbox{ if } 0 \leq x <2 \\
\\
bx-4& \mbox{ if } x \geq 2 \\
\end{array}
\right.\]
- For what value of \(a\), \(f\) is continuous at \(x=0\).
- For what value of \(b\), \(f\) is continuous at \(x=2\).
- Answer
-
\(a=-10, b=3/2\)
Exercise \(\PageIndex{17}: Countinuity\)
Find values of \(k\) and \(m,\) if possible, that will make the function \(f\) continuous everywhere.
\[f(x) = \left\{ \begin{array}{ll} x^2+2, x>1\\m(x+1)+k, & - 1< x \leq 1\\ 2x^2 + x + 5, & x \leq -1. \end{array}\right.\]
- Answer
-
\(k=6 , m=-3/2\)
- Solution:
-
when \(x=1\):
\(\lim_{x \to 1^+} f(x)= \lim_{x \to 1} x^2+2=3\) and
\(\lim_{x \to 1^-} f(x)= \lim_{x \to 1} m(x+1)+k=2m+k=f(1)\),
Since \(f\) is continuous at \(x=1\), \(2m+k=3\).
when \(x=-1\):
\(\lim_{x \to -1^+} f(x)= \lim_{x \to -1} m(x+1)+k=k \) and
\(\lim_{x \to -1^-} f(x)= \lim_{x \to -1} 2x^2+x+5=2-1+5=6=f(1)\),
Since \(f\) is continuous at \(x=-1\), \(k=6\).
Therefore, \(2m+6=3\), implies \(m=-3/2\).
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/
Pamini Thangarajah (Mount Royal University, Calgary, Alberta, Canada)

