2.4E: Exercises
- Page ID
- 10649
This page is a draft and is under active development.
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Exercise \(\PageIndex{1}\)
For the following exercises, find \(\frac{dy}{dx}\) for the given functions:
1) \(y=x^2−secx+1\)
2) \(y=3cscx+\frac{5}{x}\)
3) \(y=x^2cotx\)
4) \(y=x−x^3sinx\)
5) \(y=\frac{secx}{x}\)
6) \(y=sinxtanx\)
7) \(y=(x+cosx)(1−sinx)\)
8) \(y=\frac{tanx}{1−secx}\)
9) \(y=\frac{1−cotx}{1+cotx}\)
10) \(y=cosx(1+cscx)\)
- Answers to odd numbered questions
-
1. \(\frac{dy}{dx}=2x−secxtanx\)
3. \(\frac{dy}{dx}=2xcotx−x^2csc^2x\)
5. \(\frac{dy}{dx}=\frac{xsecxtanx−secx}{x^2}\)
7. \(\frac{dy}{dx}=(1−sinx)(1−sinx)−cosx(x+cosx)\)
9. \(\frac{dy}{dx}=\frac{2csc^2x}{(1+cotx)^2}\)
Exercise \(\PageIndex{2}\)
For the following exercises, find the equation of the tangent line to each of the given functions at the indicated values of \(x\).
1) \( f(x)=−sinx,x=0\)
2) \( f(x)=cscx,\,x=\frac{π}{2}\)
3) \( f(x)=1+cosx,\,x=\frac{3π}{2}\)
4) \( f(x)=secx,\,x=\frac{π}{4}\)
5) \(f(x)=x^2−tanx, \,x=0\)
6) \(f(x)=5cot(x), \,x=\frac{π}{4}\)
- Answers to odd numbered questions
-
1. \(y=−x\)
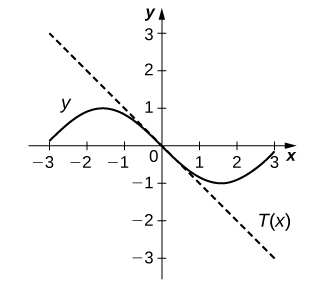
-
3. \(y=x+\frac{2−3π}{2}\)
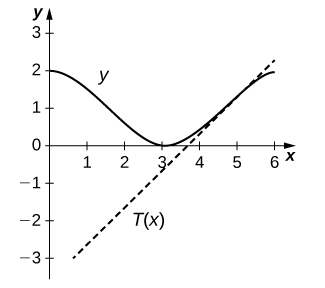
-
5. \(y=x+\frac{2−3π}{2}\)

Exercise \(\PageIndex{3}\)
For the following exercises, find \(\frac{d^2y}{dx^2}\) for the given functions.
1) \(y=xsinx−cosx\)
2) \(y=sinxcosx\)
3) \(y=x−\frac{1}{2}sinx\)
4) \(y=\frac{1}{x}+tanx\)
5) \(y=2cscx\)
6) \(y=sec^2x\)
- Answers to odd numbered questions
-
1. \(3cosx−xsinx\)
3. \(\frac{1}{2}sinx\)
5. \(csc(x)(3csc^2(x)−1+cot^2(x))\)
Exercise \(\PageIndex{4}\)
Find all \(x\) values on the graph of \(f(x)=−3sinxcosx\) where the tangent line is horizontal.
- Answer
-
\(\frac{(2n+1)π}{4}\),where \(n\) is an integer.
Exercise \(\PageIndex{5}\)
Find all \(x\) values on the graph of \(f(x)=x−2cosx\) for \(0<x<2π\) where the tangent line has slope 2.
- Answer
-
Under Construction
Exercise \(\PageIndex{6}\)
Let \(f(x)=cotx.\) Determine the points on the graph of \(f\) for \(0<x<2π\) where the tangent line(s) is (are) parallel to the line \(y=−2x\).
- Answer
-
\((\frac{π}{4},1),(\frac{3π}{4},−1)\)
Exercise \(\PageIndex{7}\)
A mass on a spring bounces up and down in simple harmonic motion, modeled by the function \(s(t)=−6cost\) where s is measured in inches and t is measured in seconds. Find the rate at which the spring is oscillating at \(t=5\) s.
- Answer
-
Under Construction
Exercise \(\PageIndex{8}\)
Let the position of a swinging pendulum in simple harmonic motion be given by \(s(t)=acost+bsint\). Find the constants \(a\) and \(b\) such that when the velocity is 3 cm/s, \(s=0\) and \(t=0\).
- Answer
-
\(a=0,b=3\)
Exercise \(\PageIndex{9}\)
After a diver jumps off a diving board, the edge of the board oscillates with position given by \(s(t)=−5cost\) cm at \(t\)seconds after the jump.
a. Sketch one period of the position function for \(t≥0\).
b. Find the velocity function.
c. Sketch one period of the velocity function for \(t≥0\).
d. Determine the times when the velocity is 0 over one period.
e. Find the acceleration function.
f. Sketch one period of the acceleration function for \(t≥0\).
- Answer
-
Under Construction
Exercise \(\PageIndex{10}\)
The number of hamburgers sold at a fast-food restaurant in Pasadena, California, is given by \(y=10+5sinx\) where \(y\) is the number of hamburgers sold and x represents the number of hours after the restaurant opened at 11 a.m. until 11 p.m., when the store closes. Find \(y'\) and determine the intervals where the number of burgers being sold is increasing.
- Answer
-
\(y′=5cos(x)\), increasing on \((0,\frac{π}{2}),(\frac{3π}{2},\frac{5π}{2})\), and \((\frac{7π}{2},12)\)
Exercise \(\PageIndex{11}\)
The amount of rainfall per month in Phoenix, Arizona, can be approximated by \(y(t)=0.5+0.3cost\), where t is months since January. Find \(y′\)and use a calculator to determine the intervals where the amount of rain falling is decreasing.
- Answer
-
Under Construction
Exercise \(\PageIndex{12}\)
For the following exercises, use the quotient rule to derive the given equations.
1) \(\frac{d}{dx}(cotx)=−csc^2x\)
2) \(\frac{d}{dx}(secx)=secxtanx\)
3) \(\frac{d}{dx}(cscx)=−cscxcotx\)
- Answer
-
Under Construction
Exercise \(\PageIndex{13}\)
For the following exercises, find the requested higher-order derivative for the given functions.
- \(\frac{d^3y}{dx^3}\) of \(y=3cosx\)
- \(\frac{d^2y}{dx^2}\) of \(y=3sinx+x^2cosx\)
- \(\frac{d^4y}{dx^4}\) of \(y=5cosx\)
- \(\frac{d^2y}{dx^2}\) of \(y=secx+cotx\)
- \(\frac{d^3y}{dx^3}\) of \(y=x^{10}−secx\)
- Answers to odd numbered questions
-
1. \(3sinx\)
3. \(5cosx\)
5. \(720x^7−5tan(x)sec^3(x)−tan^3(x)sec(x)\)
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

