3.1: Symmetric Groups
- Page ID
- 131846
Let \(n\in \mathbb{N}\). Let \(X=\{1,\ldots,n\}\), be a set. Then 
\(S_n\) is the set of all the bijections from \(X\) to \(X\) (permutations). Note that there are \(n!\) permutations. The operation \(\star : = \) composition of bijections. Note that it is a right-to-left composition.
\(S_n\) with compositions forms a group; this group is called a Symmetric group. \(S_n\) is a finite group of order \(n!\) and are permutation groups consisting of all possible permutations of n objects. Identity permutation is denoted as \(e\). We will denote a permutation by \(\sigma = \begin{bmatrix} 1 & 2& 3& \cdots & n\\
\sigma(1) & \sigma(2) & \sigma(3) & \cdots & \sigma(n) \end{bmatrix} \in S_n\)
Let \(\sigma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
2 & 4 & 3 & 5 & 1 \end{bmatrix} \in S_5\) and
\( \gamma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 4 & 1 & 2 & 3 \end{bmatrix} \in S_5 \).
Consider \(\gamma \circ \sigma = \gamma \sigma =\) \(\begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 4 & 1 & 2 & 3 \end{bmatrix} \begin{bmatrix} 1 & 2& 3& 4 & 5\\
2 & 4 & 3 & 5 & 1 \end{bmatrix}= \begin{bmatrix} 1 & 2& 3& 4 & 5\\
4 & 2 & 1 & 3 & 5 \end{bmatrix} \)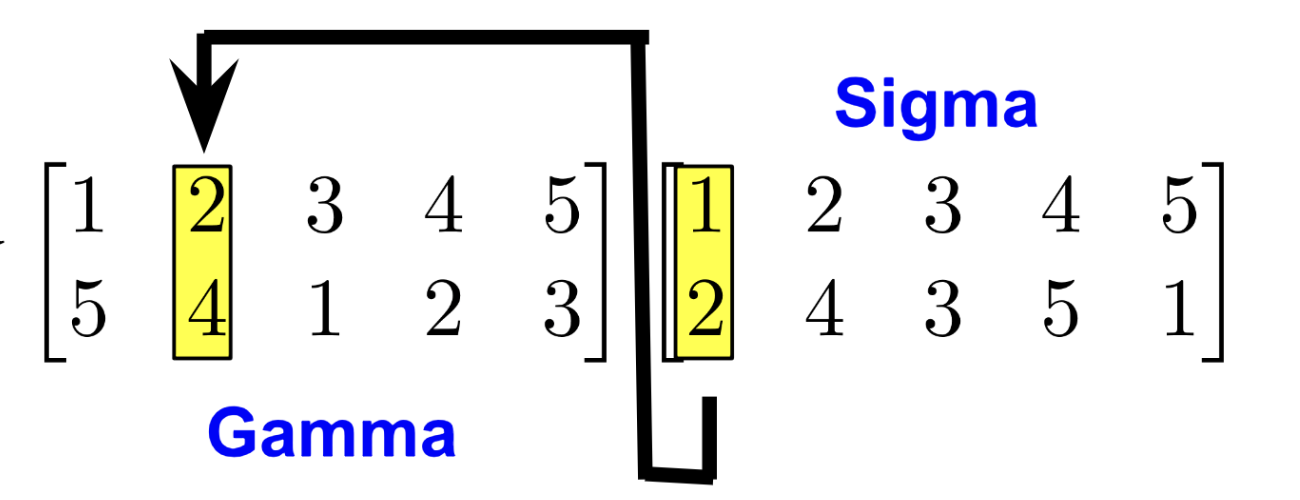
The process of moving from one function to another is illustrated on the right. Note the system is closed since it is a bijection. Completing the process, we obtain the following:
Note, if we switch the order of the functions are switched, we obtain: \(\sigma \gamma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
1 & 5 & 2 & 4 & 3 \end{bmatrix}\).
Note that \(\sigma \gamma \ne \gamma \sigma\). To prove not abelian, we need only show that for any one element, \(k\), \(\sigma \gamma(k) \ne \gamma \sigma(k)\).
The inverse of a permutation \(\sigma\) is the inverse of the function \(\sigma\), and it is denoted by \(\sigma^{-1}\).
Thus, \(\sigma^{-1} \sigma=\sigma \sigma^{-1}=e.\)
Let \(\sigma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
2 & 4 & 3 & 5 & 1 \end{bmatrix} \in S_5\). Then Let \(\sigma^{-1} = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 1 & 3 & 2 & 4 \end{bmatrix} \in S_5\).
Cycle Notation
Cycle notation, a simple and straightforward method, is a convenient way to represent permutations in the symmetric group. For example:
Let \(\gamma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 4 & 1 & 2 & 3 \end{bmatrix}=(1,5,3)(2,4)\).
This can be read as 1 goes to 5, 5 goes to 3, and 3 goes back to 1. Then 2 goes to 4, and then 4 goes back to 2.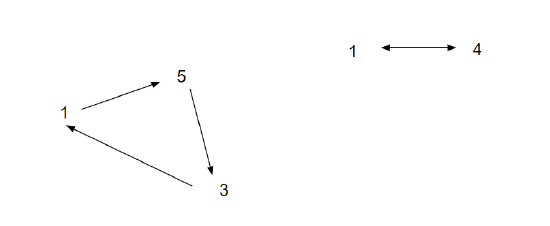
\((1,5,3)\) is called cycle of \(\gamma\) of length \(3\).
- \((1,2,4,5)\) means that 1 goes to 2, 2 goes to 4, 4 goes to 5 and 5 goes to 1. Note that 3 is not included, so 3 goes to 3.
- There is no cycle notation in the case of the identity, \(e\), and we use \(e\).
-
The cycles are always listed in a logical and clear order-descending order of their smallest element.
-
If the permutation fixes an element (i.e., it remains unchanged), it is often omitted from the cycle notation.
Disjoint cycles mean that the elements involved in one cycle are distinct from those in another.
Two cycles in \(S_n\), \(\gamma=(a_1,\ldots,a_k)\) and \(\sigma=(b_1,\ldots,b_l)\) are disjoint if \(a_i \ne b_j, \; \forall i,j\).
Note that the length of the cycles does not need to be the same.
Example: \((1, 2)\) and \((3, 4)\) are disjoint, but \((1, 2, 3)\) and \((3, 4)\) are not disjoint.
Let \( \sigma = \begin{bmatrix} 1 & 2& 3& 4 & 5& 6 & 7 & 8 & 9 &10 &11&12\\
12 & 2 & 3 & 1 & 11 & 9 & 5 &10 & 6 &4& 7 & 8 \end{bmatrix} \)
Then a cycle decomposition of
\( \sigma = (1, 12, 8, 10, 4) (2)(3)(5,11,7)(6,9)= (1, 12, 8, 10, 4) (5,11,7)(6,9) \).
Note that these are disjoint cycles; therefore, they commute.
1. Disjoint cycles are commutative.
Let \(\gamma\) and \(\sigma\) be disjoint cycles, then \(\gamma \sigma = \sigma \gamma\).
2. Every permutation of a finite set can be written as a cycle or a product of disjoint cycles.
The inverse of a cycle:
\((a_1, a_2, \cdots, a_k)^{-1}= (a_k, a_{k-1}, \cdots, a_1)\)
\( (1,2,3)^{-1} = (3,2,1) \), and \((1,2)^{-1}=(2,1)=(1,2).\)
Let \( \sigma = \begin{bmatrix} 1 & 2& 3& 4 & 5& 6 & 7 & 8 & 9 &10 &11&12\\
12 & 2 & 3 & 1 & 11 & 9 & 5 &10 & 6 &4& 7 & 8 \end{bmatrix} = (1, 12, 8, 10, 4) (5,11,7)(6,9). \)
In a cycle decomposition, to find the inverse, just reverse the order of the cycles and find the inverse of each cycle. Hence,
\( \sigma^{-1} =(6,9)^{-1}(5, 11, 7)^{-1} (1, 12, 8, 10, 4)^{-1}=(9,6)(7, 11, 5) (4, 10, 8, 12, 1) \)
\((2,3)(1,2) = (1,3,2) \) Note: one goes to 2 first, then to 2 and then gets to 3.
\((1,2)(2,3)= (1,2,3)=(2,3,1)=(3,2,1)\) Note: Since there is no 1 in the inner function, it goes to itself
then goes to 2, which goes to 3
Type of a permutation
The type of a permutation is the integer partition formed from the cycle lengths in decreasing order. We will denote it by type().
Let \(\gamma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 4 & 1 & 2 & 3 \end{bmatrix}=(1,5,3)(2,4)\).
The type \( (\gamma)=(3,2)\)
Let \(\gamma = \begin{bmatrix} 1 & 2& 3& 4 & 5\\
5 & 4 & 1 & 2 & 3 \end{bmatrix}=(1,5,3)(2,4)\).
The type \( (\gamma)=(3,2)\)
A partition of a positive integer \(n\) is a sum of nonnegative integers \(n=k_1+\cdots+k_s, k_i \in \mathbb{N},\) where the order of the summand is not important. For example: The partitions of \(6\) are \(6, 5+1, 4+2, 4+1+1 , 3+3, 3+2+1, 3+1+1+1, 2+2+2, 2+2+1+1, 2+1+1+1+1, 1+1+1+1+1+1.\)
How many permutations in \(S_6\) have type \((3,2,1)\)?
Type \((3,2,1)\) permutation is of the form \( (_,_,_)(_,_)(_) \). There are \(6!\) ways of filling the blanks. note that each cycle can be restarted anywhere.
Hence, the number of permutations in \(S_6\) have type \((3,2,1)\) is \(\dfrac{6!}{(3)(2)(1)}.\)
How many permutations in \(S_6\) have \(3\) cycles of length \(2\)?
The permutation is of the form \( (_,_)(_,_)(_,_) \). There are \(6!\) ways of filling the blanks. Since each cycle has 2 representations matching this format(by restarting at any 2 places), so divided by \(2^3\).
The order of the whole cycle can be changed while keeping the pattern. Divide by \(3!\) ways to reorder the cycles.
Hence, the number of permutations in \(S_6\) have \(3\) cycles of length \(2\) is \(\dfrac{6!}{(2^3)(3!)}.\)
Suppose the number of cycles of length \(i\) is \(m_i\), for \(i=1, \cdots, k.\) and \(n=m_1+2m_2+\cdots+ km_k.\)
The number of permutations in \(S_n\) of the type \( (m_k, m_k\cdots, m_1) \)is
\(\dfrac{n!}{1^{m_1}2^{m_2}\cdots k^{m_k} {m_1}! m_2! \cdots m_k!}.\)
\(|S_3|=3!=2\cdot 3=6\).
|
Cycle type 111 |
Cycle type 21 |
Cycle type 3 |
|
\(\dfrac{3!}{1^3 3!}=1\) |
\(\dfrac{3!}{1^1 2^1 1!1!}=3\) |
\(\dfrac{3!}{ 3^1 1!1!}=2\) |
Hence, \(S_3= \{e,(1,2),(1,3), (2,3), (1,2,3),(1,3,2)\}\).
|
Cayley Table for \(S_3\) |
||||||
|
e |
(1,2,3) |
(1,3) |
(1,2) |
(2,3) |
(1,3,2) |
|
|
e |
e |
(1,2,3) |
(1,3) |
(1,2) |
(2,3) |
(1,3,2) |
|
(1,2,3) |
(1,2,3) |
(1,3,2) |
(2,3) |
(1,3) |
(1,2) |
e |
|
(1,3) |
(1,3) |
(1,2) |
e |
(1,2,3) |
(1,3,2) |
(2,3) |
|
(1,2) |
(1,2) |
(2,3) |
(1,3,2) |
e |
(1,2,3) |
(1,3) |
|
(2,3) |
(2,3) |
(1,3) |
(1,2,3) |
(1,3,2) |
e |
(1,2) |
|
(1,3,2) |
(1,3,2) |
e |
(1,2) |
(2,3) |
(1,3) |
(1,2,3) |
let’s explore \(S_4\). Note \(S_4\) has \(S_4\) has \(4!=24\) elements.
|
Cycle type 1111 |
Cycle type 211 |
Cycle type 22 |
Cycle type 31 |
Cycle type 4 |
|
\(\dfrac{4!}{1^4 4!}=1\) |
\(\dfrac{4!}{1^2 2^1 2!1!}=6\) |
\(\dfrac{4!}{ 2^2 2!}=3\) |
\(\dfrac{4!}{1^1 3^1 1!1!}=8\) |
\(\dfrac{4!}{4^1 1!}=6\) |
Hence, \[S_4=\{e, (1,2), (1,3), (1,4), (2,3), (2,4), (3,4),(1,2)(3,4), (1,3)(2,4), (1,4)(2,3), (1,2,3), (1,3,2), (2,3,4), (2,4,3), (3,4,1), (3,1,4), (4,1,2), (4,2,1),(1,2,3,4), (1,2,4,3), (1,3,4,2), (1,3,2,4), (1,4,2,3), (1,4,3,2) \}. \]
The following theorem proves that \(S_n\) are non-Abelian for integer n ≥ 3, which means that the order in which we compose permutations matters.
\(S_n\) is non-Abelian for all integers n ≥ 3.
- Proof
-
Let \(a,b \in S_3\).
We will show that \(\thereexist a, b \in S_n, s.t. ab \ne ba \), \(n \ge 3\).
Note \(S_3=\{e,(1,2),(1,3),(2,3),(1,2,3),(1,3,2)\}\).
Let \(a=(1,2)\) and \(b=(2,3)\) both elements of \(S_3\).
Consider \(ab=(1,2)(1,3)=(1,3,2)\) and \(ba=(1,3)(1,2)=(1,2,3)\).
Since \((1,3,2) \ne (1,2,3)\), \(ab\ne ba \; \forall a,b \in S_3\), thus \(S_3\) is non-abelian.
Since \(S_3 \le S_n, \; \forall n \ge 3\), \(S_n\) in non-abelian for \(n\ge 3\).◻
Given \(\alpha, \beta \in S_4\) with \(\alpha \beta =(1,4,3,2), \; \beta \alpha = (1,2,4,3)\), and \(\alpha(1)=4\), deter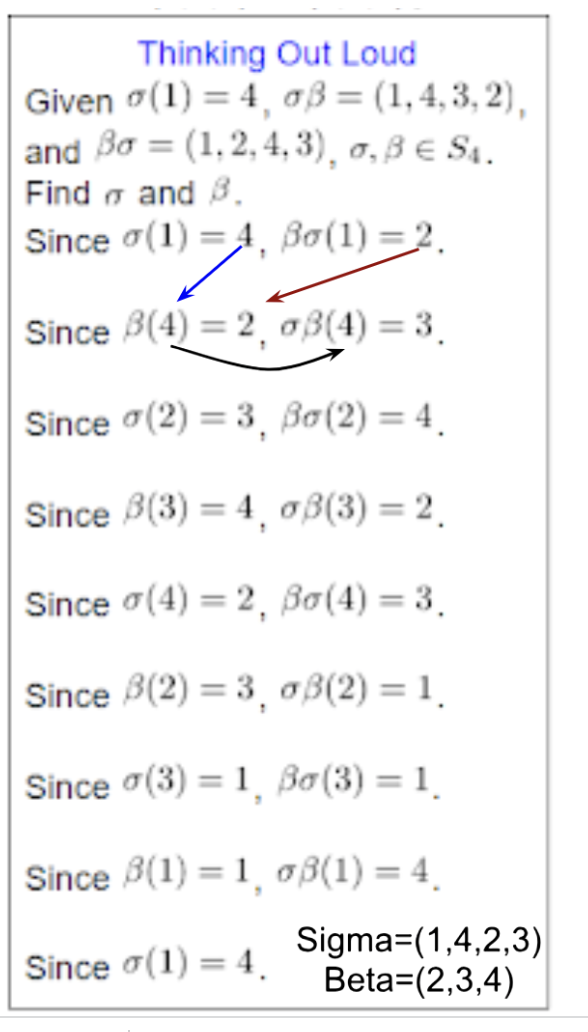
mine \(\alpha\) and \(\beta\).
Solution:
Let \(\alpha=(1,4,c,d)\) and \(\beta=(w,x,y,z)\).
Since \(\alpha(1)=4\) and \(\beta \alpha(1)=2\), implies \(\beta(4)=2\).
Since \(\beta(4)=2\) and \(\alpha \beta(4)=3\), implies \(\alpha(2)=3\).
Since \(\alpha(2)=3\) and \(\beta \alpha(2)=4\), implies \(\beta(3)=4\).
Since \(\beta(3)=4\) and \(\alpha \beta(3)=2\), implies \(\alpha(4)=2\).
Since \(\alpha(4)=2\) and \(\beta \alpha(4)=3\), implies \(\beta(2)=3\).
Since \(\beta(2)=3\) and \(\alpha \beta(2)=1\), implies \(\alpha(3)=1\).
Since \(\alpha(3)=1\) and \(\beta \alpha(3)=1\), implies \(\beta(1)=1\).
\(\alpha=(1,4,2,3)\) and \(\beta=(2,3,4)\).
Then \(\beta \alpha =(2,3,4)(1,4,2,3)=(2,4,3,1)=(1,2,4,3)\).
And \(\alpha \beta =(1,4,2,3)(2,3,4)=(4,3,2,1)=(1,4,3,2)\).
Note that every permutation of a finite set can be written as a cycle or a product of disjoint cycles.
2 Cycle (Transposition)
\((i,j), \; i\le j, \; j\le n, \; i \ne j\).
\((i,j)^{-1}=(j,i)=(i,j)\).
(1, 3, 2) = (1, 2) (1, 3) 1 goes to 3, 3 goes to itself, then to 1 then to 2.
(1, 2, 3) = (1, 3) (1, 2).
(2, 4, 1, 3, 5) = (2, 5) (2, 3) (2, 1) (2, 4)
Note: Any cycle can be written as a composition of two cycles.
A \(k-\)cycle \( (i_1,i_2\cdots, i_k) \) can be decomposed into a product of transpositions. That is,
\( (i_1,i_2\cdots, i_k)=(i_1,i_k)(i_1, i_{k-1})\cdots (i_1,i_2). \)
Every permutation in \(S_n\) can be expressed as a product of 2-cycles (Transpositions). The number of transpositions will either always be even or odd.
If a permutation α can be expressed as a product of an even number of 2-cycles, then every decomposition of α into a product of 2-cycles has an even number of 2-cycles. A similar statement holds for odd.
Permutation parity
Let \(\sigma \in S_n\). (i.e. a permutation)
Then
(1) \(\sigma\) is an even permutation if \(\sigma\) can be expressed as a product of an even number of two cycles.,
(2) \(\sigma\) is an odd permutation if \(\sigma\) can be expressed as a product of an odd number of 2 cycles.
1. let’s explore \(S_4\). Note \(S_4\) has \(S_4\) has \(4!=24\) elements.
Consider \(S_4=\{e, (1,2), (1,3), (1,4), (2,3), (2,4), (3,4),(1,2)(3,4), (1,3)(2,4), (1,4)(2,3), (1,2,3),
(1,3,2), (2,3,4), (2,4,3), (3,4,1), (3,1,4), (4,1,2), (4,2,1),(1,2,3,4), (1,2,4,3), (1,3,4,2), (1,3,2,4), (1,4,2,3), (1,4,3,2) \}\)
2. Find the centre of \(S_4\).
Since all symmetrical groups, \(S_n\), \(n \ge 3\), are non-abelian, the centre of \(S_4\) is trivial, being the identity e, or (1)(2)(3)(4). (what do you think of this proof? Is this a valid argument?)
Alternatively, proof by exhaustion: Having tried all \(x \in S_4\), the only \( x \in S_4\) that satisfies \(xg=gx, \; \forall g \in S_4\) is the identity.
3. Find the cyclic subgroup of \(S_4\) that has an order of 4.
The subgroup of \(S_4, C4 =\{e, (1,2,3,4),(1,3)(2,4),(1,4,3,2) \}\), has an order 4 and is generated by \((1,2,3,4)\).
\((1,2,3,4)^2=(1,3)(2,4)\), \((1,2,3,4)^3=(1,4,3,2)\), and \((1,2,3,4)^4=e\).
4. Find a non-cyclic subgroup of \(S_4\) that has order 4.
The 2-2 cycles together will form an order 4 group.
\(\{e, (1,2)(3,4),(1,3)(2,4),(1,4)(2,3)\}\) is a subgroup of \(S_4\) and has order 4. Note the inverse of \((1,2)(3,4)\) is \((4,3)(2,1)\), which is \((1,2)(3,4)\). Since a similar argument can be made for the other 2-2 cycles, the inverses of each element exist. In addition, the set is closed under composition.
Order of a permutation
Let \(\sigma=(1, 2, 3)\).
Then \(\sigma^2=(1, 2, 3)(1, 2, 3)=(1, 3, 2)=\sigma^{-1}\).
Further \(\sigma ^3=(1, 2, 3)(1, 3, 2)=(1)(2)(3)=e\). We shall refer to \(e\) as 1.
Thus the order of \(\sigma\), \(|\sigma |=3\).
If \(\sigma=(a_1, \ldots, a_k)\), then the \(|\sigma |=k\). (Proof?)
Let \(\gamma = (1, 2, 4)\). Then
\(\gamma^2=(1, 2, 4)(1,2, 4)=(1, 4, 2)\).
\(\gamma^3=(1, 2, 4)(1, 4, 2)=(1)(2)(4)\).
The order of a permutation of a finite set, written in disjoint cycle form, is the least common multiple of the lengths of the cycles.
Find the orders of the 5040 elements of \(S_7.\)
Solution
The longest cycle in \(S_7\) is the one that includes all the elements -- 7. We will show cycle lengths as \(\underline{7}\). Note the underlining. The possible cycles are shown in the table below. Note that the leading term is the longest cycle in the permutation.
|
Cycle type |
Order |
Cycle type |
Order |
Cycle type |
Order |
|
7 |
7 |
4 2 1 |
4 |
3 1 1 1 1 |
3 |
|
6 1 |
6 |
4 1 1 1 |
4 |
2 2 2 1 |
2 |
|
5 2 |
10 |
3 3 1 |
3 |
2 2 1 1 1 |
2 |
|
5 1 1 |
5 |
3 2 2 |
6 |
2 1 1 1 1 1 |
2 |
|
4 3 |
12 |
3 2 1 1 |
6 |
1 1 1 1 1 1 1 |
1 |
Conjugacy classes of \(S_n\)
Recall:
Two elements \(x,y \) in a group \(G\) are conjugate if \(y=gxg^{-1}\) for some \(g\in G\).
Conjugacy classes of \(G\) are subsets of \(G\) in which elements are conjugate to each other.
Two permutations in \(S_n\) are conjugate if and only if they have the same cycle structure, i.e. they have the same cycle type.
Conjugacy classes of \(S_3.\)
Solution
There are three conjugacy classes. Those are \( \{(1,2),(2,3),(1,3)\},\{e\},\{(1,2,3),(3,2,1)\}.\)