4.2: Euclidean algorithm and Bezout's algorithm

Definition: Euclidean Algorithm

The Euclidean Algorithm is an efficient way of computing the GCD of two integers. It was discovered by the Greek mathematician Euclid, who determined that if n goes into x and y, it must go into x-y. Therefore, we can subtract the smaller integer from the larger integer until the remainder is less than the smaller integer. We continue using this process until the remainder is 0, thus leaving us with our GCD.

If \(a,b \in \mathbb{Z} \setminus \{0\}\), then by using division algorithm iteratively, we obtain

\begin{eqnarray*}a &=bq_0+r_0 \\ b &=r_0 q_1+r_1 \\  r_0 &=r_1q_2+r_2\\ \vdots \\ r_{n-2} &=r_{n-1}q_{n}+r_n \\ r_{n}&=r_nq_{n+1}+0 \\ \end{eqnarray*}

Notice that, the last non-zero remainder is \(r_{n}\), such an \(r_n\) exists, since \(|b|>|r_0|>|r_1| \cdots >|r_n|.\) The \(r_n=\gcd(a,b)\).

Example \(\PageIndex{1}\):

Find the GCD of 30 and 650 using the Euclidean Algorithm.
650 / 30 = 21 R 20. Now take the remainder and divide that into the original divisor.
30 / 20 = 1 R 10. Now take the remainder and divide that into the previous divisor.
20 / 10 = 2 R 0. Since we have a remainder of 0, we know that the divisor is our GCD.
Therefore, the GCD of 30 and 650 is 10.

Example \(\PageIndex{2}\):

Find \(\gcd(2420, 230)\).

Note: Work from right to left to follow the steps shown in the image below.

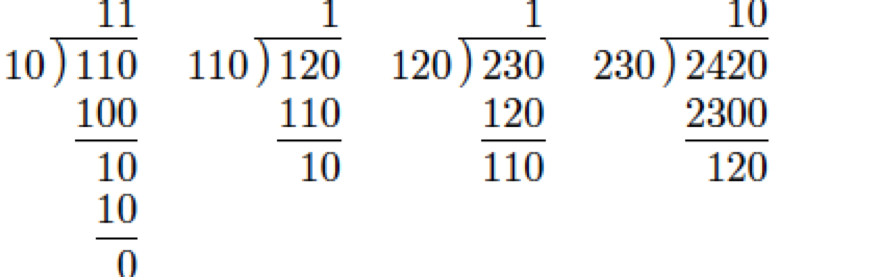
Hence, \(\gcd(2420,230) =10\).

Example \(\PageIndex{3}\):

Find \(\gcd(3915, 825)\).
Note: Work from right to left to follow the steps shown in the image below.

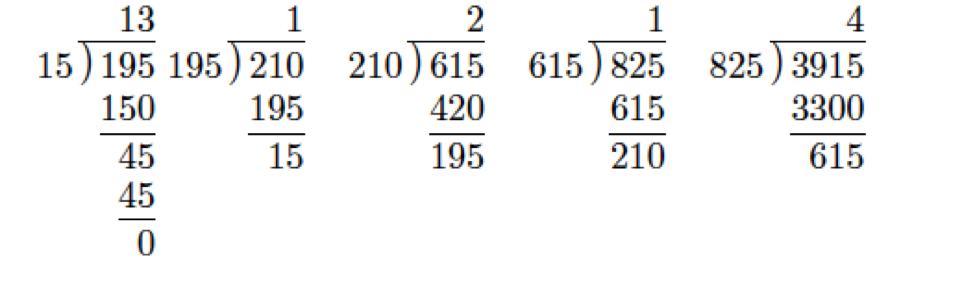
Hence, \(\gcd(3915, 825 )=15\).

Example \(\PageIndex{4}\): Geometric GCD

We want to tile an a ft by b ft (a, b \(\in \mathbb{Z}\)) floor with identical square tiles. What is the largest square tile we can use? \(\gcd(a, b)\).

Consider the following example where \(a=100\) and \(b=44\).

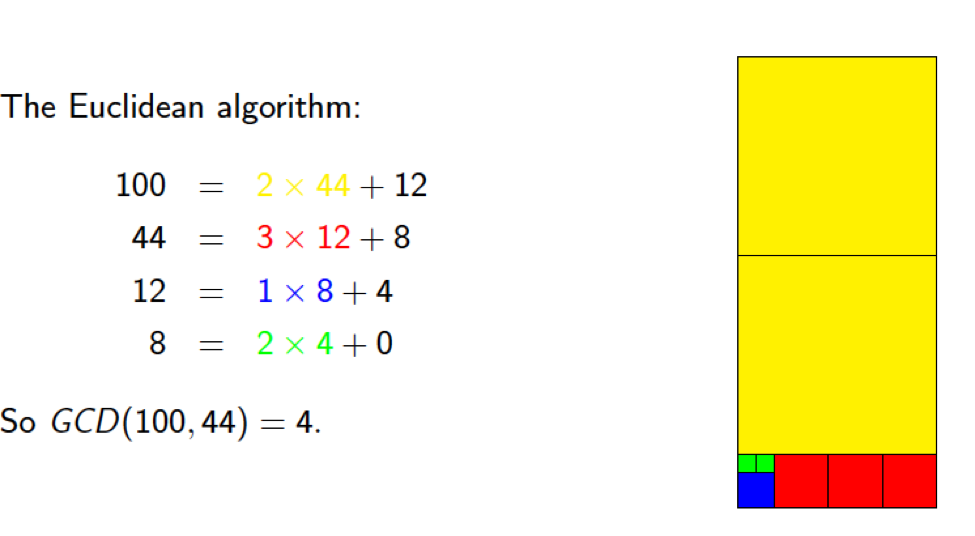
The largest square tile we can use to completely tile a 100 ft by 44 ft floor is a \(4\) ft by \(4\) ft tile.

BEZOUT'S IDENTITY

For integers a and b, let d be the greatest common divisor, d = GCD (a, b). Then there exists integers x and y such that ax+by=d. Any integer that is of the form ax+by, is a multiple of d.

Note

This condition will be a necessary and sufficient condition in the case of \(d=1\). We will prof this result in section 4.4, Relatively Prime numbers.

Bezout Algorithm

Use the Euclidean Algorithm to determine the GCD, then work backwards using substitution. WHEN DOING SUBSTITUTION BE VERY CAREFUL OF THE POSITIVES AND NEGATIVES.

Example \(\PageIndex{5}\)

Find the Bezout Identity for a=34 and b=19.

Solution

First, find the gcd(34, 19).
34 = 19(1) + 15.
19 = 15(1) + 4.
15 = 4(3) + 3.
4 = 3(1) + 1.
3 = 1(3) + 0.
Thus, the gcd(34, 19) = 1.

Next, work backwards to find x and y.
1 = 4 - 1(3).
= 4 - 1(15 - 4(3)) = 4(4) - 1(15).
= 4(19 - 15(1)) -1(15) = 4(19) - 5(15).
= 4(19) - 5(34 - 19(1)) = 9(19) - 5(34).

Thus Bezout's Identity for a=34 and b=19 is 1 = 34(-5) + 19(9).

Example \(\PageIndex{6}\): Tabular Method, yielding GCD and Bezout's Coefficients

 

Find Bezout's Identity for a = 237 and b = 13.

Solution:

(1) Set up the initial table. This step is always the same regardless of which numbers you are trying to find the GCD of.	Iteration	Remainder	Quotient	Coefficients of Bezout’s
	i	r	q	s	t
	0			1	0
	1			0	1
	2

 

(2) Insert numerator into R0C1 (3) Insert denominator into R1C1 (4) Integer divide R0C1 by R1C1 and place result into R1C2 (5) Place remainder from (4) into R2C1   Table at right shows completed steps 1 - 5 of GCD(237,13). Note: 237/13 = 18 R 3	i	r	q	s	t
	0	237		1	0
	1	13	18	0	1
	2	3

 

(6) add new line to table, increment i. (7) RiC2 is integer division Ri-1C1/RiC1 (8) Place remainder from (7) into Ri+1C1 Note: 13/3 = 4 R 1 (9) RiC3 is Ri-2C3 - (Ri-1C2 * R i-1C3) (10) RiC4 is Ri-2C4 - (Ri-1C2 * R i-1C4)	i	r	q	s	t
	0	237		1	0
	1	13	18	0	1
	2	3	4	1	-18
	3	1

 

Repeat steps 6 - 10 until RiC1 = 0 Completed table for GCD(237,13) at right.   GCD (237,13) = 1 = first non zero remainder. Write answer as: GCD(237,13) = 1 = -4(237) + 73(13)   Where -4=s and 73=t. The GCD = 1 indicates that the numbers are relatively prime.	Iteration	Remainder	Quotient	Coefficients of Bezout’s
	i	r	q	s	t
	0	237		1	0
	1	13	18	0	1
	2	3	4	1	-18
	3	1	3	-4	73
	4	0

Thus, the Bezout's Identity for a=237 and b=13 is 1 = -4(237) + 73(13).

Example \(\PageIndex{7}\):

Find the GCD of 149553 and 177741:

First, use the Euclidean Algorithm to determine the GCD.
177741/149553 = 1 R 28188
149553/28188 = 5 R 8613
28188/8613 = 3 R 2349
8613/2349 = 3 R 1566
2349/1566 = 1 R 783
1566/783 = 2 R 0
Because we have a remainder of 0 we have now determined that 783 is the GCD.

Next, find \(x, y \in \mathbb{Z}\) such that 783=149553(x)+177741(y).
Using the answers from the division in Euclidean Algorithm, work backwards.
783= 2349+1566(-1).
1566=8613+2349(-3).
2349=28188+8613(-3).
8613=149553+28188(-5).
28188=177741+149553(-1).
Now substitute in,
783 =2349+1566(-1).
=2349 +(8613 + 2349(-3))(-1)
=2349 +(8613(-1)+2349(3)
=2349(4)+8613(-1)
=(28188+8613(-3))(4)+8613(-1)
=28188(4)+8613(-13)
=28188(4)+(149553+28188(-5))(-13)
=28188(69)+149553(-13)
=(177741+149553(-1))(69)+149553(-13)
=177741(69)+149553(-82)
Thus, Bezout's Identity is 783=177741(69)+149553(-82).

Example \(\PageIndex{8}\):

Let \(a,b \in \mathbb{Z}\). If \(ax+by=12\) for some integers \(x\) and \(y\). Then what are the possible values for \(\gcd(a, b)\). For these values find possible values for \(a, b, x\) and \(y\).

Answer

a	b	x	y	d=gcd(a,b)

Theorem \(\PageIndex{1}\)