6.1: Prime numbers
( \newcommand{\kernel}{\mathrm{null}\,}\)
Definition:
Prime Numbers - integers greater than 1 with exactly 2 positive divisors: 1 and itself.
Let n be a positive integer greater than 1. Then n is called a prime number if n has exactly two positive divisors, 1 and n.
Composite Numbers - integers greater than 1 which are not prime.
Note that: 1 is neither prime nor composite.
There are infinitely many primes, which was proved by Euclid in 100BC.
Example 6.1.1: Method of Sieve of Eratosthenes
Examples of prime numbers are 2 (this is the only even prime number), 3,5,7,9,11,13,17,….
Method of Sieve of Eratosthenes:
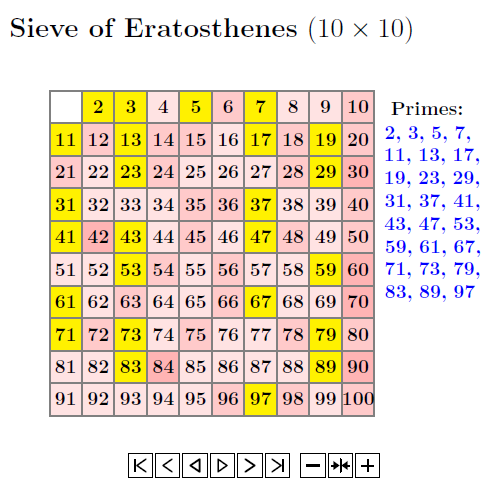
The following will provide us a way to decide given number is prime.
Theorem 6.1.1
Let n be a composite number with exactly 3 positive divisors. Then there exists a prime p such that n=p2.
- Proof
-
Let n be a positive integer with exactly 3 positive divisors. Then two of the positive divisors are 1 and n.
Let d be the third positive divisor. Then 1<d<n and the only positive divisors of d are 1 and d.
Therefore d is prime.
Since d∣n, n=md,m∈Z+.
Since m∣n and 1<m<n,m=d,n=d2.
Thus, d is prime. ◻
Theorem 6.1.2
Every composite number n has a prime divisor less than or equal to √n. If p is a prime number and p∣n, then 1<p≤√n.
- Proof
-
Suppose p be the smallest prime divisor of n. Then there exists an integer m such that n=pm. Assume that p>√n. Then m<√n.
Let q be any prime divisor of m. Then q is also a prime divisor of n and q<m<√n<p. This is a contradiction.
Example 6.1.2:
Is 223 a prime number?
Solution:
The prime numbers <√223 are as follows: 2,3,5,7,11, and 13. Note that 172>223.
Since 223 is not divisible by any of the prime numbers identified above, 223 is a prime number.
Exercise 6.1.3
Is 2011 a prime number?.
- Answer
-
yes.
Theorem 6.1.3: Prime divisibility theorem
Let p be a prime number. If p∣ab,a,b∈Z, then p∣a or p∣b.
- Proof
-
Let p be a prime number and let a,b∈Z. Assume that p∣ab. If p∣a, we are done. So we suppose that p does not divide a. Thus gcd(a,p)=1. Thus there exists x,y∈Z such that 1=ax+py. Hence b=abx+pby. Since p∣ab, ab=pm,m∈Z. Thus b=pmx+pby=p(mx+by). Hence, p∣b.
Theorem 6.1.5
There are infinitely many primes.
- Proof
-
Proof by contradiction.
Suppose there are finitely many primes p1,p2,...,pn, where n is a positive integer. Consider the integer Q such that
Q=p1p2...pn+1.
Notice that Q is not prime. Hence Q has at least a prime divisor, say q. If we prove that q is not one of the primes listed then we obtain a contradiction. Suppose now that q=pi for 1≤i≤n. Thus q divides p1p2...pn and as a result q divides Q−p1p2...pn. Therefore q divides 1. But this is impossible since there is no prime that divides 1 and as a result q is not one of the primes listed.
The following theorem explains the gaps between prime numbers:
Theorem 6.1.5
Let n be an integer. Then there exists n consecutive composite integers.
- Proof
-
Let n be an integer. Consider the sequence of integers (n+1)!+2,(n+1)!+3,...,(n+1)!+n,(n+1)!+(n+1)
Notice that every integer in the above sequence is composite because k divides (n+1)!+k if 2≤k≤(n+1).
Example 6.1.4:
Does there exist a block of 1000000 consecutive integers without a prime number among them?
Solution
Use 1000001! and consider 1000001!+2,…,1000001!+1000001
Example 6.1.5:
Consider the formula y=x2+x+13. Then
1. Find the values y for x=1,⋯,12. How many of these values are prime?
2. Can we conclude that this formula always generates a prime number?
Definition: Twin primes
Two prime numbers are called twin primes if they differ by 2.
Theorem 6.1.6 Fundamental Theorem of Arithmetic (FTA)
Let n∈Z+, then n can be expressed as a product of primes in a unique way. This means
n=pn11pn22⋯pnkk, where p1<p2<...<pk are primes.
Neither the fundamental theorem nor the proof shows us how to find the prime factors. We can use tests for divisibility to find prime factors whenever possible.
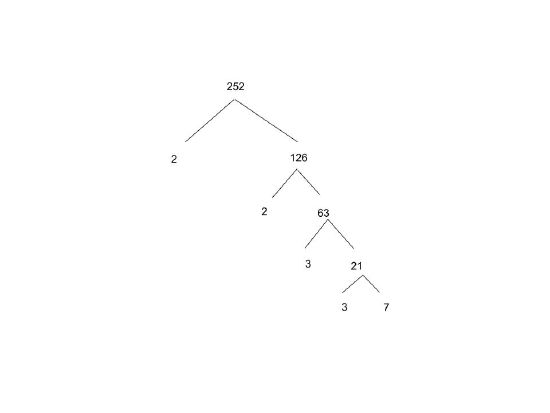
Example 6.1.6:
Find the prime factorization of
1. 252
2.2018.
3. 1000
Solution
1. Using divisibility tests, we can find that 252=22327
2. We can see that 2018 is divisible by 2, and 2018=2×1009. 1009 is prime (why?).
3. 1000=103=((2)(5))3=2353
Example 6.1.7:
Find the prime factorization of 1000001.
Solution
Consider 1000001=1000000+1=106+1=(102)3+13=(102+12)(104−102+12)=101×9901. 101 and 9901 are prime (why?)
Note: Conjectures
Goldbach's Conjecture(1742)
Every even integer n>2 is the sum of two primes.
Goldbach's Ternary Conjecture:
Every odd integer n≥5 is the sum of at most three primes.


