5.6E: Excersies
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise
For the following exercises, sketch and describe the cylindrical surface of the given equation.
1) [T]
- Answer
-
The surface is a cylinder with the rulings parallel to the y-axis.
2) [T]
3) [T]
- Answer
-
The surface is a cylinder with rulings parallel to the y-axis.
4) [T]
5) [T]
- Answer
-
The surface is a cylinder with rulings parallel to the x-axis.
6) [T]
Exercise
For the following exercises, the graph of a quadric surface is given.
a. Specify the name of the quadric surface.
b. Determine the axis of symmetry of the quadric surface.
7)
- Answer
-
a. Cylinder; b. The x-axis
8)
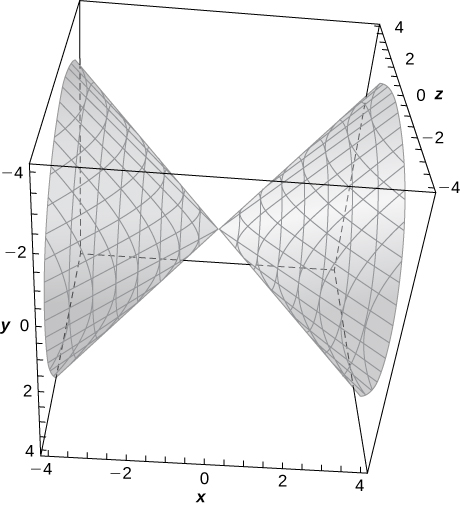
9)
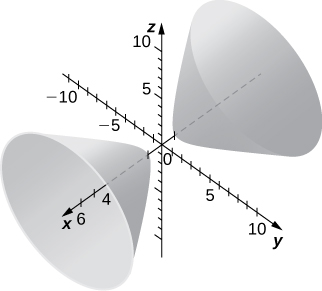
- Answer
-
a. Hyperboloid of two sheets; b. The x-axis
10)
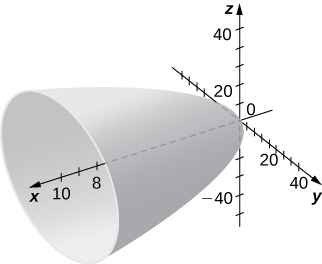
Exercise
For the following exercises, match the given quadric surface with its corresponding equation in standard form.
a.
b.
c.
d.
e.
f.
11) Hyperboloid of two sheets
- Answer
-
b.
12) Ellipsoid
13) Elliptic paraboloid
- Answer
-
d.
14) Hyperbolic paraboloid
15) Hyperboloid of one sheet
- Answer
-
a.
16) Elliptic cone
Exercise
For the following exercises, rewrite the given equation of the quadric surface in standard form. Identify the surface.
17)
- Answer
-
18)
19)
- Answer
-
20)
21)
- Answer
-
22)
23)
- Answer
-
24)
25)
- Answer
-
26)
27)
- Answer
-
28)
Exercise
For the following exercises, find the trace of the given quadric surface in the specified plane of coordinates and sketch it.
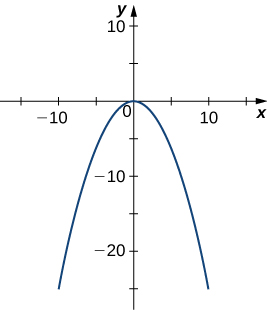
29) [T]
- Answer
-
Parabola
30) [T]
31) [T]
- Answer
-
Ellipse
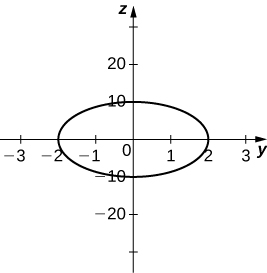
32) [T]
33) [T]
- Answer
-
Ellipse
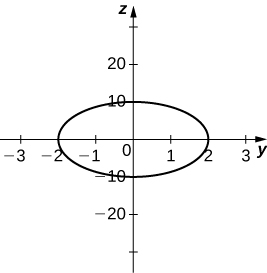
34) [T]
Exercise
35) Use the graph of the given quadric surface to answer the questions.
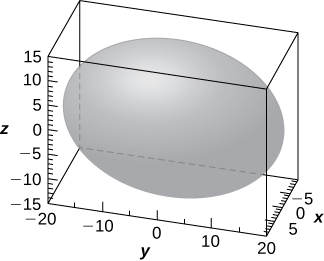
a. Specify the name of the quadric surface.
b. Which of the equations—
c. Use b. to write the equation of the quadric surface in standard form.
- Answer
-
a. Ellipsoid; b. The third equation; c.
36) Use the graph of the given quadric surface to answer the questions.
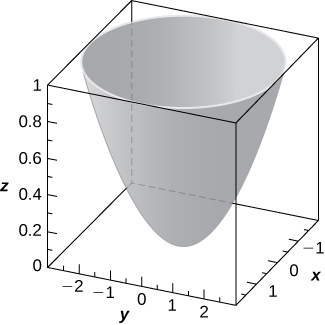
a. Specify the name of the quadric surface.
b. Which of the equations—
c. Use b. to write the equation of the quadric surface in standard form.
Exercise
For the following exercises, the equation of a quadric surface is given.
a. Use the method of completing the square to write the equation in standard form.
b. Identify the surface.
37)
- Answer
-
38)
39)
- Answer
-
40)
41)
- Answer
-
42)
Exercise
43) Write the standard form of the equation of the ellipsoid centered at the origin that passes through points
- Answer
-
44) Write the standard form of the equation of the ellipsoid centered at point
45) Determine the intersection points of elliptic cone
- Answer
-
46) Determine the intersection points of parabolic hyperboloid
47) Find the equation of the quadric surface with points
- Answer
-
48) Find the equation of the quadric surface with points
49) If the surface of a parabolic reflector is described by equation
- Answer
-
Exercise
50) Consider the parabolic reflector described by equation
51) Show that quadric surface
52) Show that quadric surface
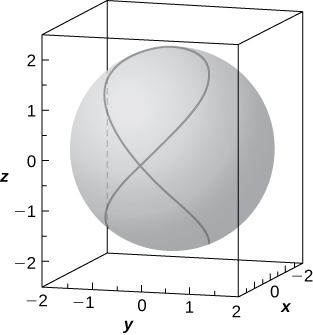
53) [T] The intersection between cylinder
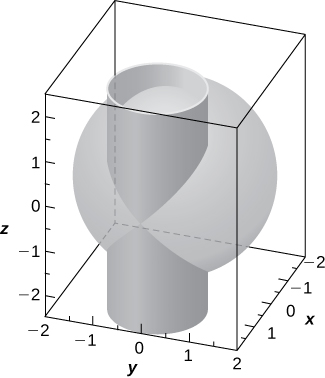
a. Solve the system consisting of the equations of the surfaces to find the equation of the intersection curve. (Hint: Find
b. Use a computer algebra system (CAS) to visualize the intersection curve on the sphere
- Answer
-
b.
54) Hyperboloid of one sheet
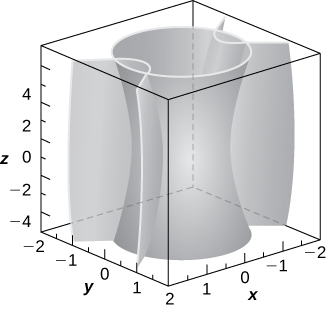
Exercise
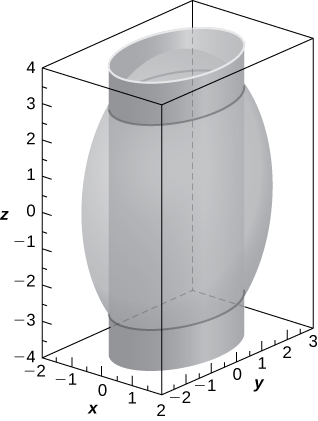
55) [T] Use a CAS to create the intersection between cylinder
- Answer
-
two ellipses of equations
56) [T] A spheroid is an ellipsoid with two equal semiaxes. For instance, the equation of a spheroid with the z-axis as its axis of symmetry is given by
a. The eye cornea is approximated as a prolate spheroid with an axis that is the eye, where
b. Give two examples of objects with prolate spheroid shapes.
57) [T] In cartography, Earth is approximated by an oblate spheroid rather than a sphere. The radii at the equator and poles are approximately
a. Write the equation in a standard form of the ellipsoid that represents the shape of Earth. Assume the center of Earth is at the origin and that the trace formed by plane
b. Sketch the graph.
c. Find the equation of the intersection curve of the surface with plane
d. Find the equation of the intersection curve of the surface with plane
- Answer
-
b.
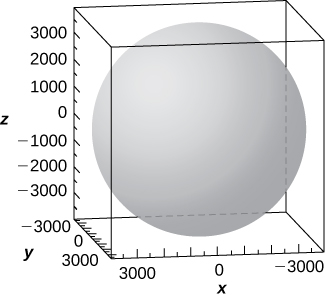
c. The intersection curve is the ellipse of equation
58) [T] A set of buzzing stunt magnets (or “rattlesnake eggs”) includes two sparkling, polished, superstrong spheroid-shaped magnets well-known for children’s entertainment. Each magnet is
a. Write the equation of the prolate spheroid centered at the origin that describes the shape of one of the magnets.
b. Write the equations of the prolate spheroids that model the shape of the buzzing stunt magnets. Use a CAS to create the graphs.
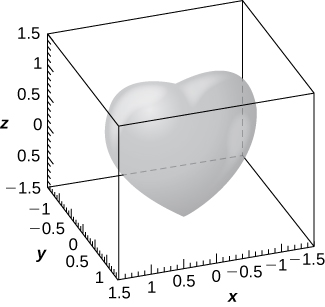
59) [T] A heart-shaped surface is given by equation
a. Use a CAS to graph the surface that models this shape.
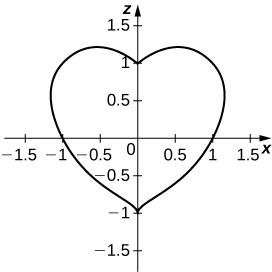
b. Determine and sketch the trace of the heart-shaped surface on the xz-plane.
- Answer
-
a.
b. The intersection curve is
60) [T] The ring torus symmetric about the z-axis is a special type of surface in topology and its equation is given by
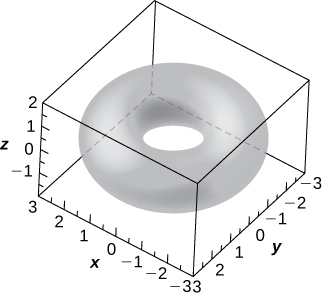
a. Write the equation of the ring torus with
b. Determine the equation and sketch the trace of the ring torus from a. on the XY-plane.
c. Give two examples of objects with ring torus shapes.

