5.7: Cylindrical and Spherical Coordinates
This page is a draft and is under active development.
( \newcommand{\kernel}{\mathrm{null}\,}\)
The Cartesian coordinate system provides a straightforward way to describe the location of points in space. Some surfaces, however, can be difficult to model with equations based on the Cartesian system. This is a familiar problem; recall that in two dimensions, polar coordinates often provide a useful alternative system for describing the location of a point in the plane, particularly in cases involving circles. In this section, we look at two different ways of describing the location of points in space, both of them based on extensions of polar coordinates. As the name suggests, cylindrical coordinates are useful for dealing with problems involving cylinders, such as calculating the volume of a round water tank or the amount of oil flowing through a pipe. Similarly, spherical coordinates are useful for dealing with problems involving spheres, such as finding the volume of domed structures.
Cylindrical Coordinates
When we expanded the traditional Cartesian coordinate system from two dimensions to three, we simply added a new axis to model the third dimension. Starting with polar coordinates, we can follow this same process to create a new three-dimensional coordinate system, called the cylindrical coordinate system. In this way, cylindrical coordinates provide a natural extension of polar coordinates to three dimensions.
Definition: The Cylindrical Coordinate System
In the cylindrical coordinate system, a point in space (Figure
( 𝑟 , 𝜃 ) 𝑥 𝑦 𝑧 𝑧
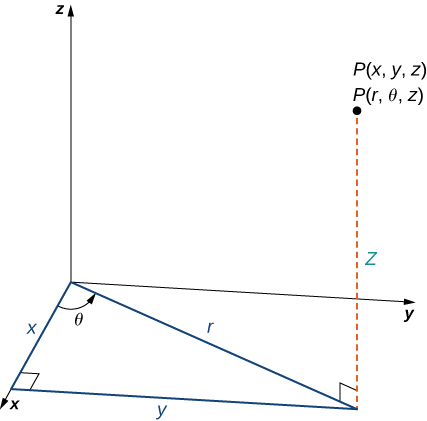
In the
Conversion between Cylindrical and Cartesian Coordinates
The rectangular coordinates
These equations are used to convert from cylindrical coordinates to rectangular coordinates.
𝑥 = 𝑟 c o s 𝜃 𝑦 = 𝑟 s i n 𝜃 𝑧 = 𝑧
These equations are used to convert from rectangular coordinates to cylindrical coordinates
𝑟 2 = 𝑥 2 + 𝑦 2 t a n 𝜃 = 𝑦 𝑥 𝑧 = 𝑧
As when we discussed conversion from rectangular coordinates to polar coordinates in two dimensions, it should be noted that the equation
Notice that these equations are derived from properties of right triangles. To make this easy to see, consider point
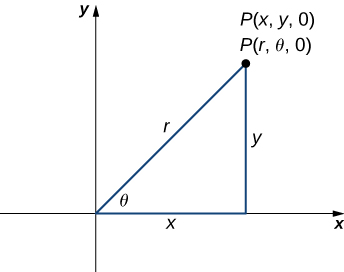
Let’s consider the differences between rectangular and cylindrical coordinates by looking at the surfaces generated when each of the coordinates is held constant. If
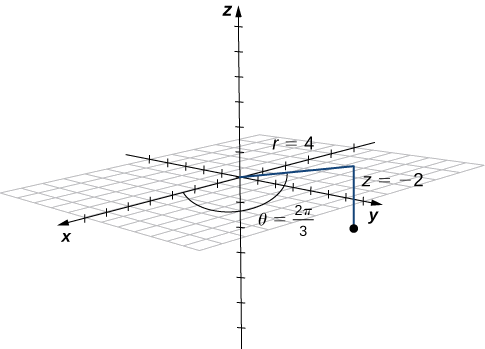
Example
Plot the point with cylindrical coordinates
Solution
Conversion from cylindrical to rectangular coordinates requires a simple application of the equations listed in Note:
The point with cylindrical coordinates
Exercise
Point
- Hint
-
The first two components match the polar coordinates of the point in the
𝑥 𝑦 - Answer
-
The rectangular coordinates of the point are
( 5 √ 3 2 , 5 2 , 4 ) . 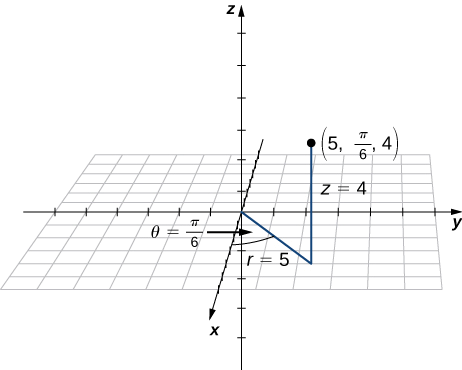
If this process seems familiar, it is with good reason. This is exactly the same process that we followed in Introduction to Parametric Equations and Polar Coordinates to convert from polar coordinates to two-dimensional rectangular coordinates.
Example
Convert the rectangular coordinates
Solution
Use the second set of equations from Note to translate from rectangular to cylindrical coordinates:
We choose the positive square root, so
In this case, the z-coordinates are the same in both rectangular and cylindrical coordinates:
The point with rectangular coordinates
Exercise
Convert point
- Hint
-
𝑟 2 = 𝑥 2 + 𝑦 2 t a n 𝜃 = 𝑦 𝑥 - Answer
-
8 √ 2 , 3 𝜋 4 , − 7 )
The use of cylindrical coordinates is common in fields such as physics. Physicists studying electrical charges and the capacitors used to store these charges have discovered that these systems sometimes have a cylindrical symmetry. These systems have complicated modeling equations in the Cartesian coordinate system, which make them difficult to describe and analyze. The equations can often be expressed in more simple terms using cylindrical coordinates. For example, the cylinder described by equation
Example
Describe the surfaces with the given cylindrical equations.
𝜃 = 𝜋 4 𝑟 2 + 𝑧 2 = 9 𝑧 = 𝑟
Solution
a. When the angle
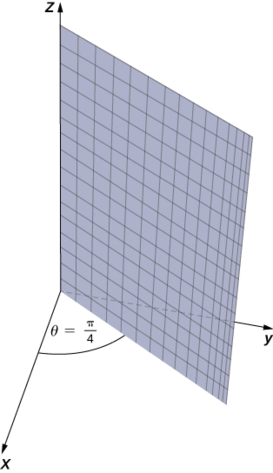
b. Substitute
c. To describe the surface defined by equation
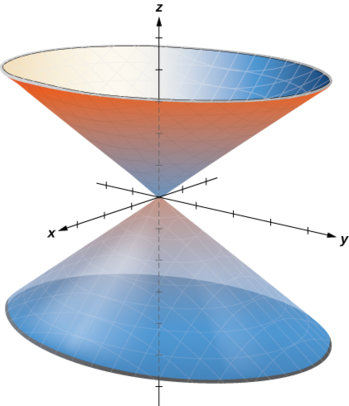
Exercise
Describe the surface with cylindrical equation
- Hint
-
The
𝜃 𝑧 - Answer
-
This surface is a cylinder with radius
6 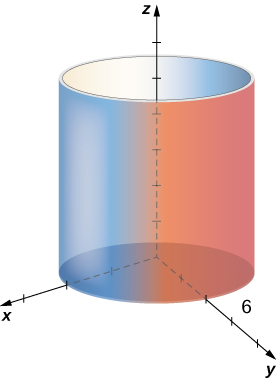
Spherical Coordinates
In the Cartesian coordinate system, the location of a point in space is described using an ordered triple in which each coordinate represents a distance. In the cylindrical coordinate system, location of a point in space is described using two distances
Definition: spherical coordinate system
In the spherical coordinate system, a point
𝜌 𝑃 ( 𝜌 ≠ 0 ) ; 𝜃 𝜑 𝑧 ¯ 𝑂 𝑃 𝑂 0 ≤ 𝜑 ≤ 𝜋 .
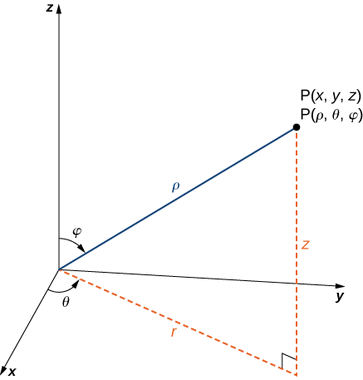
By convention, the origin is represented as
HOWTO: Converting among Spherical, Cylindrical, and Rectangular Coordinates
Rectangular coordinates
Convert from spherical coordinates to rectangular coordinates
These equations are used to convert from spherical coordinates to rectangular coordinates.
𝑥 = 𝜌 s i n 𝜑 𝑐 𝑜 𝑠 𝜃 𝑦 = 𝜌 s i n 𝜑 s i n 𝜃 𝑧 = 𝜌 c o s 𝜑
Convert from rectangular coordinates to spherical coordinates
These equations are used to convert from rectangular coordinates to spherical coordinates.
𝜌 2 = 𝑥 2 + 𝑦 2 + 𝑧 2 t a n 𝜃 = 𝑦 𝑥 𝜑 = a r c c o s ( 𝑧 √ 𝑥 2 + 𝑦 2 + 𝑧 2 ) .
Convert from spherical coordinates to rectangular coordinates
These equations are used to convert from spherical coordinates to rectangular coordinates.
𝑟 = 𝜌 s i n 𝜑 𝜃 = 𝜃 𝑧 = 𝜌 c o s 𝜑
Convert from cylindrical coordinates to spherical coordinates
These equations are used to convert from cylindrical coordinates to spherical coordinates.
𝜌 = √ 𝑟 2 + 𝑧 2 𝜃 = 𝜃 𝜑 = a r c c o s ( 𝑧 √ 𝑟 2 + 𝑧 2 )
The formulas to convert from spherical coordinates to rectangular coordinates may seem complex, but they are straightforward applications of trigonometry. Looking at Figure, it is easy to see that
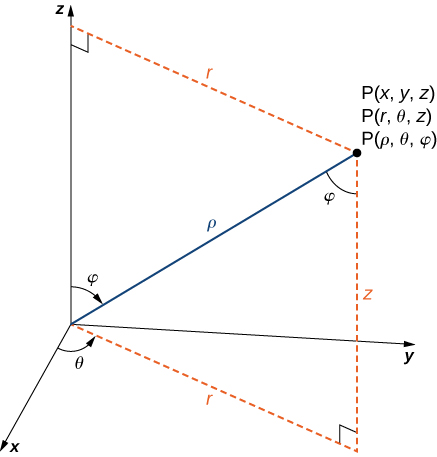
As we did with cylindrical coordinates, let’s consider the surfaces that are generated when each of the coordinates is held constant. Let
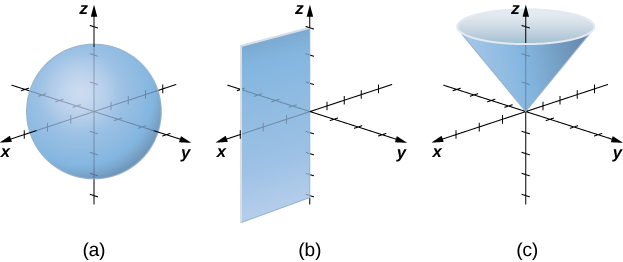
Example
Plot the point with spherical coordinates
Solution
Use the equations in Note to translate between spherical and cylindrical coordinates (Figure
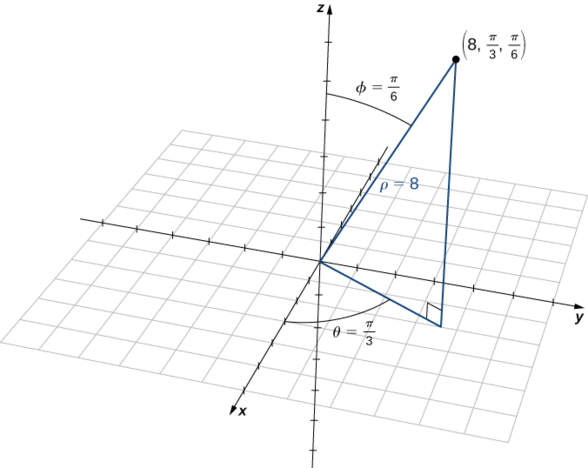
The point with spherical coordinates
Finding the values in cylindrical coordinates is equally straightforward:
Thus, cylindrical coordinates for the point are
Exercise
Plot the point with spherical coordinates
- Hint
-
Converting the coordinates first may help to find the location of the point in space more easily.
- Answer
-
Cartesian:
( − √ 3 2 , − 1 2 , √ 3 ) , ( 1 , − 5 𝜋 6 , √ 3 ) 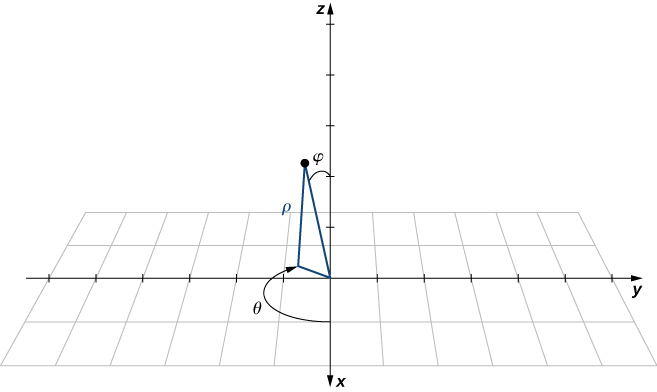
Example
Convert the rectangular coordinates
Solution
Start by converting from rectangular to spherical coordinates:
Because
There are actually two ways to identify
and therefore
To find the cylindrical coordinates for the point, we need only find r:
The cylindrical coordinates for the point are
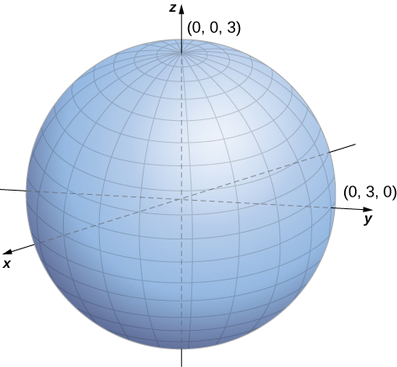
Example
Describe the surfaces with the given spherical equations.
𝜃 = 𝜋 3 𝜑 = 5 𝜋 6 𝜌 = 6 𝜌 = s i n 𝜃 𝑠 𝑖 𝑛 𝜑
Solution
a. The variable
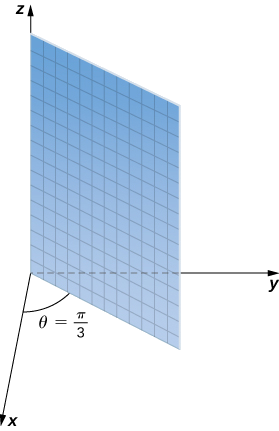
b. Equation
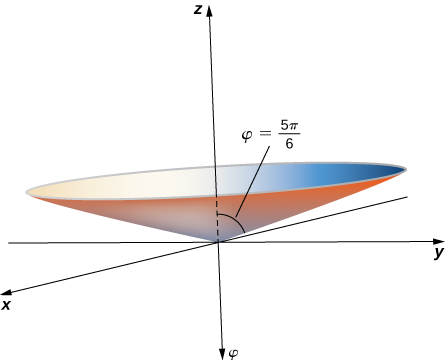
To find the equation in rectangular coordinates, use equation
This is the equation of a cone centered on the
c. Equation
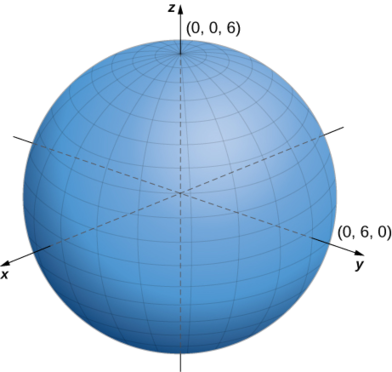
d. To identify this surface, convert the equation from spherical to rectangular coordinates, using equations
The equation describes a sphere centered at point
Exercise
Describe the surfaces defined by the following equations.
𝜌 = 1 3 𝜃 = 2 𝜋 3 𝜑 = 𝜋 4
- Hint
-
Think about what each component represents and what it means to hold that component constant.
- Answer a
-
This is the set of all points
1 3 1 3 - Answer b
-
This set of points forms a half plane. The angle between the half plane and the positive
𝑥 𝜃 = 2 𝜋 3 . - Answer c
-
Let
𝑃 𝜑 = 𝜋 4 𝑧
Spherical coordinates are useful in analyzing systems that have some degree of symmetry about a point, such as the volume of the space inside a domed stadium or wind speeds in a planet’s atmosphere. A sphere that has Cartesian equation
In geography, latitude and longitude are used to describe locations on Earth’s surface, as shown in Figure. Although the shape of Earth is not a perfect sphere, we use spherical coordinates to communicate the locations of points on Earth. Let’s assume Earth has the shape of a sphere with radius
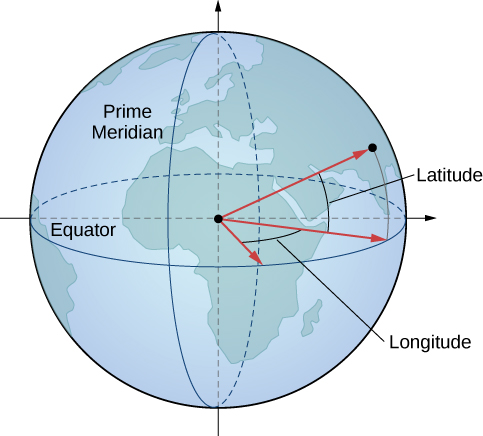
Let the center of Earth be the center of the sphere, with the ray from the center through the North Pole representing the positive
Example
The latitude of Columbus, Ohio, is
Solution
The radius of Earth is
Exercise
Sydney, Australia is at
- Hint
-
Because Sydney lies south of the equator, we need to add
9 0 ° 𝑧 - Answer
-
( 4 0 0 0 , 1 5 1 ° , 1 2 4 ° )
Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. A thoughtful choice of coordinate system can make a problem much easier to solve, whereas a poor choice can lead to unnecessarily complex calculations. In the following example, we examine several different problems and discuss how to select the best coordinate system for each one.
Example
In each of the following situations, we determine which coordinate system is most appropriate and describe how we would orient the coordinate axes. There could be more than one right answer for how the axes should be oriented, but we select an orientation that makes sense in the context of the problem. Note: There is not enough information to set up or solve these problems; we simply select the coordinate system (Figure
- Find the center of gravity of a bowling ball.
- Determine the velocity of a submarine subjected to an ocean current.
- Calculate the pressure in a conical water tank.
- Find the volume of oil flowing through a pipeline.
- Determine the amount of leather required to make a football.

Solution
- Clearly, a bowling ball is a sphere, so spherical coordinates would probably work best here. The origin should be located at the physical center of the ball. There is no obvious choice for how the
𝑥 𝑦 𝑧 𝑧 - A submarine generally moves in a straight line. There is no rotational or spherical symmetry that applies in this situation, so rectangular coordinates are a good choice. The
𝑧 𝑥 𝑦 - A cone has several kinds of symmetry. In cylindrical coordinates, a cone can be represented by equation
𝑧 = 𝑘 𝑟 , 𝑘 𝜑 = 𝑐 𝑧 2 = 𝑥 2 𝑎 2 + 𝑦 2 𝑏 2 . 𝑧 - A pipeline is a cylinder, so cylindrical coordinates would be best the best choice. In this case, however, we would likely choose to orient our
𝑧 𝑥 𝑧 - A football has rotational symmetry about a central axis, so cylindrical coordinates would work best. The
𝑧 𝑥
Exercise
Which coordinate system is most appropriate for creating a star map, as viewed from Earth (see the following figure)?
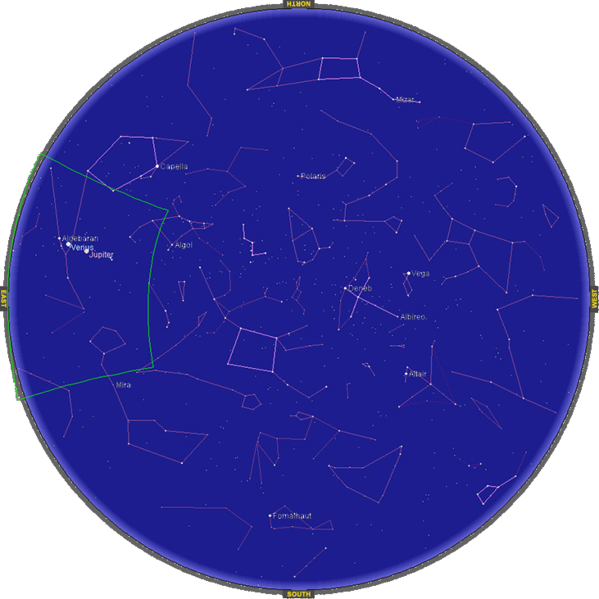
How should we orient the coordinate axes?
- Hint
-
What kinds of symmetry are present in this situation?
- Answer
-
Spherical coordinates with the origin located at the center of the earth, the
𝑧 𝑥
Key Concepts
- In the cylindrical coordinate system, a point in space is represented by the ordered triple
( 𝑟 , 𝜃 , 𝑧 ) , ( 𝑟 , 𝜃 ) 𝑥 𝑦 𝑧 - To convert a point from cylindrical coordinates to Cartesian coordinates, use equations
𝑥 = 𝑟 c o s 𝜃 , 𝑦 = 𝑟 s i n 𝜃 , 𝑧 = 𝑧 . - To convert a point from Cartesian coordinates to cylindrical coordinates, use equations
𝑟 2 = 𝑥 2 + 𝑦 2 , t a n 𝜃 = 𝑦 𝑥 , 𝑧 = 𝑧 . - In the spherical coordinate system, a point
𝑃 ( 𝜌 , 𝜃 , 𝜑 ) 𝜌 𝑃 ( 𝜌 ≠ 0 ) , 𝜃 𝜑 𝑧 ¯ 𝑂 𝑃 𝑂 0 ≤ 𝜑 ≤ 𝜋 . - To convert a point from spherical coordinates to Cartesian coordinates, use equations
𝑥 = 𝜌 s i n 𝜑 c o s 𝜃 , 𝑦 = 𝜌 s i n 𝜑 s i n 𝜃 , 𝑧 = 𝜌 c o s 𝜑 . - To convert a point from Cartesian coordinates to spherical coordinates, use equations
𝜌 2 = 𝑥 2 + 𝑦 2 + 𝑧 2 , t a n 𝜃 = 𝑦 𝑥 , 𝜑 = a r c c o s ( 𝑧 √ 𝑥 2 + 𝑦 2 + 𝑧 2 ) - To convert a point from spherical coordinates to cylindrical coordinates, use equations
𝑟 = 𝜌 s i n 𝜑 , 𝜃 = 𝜃 , 𝑧 = 𝜌 c o s 𝜑 . - To convert a point from cylindrical coordinates to spherical coordinates, use equations
𝜌 = √ 𝑟 2 + 𝑧 2 , 𝜃 = 𝜃 , 𝜑 = a r c c o s ( 𝑧 √ 𝑟 2 + 𝑧 2 ) .
Glossary
- cylindrical coordinate system
- a way to describe a location in space with an ordered triple
( 𝑟 , 𝜃 , 𝑧 ) , ( 𝑟 , 𝜃 ) 𝑥 𝑦 𝑧
- spherical coordinate system
- a way to describe a location in space with an ordered triple
( 𝜌 , 𝜃 , 𝜑 ) , 𝜌 𝑃 ( 𝜌 ≠ 0 ) , 𝜃 𝜑 𝑧 ¯ 𝑂 𝑃 𝑂 0 ≤ 𝜑 ≤ 𝜋
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
- Paul Seeburger edited the LaTeX on the page

