4.1 E: Exercises
This page is a draft and is under active development.
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise \PageIndex{1}
Find the first six terms of each of the following sequences, starting with \displaystyle n=1.
1) \displaystyle a_n=1+(−1)^n for \displaystyle n≥1
- Answer
-
Solution: \displaystyle a_n=0 if \displaystyle n is odd and \displaystyle a_n=2 if \displaystyle n is even
2) \displaystyle a_n=n^2−1 for \displaystyle n≥1
3) \displaystyle a_1=1 and \displaystyle a_n=a_{n−1}+n for \displaystyle n≥2
- Answer
-
Solution: \displaystyle {a_n}={1,3,6,10,15,21,…}
4) \displaystyle a_1=1, a_2=1 and \displaystyle a_n+2=a_n+a_{n+1} for \displaystyle n≥1
Exercise \PageIndex{2}
1) Find an explicit formula for \displaystyle a_n where \displaystyle a_1=1 and \displaystyle a_n=a_{n−1}+n for \displaystyle n≥2.
- Answer
-
\displaystyle a_n=\frac{n(n+1)}{2}
2) Find a formula \displaystyle a_n for the \displaystyle nth term of the arithmetic sequence whose first term is \displaystyle a_1=1 such that \displaystyle a_{n−1}−a_n=17 for \displaystyle n≥1.
3) Find a formula \displaystyle a_n for the \displaystyle nth term of the arithmetic sequence whose first term is \displaystyle a_1=−3 such that \displaystyle a_{n−1}−a_n=4 for \displaystyle n≥1.
- Answer
-
\displaystyle a_n=4n−7
4) Find a formula \displaystyle a_n for the \displaystyle nth term of the geometric sequence whose first term is \displaystyle a_1=1 such that \displaystyle \frac{a_{n+1}}{a_n}=10 for \displaystyle n≥1.
5) Find a formula \displaystyle a_n for the \displaystyle nth term of the geometric sequence whose first term is \displaystyle a_1=3 such that \displaystyle \frac{a_{n+1}}{a_n}=1/10 for \displaystyle n≥1.
- Answer
-
Solution: \displaystyle a_n=3.10^{1−n}=30.10^{−n}
6) Find an explicit formula for the \displaystyle nth term of the sequence whose first several terms are \displaystyle {0,3,8,15,24,35,48,63,80,99,…}. (Hint: First add one to each term.)
7) Find an explicit formula for the \displaystyle nth term of the sequence satisfying \displaystyle a_1=0 and \displaystyle a_n=2a_{n−1}+1 for \displaystyle n≥2.
- Answer
-
Solution: \displaystyle a_n=2^n−1
Find a formula for the general term \displaystyle a_n of each of the following sequences.
8) \displaystyle {1,0,−1,0,1,0,−1,0,…} (Hint: Find where \displaystyle sinx takes these values)
9) \displaystyle {1,−1/3,1/5,−1/7,…}
- Answer
-
Solution: \displaystyle a_n=\frac{(−1)^{n−1}}{2n−1}
Exercise \PageIndex{3}
Find a function \displaystyle f(n) that identifies the \displaystyle nth term \displaystyle a_n of the following recursively defined sequences, as \displaystyle a_n=f(n).
1) \displaystyle a_1=1 and \displaystyle a_{n+1}=−a_n for \displaystyle n≥1
2) \displaystyle a_1=2 and \displaystyle a_{n+1}=2a_n for \displaystyle n≥1
- Answer
-
Solution: \displaystyle f(n)=2^n
3) \displaystyle a_1=1 and \displaystyle a_{n+1}=(n+1)a_n for \displaystyle n≥1
4) \displaystyle a_1=2 and \displaystyle a_{n+1}=(n+1)a_n/2 for \displaystyle n≥1
Answer
-
Solution: \displaystyle a_1=1 and \displaystyle a_{n+1}=a_n/2^n for \displaystyle n≥1
Exercise \PageIndex{4}
Plot the first \displaystyle N terms of each sequence. State whether the graphical evidence suggests that the sequence converges or diverges.
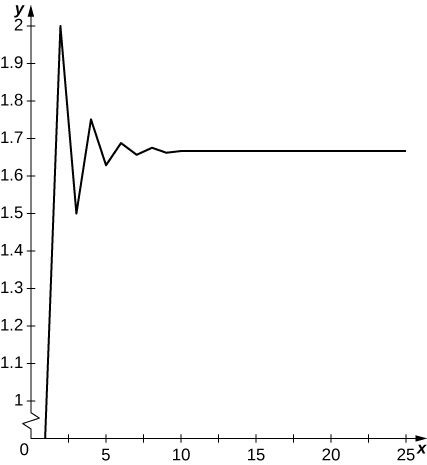
1) [T] \displaystyle a_1=1, a_2=2, and for \displaystyle n≥2, a_n=\frac{1}{2}(a_{n−1}+a_{n−2}); \displaystyle N=30
- Answer
-
Solution: Terms oscillate above and below \displaystyle 5/3 and appear to converge to \displaystyle 5/3.
2) [T] \displaystyle a_1=1, a_2=2, a_3=3 and for \displaystyle n≥4, a_n=\frac{1}{3}(a_{n−1}+a_{n−2}+a_{n−3}), N=30
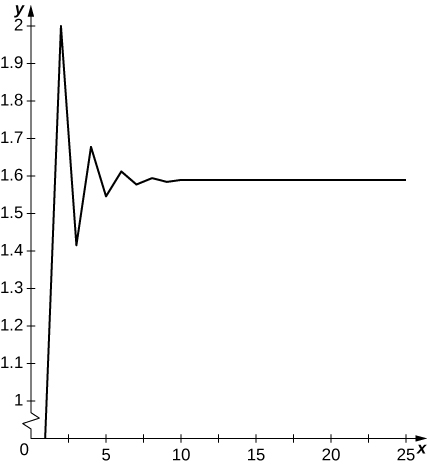
3) [T] \displaystyle a_1=1, a_2=2, and for \displaystyle n≥3, a_n=\sqrt{a_{n−1}a_{n−2}}; N=30
- Answer
-
Solution: Terms oscillate above and below \displaystyle y≈1.57.. and appear to converge to a limit.
4) [T] \displaystyle a_1=1, a_2=2, a_3=3, and for \displaystyle n≥4, a_n=\sqrt{a_{n−1}a_{n−2}a_{n−3}}; N=30
Exercise \PageIndex{5}
Suppose that \displaystyle \lim_{n→∞}a_n=1, \lim_{n→∞}b_n=−1, and \displaystyle 0<−b_n<a_n for all \displaystyle n. Evaluate each of the following limits, or state that the limit does not exist, or state that there is not enough information to determine whether the limit exists.
1) \displaystyle \lim_{n→∞}3a_n−4b_n
- Answer
-
Solution: \displaystyle 7
2) \displaystyle \lim_{n→∞}\frac{1}{2}b_n−\frac{1}{2}a_n
3) \displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n}
- Answer
-
Solution: \displaystyle 0
4) \displaystyle \lim_{n→∞}\frac{a_n−b_n}{a_n+b_n}
Exercise \PageIndex{6}
Find the limit of each of the following sequences, using L’Hôpital’s rule when appropriate.
1) \displaystyle \frac{n^2}{2^n}
- Answer
-
Solution: \displaystyle 0
2) \displaystyle \frac{(n−1)^2}{(n+1)^2}
3) \displaystyle \frac{\sqrt{n}}{\sqrt{n+1}}
- Answer
-
Solution: \displaystyle 1
4) \displaystyle n^{1/n} (Hint: \displaystyle n^{1/n}=e^{\frac{1}{n}lnn})
Exercise \PageIndex{7}
For each of the following sequences, whose \displaystyle nth terms are indicated, state whether the sequence is bounded and whether it is eventually monotone, increasing, or decreasing.
1) \displaystyle n/2^n, n≥2
- Answer
-
Solution: bounded, decreasing for \displaystyle n≥1
2) \displaystyle ln(1+\frac{1}{n})
3) \displaystyle sinn
- Answer
-
Solution: bounded, not monotone
4) \displaystyle cos(n^2)
5) \displaystyle n^{1/n}, n≥3
- Answer
-
Solution: bounded, decreasing
6) \displaystyle n^{−1/n}, n≥3
7) \displaystyle tan(n)
- Answer
-
Solution: not monotone, not bounded
Exercise \PageIndex{8}
Determine whether the sequence defined as follows has a limit. If it does, find the limit.
1) \displaystyle a_1=\sqrt{2}, a_2=\sqrt{2\sqrt{2}}. a_3=\sqrt{2\sqrt{2\sqrt{2}}} etc.
2) \displaystyle a_1=3, a_n=\sqrt{2a_{n−1}}, n=2,3,….
- Answer
-
Solution: \displaystyle a-n is decreasing and bounded below by \displaystyle 2. The limit a must satisfy \displaystyle a=\sqrt{2a} so \displaystyle a=2, independent of the initial value.
Exercise \PageIndex{9}
Use the Squeeze Theorem to find the limit of each of the following sequences.
1) \displaystyle nsin(1/n)
2) \displaystyle \frac{cos(1/n)−1}{1/n}
- Answer
-
Solution: \displaystyle 0
3) \displaystyle a_n=\frac{n!}{n^n}
4) \displaystyle a_n=sinnsin(1/n)
- Answer
-
Solution: \displaystyle 0:|sinx|≤|x| and \displaystyle |sinx|≤1 so \displaystyle −\frac{1}{n}≤a_n≤\frac{1}{n}).
Exercise \PageIndex{10}
For the following sequences, plot the first \displaystyle 25 terms of the sequence and state whether the graphical evidence suggests that the sequence converges or diverges.
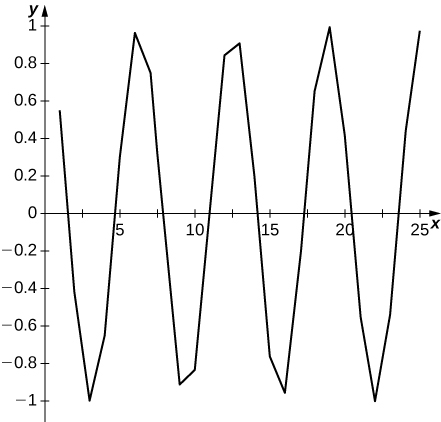
1) [T] \displaystyle a_n=sinn
2) [T] \displaystyle a_n=cosn
- Answer
-
Solution: Graph oscillates and suggests no limit.
Exercise \PageIndex{11}
Determine the limit of the sequence or show that the sequence diverges. If it converges, find its limit.
1) \displaystyle a_n=tan^{−1}(n^2)
2) \displaystyle a_n=(2n)^{1/n}−n^{1/n}
- Answer
-
Solution: \displaystyle n^{1/n}→1 and \displaystyle 2^{1/n}→1, so \displaystyle a_n→0
3) \displaystyle a_n=\frac{ln(n^2)}{ln(2n)}
4) \displaystyle a_n=(1−\frac{2}{n})^n
- Answer
-
Solution: Since \displaystyle (1+1/n)^n→e, one has \displaystyle (1−2/n)^n≈(1+k)^{−2k}→e^{−2} as \displaystyle k→∞.
5) \displaystyle a_n=ln(\frac{n+2}{n^2−3})
6) \displaystyle a_n=\frac{2^n+3^n}{4^n}
- Answer
-
Solution: \displaystyle 2^n+3^n≤2⋅3^n and \displaystyle 3^n/4^n→0 as \displaystyle n→∞, so \displaystyle a_n→0 as \displaystyle n→∞.
7) \displaystyle a_n=\frac{(1000)^n}{n!}
8) \displaystyle a_n=\frac{(n!)^2}{(2n)!}
- Answer
-
Solution: \displaystyle \frac{a_{n+1}}{a_n}=n!/(n+1)(n+2)⋯(2n) =\frac{1⋅2⋅3⋯n}{(n+1)(n+2)⋯(2n)}<1/2^n. In particular, \displaystyle a_{n+1}/a_n≤1/2, so \displaystyle a_n→0 as \displaystyle n→∞
Exercise \PageIndex{12}
Newton’s method seeks to approximate a solution \displaystyle f(x)=0 that starts with an initial approximation \displaystyle x_0 and successively defines a sequence \displaystyle x_{n+1}=x_n−\frac{f(x_n)}{f′(x_n)}. For the given choice of \displaystyle f and \displaystyle x_0, write out the formula for \displaystyle x_{n+1}. If the sequence appears to converge, give an exact formula for the solution \displaystyle x, then identify the limit \displaystyle x accurate to four decimal places and the smallest \displaystyle n such that \displaystyle x_n agrees with \displaystyle x up to four decimal places.
1) [T] \displaystyle f(x)=x^2−2, x_0=1
2) [T] \displaystyle f(x)=(x−1)^2−2, x_0=2
- Answer
-
Solution: \displaystyle x_{n+1}=x_n−((x_n−1)^2−2)/2(x_n−1); x=1+\sqrt{2}, x≈2.4142, n=5
3) [T] \displaystyle f(x)=e^x−2, x_0=1
4) [T] \displaystyle f(x)=lnx−1, x_0=2
- Answer
-
Solution: \displaystyle x_{n+1}=x_n−x_n(ln(x_n)−1); x=e, x≈2.7183, n=5
Exercise \PageIndex{13}
1) [T] Suppose you start with one liter of vinegar and repeatedly remove \displaystyle 0.1L, replace with water, mix, and repeat.
a. Find a formula for the concentration after \displaystyle n steps.
b. After how many steps does the mixture contain less than \displaystyle 10% vinegar?
2) [T] A lake initially contains \displaystyle 2000 fish. Suppose that in the absence of predators or other causes of removal, the fish population increases by \displaystyle 6% each month. However, factoring in all causes, \displaystyle 150 fish are lost each month.
a. Explain why the fish population after \displaystyle n months is modeled by \displaystyle P_n=1.06P_{n−1}−150 with \displaystyle P_0=2000.
b. How many fish will be in the pond after one year?
- Answer
-
Solution: a. Without losses, the population would obey \displaystyle P_n=1.06P_{n−1}. The subtraction of \displaystyle 150 accounts for fish losses. b. After \displaystyle 12 months, we have \displaystyle P_{12}≈1494.
3) [T] A bank account earns \displaystyle 5% interest compounded monthly. Suppose that \displaystyle $1000 is initially deposited into the account, but that \displaystyle $10 is withdrawn each month.
a. Show that the amount in the account after \displaystyle n months is \displaystyle A_n=(1+.05/12)A_{n−1}−10; A_0=1000.
b. How much money will be in the account after \displaystyle 1 year?
c. Is the amount increasing or decreasing?
d. Suppose that instead of \displaystyle $10, a fixed amount \displaystyle d dollars is withdrawn each month. Find a value of \displaystyle d such that the amount in the account after each month remains \displaystyle $1000.
e. What happens if \displaystyle d is greater than this amount?
4) [T] A student takes out a college loan of \displaystyle $10,000 at an annual percentage rate of \displaystyle 6%, compounded monthly.
a. If the student makes payments of \displaystyle $100 per month, how much does the student owe after \displaystyle 12 months?
b. After how many months will the loan be paid off?
- Answer
-
Solution: a. The student owes \displaystyle $9383 after \displaystyle 12 months. b. The loan will be paid in full after \displaystyle 139 months or eleven and a half years.
5) [T] Consider a series combining geometric growth and arithmetic decrease. Let \displaystyle a_1=1. Fix \displaystyle a>1 and \displaystyle 0<b<a. Set \displaystyle a_{n+1}=a.a_n−b. Find a formula for \displaystyle a_{n+1} in terms of \displaystyle a_n, a, and \displaystyle b and a relationship between \displaystyle a and \displaystyle b such that \displaystyle a_n converges.
6) [T] The binary representation \displaystyle x=0.b_1b_2b_3... of a number \displaystyle x between \displaystyle 0 and \displaystyle 1 can be defined as follows. Let \displaystyle b_1=0 if \displaystyle x<1/2 and \displaystyle b_1=1 if \displaystyle 1/2≤x<1. Let \displaystyle x_1=2x−b_1. Let \displaystyle b_2=0 if \displaystyle x_1<1/2 and \displaystyle b_2=1 if \displaystyle 1/2≤x<1. Let \displaystyle x_2=2x_1−b_2 and in general, \displaystyle x_n=2x_{n−1}−b_n and \displaystyle b_{n−}1=0 if \displaystyle x_n<1/2 and \displaystyle b_{n−1}=1 if \displaystyle 1/2≤x_n<1. Find the binary expansion of \displaystyle 1/3.
- Answer
-
Solution: \displaystyle b_1=0, x_1=2/3, b_2=1, x_2=4/3−1=1/3, so the pattern repeats, and \displaystyle 1/3=0.010101….
7) [T] To find an approximation for \displaystyle π, set \displaystyle a_0=\sqrt{2+1}, a_1=\sqrt{2+a_0}, and, in general, \displaystyle a_{n+1}=\sqrt{2+a_n}. Finally, set \displaystyle p_n=3.2^n\sqrt{2−a_n}. Find the first ten terms of \displaystyle p_n and compare the values to \displaystyle π.
Exercise \PageIndex{14}
For the following two exercises, assume that you have access to a computer program or Internet source that can generate a list of zeros and ones of any desired length. Pseudorandom number generators (PRNGs) play an important role in simulating random noise in physical systems by creating sequences of zeros and ones that appear like the result of flipping a coin repeatedly. One of the simplest types of PRNGs recursively defines a random-looking sequence of \displaystyle N integers \displaystyle a_1,a_2,…,a_N by fixing two special integers \displaystyle (K and \displaystyle M and letting \displaystyle a_{n+1} be the remainder after dividing \displaystyle K.a_n into \displaystyle M, then creates a bit sequence of zeros and ones whose \displaystyle nth term \displaystyle b_n is equal to one if \displaystyle a_n is odd and equal to zero if \displaystyle a_n is even. If the bits \displaystyle b_n are pseudorandom, then the behavior of their average \displaystyle (b_1+b_2+⋯+b_N)/N should be similar to behavior of averages of truly randomly generated bits.
1) [T] Starting with \displaystyle K=16,807 and \displaystyle M=2,147,483,647, using ten different starting values of \displaystyle a_1, compute sequences of bits \displaystyle b_n up to \displaystyle n=1000, and compare their averages to ten such sequences generated by a random bit generator.
- Answer
-
Solution: For the starting values \displaystyle a_1=1, a_2=2,…, a_1=10, the corresponding bit averages calculated by the method indicated are \displaystyle 0.5220, 0.5000, 0.4960, 0.4870, 0.4860, 0.4680, 0.5130, 0.5210, 0.5040, and \displaystyle 0.4840. Here is an example of ten corresponding averages of strings of \displaystyle 1000 bits generated by a random number generator: \displaystyle 0.4880, 0.4870, 0.5150, 0.5490, 0.5130, 0.5180, 0.4860, 0.5030, 0.5050, 0.4980. There is no real pattern in either type of average. The random-number-generated averages range between \displaystyle 0.4860 and \displaystyle 0.5490, a range of \displaystyle 0.0630, whereas the calculated PRNG bit averages range between \displaystyle 0.4680 and \displaystyle 0.5220, a range of \displaystyle 0.0540.
2) [T] Find the first \displaystyle 1000 digits of \displaystyle π using either a computer program or Internet resource. Create a bit sequence \displaystyle b_n by letting \displaystyle b_n=1 if the \displaystyle nth digit of \displaystyle π is odd and \displaystyle b_n=0 if the \displaystyle nth digit of \displaystyle π is even. Compute the average value of \displaystyle b_n and the average value of \displaystyle d_n=|b_{n+1}−b_n|, n=1,...,999. Does the sequence \displaystyle b_n appear random? Do the differences between successive elements of \displaystyle b_n appear random?
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

