1.3E: Exercises

Last updated
Save as PDF

Page ID: 17136

This page is a draft and is under active development.

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Exercise $\PageIndex{1}$

In the following exercises, find the Taylor polynomials of degree two approximating the given function centered at the given point.

1. $\displaystyle f(x)=1+x+x^2$ at $\displaystyle a=1$

2. $\displaystyle f(x)=1+x+x^2$ at $\displaystyle a=−1$

Answer: $\displaystyle f(−1)=1;f′(−1)=−1;f''(−1)=2;f(x)=1−(x+1)+(x+1)^2$

3. $\displaystyle f(x)=cos(2x)$ at $\displaystyle a=π$

4. $\displaystyle f(x)=sin(2x)$ at $\displaystyle a=\frac{π}{2}$

Answer: $\displaystyle f′(x)=2cos(2x);f''(x)=−4sin(2x);p_2(x)=−2(x−\frac{π}{2})$

5. $\displaystyle f(x)=\sqrt{x}$ at $\displaystyle a=4$

6. $\displaystyle f(x)=lnx$ at $\displaystyle a=1$

Answer: $\displaystyle f′(x)=\frac{1}{x};f''(x)=−\frac{1}{x^2};p_2(x)=0+(x−1)−\frac{1}{2}(x−1)^2$

7. $\displaystyle f(x)=\frac{1}{x}$ at $\displaystyle a=1$

8. $\displaystyle f(x)=e^x$ at $\displaystyle a=1$

Answer: $\displaystyle p_2(x)=e+e(x−1)+\frac{e}{2}(x−1)^2$

Exercise $\PageIndex{2}$

In the following exercises, verify that the given choice of n in the remainder estimate $\displaystyle |R_n|≤\frac{M}{(n+1)!}(x−a)^{n+1}$, where M is the maximum value of $\displaystyle ∣f^{(n+1)}(z)∣$ on the interval between a and the indicated point, yields $\displaystyle |R_n|≤\frac{1}{1000}$. Find the value of the Taylor polynomial $\displaystyle p_n$ of $\displaystyle f$ at the indicated point.

1. (\displaystyle \sqrt{10};a=9,n=3\)

2. $\displaystyle (28)^{1/3};a=27,n=1$

Answer: $\displaystyle \frac{d^2}{dx^2}x^{1/3}=−\frac{2}{9x^{5/3}}≥−0.00092…$ when $\displaystyle x≥28$ so the remainder estimate applies to the linear approximation $\displaystyle x^{1/3}≈p_1(27)=3+\frac{x−27}{27}$, which gives $\displaystyle (28)^{1/3}≈3+\frac{1}{27}=3.\bar{037}$, while $\displaystyle (28)^{1/3}≈3.03658.$

3. $\displaystyle sin(6);a=2π,n=5$

4. $\displaystyle e^2; a=0,n=9$

Answer: Using the estimate $\displaystyle \frac{2^{10}}{10!}<0.000283$ we can use the Taylor expansion of order 9 to estimate $\displaystyle e^x$ at $\displaystyle x=2$. as $\displaystyle e^2≈p_9(2)=1+2+\frac{2^2}{2}+\frac{2^3}{6}+⋯+\frac{2^9}{9!}=7.3887$… whereas $\displaystyle e^2≈7.3891.$

5. $\displaystyle cos(\frac{π}{5});a=0,n=4$

6. $\displaystyle ln(2);a=1,n=1000$

Answer: Since $\displaystyle \frac{d^n}{dx^n}(lnx)=(−1)^{n−1}\frac{(n−1)!}{x^n},R_{1000}≈\frac{1}{1001}$. One has $\displaystyle p_{1000}(1)=\sum_{n=1}^{1000}\frac{(−1)^{n−1}}{n}≈0.6936$ whereas $\displaystyle ln(2)≈0.6931⋯.$

Exercise $\PageIndex{3}$

1. Integrate the approximation $\displaystyle sint≈t−\frac{t^3}{6}+\frac{t^5}{120}−\frac{t^7}{5040}$ evaluated at $\displaystyle π$t to approximate $\displaystyle ∫^1_0\frac{sinπt}{πt}dt$.

2. Integrate the approximation $\displaystyle e^x≈1+x+\frac{x^2}{2}+⋯+\frac{x^6}{720}$ evaluated at $\displaystyle −x^2$ to approximate $\displaystyle ∫^1_0e^{−x^2}dx.$

Answer: $\displaystyle ∫^1_0(1−x^2+\frac{x^4}{2}−\frac{x^6}{6}+\frac{x^8}{24}−\frac{x^{10}}{120}+\frac{x^{12}}{720})dx =1−\frac{1^3}{3}+\frac{1^5}{10}−\frac{1^7}{42}+\frac{1^9}{9⋅24}−\frac{1^{11}}{120⋅11}+\frac{1^{13}}{720⋅13}≈0.74683$ whereas $\displaystyle ∫^1_0e^{−x^2}dx≈0.74682.$

Exercise $\PageIndex{4}$

In the following exercises, find the smallest value of n such that the remainder estimate $\displaystyle |R_n|≤\frac{M}{(n+1)!}(x−a)^{n+1}$, where M is the maximum value of $\displaystyle ∣f^{(n+1)}(z)∣$ on the interval between a and the indicated point, yields $\displaystyle |R_n|≤\frac{1}{1000}$ on the indicated interval.

1. $\displaystyle f(x)=sinx$ on $\displaystyle [−π,π],a=0$

2. $\displaystyle f(x)=cosx$ on $\displaystyle [−\frac{π}{2},\frac{π}{2}],a=0$

Answer: Since $\displaystyle f^{(n+1)}(z)$ is $\displaystyle sinz$ or $\displaystyle cosz$, we have $\displaystyle M=1$. Since $\displaystyle |x−0|≤\frac{π}{2}$, we seek the smallest n such that $\displaystyle \frac{π^{n+1}}{2^{n+1}(n+1)!}≤0.001$. The smallest such value is $\displaystyle n=7$. The remainder estimate is $\displaystyle R_7≤0.00092.$

3. $\displaystyle f(x)=e^{−2x}$ on $\displaystyle [−1,1],a=0$

4. $\displaystyle f(x)=e^{−x}$ on $\displaystyle [−3,3],a=0$

Answer: Since $\displaystyle f^{(n+1)}(z)=±e^{−z}$ one has $\displaystyle M=e^3$. Since $\displaystyle |x−0|≤3$, one seeks the smallest n such that $\displaystyle \frac{3^{n+1}e^3}{(n+1)!}≤0.001$. The smallest such value is $\displaystyle n=14$. The remainder estimate is $\displaystyle R_{14}≤0.000220.$

Exercise $\PageIndex{5}$

In the following exercises, the maximum of the right-hand side of the remainder estimate $\displaystyle |R_1|≤\frac{max|f''(z)|}{2}R^2$ on $\displaystyle [a−R,a+R]$ occurs at a or $\displaystyle a±R$. Estimate the maximum value of R such that $\displaystyle \frac{max|f''(z)|}{2}R^2≤0.1$ on $\displaystyle [a−R,a+R]$ by plotting this maximum as a function of I.

1. $\displaystyle e^x$ approximated by $\displaystyle 1+x,a=0$

2. $\displaystyle sinx$ approximated by $\displaystyle x, a=0$

Answer

Since $\displaystyle sinx$ is increasing for small $\displaystyle x$ and since $\displaystyle sin''x=−sinx$, the estimate applies whenever $\displaystyle R^2sin(R)≤0.2$, which applies up to $\displaystyle R=0.596.$

$alt$

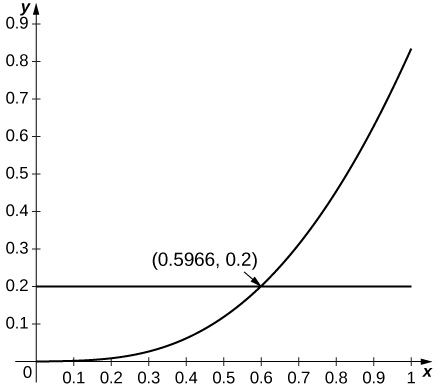
3. $\displaystyle lnx$ approximated by $\displaystyle x−1,a=1$

4. $\displaystyle cosx$ approximated by $\displaystyle 1,a=0$

Answer

Since the second derivative of $\displaystyle cosx$ is $\displaystyle −cosx$ and since $\displaystyle cosx$ is decreasing away from $\displaystyle x=0$, the estimate applies when $\displaystyle R^2cosR≤0.2$ or $\displaystyle R≤0.447$.

$alt$

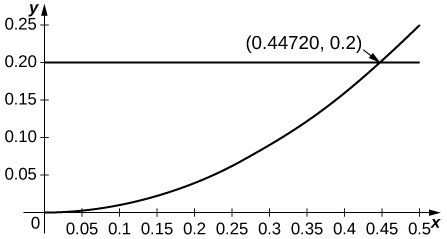
Exercise $\PageIndex{6}$

In the following exercises, find the Taylor series of the given function centered at the indicated point.

1. $\displaystyle x^4$ at $\displaystyle a=−1$

2. $\displaystyle 1+x+x^2+x^3$ at $\displaystyle a=−1$

Answer: $\displaystyle (x+1)^3−2(x+1)^2+2(x+1)$

3. $\displaystyle sinx$ at $\displaystyle a=π$

4. $\displaystyle cosx$ at $\displaystyle a=2π$

Answer: Values of derivatives are the same as for $\displaystyle x=0$ so $\displaystyle cosx=\sum_{n=0}^∞(−1)^n\frac{(x−2π)^{2n}}{(2n)!}$

5. $\displaystyle sinx$ at $\displaystyle x=\frac{π}{2}$

6. $\displaystyle cosx$ at $\displaystyle x=\frac{π}{2}$

Answer: $\displaystyle cos(\frac{π}{2})=0,−sin(\frac{π}{2})=−1$ so $\displaystyle cosx=\sum_{n=0}^∞(−1)^{n+1}\frac{(x−\frac{π}{2})^{2n+1}}{(2n+1)!}$, which is also $\displaystyle −cos(x−\frac{π}{2})$.

7. $\displaystyle e^x$ at $\displaystyle a=−1$

8. $\displaystyle e^x$ at $\displaystyle a=1$

Answer: The derivatives are $\displaystyle f^{(n)}(1)=e$ so $\displaystyle e^x=e\sum_{n=0}^∞\frac{(x−1)^n}{n!}.$

9. $\displaystyle \frac{1}{(x−1)^2}$ at $\displaystyle a=0$ (Hint: Differentiate $\displaystyle \frac{1}{1−x}$.)

10. $\displaystyle \frac{1}{(x−1)^3}$ at $\displaystyle a=0$

Answer: $\displaystyle \frac{1}{(x−1)^3}=−(\frac{1}{2})\frac{d^2}{dx^2}\frac{1}{1−x}=−\sum_{n=0}^∞(\frac{(n+2)(n+1)x^n}{2})$

11. $\displaystyle F(x)=∫^x_0cos(\sqrt{t})dt;f(t)=\sum_{n=0}^∞(−1)^n\frac{t^n}{(2n)!}$ at a=0 (Note: $\displaystyle f$ is the Taylor series of $\displaystyle cos(\sqrt{t}).)$

Exercise $\PageIndex{7}$

In the following exercises, compute the Taylor series of each function around $\displaystyle x=1$.

1. $\displaystyle f(x)=2−x$

Answer: $\displaystyle 2−x=1−(x−1)$

2. $\displaystyle f(x)=x^3$

3. $\displaystyle f(x)=(x−2)^2$

Answer: $\displaystyle ((x−1)−1)^2=(x−1)^2−2(x−1)+1$

4. $\displaystyle f(x)=lnx$

5. $\displaystyle f(x)=\frac{1}{x}$

Answer: $\displaystyle \frac{1}{1−(1−x)}=\sum_{n=0}^∞(−1)^n(x−1)^n$

6. $\displaystyle f(x)=\frac{1}{2x−x^2}$

7. $\displaystyle f(x)=\frac{x}{4x−2x^2−1}$

Answer: $\displaystyle x\sum_{n=0}^∞2^n(1−x)^{2n}=\sum_{n=0}^∞2^n(x−1)^{2n+1}+\sum_{n=0}^∞2^n(x−1)^{2n}$

8. $\displaystyle f(x)=e^{−x}$

9. $\displaystyle f(x)=e^{2x}$

Answer: $\displaystyle e^{2x}=e^{2(x−1)+2}=e^2\sum_{n=0}^∞\frac{2^n(x−1)^n}{n!}$

Exercise $\PageIndex{8}$

In the following exercises, identify the value of x such that the given series $\displaystyle \sum_{n=0}^∞a_n$ is the value of the Maclaurin series of $\displaystyle f(x)$ at $\displaystyle x$. Approximate the value of $\displaystyle f(x)$ using $\displaystyle S_{10}=\sum_{n=0}^{10}a_n$.

1. $\displaystyle \sum_{n=0}^∞\frac{1}{n!}$

2. $\displaystyle sum_{n=0}^∞\frac{2^n}{n!}$

Answer: $\displaystyle x=e^2;S_{10}=\frac{34,913}{4725}≈7.3889947$

3. $\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n}}{(2n)!}$

4. $\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n+1}}{(2n+1)!}$

Answer: $\displaystyle sin(2π)=0;S_{10}=8.27×10^{−5}$

Exercise $\PageIndex{9}$

The following exercises make use of the functions $\displaystyle S_5(x)=x−\frac{x^3}{6}+\frac{x^5}{120}$ and $\displaystyle C_4(x)=1−\frac{x^2}{2}+\frac{x^4}{24}$ on $\displaystyle [−π,π]$.

1. Plot $\displaystyle sin^2x−(S_5(x))^2$ on $\displaystyle [−π,π]$. Compare the maximum difference with the square of the Taylor remainder estimate for $\displaystyle sinx.$

2. Plot $\displaystyle cos^2x−(C_4(x))^2$ on $\displaystyle [−π,π]$. Compare the maximum difference with the square of the Taylor remainder estimate for $\displaystyle cosx$.

Answer

The difference is small on the interior of the interval but approaches $\displaystyle 1$ near the endpoints. The remainder estimate is $\displaystyle |R_4|=\frac{π^5}{120}≈2.552.$

$alt$

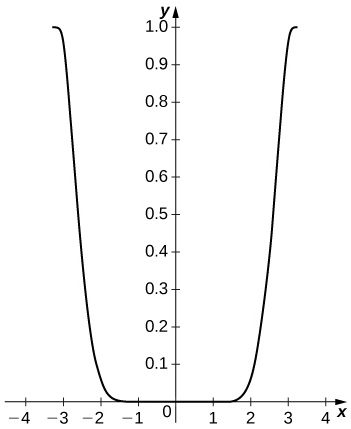
3. Plot $\displaystyle |2S_5(x)C_4(x)−sin(2x)|$ on $\displaystyle [−π,π]$.

4. Compare $\displaystyle \frac{S_5(x)}{C_4(x)}$ on $\displaystyle [−1,1]$ to $\displaystyle tanx$. Compare this with the Taylor remainder estimate for the approximation of $\displaystyle tanx$ by $\displaystyle x+\frac{x^3}{3}+\frac{2x^5}{15}$.

Answer

The difference is on the order of $\displaystyle 10^{−4}$ on $\displaystyle [−1,1]$ while the Taylor approximation error is around $\displaystyle 0.1$ near $\displaystyle ±1$. The top curve is a plot of $\displaystyle tan^2x−(\frac{S_5(x)}{C_4(x)})^2$ and the lower dashed plot shows $\displaystyle t^2−(\frac{S_5}{C_4})^2$.

$alt$

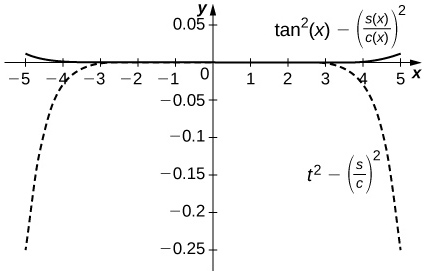
5. Plot $\displaystyle e^x−e_4(x)$ where $\displaystyle e_4(x)=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}$ on $\displaystyle [0,2]$. Compare the maximum error with the Taylor remainder estimate.

Exercise $\PageIndex{10}$

1. (Taylor approximations and root finding.) Recall that Newton’s method $\displaystyle x_{n+1}=x_n−\frac{f(x_n)}{f'(x_n)}$ approximates solutions of $\displaystyle f(x)=0$ near the input $\displaystyle x_0$.

a. If $\displaystyle f$ and $\displaystyle g$ are inverse functions, explain why a solution of $\displaystyle g(x)=a$ is the value $\displaystyle f(a)$ of $\displaystyle f$.

b. Let $\displaystyle p_N(x)$ be the $\displaystyle Nth$ degree Maclaurin polynomial of $\displaystyle e^x$. Use Newton’s method to approximate solutions of $\displaystyle p_N(x)−2=0$ for $\displaystyle N=4,5,6.$

c. Explain why the approximate roots of $\displaystyle p_N(x)−2=0$ are approximate values of $\displaystyle ln(2).$

Answer

a. Answers will vary.

b. The following are the $\displaystyle x_n$ values after $\displaystyle 10$ iterations of Newton’s method to approximation a root of $\displaystyle p_N(x)−2=0$: for $\displaystyle N=4,x=0.6939...;$ for $\displaystyle N=5,x=0.6932...;$ for $\displaystyle N=6,x=0.69315...;.$ (Note: $\displaystyle ln(2)=0.69314...$)

c. Answers will vary.

Exercise $\PageIndex{11}$

In the following exercises, use the fact that if $\displaystyle q(x)=\sum_{n=1}^∞a_n(x−c)^n$ converges in an interval containing $\displaystyle c$, then $\displaystyle \lim_{x→c}q(x)=a_0$ to evaluate each limit using Taylor series.

1. $\displaystyle \lim_{x→0}\frac{cosx−1}{x^2}$

2. $\displaystyle \lim_{x→0}\frac{ln(1−x^2)}{x^2}$

Answer: $\displaystyle \frac{ln(1−x^2)}{x^2}→−1$

3. $\displaystyle \lim_{x→0}\frac{e^{x^2}−x^2−1}{x^4}$

4. $\displaystyle \lim_{x→0^+}\frac{cos(\sqrt{x})−1}{2x}$

Answer: $\displaystyle \frac{cos(\sqrt{x})−1}{2x}≈\frac{(1−\frac{x}{2}+\frac{x^2}{4!}−⋯)−1}{2x}→−\frac{1}{4}$

Search

Text Color

Text Size

Margin Size

Font Type

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)