4.6: Constant Coefficient Homogeneous Systems III
- Page ID
- 17439
This page is a draft and is under active development.
Constant Coefficient Homogeneous Systems III
We now consider the system \({\bf y}'=A{\bf y}\), where \(A\) has a complex eigenvalue \(\lambda = \alpha + i\beta\) with \(\beta\ne0\). We continue to assume that \(A\) has real entries, so the characteristic polynomial of \(A\) has real coefficients. This implies that \(overline\lambda = \alpha - i\beta\) is also an eigenvalue of \(A\).
An eigenvector \({\bf x}\) of \(A\) associated with \(\lambda = \alpha + i\beta\) will have complex entries, so we'll write
\begin{eqnarray*}
{\bf x} = {\bf u} + i{\bf v}
\end{eqnarray*}
where \({\bf u}\) and \({\bf v}\) have real entries; that is, \({\bf u}\) and \({\bf v}\) are the real and imaginary parts of \({\bf x}\). Since \(A{\bf x} = \lambda {\bf x}\),
\begin{equation} \label{eq:4.6.1}
A({\bf u}+i{\bf v})=(\alpha+i\beta)({\bf u}+i{\bf v}).
\end{equation}
Taking complex conjugates here and recalling that \(A\) has real entries yields
\begin{eqnarray*}
A ({\bf u} - i{\bf v}) = (\alpha - i\beta) ({\bf u} - i{\bf v}),
\end{eqnarray*}
which shows that \({\bf x}={\bf u}-i{\bf v}\) is an eigenvector associated with \(\overline\lambda=\alpha-i\beta\). The complex conjugate eigenvalues \(\lambda\) and \(\overline\lambda\) can be separately associated with linearly independent solutions \({\bf y}'=A{\bf y}\); however, we won't pursue this approach, since solutions obtained in this way turn out to be complex-valued. Instead, we'll obtain solutions of \({\bf y}'=A{\bf y}\) in the form
\begin{equation} \label{eq:4.6.2}
{\bf y}=f_1{\bf u}+f_2{\bf v}
\end{equation}
where \(f_1\) and \(f_2\) are real-valued scalar functions. The next theorem shows how to do this.
Theorem \(\PageIndex{1}\)
Let \(A\) be an \(n\times n\) matrix with real entries. Let \(\lambda=\alpha+i\beta\) \(\beta\ne0\) be a complex eigenvalue of \(A\) and let \({\bf x}={\bf u}+i{\bf v}\) be an associated eigenvector, where \({\bf u}\) and \({\bf v}\) have real components. Then
\({\bf u}\) and \({\bf v}\) are both nonzero and
\begin{eqnarray*}
{\bf y}_1 = e^{\alpha t} ({\bf u} \cos \beta t - {\bf v} \sin \beta t) \quad \mbox{and} \quad {\bf y}_2 = e^{\alpha t}({\bf u} \sin \beta t + {\bf v} \cos \beta t),
\end{eqnarray*}
which are the real and imaginary parts of
\begin{equation} \label{eq:4.6.3}
e^{\alpha t}(\cos\beta t+i\sin\beta t)({\bf u}+i{\bf v}),
\end{equation}
are linearly independent solutions of \({\bf y}'=A{\bf y}\).
- Proof
-
A function of the form \eqref{eq:4.6.2} is a solution of \({\bf y}'=A{\bf y}\) if and only if
\begin{equation} \label{eq:4.6.4}
f_1'{\bf u}+f_2'{\bf
v}=f_1A{\bf u}+f_2A{\bf v}.
\end{equation}Carrying out the multiplication indicated on the right side of \eqref{eq:4.6.1} and collecting the real and imaginary parts of the result yields
\begin{eqnarray*}
A ({\bf u} + i{\bf v}) = (\alpha {\bf u} - \beta {\bf v}) + i(\alpha {\bf v} + \beta {\bf u}).
\end{eqnarray*}Equating real and imaginary parts on the two sides of this equation yields
\begin{eqnarray*}
\begin{array} \\ A {\bf u} &=& \alpha {\bf u} - \beta {\bf v} \\ A {\bf v} &=& \alpha {\bf v} + \beta {\bf u} \end{array}.
\end{eqnarray*}We leave it to you (Exercise \((4.6E.25)\)) to show from this that \({\bf u}\) and \({\bf v}\) are both nonzero. Substituting from these equations into \eqref{eq:4.6.4} yields
\begin{eqnarray*}
f_1'{\bf u}+f_2'{\bf v}
&=&f_1(\alpha{\bf u}-\beta{\bf v})+f_2(\alpha{\bf v}+\beta{\bf u})\\
&=&(\alpha f_1+\beta f_2){\bf u}+(-\beta f_1+\alpha f_2){\bf v}.
\end{eqnarray*}This is true if
\begin{eqnarray*}
\begin{array} \\ f_1' &=& \alpha f_1 + \beta f_2 \phantom{,} \\ f_2' &=& -\beta f_1 + \alpha f_2, \end{array} \quad \mbox{or, equivalently,} \quad \begin{array} f_1' -\alpha f_1 &=& \phantom{-} \beta f_2 \phantom{.} \\ f_2' - \alpha f_2 &=& -\beta f_1. \end{array}
\end{eqnarray*}If we let \(f_1=g_1e^{\alpha t}\) and \(f_2=g_2e^{\alpha t}\), where \(g_1\) and \(g_2\) are to be determined, then the last two equations become
\begin{eqnarray*}
\begin{array} \\ g_1' &=& \beta g_2 \phantom{.} \\ g_2' &=& -\beta g_1, \end{array}
\end{eqnarray*}which implies that
\begin{eqnarray*}
g_1'' = \beta g_2' = -\beta^2 g_1,
\end{eqnarray*}so
\begin{eqnarray*}
g_1'' + \beta^2 g_1 = 0
\end{eqnarray*}The general solution of this equation is
\begin{eqnarray*}
g_1 = c_1 \cos \beta t + c_2 \sin \beta t.
\end{eqnarray*}Moreover, since \(g_2=g_1'/\beta\),
\begin{eqnarray*}
g_2 = -c_1 \sin \beta t + c_2 \cos \beta t.
\end{eqnarray*}Multiplying \(g_1\) and \(g_2\) by \(e^{\alpha t}\) shows that
\begin{eqnarray*}
f_1&=&e^{\alpha t}(\phantom{-}c_1\cos\beta t+c_2\sin\beta t ),\\
f_2&=&e^{\alpha t}(-c_1\sin\beta t+c_2\cos\beta t).
\end{eqnarray*}Substituting these into \eqref{eq:4.6.2} shows that
\begin{equation} \label{eq:4.6.5}
\begin{array}{rcl}
{\bf y}&=&e^{\alpha t}\left[(c_1\cos\beta t+c_2\sin\beta t){\bf u}
+(-c_1\sin\beta t+c_2\cos\beta t){\bf v}\right]\\
&=&c_1e^{\alpha t}({\bf u}\cos\beta t-{\bf v}\sin\beta t)
+c_2e^{\alpha t}({\bf u}\sin\beta t+{\bf v}\cos\beta t)
\end{array}
\end{equation}is a solution of \({\bf y}'=A{\bf y}\) for any choice of the constants \(c_1\) and \(c_2\). In particular, by first taking \(c_1=1\) and \(c_2=0\) and then taking \(c_1=0\) and \(c_2=1\), we see that \({\bf y}_1\) and \({\bf y}_2\) are solutions of \( {\bf y}'=A{\bf y}\). We leave it to you to verify that they are, respectively, the real and imaginary parts of \eqref{eq:4.6.3} (Exercise \((4.6E.26)\)), and that they are linearly independent (Exercise \((4.6E.27)\)).
Example \(\PageIndex{1}\)
Find the general solution of
\begin{equation} \label{eq:4.6.6}
{\bf y}' = \left[ \begin{array} \\ 4 & {-5} \\ 5 & {-2} \end{array} \right] \bf y.
\end{equation}
- Answer
-
The characteristic polynomial of the coefficient matrix \(A\) in \eqref{eq:4.6.6} is
\begin{eqnarray*}
\left| \begin{array} \\ 4 -\lambda & -5 \\ 5 & -2 - \lambda \end{array} \right| = (\lambda -1)^2 + 16.
\end{eqnarray*}Hence, \(\lambda=1+4i\) is an eigenvalue of \(A\). The associated eigenvectors satisfy \(\left(A-\left(1+4i\right)I\right){\bf x}={\bf 0}\). The augmented matrix of this system is
\begin{eqnarray*}
\left[ \begin{array} \\ 3-4i & -5 & \vdots & 0 \\ 5 & -3-4i & \vdots & 0 \end{array} \right],
\end{eqnarray*}which is row equivalent to
\begin{eqnarray*}
\left[ \begin{array} \\ 1 & -{3+4i \over 5} & \vdots & 0 \\ 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}Therefore \(x_1=(3+4i)x_2/5\). Taking \(x_2=5\) yields \(x_1=3+4i\), so
\begin{eqnarray*}
{\bf x} = \left[ \begin{array} \\ 3+4i \\ 5 \end{array} \right]
\end{eqnarray*}is an eigenvector. The real and imaginary parts of
\begin{eqnarray*}
e^t (\cos 4t + i \sin 4t) \left[ \begin{array} \\ 3+4i \\ 5 \end{array} \right]
\end{eqnarray*}are
\begin{eqnarray*}
{\bf y}_1 = e^t \left[ \begin{array} \\ 3 \cos 4t-4 \sin 4t \\ 5 \cos 4t \end{array} \right] \quad \mbox{and} \quad {\bf y}_2 = e^t \left[ \begin{array} \\ 3 \sin 4t + 4 \cos 4t \\ 5 \sin 4t \end{array} \right],
\end{eqnarray*}which are linearly independent solutions of \eqref{eq:4.6.6}. The general solution of \eqref{eq:4.6.6} is
\begin{eqnarray*}
{\bf y} = c_1 e^t \left[ \begin{array} \\ 3 \cos 4t-4 \sin 4t \\ 5 \cos 4t \end{array} \right] + c_2 e^t \left[ \begin{array} \\ 3 \sin 4t+4 \cos 4t \\ 5 \sin 4t \end{array} \right].
\end{eqnarray*}
Example \(\PageIndex{2}\)
Find the general solution of
\begin{equation} \label{eq:4.6.7}
{\bf y}' = \left[ \begin{array} \\ {-14} & {39} \\ {-6} & {16} \end{array} \right]{\bf y}.
\end{equation}
- Answer
-
The characteristic polynomial of the coefficient matrix \(A\) in \eqref{eq:4.6.7} is
\begin{eqnarray*}
\left| \begin{array} \\ -14 - \lambda & 39 \\ -6 & 16 - \lambda \end{array} \right| = (\lambda - 1)^2 + 9.
\end{eqnarray*}Hence, \(\lambda=1+3i\) is an eigenvalue of \(A\). The associated eigenvectors satisfy \(\left(A-(1+3i)I\right){\bf x}={\bf 0}\). The augmented augmented matrix of this system is
\begin{eqnarray*}
\left[ \begin{array} \\ -15-3i & 39 & \vdots & 0 \\ -6 & 15-3i & \vdots & 0 \end{array} \right],
\end{eqnarray*}which is row equivalent to
\begin{eqnarray*}
\left[ \begin{array} \\ 1 & {-5+i \over 2} & \vdots & 0 \\ 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}Therefore \(x_1=(5-i)/2\). Taking \(x_2=2\) yields \(x_1=5-i\), so
\begin{eqnarray*}
{\bf x} = \left[ \begin{array} \\ 5-i \\ 2 \end{array} \right]
\end{eqnarray*}is an eigenvector. The real and imaginary parts of
\begin{eqnarray*}
e^t (\cos 3t + i \sin 3t) \left[ \begin{array} \\ 5-i \\ 2 \end{array} \right]
\end{eqnarray*}are
\begin{eqnarray*}
{\bf y}_1 = e^t \left[ \begin{array} \\ \sin 3t + 5 \cos 3t \\ 2 \cos 3t \end{array} \right] \quad \mbox{and} \quad {\bf y}_2 = e^t \left[ \begin{array} \\ -\cos 3t + 5 \sin 3t \\ 2 \sin 3t \end{array} \right],
\end{eqnarray*}which are linearly independent solutions of \eqref{eq:4.6.7}. The general solution of \eqref{eq:4.6.7} is
\begin{eqnarray*}
{\bf y} = c_1 e^t \left[ \begin{array} \\ \sin 3t + 5 \cos 3t \\ 2 \cos 3t \end{array} \right] + c_2 e^t \left[ \begin{array} \\ -\cos 3t + 5 \sin 3t \\ 2 \sin 3t \end{array} \right].
\end{eqnarray*}
Example \(\PageIndex{3}\)
Find the general solution of
\begin{equation} \label{eq:4.6.8}
{\bf y}' = \left[ \begin{array} \\ {-5} & 5 & 4 \\ {-8} & 7 & 6 \\ 1 & 0 & 0 \end{array} \right] {\bf y}.
\end{equation}
- Answer
-
The characteristic polynomial of the coefficient matrix \(A\) in \eqref{eq:4.6.8} is
\begin{eqnarray*}
\left| \begin{array} \\ -5 - \lambda & 5 & 4 \\ -8 & 7 - \lambda & 6 \\ \phantom{-} 1 & 0 & -\lambda \end{array} \right| = -(\lambda-2)(\lambda^2 + 1).
\end{eqnarray*}Hence, the eigenvalues of \(A\) are \(\lambda_1=2\), \(\lambda_2=i\), and \(\lambda_3=-i\). The augmented matrix of \((A-2I){\bf x=0}\) is
\begin{eqnarray*}
\left[ \begin{array} \\ -7 & 5 & 4 & \vdots & 0 \\ -8 & 5 & 6 & \vdots & 0 \\ 1 & 0 & -2 & \vdots & 0 \end{array} \right],
\end{eqnarray*}which is row equivalent to
\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 0 & -2 & \vdots & 0 \\ 0 & 1 & -2 & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}Therefore \(x_1=x_2=2x_3\). Taking \(x_3=1\) yields
\begin{eqnarray*}
{\bf x}_1 = \left[ \begin{array} \\ 2 \\ 2 \\ 1 \end{array} \right],
\end{eqnarray*}so
\begin{eqnarray*}
{\bf y}_1 = \left[ \begin{array} \\ 2 \\ 2 \\ 1 e^{2t} \end{array} \right]
\end{eqnarray*}is a solution of \eqref{eq:4.6.8}.
The augmented matrix of \((A-iI){\bf x=0}\) is
\begin{eqnarray*}
\left[ \begin{array} \\ -5-i & 5 & 4 & \vdots & 0 \\ -8 & 7-i & 6 & \vdots & 0 \\ \phantom{-} 1 & 0 & -i & \vdots & 0 \end{array} \right],
\end{eqnarray*}which is row equivalent to
\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 0 & -i & \vdots & 0 \\ 0 & 1 & 1-i & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}Therefore \(x_1=ix_3\) and \(x_2=-(1-i)x_3\). Taking \(x_3=1\) yields the eigenvector
\begin{eqnarray*}
{\bf x}_2 = \left[ \begin{array} \\ i \\ -1+i \\ 1 \end{array} \right].
\end{eqnarray*}The real and imaginary parts of
\begin{eqnarray*}
(\cos t+i \sin t) \left[ \begin{array} \\ i \\ -1+i \\ 1 \end{array} \right]
\end{eqnarray*}are
\begin{eqnarray*}
{\bf y}_2 = \left[ \begin{array} \\ -\sin t \\ -\cos t - \sin t \\ \cos t \end{array} \right] \quad \mbox{and} \quad {\bf y}_3 = \left[ \begin{array} \\ \cos t \\ \cos t - \sin t \\ \sin t \end{array} \right],
\end{eqnarray*}which are solutions of \eqref{eq:4.6.8}. Since the Wronskian of \(\{{\bf y}_1,{\bf y}_2,{\bf y}_3\}\) at \(t=0\) is
\begin{eqnarray*}
\left| \begin{array} \\ 2 & 0 & 1 \\ 2 & -1 & 1 \\ 1 & 1 & 0 \end{array} \right| = 1,
\end{eqnarray*}\(\{{\bf y}_1,{\bf y}_2,{\bf y}_3\}\) is a fundamental set of solutions of \eqref{eq:4.6.8}. The general solution of \eqref{eq:4.6.8} is
\begin{eqnarray*}
{\bf y} = c_1 \left[ \begin{array} \\ 2 \\ 2 \\ 1 e^{2t} \end{array} \right] + c_2 \left[ \begin{array} \\ -\sin t \\ -\cos t -\sin t \\ \cos t \end{array} \right] + c_3 \left[ \begin{array} \\ \cos t \\ \cos t - \sin t \\ \sin t \end{array} \right].
\end{eqnarray*}
Example\(\PageIndex{4}\)
Find the general solution of
\begin{equation} \label{eq:4.6.9}
{\bf y}' = \left[ \begin{array} \\ 1 & {-1} & {-2} \\ 1 & 3 & 2 \\ 1 & {-1} & 2 \end{array} \right] {\bf y}.
\end{equation}
- Answer
-
The characteristic polynomial of the coefficient matrix \(A\) in \eqref{eq:4.6.9} is
\begin{eqnarray*}
\left| \begin{array} \\ 1 - \lambda & -1 & -2 \\ 1 & 3-\lambda & \phantom{-} 2 \\ 1 & -1 & 2-\lambda \end{array} \right| = -(\lambda - 2) \left( (\lambda-2)^2 + 4 \right).
\end{eqnarray*}Hence, the eigenvalues of \(A\) are \(\lambda_1=2\), \(\lambda_2=2+2i\), and \(\lambda_3=2-2i\). The augmented matrix of \((A-2I){\bf x=0}\) is
\begin{eqnarray*}
\left[ \begin{array} \\ -1 & -1 & -2 & \vdots & 0 \\ 1 & 1 & 2 & \vdots & 0 \\ 1 & -1 & 0 & \vdots & 0 \end{array} \right],
\end{eqnarray*}which is row equivalent to
\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 0 & 1 & \vdots & 0 \\ 0 & 1 & 1 & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}Therefore \(x_1=x_2=-x_3\). Taking \(x_3=1\) yields
\begin{eqnarray*}
{\bf x}_1 = \left[ \begin{array} \\ -1 \\ -1 \\ 1 \end{array} \right],
\end{eqnarray*}so
\begin{eqnarray*}
{\bf y}_1 = \left[ \begin{array} \\ -1 \\ -1 \\ 1 e^{2t} \end{array} \right]
\end{eqnarray*}is a solution of \eqref{eq:4.6.9}.
The augmented matrix of \(\left(A-(2+2i)I\right){\bf x=0}\) is
\begin{eqnarray*}
\left[ \begin{array} \\ -1-2i & -1 & -2 & \vdots & 0 \\ 1 & 1-2i & \phantom{-} 2 & \vdots & 0 \\ 1 & -1 & -2 & \vdots & 0 \end{array} \right],
\end{eqnarray*}which is row equivalent to
\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 0 & -i & \vdots & 0 \\ 0 & 1 & i & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}Therefore \(x_1=ix_3\) and \(x_2=-ix_3\). Taking \(x_3=1\) yields the eigenvector
\begin{eqnarray*}
{\bf x}_2 = \left[ \begin{array} \\ i \\ -i \\ 1 \end{array} \right]
\end{eqnarray*}The real and imaginary parts of
\begin{eqnarray*}
e^{2t} (\cos 2t + i \sin 2t) \left[ \begin{array} \\ i \\ -i \\ 1 \end{array} \right]
\end{eqnarray*}are
\begin{eqnarray*}
{\bf y} _2 = e^{2t} \left[ \begin{array} \\ -\sin 2t \\ \sin 2t \\ \cos 2t \end{array} \right] \quad \mbox{and} \quad {\bf y}_2 = e^{2t} \left[ \begin{array} \\ \cos 2t \\ -\cos 2t \\ \sin 2t \end{array} \right],
\end{eqnarray*}which are solutions of \eqref{eq:4.6.9}. Since the Wronskian of \(\{{\bf y}_1,{\bf y}_2,{\bf y}_3\}\) at \(t=0\) is
\begin{eqnarray*}
\left| \begin{array} \\ -1 & 0 & 1 \\ -1 & 0 & -1 \\ 1 & 1 & 0 \end{array} \right| = -2,
\end{eqnarray*}\(\{{\bf y}_1,{\bf y}_2,{\bf y}_3\}\) is a fundamental set of solutions of \eqref{eq:4.6.9}. The general solution of \eqref{eq:4.6.9} is
\begin{eqnarray*}
{\bf y} = c_1 \left[ \begin{array} \\ -1 \\ -1 \\ 1 e^{2t} \end{array} \right] + c_2 e^{2t} \left[ \begin{array} \\ -\sin 2t \\ \sin 2t \\ \cos 2t \end{array} \right] + c_3 e^{2t} \left[ \begin{array} \\ \cos 2t \\ -\cos 2t \\ \sin 2t \end{array} \right].
\end{eqnarray*}
Geometric Properties of Solutions when \(n=2\)
We'll now consider the geometric properties of solutions of a \(2\times2\) constant coefficient system
\begin{equation} \label{eq:4.6.10}
\left[ \begin{array} \\ {y_1'} \\ {y_2'} \end{array} \right] = \left[\begin{array}{cc}a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] \left[ \begin{array} \\ {y_1} \\ {y_2} \end{array} \right]
\end{equation}
under the assumptions of this section; that is, when the matrix
\begin{eqnarray*}
A = \left[ \begin{array} \\ a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]
\end{eqnarray*}
has a complex eigenvalue \(\lambda = \alpha + i\beta\) \(\beta\ne0\){\rm}) and \({\bf x}={\bf u}+i{\bf v}\) is an associated eigenvector, where \({\bf u}\) and \({\bf v}\) have real components. To describe the trajectories accurately it's necessary to introduce a new rectangular coordinate system in the \(y_1\)-\(y_2\) plane. This raises a point that hasn't come up before: It is always possible to choose \({\bf x}\) so that \(({\bf u},{\bf v})=0\). A special effort is required to do this, since not every eigenvector has this property. However, if we know an eigenvector that doesn't, we can multiply it by a suitable complex constant to obtain one that does. To see this, note that if \({\bf x}\) is a \(\lambda\)-eigenvector of \(A\) and \(k\) is an arbitrary real number, then
\begin{eqnarray*}
{\bf x}_1 = (1+ik){\bf x} = (1 + ik) ({\bf u} + i{\bf v}) = ({\bf u} - k{\bf v}) + i({\bf v} + k{\bf u})
\end{eqnarray*}
is also a \(\lambda\)-eigenvector of \(A\), since
\begin{eqnarray*}
A {\bf x}_1 = A ((1 + ik){\bf x}) = (1 + ik) A {\bf x} = (1 + ik) \lambda {\bf x} = \lambda ((1 + ik){\bf x}) = \lambda{\bf x}_1.
\end{eqnarray*}
The real and imaginary parts of \({\bf x}_1\) are
\begin{equation} \label{eq:4.6.11}
{\bf u}_1={\bf u}-k{\bf v} \quad \mbox{ and } \quad {\bf v}_1={\bf v}+k{\bf u},
\end{equation}
so
\begin{eqnarray*}
({\bf u}_1, {\bf v}_1) = ({\bf u} - k{\bf v}, {\bf v} + k{\bf u}) = -\left[ ({\bf u}, {\bf v}) k^2 + (\|{\bf v}\|^2 - \|{\bf u}\|^2 k - ({\bf u},{\bf v})\right].
\end{eqnarray*}
Therefore \(({\bf u}_1,{\bf v}_1)=0\) if
\begin{equation} \label{eq:4.6.12}
({\bf u},{\bf v})k^2+(\|{\bf v}\|^2-\|{\bf u}\|^2)k-({\bf u},{\bf v})=0.
\end{equation}
If \(({\bf u},{\bf v})\ne0\) we can use the quadratic formula to find two real values of \(k\) such that \(({\bf u}_1,{\bf v}_1)=0\) (Exercise \((4.6E.28)\)).
Example \(\PageIndex{5}\):
In Example \((4.6.1)\), we found the eigenvector
\begin{eqnarray*}
{\bf x} - \left[ \begin{array} \\ 3+4i \\ 5 \end{array} \right] = \left[ \begin{array} \\ 3 \\ 5 \end{array} \right] + i \left[ \begin{array} \\ 4 \\ 0 \end{array} \right]
\end{eqnarray*}
for the matrix of the system \eqref{eq:4.6.6}. Here \({\bf u}=\displaystyle { \left[ \begin{array} \\ 3 \\ 5 \end{array} \right] }\) and \({\bf v} = \left[ \begin{array} \\ 4 \\ 0 \end{array} \right] \) are not orthogonal, since \(({\bf u},{\bf v})=12\). Since \(\|{\bf v}\|^2-\|{\bf u}\|^2=-18\), \eqref{eq:4.6.12} is equivalent to
\begin{eqnarray*}
2k^2 -3k -1 = 0.
\end{eqnarray*}
The zeros of this equation are \(k_1=2\) and \(k_2=-1/2\). Letting \(k=2\) in \eqref{eq:4.6.11} yields
\begin{eqnarray*}
{\bf u}_1 = {\bf u}-2{\bf v} = \left[ \begin{array} \\ -5 \\ \phantom{-} 5 \end{array} \right] \quad \mbox{and} \quad {\bf v}_1 = {\bf v} + 2 {\bf u} = \left[ \begin{array} \\ 10 \\ 10 \end{array} \right],
\end{eqnarray*}
and \(({\bf u}_1,{\bf v}_1)=0\). Letting \(k=-1/2\) in \eqref{eq:4.6.11} yields
\begin{eqnarray*}
{\bf u}_1 = {\bf u} + {{\bf v} \over 2} = \left[ \begin{array} \\ 5 \\ 5 \end{array} \right] \quad \mbox{and} \quad {\bf v}_1 = {\bf v} - {{\bf u} \over 2} = {1 \over 2} \left[ \begin{array} \\ -5 \\ \phantom{-} 5 \end{array} \right],
\end{eqnarray*}
and again \(({\bf u}_1,{\bf v}_1)=0\).
(The numbers don't always work out as nicely as in this example. You'll need a calculator or computer to do Exercises \((4.6E.29)\) to \((4.6E.40)\).)
Henceforth, we'll assume that \(({\bf u},{\bf v})=0\). Let \({\bf U}\) and \({\bf V}\) be unit vectors in the directions of \({\bf u}\) and \({\bf v}\), respectively; that is, \({\bf U}={\bf u}/\|{\bf u}\|\) and \({\bf V}={\bf v}/\|{\bf v}\|\). The new rectangular coordinate system will
have the same origin as the \(y_1\)-\(y_2\) system. The coordinates of a point in this system will be denoted by \((z_1,z_2)\), where \(z_1\) and \(z_2\) are the displacements in the directions of \({\bf U}\) and \({\bf V}\), respectively.
From \eqref{eq:4.6.5}, the solutions of \eqref{eq:4.6.10} are given by
\begin{equation} \label{eq:4.6.13} {\bf y}=e^{\alpha t}\left[(c_1\cos\beta
t+c_2\sin\beta t){\bf u} +(-c_1\sin\beta t+c_2\cos\beta t){\bf
v}\right]. \end{equation}
For convenience, let's call the curve traversed by \(e^{-\alpha t}{\bf y}(t)\) a \( \textcolor{blue}{\mbox{shadow trajectory}} \) of \eqref{eq:4.6.10}. Multiplying \eqref{eq:4.6.13} by \(e^{-\alpha t}\) yields
\begin{eqnarray*}
e^{-\alpha t} {\bf y} (t) = z_1(t) {\bf U} + z_2 (t) {\bf V},
\end{eqnarray*}
where
\begin{eqnarray*}
z_1(t)&=&\|{\bf u}\|(c_1\cos\beta t+c_2\sin\beta
t)\\ z_2(t)&=&\|{\bf v}\|(-c_1\sin\beta t+c_2\cos\beta t).
\end{eqnarray*}
Therefore
\begin{eqnarray*}
{(z_1(t))^2 \over \| {\bf u} \|^2} + {(z_2(t))^2 \over \| {\bf v} \|^2} = c_1^2 + c_2^2
\end{eqnarray*}
(verify!), which means that the shadow trajectories of \eqref{eq:4.6.10} are ellipses centered at the origin, with axes of symmetry parallel to \({\bf U}\) and \({\bf V}\). Since
\begin{eqnarray*}
z_1' = {\beta \| {\bf u} \| \over \| {\bf v} \|} z_2 \quad \mbox{and} \quad z_2' = -{\beta \| {\bf v} \| \over \| {\bf u} \|} z_1,
\end{eqnarray*}
the vector from the origin to a point on the shadow ellipse rotates in the same direction that \({\bf V}\) would have to be rotated by \(\pi/2\) radians to bring it into coincidence with \({\bf U}\) (Figures \(4.6.1\) and \(4.6.2\)).
Figure \(4.6.1\)
Shadow trajectories traversed clockwise
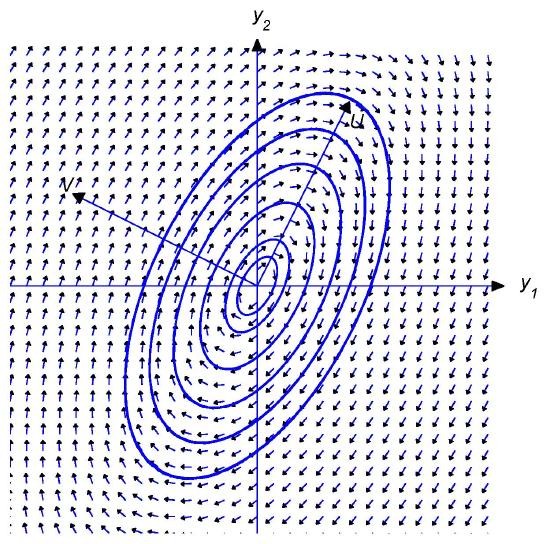
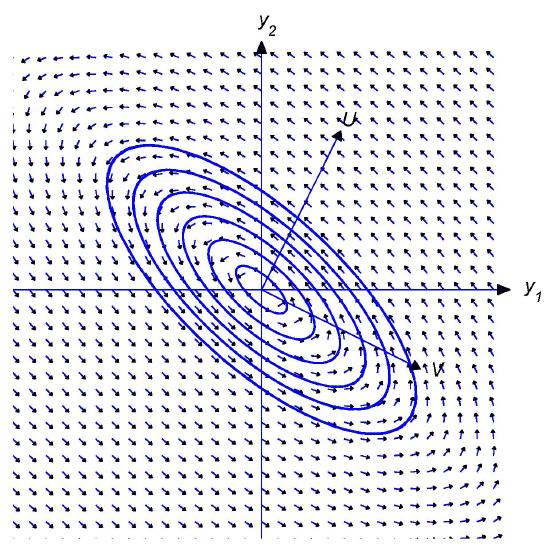
Figure \(4.6.2\)
Shadow trajectories traversed counterclockwise
If \(\alpha>0\), then
\begin{eqnarray*}
\lim_{t\to\infty} \| {\bf y}(t) \| = \infty \quad \mbox{and} \quad \lim_{t\to-\infty} {\bf y}(t) = 0,
\end{eqnarray*}
so the trajectory spirals away from the origin as \(t\) varies from \(-\infty\) to \(\infty\). The direction of the spiral depends upon the relative orientation of \({\bf U}\) and \({\bf V}\), as shown in Figures \(4.6.3\) and \(4.6.4\).
If \(\alpha<0\), then
\begin{eqnarray*}
\lim_{t\to-\infty} \| {\bf y}(t) \| = \infty \quad \mbox{and} \quad \lim_{t\to\infty}{\bf y}(t) = 0,
\end{eqnarray*}
so the trajectory spirals toward the origin as \(t\) varies from \(-\infty\) to \(\infty\). Again, the direction of the spiral depends upon the relative orientation of \({\bf U}\) and \({\bf V}\), as shown in Figures \(4.6.5\) and \(4.6.6\).
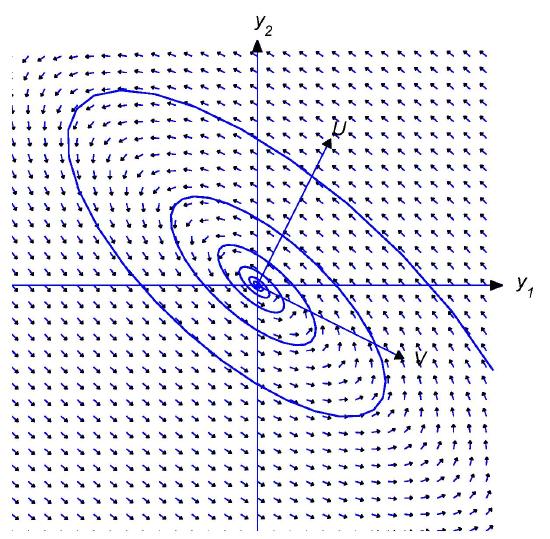
Figure \(4.6.3\)
\(\alpha>0\); shadow trajectory spiraling outward
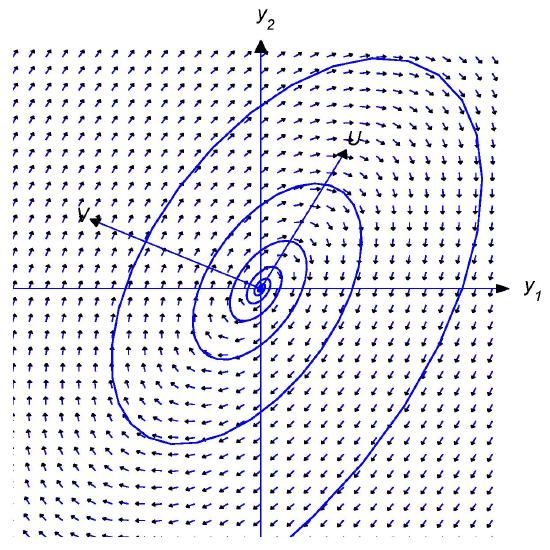
Figure \(4.6.4\)
\(\alpha>0\); shadow trajectory spiraling outward
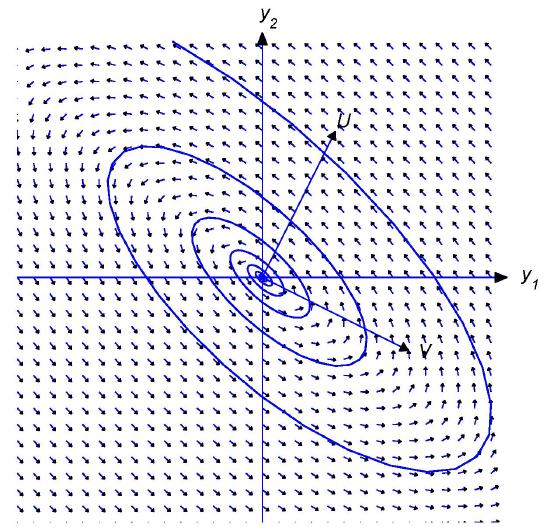
Figure \(4.6.5\)
\(\alpha<0\); shadow trajectory spiraling inward
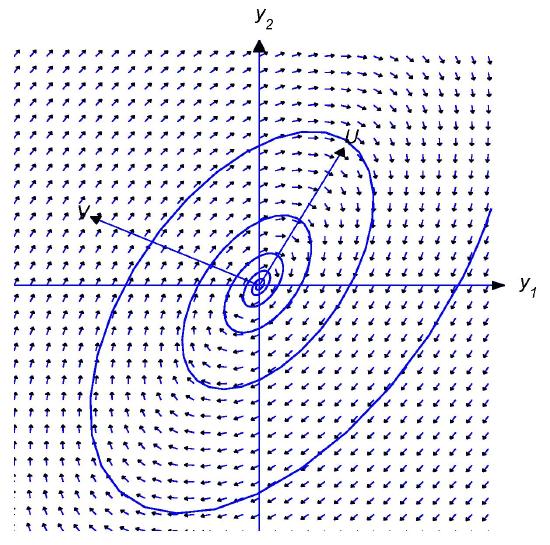
Figure \(4.6.6\)
\(\alpha<0\); shadow trajectory spiraling inward