5.1E:

Last updated
Save as PDF

Page ID: 26282

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Exercise $\PageIndex{1}$

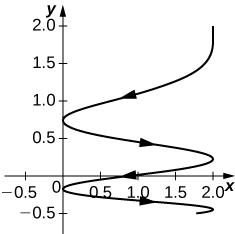
1) Give the component functions $\mathrm{x=f(t)}$ and $\mathrm{y=g(t)}$ for the vector-valued function $\mathrm{r(t)=3 \sec t \mathbf{i}+2 \tan t \mathbf{j}}$.

Given $\mathrm{r(t)=3 \sec t \mathbf{i}+2 \tan t \mathbf{j}}$, find the following values (if possible).

$\mathrm{r(\frac{\pi}{4})}$
$\mathrm{r(\pi)}$
$\mathrm{r(\frac{\pi}{2})}$

Sketch the curve of the vector-valued function $\mathrm{r(t)=3 \sec t \mathbf{i}+2 \tan t \mathbf{j}}$ and give the orientation of the curve. Sketch asymptotes as a guide to the graph.

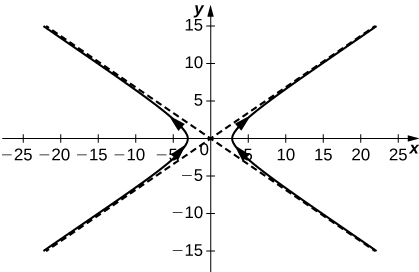
$This figure is the graph of the function r(t) = 3sect i + 2tant j. The graph has two slant asymptotes. They are diagonal and pass through the origin. The curve has two parts, one to the left of the y-axis with a hyperbolic bend. Also, there is a second part of the curve to the right of the y-axis with a hyperbolic bend. The orientation is represented by arrows on the curve. Both curves have orientation that is rising.$

Evaluate $\mathrm{\lim \limits_{t \to 0}⟨e^t \mathbf{i}+\frac{\sin t}{t} \mathbf{j}+e^{−t} \mathbf{k}⟩}$

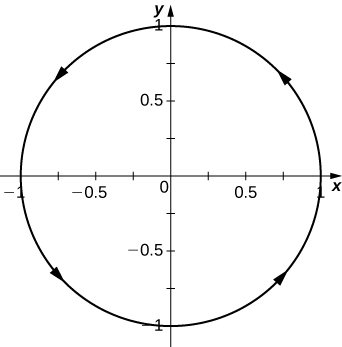
3) Given the vector-valued function $\mathrm{r(t)=⟨\cos t,\sin t⟩}$ find the following values:

$\mathrm{\lim \limits_{t \to \frac{\pi}{4}} r(t)}$
$\mathrm{r(\frac{\pi}{3})}$
Is $\mathrm{r(t)}$ continuous at $\mathrm{t=\frac{\pi}{3}}$?
Graph $\mathrm{r(t)}$.

Answer

3) a. $\mathrm{⟨\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}}$⟩, b. ⟨$\mathrm{\frac{1}{2},\frac{\sqrt{3}}{2}}$⟩, c. Yes, the limit as t approaches $\mathrm{\frac{\pi}{3}}$ is equal to $\mathrm{r(\frac{\pi}{3})}$, d.

$This figure is a graph of a circle centered at the origin. The circle has radius of 1 and has counter-clockwise orientation with arrows representing the orientation.$

Exercise $\PageIndex{2}$

1) Given the vector-valued function $\mathrm{r(t)=⟨t,t^2+1⟩}$, find the following values:

$\mathrm{\lim \limits_{t \to -3} r(t)}$
$\mathrm{r(−3)} $
Is $\mathrm{r(t)}$ continuous at $\mathrm{x=−3}$?
$\mathrm{r(t+2)−r(t)}$

2) Let $\mathrm{r(t)=e^t \mathbf{i}+\sin t \mathbf{j}+\ln t \mathbf{k}}$. Find the following values:

$\mathrm{r(\frac{\pi}{4})}$
$\mathrm{\lim \limits_{t \to \frac{\pi}{4} } r(t)}$
Is $\mathrm{r(t)}$ continuous at $\mathrm{t=t=\frac{\pi}{4}}$?

Answer: a. ⟨$\mathrm{e^{\frac{\pi}{4}},\frac{\sqrt{2}}{2},\ln (\frac{\pi}{4})}$⟩; b. ⟨$\mathrm{e^{\frac{\pi}{4}},\frac{\sqrt{2}}{2},\ln (\frac{\pi}{4})}$⟩; c. Yes

Exercise $\PageIndex{3}$

Find the limit of the following vector-valued functions at the indicated value of t.

1) $\mathrm{\lim \limits_{t \to 4}⟨\sqrt{t−3},\frac{\sqrt{t}−2}{t−4},\tan(\frac{\pi}{t})⟩}$

2) $\mathrm{\lim \limits_{t \to \frac{\pi}{2}} r(t)}$ for $\mathrm{r(t)=e^t \mathbf{i}+\sin t \mathbf{j}+\ln t \mathbf{k}}$

3) $\mathrm{\lim \limits_{t \to \infty}⟨e^{−2t},\frac{2t+3}{3t−1},\arctan(2t)⟩}$

4) $\mathrm{\lim \limits_{t \to e^2}⟨t \ln (t),\frac{\ln t}{t^2},\sqrt{\ln(t^2)⟩}}$

5) $\mathrm{\lim \limits_{t \to \frac{\pi}{6}}⟨\cos 2t,\sin 2t,1⟩}$

6) $\mathrm{\lim \limits_{t \to \infty} r(t)}$ for $\mathrm{r(t)=2e^{−t} \mathbf{ i}+e^{−t} \mathbf{j}+\ln(t−1) \mathbf{k}}$

Answer

2) $\mathrm{⟨e^{\frac{\pi}{2}},1,\ln(\frac{\pi}{2})⟩}$

4) $\mathrm{2e^2 \mathbf{i}+\frac{2}{e^4}\mathbf{j}+2\mathbf{k}}$

6) The limit does not exist because the limit of $\mathrm{\ln(t−1)}$ as t approaches infinity does not exist.

Exercise $\PageIndex{4}$

Describe the curve defined by the vector-valued function $\mathrm{r(t)=(1+t)\mathbf{i}+(2+5t)\mathbf{j}+(−1+6t)\mathbf{k}}$.

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{5}$

Find the domain of the vector-valued functions.

1) $\mathrm{r(t)=⟨t^2,\tan t,\ln t⟩}$

2) $\mathrm{r(t)=⟨t^2,\sqrt{t−3},\frac{3}{2t+1}⟩}$

3) $\mathrm{r(t)=⟨\csc(t),\frac{1}{\sqrt{t−3}}, \ln(t−2)⟩}$

Answer

1) $\mathrm{t>0,t≠(2k+1)\frac{\pi}{2}}$, where k is an integer.

3) $\mathrm{t>3,t≠n\pi}$, where n is an integer.

Exercise $\PageIndex{6}$

Let $\mathrm{r(t)=⟨\cos t,t,\sin t⟩}$ and use it to answer the following questions.

For what values of t is $\mathrm{r(t)}$ continuous?

Sketch the graph of $\mathrm{r(t)}$.

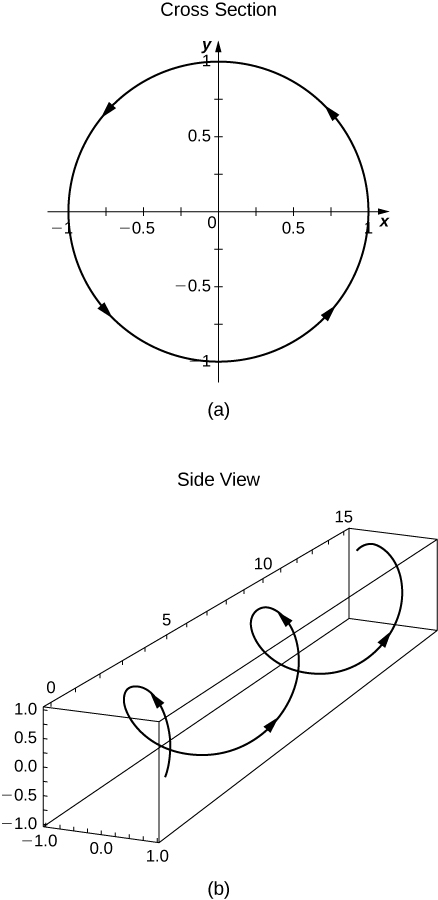
Answer: $This figure has two graphs. The first graph is labeled “cross section” and is a circle centered at the origin with radius of 1. It has counter-clockwise orientation. The section graph is labeled “side view” and is a 3 dimensional helix. The helix has counterclockwise orientation.$

Exercise $\PageIndex{7}$

1) Find the domain of $\mathrm{r(t)=2e^{-t} \mathbf{i}+e^{−t}\mathbf{j}+\ln(t−1)\mathbf{k}}$.

2) For what values of t is $\mathrm{r(t)=2e_S^{-t} \mathbf{i}+e^{−t}\mathbf{j}+\ln(t−1)\mathbf{k}}$ continuous?

Answer: 2) All t such that $\mathrm{t∈(1,\infty)}$

Exercise $\PageIndex{8}$

Eliminate the parameter t, write the equation in Cartesian coordinates, then sketch the graphs of the vector-valued functions. (Hint: Let $\mathrm{x=2t}$ and $\mathrm{y=t^2}$ Solve the first equation for x in terms of t and substitute this result into the second equation.)

1) $\mathrm{r(t)=2t\mathbf{i}+t^2 \mathbf{j}}$

2) $\mathrm{r(t)=t^3 \mathbf{i}+2t \mathbf{j}}$

3) $\mathrm{r(t)=2(\sinh t)\mathbf{i}+2(\cosh t) \mathbf{j},t>0}$

4) $\mathrm{r(t)=3(cost)i+3(sint)j}$

5) $\mathrm{r(t)=⟨3 \sin t,3 \cos t⟩}$

Answer

2) $\mathrm{y=2\sqrt[3]{x}}$, a variation of the cube-root function

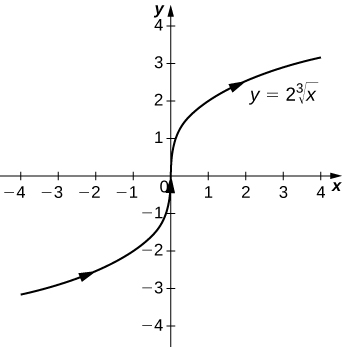
$This figure is the graph of y = 2 times the cube root of x. It is an increasing function passing through the origin. The curve becomes more vertical near the origin. It has orientation to the right represented with arrows on the curve.$

$\mathrm{x^2+y^2=9}$, a circle centered at $\mathrm{(0,0)}$ with radius 3, and a counterclockwise orientation

$This figure is the graph of x^2 + y^2 = 9. It is a circle centered at the origin with radius 3. It has orientation counter-clockwise represented with arrows on the curve.$

Exercise $\PageIndex{9}$

Use a graphing utility to sketch each of the following vector-valued functions:

1) [T] $\mathrm{r(t)=2 \cos t^2 \mathbf{i}+(2−\sqrt{t})\mathbf{j}}$

2) [T] $\mathrm{r(t)=⟨e^{\cos (3t)},e^{−\sin(t)}⟩}$

3) [T] $\mathrm{r(t)=⟨2−\sin (2t),3+2 \cos t⟩}$

Answer

1) $This figure is the graph of r(t) = 2cost^2 i + (2 – the square root of t) j. The curve spirals in the first quadrant, touching the y-axis. As the curve gets closer to the x-axis, the spirals become tighter. It has the look of a spring being compressed. The arrows on the curve represent orientation going downward.$

$This figure has two graphs. The first is 3 dimensional and is a curve making a figure eight on its side inside of a box. The box represents the first octant. The second graph is 2 dimensional. It represents the same curve from a “view in the yt plane”. The horizontal axis is labeled “t”. The curve is connected and crosses over itself in the first quadrant resembling a figure eight.$

Exercise $\PageIndex{10}$

Find a vector-valued function that traces out the given curve in the indicated direction.

1) $\mathrm{4x^2+9y^2=36}$; clockwise and counterclockwise

2) $\mathrm{r(t)=⟨t,t^2⟩}$; from left to right

Answer: 2) For left to right, $\mathrm{y=x^2}$, where t increases.

Exercise $\PageIndex{11}$

Consider the curve described by the vector-valued function $\mathrm{r(t)=(50e^{−t}\cos t)\mathbf{i}+(50e^{−t}\sin t)\mathbf{j}+(5−5e^{−t})\mathbf{k}}$.

1) What is the initial point of the path corresponding to $\mathrm{r(0)}$?

2) What is $\mathrm{\lim \limits_{t \to \infty}r(t)} $?

3) [T] Use technology to sketch the curve.

Answer

1) $\mathrm{(50,0,0)}$

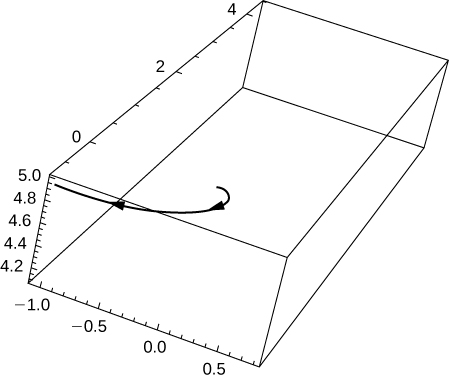
2) $This figure is a graph in the 3 dimensional coordinate system. It is a curve starting at the middle of the box and curving towards the upper left corner The box represents an octant of the coordinate system.$

Exercise $\PageIndex{11}$

Consider the curve described by the vector-valued function $\mathrm{r(t)=(50e^{−t}\cos t)\mathbf{i}+(50e^{−t}\sin t)\mathbf{j}+(5−5e^{−t})\mathbf{k}}$.

1) What is the initial point of the path corresponding to $\mathrm{r(0)}$?

2) What is $\mathrm{\lim \limits_{t \to \infty}r(t)} $?

3) [T] Use technology to sketch the curve.

4) Eliminate the parameter t to show that $\mathrm{z=5−\frac{r}{10}}$ where $\mathrm{r=x^2+y^2}$.

Answer

1) $\mathrm{(50,0,0)}$

3) $This figure is a graph in the 3 dimensional coordinate system. It is a curve starting at the middle of the box and curving towards the upper left corner The box represents an octant of the coordinate system.$

Exercise $\PageIndex{12}$

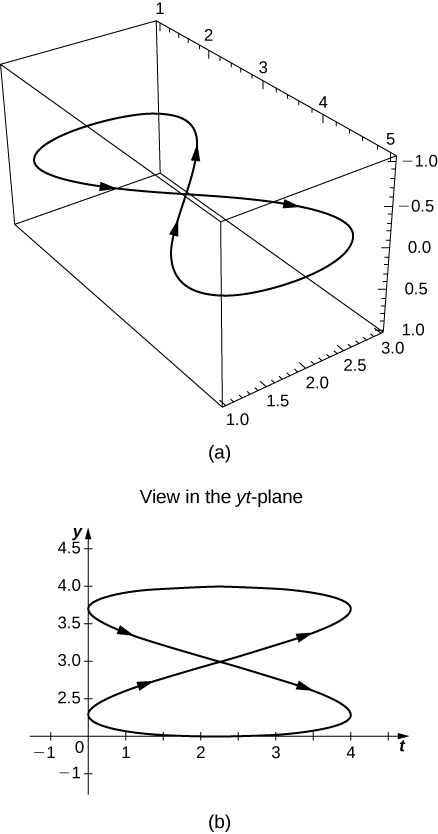
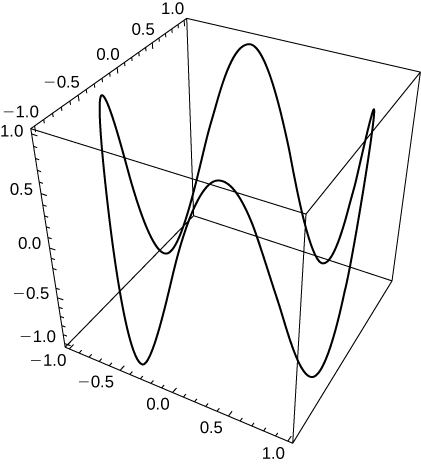
1) [T] Let $\mathrm{r(t)=\cos t \mathbf{i}+\sin t\mathbf{j}+0.3 \sin (2t)\mathbf{k}}$. Use technology to graph the curve (called the roller-coaster curve) over the interval $\mathrm{[0,2\pi)}$. Choose at least two views to determine the peaks and valleys.

2) [T] Use the result of the preceding problem to construct an equation of a roller coaster with a steep drop from the peak and steep incline from the “valley.” Then, use technology to graph the equation.

3) Use the results of the preceding two problems to construct an equation of a path of a roller coaster with more than two turning points (peaks and valleys).

Answer

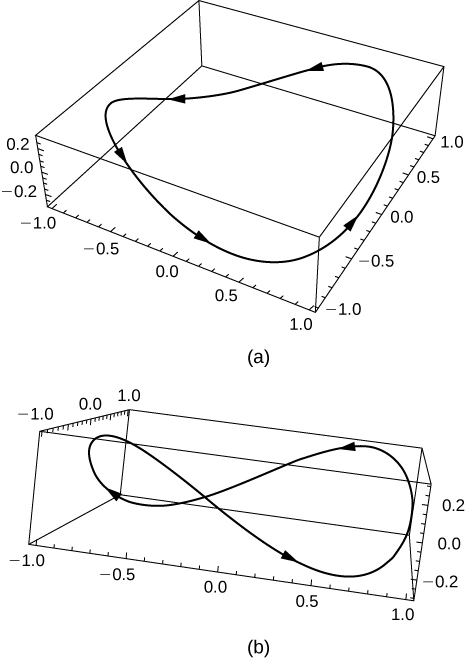
1) $This figure has two graphs. The first is 3 dimensional and is a connected curve with counter-clockwise orientation inside of a box. The second graph is 3 dimensional. It represents the same curve from different view of the box. From the side of the box the curve is connected and has depth to it.$

One possibility is $\mathrm{r(t)=\cos t \mathbf{i}+\sin t\mathbf{j}+\sin (4t)\mathbf{k}}$. By increasing the coefficient of t in the third component, the number of turning points will increase.

$This figure is a 3 dimensional graph. It is a connected curve inside of a box. The curve has orientation. As the orientation travels around the curve, it does go up and down in depth.$

Exercise $\PageIndex{13}$

Graph the curve $\mathrm{r(t)=(4+cos(18t))\cos(t)\mathbf{i}+(4+\cos (18t)sin(t))\mathbf{j}+0.3 \sin(18t)\mathbf{k}}$ using two viewing angles of your choice to see the overall shape of the curve.
Does the curve resemble a “slinky”?
What changes to the equation should be made to increase the number of coils of the slinky?

Search

Text Color

Text Size

Margin Size

Font Type

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)