6.7E:

Last updated
Save as PDF

Page ID: 25953

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Exercise $\PageIndex{1}$

Finding Critical Points

For the following exercises, find all critical points.

1) $\displaystyle f(x,y)=1+x^2+y^2$

Answer: $ (0,0)$

2) $\displaystyle f(x,y)=(3x−2)^2+(y−4)^2$

Answer: $\displaystyle (\frac{2}{3},4)$

3) $\displaystyle f(x,y)=x^4+y^4−16xy$

4) $\displaystyle f(x,y)=15x^3−3xy+15y^3$

Answer

$\displaystyle (0,0) (\frac{1}{15},\frac{1}{15})$

5)$ f(x, y) = 1 - (x -2)^2 + (y+3)^2$

Exercise $\PageIndex{2}$

For the following exercises, find the critical points of the function by using algebraic techniques (completing the square) or by examining the form of the equation. Verify your results using the partial derivatives test.

6) $\displaystyle f(x,y)=\sqrt{x^2+y^2}$

Answer: Crit. pts.: $ (0, 0) $
Extrema: $ f$ has a relative maximum of $0$ at $ (0, 0)$.
To justify this, consider the fact that the square root function cannot give a negative value, so this function cannot possibly return a positive value. Since it's value is $0$ at the critical point $ (0, 0)$, we know it must be the function's absolute maximum value.

7) $\displaystyle f(x,y)=−x^2−5y^2+8x−10y−13$

Answer: Maximum at $\displaystyle (4,−1,8)$

8) $\displaystyle f(x,y)=x^2+y^2+2x−6y+6$

9) $\displaystyle f(x,y)=\sqrt{x^2+y^2}+1$

Answer: Crit. Pts.: $ (0, 0) $
Extrema: $ f$ has a relative minimum of $1$ at $ (0,0)$.
To justify this, consider the fact that the square root function cannot give a negative value, so this function cannot possibly return a value less than $1$. Since it's value is $1$ at the critical point $ (0, 0)$, we know $1$ must be the function's absolute minimum value.

Exercise $\PageIndex{3}$

For the following exercises, use the second derivative test to identify any critical points and determine whether each critical point is a maximum, minimum, saddle point, or none of these.

10) $\displaystyle f(x,y)=−x^3+4xy−2y^2+1$

11) $\displaystyle f(x,y)=x^2y^2$

Answer: Crit. pts.: All points on the lines $ x = 0 $ and $ y = 0$ are critical points of this function.
Exrema: The Second Partials Test fails.
Since $ x^2y^2>0$ for all $ x$ and $ y$ different from zero, and $ x^2y^2=0$ when either $ x$ or $ y$ equals zero (or both), then the absolute minimum of $0$ occurs at all points on the $x$- or $y$-axes, that is, for all points on the lines $ x = 0 $ and $ y = 0$.

12) $\displaystyle f(x,y)=x^2−6x+y^2+4y−8$

13) $\displaystyle f(x,y)=2xy+3x+4y$

Answer: Crit. pts.: $ \left(−2,−\frac{3}{2}\right) $
Exrema: $f$ has a saddle point at $ \left(−2,−\frac{3}{2},−6\right) $.

14) $\displaystyle f(x,y)=8xy(x+y)+7$

15) $\displaystyle f(x,y)=x^2+4xy+y^2$

Answer: Crit. pts.: $ (0,0) $
Exrema: $f$ has a saddle point at $ (0,0,0)$.

16) $\displaystyle f(x,y)=x^3+y^3−300x−75y−3$

17) $\displaystyle f(x,y)=9−x^4y^4$

Answer: Crit. pts.: All points on the lines $ x = 0 $ and $ y = 0$ are critical points of this function.
Extrema: The Second Partials Test fails.
Since the term $ -x^4y^4<0$ for all $ x$ and $ y$ different from zero, and $ -x^4y^4=0$ when either $ x$ or $ y$ equals zero (or both), then this function cannot attain a value greater than $9$ anywhere, but is $9$ at the critical points. Thus $f$ has an absolute maximum of $9$ at all points on the $x$- or $y$-axes, that is, for all points on the lines $ x = 0 $ and $ y = 0$.

18) $ f(x,y)=x^2+10xy+y^2$

Answer: Crit. pts.: $ (0,0) $
Extrema: $f$ has a saddle point at $ (0,0,0)$.

19) $f(x,y) = x^4 + y^2 + 2xy + 3$

Answer: Crit. pts.: $ (0,0), \quad \left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right), \quad \left(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\right) $
Extrema: $f$ has a saddle point at $ (0, 0, 3) $,
$f$ has a local minimum of $ 2.75$ at the point $ \left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right) $.
$f$ has a local minimum of $ 2.75$ at the point $ \left(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\right) $.

20) $\displaystyle f(x,y)=7x^2y+9xy^2$

21) $\displaystyle f(x,y)=3x^2−2xy+y^2−8y$

Answer: Crit. pts.: $ (2,6) $
Extrema: $f$ has a relative minimum of $ -24$ located at $ (2,6)$.

22) $\displaystyle f(x,y)=3x^2+2xy+y^2$

23) $\displaystyle f(x,y)=y2+xy+3y+2x+3$

Answer: Crit. pts.: $ (1,−2) $
Extrema: $f$ has a saddle point at $ (1,−2,1)$.

24) $\displaystyle f(x,y)=x^2+xy+y^2−3x$

25) $\displaystyle f(x,y)=x^2+2y^2−x^2y$

Answer: Crit. pts.: $ (0,0), \quad (-2,1), \quad (2,1)$
Extrema: $f$ has a relative minimum of $0$ at $ (0,0) $ and saddle points at $ (2,1,2)$ and $ (−2,1,2)$.

26) $\displaystyle f(x,y)=x^2+y−e^y$

27) $\displaystyle f(x,y)=e^{−(x^2+y^2+2x)}$

Answer: Crit. pts.: $ (-1,0) $
Extrema: $f$ has a relative maximum of $ e $ located at $ (-1,0)$.
See this problem illustrated in CalcPlot3D.

28) $\displaystyle f(x,y)=x^2+xy+y^2−x−y+1$

29) $\displaystyle f(x,y)=x^2+10xy+y^2$

Answer: $(0,0)$ is a saddle point.

30) $\displaystyle f(x,y)=−x^2−5y^2+10x−30y−62$

31) $\displaystyle f(x,y)=120x+120y−xy−x^2−y^2$

Answer: Crit. pts.: $ (40,40) $
Extrema: $f$ has a relative maximum of $ 4800 $ located at $ (40,40)$.

32) $\displaystyle f(x,y)=2x^2+2xy+y^2+2x−3$

33) $\displaystyle f(x,y)=x^2+x−3xy+y^3−5$

Answer: Crit. pts.: $ \left(\frac{1}{4},\frac{1}{2}\right)$ and $(1, 1) $
Extrema: $f$ has a saddle point at $ \left(\frac{1}{4},\frac{1}{2}, -\frac{79}{16}\right)$ and a relative minimum of $ -5 $ at $ (1,1)$.

34) $\displaystyle f(x,y)=2xye^{−x^2−y^2}$

Exercise $\PageIndex{4}$

For the following exercises, determine the extreme values and the saddle points. Use a CAS to graph the function.

35) [T] $\displaystyle f(x,y)=ye^x−e^y$

Answer

A saddle point is located at $\displaystyle (0,0).$

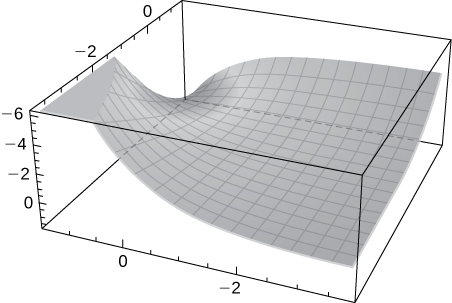
$A complicated graph that starts near (1, 1, 1), and decreases significantly along the x and y axes, so much so along the y axis that it is cut off. The rest of the graph stays near 0.$

36) [T] $\displaystyle f(x,y)=xsin(y)$

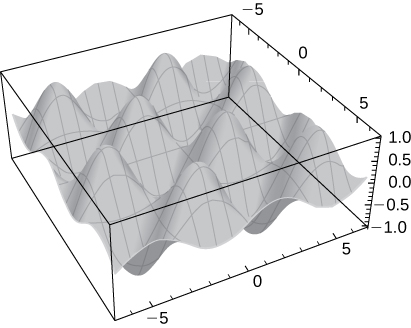
37) [T] $\displaystyle f(x,y)=sin(x)sin(y),x∈(0,2π),y∈(0,2π)$

Answer

There is a saddle point at $\displaystyle (π,π),$ local maxima at $\displaystyle (\frac{π}{2},\frac{π}{2})$ and $\displaystyle (\frac{3π}{2},\frac{3π}{2})$, and local minima at $\displaystyle (\frac{π}{2},\frac{3π}{2})$ and $\displaystyle (\frac{3π}{2},\frac{π}{2})$.

$A series of hills and holes alternating through a space with amplitude 1.$

Exercise $\PageIndex{5}$

Find the absolute extrema of the given function on the indicated closed and bounded set $\displaystyle R$.

38) $\displaystyle f(x,y)=xy−x−3y; R$ is the triangular region with vertices $\displaystyle (0,0),(0,4),$ and $\displaystyle (5,0)$.

39) Find the absolute maximum and minimum values of $\displaystyle f(x,y)=x^2+y^2−2y+1$ on the region $\displaystyle R={(x,y)∣x^2+y^2≤4}.$

Answer: $\displaystyle (0,1,0)$ is the absolute minimum and $\displaystyle (0,−2,9)$ is the absolute maximum.

40) $\displaystyle f(x,y)=x^3−3xy−y^3$ on $\displaystyle R={(x,y):−2≤x≤2,−2≤y≤2}$

41) $\displaystyle f(x,y)=\frac{−2y}{x^2+y^2+1}$ on $\displaystyle R={(x,y):x^2+y^2≤4}$

Answer: There is an absolute minimum at $\displaystyle (0,1,−1)$ and an absolute maximum at $\displaystyle (0,−1,1)$.

Exercise $\PageIndex{6}$

42) Find three positive numbers the sum of which is $\displaystyle 27$, such that the sum of their squares is as small as possible.

43) Find the points on the surface $\displaystyle x^2−yz=5$ that are closest to the origin.

Answer: $\displaystyle (\sqrt{5},0,0),(−\sqrt{5},0,0)$

44) Find the maximum volume of a rectangular box with three faces in the coordinate planes and a vertex in the first octant on the line $\displaystyle x+y+z=1$.

45) The sum of the length and the girth (perimeter of a cross-section) of a package carried by a delivery service cannot exceed $\displaystyle 108$ in. Find the dimensions of the rectangular package of largest volume that can be sent.

Answer: $\displaystyle 18$ by $\displaystyle 36$ by $\displaystyle 18$ in.

46) A cardboard box without a lid is to be made with a volume of $\displaystyle 4$ ft³. Find the dimensions of the box that requires the least amount of cardboard.

47) Find the point on the surface $\displaystyle f(x,y)=x^2+y^2+10$ nearest the plane $\displaystyle x+2y−z=0.$ Identify the point on the plane.

Answer: $\displaystyle (\frac{47}{24},\frac{47}{12},\frac{235}{24})$

48) Find the point in the plane $\displaystyle 2x−y+2z=16$ that is closest to the origin.

49) A company manufactures two types of athletic shoes: jogging shoes and cross-trainers. The total revenue from $\displaystyle x$ units of jogging shoes and $\displaystyle y$ units of cross-trainers is given by $\displaystyle R(x,y)=−5x^2−8y^2−2xy+42x+102y,$ where $\displaystyle x$ and $\displaystyle y$ are in thousands of units. Find the values of $\displaystyle x$ and $\displaystyle y$ to maximize the total revenue.

Answer: $\displaystyle x=3$ and $\displaystyle y=6$

50) A shipping company handles rectangular boxes provided the sum of the length, width, and height of the box does not exceed $\displaystyle 96$in. Find the dimensions of the box that meets this condition and has the largest volume.

51) Find the maximum volume of a cylindrical soda can such that the sum of its height and circumference is $\displaystyle 120$ cm.

Answer: $\displaystyle V=\frac{64,000}{π}≈20,372cm^3$

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Paul Seeburger (Monroe Community College) created problems 19 and 29, and added dynamic figures for problems 27 and 35.

Search

Text Color

Text Size

Margin Size

Font Type

Finding Critical Points

Exercise \(\PageIndex{1}\)

Finding Critical Points

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Contributors