9.2E: Exercises
- Page ID
- 26273
Exercise \(\PageIndex{1}\)
1. True or False? Line integral \(\displaystyle \int _C f(x,y)ds\) is equal to a definite integral if \( C \) is a smooth curve defined on \([a,b]\) and if function \(f \) is continuous on some region that contains curve \( C \).
- Answer
-
True
2. True or False? Vector functions \(\vecs{r_1}= t \, \hat{\mathbf i}+ t^2 \, \hat{\mathbf j}, 0 \leq t \leq 1\) and \(\vecs{r_2}=(1- t) \, \hat{\mathbf i}+ (1- t)^2 \, \hat{\mathbf j}, 0 \leq t \leq 1\), define the same oriented curve.
3. True or False? \(\displaystyle \int _{−C}(Pdx+Qdy)=\displaystyle \int _C(Pdx−Qdy)\)
- Answer
-
False
4. True or False? A piecewise smooth curve \( C \) consists of a finite number of smooth curves that are joined together end to end.
5. True or False? If is given by \(x(t)=t,y(t)=t, 0≤t≤1\), then \(\displaystyle \int _Cxyds=\displaystyle \int ^1_0t^2dt.\)
- Answer
-
False
Exercise \(\PageIndex{2}\)
For the following exercises, use a computer algebra system (CAS) to evaluate the line integrals over the indicated path.
6. [T] \(\displaystyle \int _C(x+y)ds\), where \(C:x=t,y=(1−t),z=0\) from \((0, 1, 0)\) to \((1, 0, 0)\)
7. [T] \(\displaystyle \int _C(x−y)ds\), where \( C: \vecs{r}(t)= 4t \, \hat{\mathbf i} + 3 t \, \hat{\mathbf j} , 0 \leq t\leq 2.\)
- Answer
-
\(10\)
8. [T] \(\displaystyle \int _C(x^2+y^2+z^2)ds\) where \( C: \vecs{r}(t)= \sin(t) \, \hat{\mathbf i} + \cos(t) \, \hat{ \mathbf j}+ 8t \, \hat{\mathbf k} , 0 \leq t\leq \dfrac{π}{2}.\)
9. [T] Evaluate \(\displaystyle \int _Cxy^4ds\), where \( C \) is the right half of circle \(x^2+y^2=16\) and is traversed in the clockwise direction.
- Answer
-
\(\frac{8192}{5}\)
10. [T] Evaluate \(\displaystyle \int _C4x^3ds\), where \( C \) is the line segment from \((−2,−1)\) to \((1, 2)\).
Exercise \(\PageIndex{3}\)
For the following exercises, find the work done.
11. Find the work done by vector field \( \vecs{F}(x,y,z)= x \, \hat{\mathbf i} + 3xy \, \hat{ \mathbf j} -(x+z) \, \hat{\mathbf k} \) on a particle moving along a line segment that goes from \((1,4,2)\) to \((0,5,1)\).
- Answer
-
\(8\)
12. Find the work done by a person weighing 150 lb walking exactly one revolution up a circular, spiral staircase of radius 3 ft if the person rises 10 ft.
13. Find the work done by force field \( \vecs{F}(x,y,z)= −\dfrac{1}{2} x \, \hat{\mathbf i} −\dfrac{1}{2}y \, \hat{ \mathbf j} +\dfrac{1}{4} \, \hat{\mathbf k} \) on a particle as it moves along the helix \( \vecs{r}(t)= \cos(t) \, \hat{\mathbf i} + \sin(t) \, \hat{\mathbf j}+ t \, \hat{\mathbf k}\) from point \((1,0,0)\) to point \((−1,0,3π)\).
- Answer
-
\(W=\dfrac{3π}{4}\)
14. Find the work done by vector field \(\vecs{F}(x,y)= y \, \hat{\mathbf i} + 2x \, \hat{ \mathbf j}\) in moving an object along path \( C \), which joins points \((1, 0)\) and \((0, 1)\).
15. Find the work done by force \(\vecs{F}(x,y)= 2y \, \hat{\mathbf i} + 3x \, \hat{ \mathbf j}+ (x+y) \, \hat{\mathbf k}\) in moving an object along curve \( \vecs{r}(t)= \cos(t) \, \hat{\mathbf i} + \sin(t) \, \hat{ \mathbf j}+ 16 \, \hat{\mathbf k}\), where \(0≤t≤2π\).
- Answer
-
\(W=π\)
16. Find the mass of wire in the shape of a circle of radius 2 centred at (3, 4) with linear mass density \(ρ(x,y)=y^2\).
Exercise \(\PageIndex{4}\)
For the following exercises, evaluate the line integrals.
17. Evaluate \(\displaystyle \int _C \vecs{F}·\vecs{dr}\), where \(\vecs{F}(x,y)=− \, \hat{\mathbf j}\) and C is the part of the graph of \(y=12x^3−x\) from \((2,2)\) to \((−2,−2).\)
- Answer
-
\(4\)
18. Evaluate \(\displaystyle \int _C(x^2+y^2+z^2)^{−1}ds\), where \(C\) is the helix \(x=cost,y=sint,z=t, (0≤t≤T).\)
19. Evaluate \(\displaystyle \int _Cyzdx+xzdy+xydz\) over the line segment from \((1,1,1) \) to \((3,2,0).\)
- Answer
-
\(\displaystyle \int _Cyzdx+xzdy+xydz=−1\)
20. Let \( C \) be the line segment from point (0, 1, 1) to point (2, 2, 3). Evaluate line integral \(\displaystyle \int _Cyds.\)
21. [T] Use a computer algebra system to evaluate the line integral \(\displaystyle \int _Cy^2dx+xdy\), where C is the arc of the parabola \(x=4−y^2\) from \((−5, −3)\) to \((0, 2)\).
- Answer
-
\(\displaystyle \int _C(y^2)dx+(x)dy=\dfrac{245}{6}\)
22. [T] Use a computer algebra system to evaluate the line integral \(\displaystyle \int _C(x+3y^2)dy\) over the path \( C \) given by \(x=2t,y=10t,\) where \(0≤t≤1.\)
23. [T] Use a CAS to evaluate line integral \(\displaystyle \int _Cxydx+ydy\) over path \( C \) given by \(x=2t,y=10t\),where \(0≤t≤1\).
- Answer
-
\(\displaystyle \int _Cxydx+ydy=\dfrac{190}{3}\)
24. Evaluate line integral \(\displaystyle \int _C(2x−y)dx+(x+3y)dy\), where \( C \)lies along the x-axis from \(x=0\) to \(x=5\).
26. [T] Use a CAS to evaluate \(\displaystyle \int _C\dfrac{y}{2x^2−y^2}ds\), where \( C \) is \(x=t,y=t,1≤t≤5.\)
- Answer
-
\(\displaystyle \int _C\dfrac{y}{2x^2−y^2}ds=\sqrt{2}ln5\)
27. [T] Use a CAS to evaluate \(\displaystyle \int _C xyds, \) where \( C \) is \(x=t^2,y=4t,0≤t≤1.\)
Exercise \(\PageIndex{5}\)
In the following exercises, find the work done by force field \(\vecs{F} \) on an object moving along the indicated path.
28. \( \vecs{F}(x,y)=−x \, \hat{\mathbf i}−2y \, \hat{\mathbf j} \)
\(C:y=x^3\) from \((0, 0)\) to \((2, 8)\)
- Answer
-
\(W=−66\)
29. \(\vecs{F}(x,y)=2x \, \hat{\mathbf i}+y \, \hat{\mathbf j}\)
\( C \): counterclockwise around the triangle with vertices \((0, 0), (1, 0), \) and \((1, 1)\)
30. \(\vecs{F}(x,y,z)=x \, \hat{\mathbf i}+y \, \hat{\mathbf j}−5z \, \hat{\mathbf k}\)
\(C:\vecs{r}(t)=2cost \, \hat{\mathbf i}+2sint \, \hat{\mathbf j}+t \, \hat{\mathbf k},0≤t≤2π\)
- Answer
-
\(W=−10π^2\)
Exercise \(\PageIndex{6}\)
31. Let \(\vecs{F}\) be vector field \(\vecs{F}(x,y)=(y^2+2xe^y+1) \, \hat{\mathbf i}+(2xy+x^2e^y+2y) \, \hat{\mathbf j}\). Compute the work of integral \(\displaystyle \int _C\vecs{F}·\vecs{dr}\), where \( C \) is the path \(\vecs{r}(t)=sint \, \hat{\mathbf i}+cost \, \hat{\mathbf j}, 0≤t≤\dfrac{π}{2}\).
32. Compute the work done by force \(\vecs{F}(x,y,z)=2x \, \hat{\mathbf i}+3y \, \hat{\mathbf j}−zk\) along path \(\vecs{r}(t)=t \, \hat{\mathbf i}+t^2 \, \hat{\mathbf j}+t^3 \, \hat{\mathbf k}\),where \(0≤t≤1\).
- Answer
-
\(W=2\)
33. Evaluate \(\displaystyle \int _C \vecs{F}·\vecs{dr}\), where \(\vecs{F}(x,y)=\dfrac{1}{x+y} \, \hat{\mathbf i}+\dfrac{1}{x+y} \, \hat{\mathbf j}\) and \( C \) is the segment of the unit circle going counterclockwise from \((1,0)\) to \((0, 1)\).
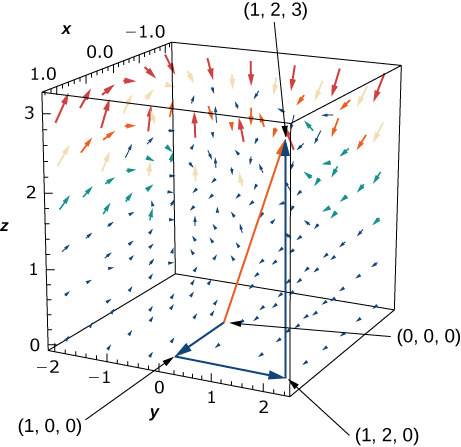
34. Force \(\vecs{F}(x,y,z)=zy \, \hat{\mathbf i}+x \, \hat{\mathbf j}+z^2x \, \hat{\mathbf k}\) acts on a particle that travels from the origin to point \((1, 2, 3). \) Calculate the work done if the particle travels:
- along the path \((0,0,0)→(1,0,0)→(1,2,0)→(1,2,3)\) along straight-line segments joining each pair of endpoints;
- along the straight line joining the initial and final points.
- Is the work the same along the two paths?
- Answer
-
a. \(W=11\); b. \(W=11\); c. Yes
35. Find the work done by vector field \(\vecs{F}(x,y,z)=x \, \hat{\mathbf i}+3xy \, \hat{\mathbf j}−(x+z) \, \hat{\mathbf k}\) on a particle moving along a line segment that goes from \((1, 4, 2)\) to \((0, 5, 1).\)
36. How much work is required to move an object in vector field \(\vecs{F}(x,y)=yi+3x \, \hat{\mathbf j}\) along the upper part of ellipse \(\dfrac{x^2}{4}+y^2=1\) from \((2, 0)\) to \((−2,0)\)?
- Answer
-
\(W=2π\)
37. A vector field is given by \(\vecs{F}(x,y)=(2x+3y)i+(3x+2y) \, \hat{\mathbf j}\). Evaluate the line integral of the field around a circle of unit radius traversed in a clockwise fashion.
38. Evaluate the line integral of scalar function xy along parabolic path \(y=x^2\) connecting the origin to point \((1, 1)\).
- Answer
-
\(\displaystyle \int _C \vecs{F}·\vecs{dr}=\dfrac{25\sqrt{5}+1}{120}\)
39. Find \(\displaystyle \int _Cy^2dx+(xy−x^2)dy\) along \(C: y=3x\) from (0, 0) to (1, 3).
40. Find \(\displaystyle \int _Cy^2dx+(xy−x^2)dy\) along \(C: y^2=9x\) from (0, 0) to (1, 3).
- Answer
-
\(\displaystyle \int _Cy^2dx+(xy−x^2)dy=6.15\)
Exercise \(\PageIndex{7}\)
For the following exercises, use a CAS to evaluate the given line integrals.
41. [T] Evaluate \(\vecs{F}(x,y,z)=x^2z \, \hat{\mathbf i}+6y \, \hat{\mathbf j}+yz^2 \, \hat{\mathbf k}\), where \(C\) is represented by \(\vecs{r}(t)=t \, \hat{\mathbf i}+t^2 \, \hat{\mathbf j}+lnt \, \hat{\mathbf k},1≤t≤3\).
42. [T] Evaluate line integral \(\displaystyle \int _Cxe^yds\) where, \(C\) is the arc of curve \(x=e^y\) from \((1,0)\) to \((e,1)\).
- Answer
-
\(\displaystyle \int _Cxe^yds≈7.157\)
43. [T] Evaluate the integral \(\displaystyle \int _Cxy^2ds\), where \(C\) is a triangle with vertices \((0, 1, 2), (1, 0, 3)\), and \((0,−1,0)\).
44. [T] Evaluate line integral \(\displaystyle \int _C(y^2−xy)dx\), where \(C\) is curve \(y=lnx\) from \((1, 0)\) toward \((e,1)\).
- Answer
-
\(\displaystyle \int _C(y^2−xy)dx≈−1.379\)
45. [T] Evaluate line integral \(\displaystyle \int_C xy^4ds,\) where \(C\) is the right half of circle \(x^2+y^2=16.\)
46. [T] Evaluate \(\displaystyle \int_C\vecs{F}⋅\vecs{dr}\), where \(\vecs{F}(x,y,z)=x^2y \, \hat{\mathbf i}+(x−z) \, \hat{\mathbf j}+xyz \, \hat{\mathbf k}\) and
\(C: \vecs{r}(t)=t \, \hat{\mathbf i}+t^2 \, \hat{\mathbf j}+2 \, \hat{\mathbf k}, 0≤t≤1\).
- Answer
-
\(\displaystyle \int _C\vecs{F}⋅\vecs{dr}≈−1.133\)
47. Evaluate \(\displaystyle \int_C\vecs{F}⋅\vecs{dr}\), where \(\vecs{F}(x,y)=2xsin(y)i+(x^2cos(y)−3y^2) \, \hat{\mathbf j}\) and
\(C\) is any path from \((−1,0)\) to \((5, 1)\).
48. Find the line integral of \(\vecs{F}(x,y,z)=12x^2 \, \hat{\mathbf i}−5xy \, \hat{\mathbf j}+xz \, \hat{\mathbf k}\) over path \(C\) defined by \(y=x^2, z=x^3\) from point \((0, 0, 0)\) to point \((2, 4, 8)\).
- Answer
-
\(\displaystyle \int _C\vecs{F}⋅\vecs{dr}≈22.857\)
49. Find the line integral of \(\displaystyle \int _C(1+x^2y)ds\), where \(C\) is ellipse \(\vecs{r}(t)=2cost \, \hat{\mathbf i}+3sint \, \hat{\mathbf j}\) from \(0≤t≤π.\)
- Answer
-
TBA
Exercise \(\PageIndex{8}\)
For the following exercises, find the flux.
50. Compute the flux of \(\vecs{F}=x^2 \, \hat{\mathbf i}+y \, \hat{\mathbf j}\) across a line segment from \((0, 0)\) to \((1, 2).\)
- Answer
-
\(Flux=−\dfrac{1}{3}\)
51. Let \(\vecs{F}=5 \, \hat{\mathbf i}\) and let \(C\) be curve \(y=0,0≤x≤4\). Find the flux across \(C\).
52. Let \(\vecs{F}=5 \, \hat{\mathbf j}\) and let \(C\) be curve \(y=0,0≤x≤4\). Find the flux across \(C\).
- Answer
-
\(Flux=−20\)
53. Let \(\vecs{F}=−y \, \hat{\mathbf i}+x \, \hat{\mathbf j}\) and let \(C: \vecs{r}(t)=cost \, \hat{\mathbf i}+sint \, \hat{\mathbf j} (0≤t≤2π)\). Calculate the flux across \(C\).
54. Let \(\vecs{F}=(x^2+y^3) \, \hat{\mathbf i}+(2xy) \, \hat{\mathbf j}\). Calculate flux orientated counterclockwise across curve \(C : x^2+y^2=9.\)
- Answer
-
\(Flux=0\)
Exercise \(\PageIndex{9}\)
55. Find the line integral of \(\displaystyle \int _Cz^2dx+ydy+2ydz,\) where \(C\) consists of two parts: \(C_1\) and \(C_2. C_1\) is the intersection of cylinder \(x^2+y^2=16\) and plane \(z=3\) from \((0, 4, 3)\) to \((−4,0,3). C_2\) is a line segment from \((−4,0,3)\) to \((0, 1, 5)\).
56. A spring is made of a thin wire twisted into the shape of a circular helix \(x=2cost, y=2sint, z=t.\) Find the mass of two turns of the spring if the wire has constant mass density.
- Answer
-
\(m=4πρ\sqrt{5}\)
57. A thin wire is bent into the shape of a semicircle of radius a. If the linear mass density at point P is directly proportional to its distance from the line through the endpoints, find the mass of the wire.
58. An object moves in force field \(\vecs{F}(x,y,z)=y^2 \, \hat{\mathbf i}+2(x+1)y \, \hat{\mathbf j}\) counterclockwise from point \((2, 0)\) along elliptical path \(x^2+4y^2=4\) to \((−2,0)\), and back to point \((2, 0)\) along the x-axis. How much work is done by the force field on the object?
- Answer
-
\(W=0\)
59. Find the work done when an object moves in force field \(\vecs{F}(x,y,z)=2x \, \hat{\mathbf i}−(x+z) \, \hat{\mathbf j}+(y−x) \, \hat{\mathbf k}\) along the path given by \(\vecs{r}(t)=t^2 \, \hat{\mathbf i}+(t^2−t) \, \hat{\mathbf j}+3 \, \hat{\mathbf k}, 0≤t≤1.\)
60. If an inverse force field \(\vecs{F}\) is given by \(\vecs{F}(x,y,z)=\dfrac{k}{‖r‖^3}r\), where \( k\) is a constant, find the work done by \(\vecs{F}\) as its point of application moves along the x-axis from \(A(1,0,0)\) to \(B(2,0,0)\).
- Answer
-
\(W=\dfrac{k}{2}\)
61. David and Sandra plan to evaluate line integral \(\displaystyle \int _C \vecs{F}·\vecs{dr}\) along a path in the xy-plane from (0, 0) to (1, 1). The force field is \(\vecs{F}(x,y)=(x+2y) \, \hat{\mathbf i}+(−x+y^2) \, \hat{\mathbf j}\). David chooses the path that runs along the x-axis from (0, 0) to (1, 0) and then runs along the vertical line x=1 from (1, 0) to the final point (1, 1). Sandra chooses the direct path along the diagonal line \(y=x\) from (0, 0) to (1, 1). Whose line integral is larger and by how much?
- Answer
-
Add texts here. Do not delete this text first.


