9.3E: EXERCISES

Exercise $\PageIndex{1}$: True or False?

1. If vector field $\vecs{F}$ is conservative on the open and connected region D, then line integrals of $\vecs{F}$ are path independent on D, regardless of the shape of D.

2. The Function $r(t)=a+t(b−a)$, where $0≤t≤1$, parameterizes the straight-line segment from a to b.

3. The vector field $\vecs{F}(x,y,z)=(y sinz) \, \hat{ \mathbf i}+(x sinz) \, \hat{ \mathbf j}+(xy cosz) \, \hat{ \mathbf k}$ is conservative.

4. The Vector field $\vecs{F}(x,y,z)=y \, \hat{ \mathbf i}+(x+z) \, \hat{ \mathbf j}−y \, \hat{ \mathbf k}$ is conservative.

Answer

1. T, 3. T

Exercise $\PageIndex{2}$: Line integral over vector field

5. Justify the Fundamental Theorem of Line Integrals for $\int _C \vecs{F} · \vecs{dr}$ in the case when $\vecs{F}(x,y)=(2x+2y) \, \hat{ \mathbf i}+(2x+2y) \, \hat{ \mathbf j}$ and $C$ is a portion of the positively oriented circle $x^2+y^2=25$ from $(5, 0)$ to $(3, 4).$

Answer

$\int _C \vecs{F} · \vecs{dr}=24$

6. [T] Find $\int _C \vecs{F} · \vecs{dr},$ where  $\vecs{F}(x,y)=(ye^{xy}+ \cos(x)) \, \hat{ \mathbf i} + (xe^{xy}+\dfrac{1}{y^2+1}) \, \hat{ \mathbf j}$ and $C$ is a portion of curve

$y=sinx$ from $x=0$ to $x=\dfrac{π}{2}$.

7. [T] Evaluate line integral $\int _C \vecs{F} · \vecs{dr}$, where $\vecs{F}(x,y)=(e^xsiny−y) \, \hat{ \mathbf i}+(e^xcosy−x−2)\, \hat{ \mathbf j}$, and $C$ is the path given by

$r(t)=(t^3sin\dfrac{πt}{2}) \, \hat{ \mathbf i}−(\dfrac{π}{2}cos(\dfrac{πt}{2}+\dfrac{π}{2})) \, \hat{ \mathbf j}$ for $0≤t≤1$.

 

Answer

$e-\dfrac{3 \pi}{2}$ 

 

Exercise $\PageIndex{3}$

For the following exercises, determine whether the vector field is conservative and, if it is, find the potential function.

8. $\vecs{F}(x,y)=2xy^3 \, \hat{ \mathbf i} +3y^2x^2 \, \hat{ \mathbf j}$

9. $\vecs{F}(x,y)=(−y+e^xsiny) \, \hat{ \mathbf i} +[(x+2)e^xcosy] \, \hat{ \mathbf j}$

Answer

Not conservative

10. $\vecs{F}(x,y)=(e^{2x}siny) \, \hat{ \mathbf i} +[e^{2x}cosy] \, \hat{ \mathbf j}$

11. $\vecs{F}(x,y)=(6x+5y) \, \hat{ \mathbf i} +(5x+4y) \, \hat{ \mathbf j}$

Answer

Conservative, $\vecs{F}(x,y)=3x^2+5xy+2y^2$

12. $\vecs{F}(x,y)=[2xcos(y)−ycos(x)] \, \hat{ \mathbf i} +[−x^2sin(y)−sin(x)] \, \hat{ \mathbf j}$

13. $\vecs{F}(x,y)=[ye^x+sin(y)] \, \hat{ \mathbf i} +[e^x+xcos(y)] \, \hat{ \mathbf j}$

Answer

Conservative, $\vecs{F}(x,y)=ye^x+xsin(y)$

Exercise $\PageIndex{4}$

For the following exercises, evaluate the line integrals using the Fundamental Theorem of Line Integrals.

14. $\int _C(y \, \hat{ \mathbf i} +x \, \hat{ \mathbf j} )·dr,$ where$C$ is any path from $(0, 0)$ to $(2, 4)$

15. $\int _C(2ydx+2xdy),$ where $C$ is the line segment from (0, 0) to (4, 4)

Answer

$\int _C(2ydx+2xdy)=32$

16. [T] $\int _C[arctan\dfrac{y}{x}−\dfrac{xy}{x^2+y^2}]dx+[\dfrac{x^2}{x^2+y^2}+e^{−y}(1−y)]dy$, where $C$ is any smooth curve from $(1, 1)$ to $(−1,2)$

17. Find the conservative vector field for the potential function

${f}(x,y)=5x^2+3xy+10y^2.$

 

Answer

$\vecs{F}(x,y)=(10x+3y)i+(3x+10y)j$

Exercise $\PageIndex{5}$

For the following exercises, determine whether the vector field is conservative and, if so, find a potential function.

18. $\vecs{F}(x,y)=(12xy) \, \hat{ \mathbf i} +6(x^2+y^2) \, \hat{ \mathbf j}$

19. $\vecs{F}(x,y)=(e^xcosy) \, \hat{ \mathbf i} +6(e^xsiny) \, \hat{ \mathbf j}$

Answer

F is not conservative.

20. $\vecs{F}(x,y)=(2xye^{x^2y}) \, \hat{ \mathbf i} +6(x^2e^{x^2y}) \, \hat{ \mathbf j}$

21. $F(x,y,z)=(ye^z) \, \hat{ \mathbf i} +(xe^z) \, \hat{ \mathbf j} +(xye^z) \, \hat{ \mathbf k}$

Answer

F is conservative and a potential function is $f(x,y,z)=xye^z$.

22. $F(x,y,z)=(siny) \, \hat{ \mathbf i} −(xcosy) \, \hat{ \mathbf j} + \, \hat{ \mathbf k}$

23. $F(x,y,z)=(\dfrac{1}{y}) \, \hat{ \mathbf i} +(\dfrac{x}{y^2}) \, \hat{ \mathbf j} +(2z−1) \, \hat{ \mathbf k}$

Answer

F is conservative and a potential function is $f(x,y,z)=z^2-z-\dfrac{x}{y}.$

24. $F(x,y,z)=3z^2 \, \hat{ \mathbf i} −cosy \, \hat{ \mathbf j} +2xz \, \hat{ \mathbf k}$

25. $F(x,y,z)=(2xy) \, \hat{ \mathbf i} +(x^2+2yz) \, \hat{ \mathbf j} +y^2 \, \hat{ \mathbf k}$

Answer

F is conservative and a potential function is $f(x,y,z)=x^2y+y^2z.$

Exercise $\PageIndex{6}$

For the following exercises, determine whether the given vector field is conservative and find a potential function.

26. $\vecs{F}(x,y)=(e^xcosy) \, \hat{ \mathbf i} +6(e^xsiny) \, \hat{ \mathbf j}$

27. $\vecs{F}(x,y)=(2xye^{x^2y}) \, \hat{ \mathbf i} +6(x^2e^{x^2y}) \, \hat{ \mathbf j}$

Answer

$\vecs{F}$ is conservative and a potential function is $f(x,y)=e^{x^2y}$

Exercise $\PageIndex{7}$

For the following exercises, evaluate the integral using the Fundamental Theorem of Line Integrals.

28. Evaluate $\int _C \vecs{∇f} · \vecs{dr}$, where $f(x,y,z)=cos(πx)+sin(πy)−xyz$ and $C$ is any path that starts at $(1,12,2)$ and ends at $(2,1,−1)$.

29. [T] Evaluate $\int _C \vecs{∇f} · \vecs{dr}$, where $f(x,y)=xy+e^x$ and $C$ is a straight line from $(0,0)$ to $(2,1)$.

Answer

Solution: $\int _C \vecs{F} · \vecs{dr}=e^2+1$

30. [T] Evaluate $\int _C \vecs{∇f} · \vecs{dr},$ where $f(x,y)=x^2y−x$ and $C$ is any path in a plane from (1, 2) to (3, 2).

31. Evaluate $\int _C \vecs{∇f} · \vecs{dr},$ where $f(x,y,z)=xyz^2−yz$ and $C$ has initial point (1, 2,3) and terminal point (3, 5,1).

Answer

$\int _C \vecs{F} · \vecs{dr}=-2$

Exercise $\PageIndex{8}$

For the following exercises, let $\vecs{F}(x,y)=2xy^2 \, \hat{ \mathbf i} +(2yx^2+2y)\, \hat{ \mathbf j}$ and $G(x,y)=(y+x)\, \hat{ \mathbf i}+(y−x)\, \hat{ \mathbf j}$, and let $C_1$ be the curve consisting of the circle of radius 2, centered at the origin and oriented counterclockwise, and $C_2$ be the curve consisting of a line segment from (0, 0) to (1, 1) followed by a line segment from (1, 1) to (3, 1).

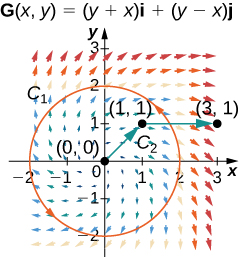
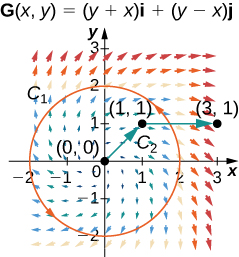
32. Calculate the line integral of F over $C_1$.

33. Calculate the line integral of G over $C_1$.

Answer

Solution: $∮_{C_1}\bf{G}· \bf{dr}=−8π$

34. Calculate the line integral of F over $C_2$.

35. Calculate the line integral of G over $C_2$.

Answer

Solution: $∮_{C_2}F·dr=7$

36. [T] Let $F(x,y,z)=x^2 \, \hat{ \mathbf i} +zsin(yz)j+ysin(yz)k$. Calculate $∮_CF·dr$, where $C$ is a path from $A=(0,0,1)$ to $B=(3,1,2)$.

37. [T] Find line integral $∮_CF·dr$ of vector field $F(x,y,z)=3x^2z \, \hat{ \mathbf i} +z^2\, \hat{ \mathbf j}+(x^3+2yz)\, \hat{ \mathbf k}$ along curve $C$ parameterized by $r(t)=(\dfrac{lnt}{ln2}) \, \hat{ \mathbf i} +t^{3/2}\, \hat{ \mathbf j}+tcos(πt) \, \hat{ \mathbf k},1≤t≤4.$

Answer

Solution: $\int _C \vecs{F} · \vecs{dr}=150$

Exercise $\PageIndex{9}$

For the following exercises, show that the following vector fields are conservative. Calculate $\int _C \vecs{F} · \vecs{dr}$ for the given curve.

38. $\vecs{F}=(xy^2+3x^2y)\, \hat{ \mathbf i}+(x+y)x^2\, \hat{ \mathbf j}$; $C$ is the curve consisting of line segments from (1,1)to (0,2) to (3,0).

39. $\vecs{F}=\dfrac{2x}{y^2+1}\, \hat{ \mathbf i}−\dfrac{2y(x^2+1)}{(y^2+1)^2}\, \hat{ \mathbf j}$; $C$ is parameterized by $x=t^3−1,y=t^6−t,0≤t≤1.$

Answer

Solution: $\int _C \vecs{F} · \vecs{dr}=−1$

40. [T] $\vecs{F}=[cos(xy^2)−xy^2sin(xy^2)]\, \hat{ \mathbf i}−2x^2ysin(xy^2)\, \hat{ \mathbf j}$; $C$ is curve $(e^t,e^{t+1}),−1≤t≤0$.

Exercise $\PageIndex{10}$

41. The mass of Earth is approximately $6×10^{27}g$, and that of the Sun is 330,000 times as much. The gravitational constant is $6.7×10^{−8}cm^3/s^2·g$. The distance of Earth from the Sun is about $1.5×10^{12}cm$. Compute, approximately, the work necessary to increase the distance of Earth from the Sun by 1 cm.

Solution: $4×10^{31}erg$

42. [T] Let $\vecs{F}=(x,y,z)=(e^xsiny)\, \hat{ \mathbf i}+(e^xcosy)\, \hat{ \mathbf j}+z^2\, \hat{ \mathbf k}$. Evaluate the integral $\int _C \vecs{F}·\vecs{ds}$,where $C(t)=(\sqrt{t},t^3,e^{\sqrt{t}}),0≤t≤1.$

43. [T] Let $c:[1,2]→ℝ^2$ be given by $x=e^{t−1},y=sin(\dfrac{π}{t})$. Use a computer to compute the integral $\int _CF·ds=\int _C2xcosydx−x^2sinydy$, where $\vecs{F}=(2xcosy)i−(x^2siny)j.$

Answer

Solution: $\int _CF·ds=0.4687$

 

44. [T] Use a computer algebra system to find the mass of a wire that lies along curve $r(t)=(t^2−1)\, \hat{ \mathbf j}+2t\, \hat{ \mathbf k},0≤t≤1$, if the density is $\dfrac{3}{2}t$.

45. Find the circulation and flux of field $\vecs{F}=−y\, \hat{ \mathbf i}+x\, \hat{ \mathbf k}$ around and across the closed semicircular path that consists of semicircular arch $r_1(t)=(acost)\, \hat{ \mathbf i}+(asint)\, \hat{ \mathbf j},0≤t≤π$, followed by line segment $r_2(t)=t\, \hat{ \mathbf i},−a≤t≤a.$

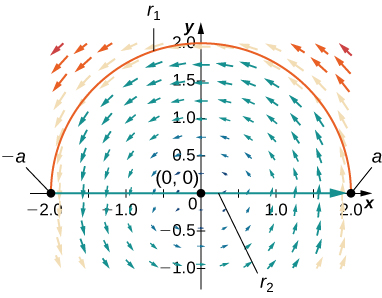
Answer

Solution: $circulation=πa^2$ and $flux=0$

 

46. Compute $\int _C cosxcosydx−sinxsinydy,$ where $C(t)=(t,t^2),0≤t≤1.$

47. Complete the proof of Note by showing that $f_y=Q(x,y).$