1.1E: Exercises

Exercise $\PageIndex{1}$

In the following exercises, state whether each statement is true, or give an example to show that it is false.

1. If $\displaystyle \sum_{n=1}^∞a_nx^n$ converges, then $\displaystyle a_nx^n→0$ as $\displaystyle n→∞.$

Answer

True. If a series converges then its terms tend to zero.

2. $\displaystyle \sum_{n=1}^∞a_nx^n$ converges at $\displaystyle x=0$ for any real numbers $\displaystyle a_n$.

3. Given any sequence $\displaystyle a_n$, there is always some $\displaystyle R>0$, possibly very small, such that $\displaystyle \sum_{n=1}^∞a_nx^n$ converges on $\displaystyle (−R,R)$.

Answer

False. It would imply that $\displaystyle a_nx^n→0$ for $\displaystyle |x|<R$. If $\displaystyle a_n=n^n$, then $\displaystyle a_nx^n=(nx)^n$ does not tend to zero for any $\displaystyle x≠0$.

4. If $\displaystyle \sum_{n=1}^∞a_nx^n$ has radius of convergence $\displaystyle R>0$ and if $\displaystyle |b_n|≤|a_n|$ for all $\displaystyle n$, then the radius of convergence of $\displaystyle \sum_{n=1}^∞b_nx^n$ is greater than or equal to $\displaystyle R$

Exercise $\PageIndex{2}$

1. Suppose that $\displaystyle \sum_{n=0}^∞a_n(x−3)^n$ converges at $\displaystyle x=6$. At which of the following points must the series also converge? Use the fact that if $\displaystyle \sum a_n(x−c)^n$ converges at $\displaystyle x$, then it converges at any point closer to $\displaystyle c$ than $\displaystyle x$.

a. $\displaystyle x=1$

b. $\displaystyle x=2$

c. $\displaystyle x=3$

d. $\displaystyle x=0$

e. $\displaystyle x=5.99$

f. $\displaystyle x=0.000001$

Answer

It must converge on $\displaystyle (0,6]$ and hence at: a. $\displaystyle x=1$; b. $\displaystyle x=2$; c. $\displaystyle x=3$; d. $\displaystyle x=0$; e. $\displaystyle x=5.99$; and f. $\displaystyle x=0.000001$.

2. Suppose that $\displaystyle \sum_{n=0}^∞a_n(x+1)^n$ converges at $\displaystyle x=−2$. At which of the following points must the series also converge? Use the fact that if $\displaystyle \sum a_n(x−c)^n$ converges at $\displaystyle x$, then it converges at any point closer to $\displaystyle c$ than $\displaystyle x$.

a. $\displaystyle x=2$

b. $\displaystyle x=−1$

c. $\displaystyle x=−3$

d. $\displaystyle x=0$

e. $\displaystyle x=0.99$

f. $\displaystyle x=0.000001$

Exercise $\PageIndex{3}$

In the following exercises, suppose that $\displaystyle ∣\frac{a_{n+1}}{a_n}∣→1$ as $\displaystyle n→∞.$ Find the radius of convergence for each series.

1. $\displaystyle \sum_{n=0}^∞a_n2^nx^n$

Answer

$\displaystyle ∣\frac{a_{n+1}2^{n+1}x^{n+1}}{a_n2^nx^n}∣ =2|x|∣ \frac{a_{n+1}}{a_n}∣→2|x|$ so $\displaystyle R=\frac{1}{2}$

2. $\displaystyle \sum_{n=0}^∞\frac{a_nx^n}{2^n}$

Answer

$\displaystyle|\frac{a_{n+1}x^{n+1}}{2^{n+1}} \frac{2^n}{a_nx^n}| = \frac{|x|}{2}| \frac{a_{n+1}}{a_n}∣→\frac{|x|}{2}$ so $R=2$

3. $\displaystyle \sum_{n=0}^∞\frac{a_nπ^nx^n}{e^n}$

Answer

$\displaystyle ∣\frac{a_{n+1}(\frac{π}{e})^{n+1}x^{n+1}}{a_n(\frac{π}{e})^nx^n}∣ =\frac{π|x|}{e}∣\frac{a_{n+1}}{a_n}∣→\frac{π|x|}{e}$ so $\displaystyle R=\frac{e}{π}$

4. $\displaystyle \sum_{n=0}^∞\frac{a_n(−1)^nx^n}{10^n}$

Answer

$\displaystyle|\frac{a_{n+1}(-1)^{n+1}x^{n+1}}{10^{n+1}} \frac{10^n}{a_n(-1)^nx^n}| = \frac{|x|}{10}| \frac{a_{n+1}}{a_n}∣→\frac{|x|}{10}$ so $R=10$

5. $\displaystyle \sum_{n=0}^∞a_n(−1)^nx^{2n}$

Answer

$\displaystyle ∣\frac{a_{n+1}(−1)^{n+1}x^{2n+2}}{a_n(−1)^nx^{2n}}∣ =∣x^2∣∣\frac{a_{n+1}}{a_n}∣→∣x^2∣$ so $\displaystyle R=1$

6. $\displaystyle \sum_{n=0}^∞a_n(−4)^nx^{2n}$

Answer

$\displaystyle ∣\frac{a_{n+1}(-4)^{n+1}x^{2(n+1)}}{a_n(-4)^nx^{2n}}∣ =4|x^2|∣ \frac{a_{n+1}}{a_n}∣→4|x^2|$ so $\displaystyle R=\frac{1}{2}$

Exercise $\PageIndex{4}$

In the following exercises, find the radius of convergence $\displaystyle R$ and interval of convergence for $\displaystyle \sum a_nx^n$ with the given coefficients $\displaystyle a_n$.

1. $\displaystyle \sum_{n=1}^∞\frac{(2x)^n}{n}$

Answer

$\displaystyle a_n=\frac{2^n}{n}$ so $\displaystyle \frac{a_{n+1}x}{a_n}→2x$. so $\displaystyle R=\frac{1}{2}$. When $\displaystyle x=\frac{1}{2}$ the series is harmonic and diverges. When $\displaystyle x=−\frac{1}{2}$ the series is alternating harmonic and converges. The interval of convergence is $\displaystyle I=[−\frac{1}{2},\frac{1}{2})$.

2. $\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\sqrt{n}}$

Answer

R=1

Interval of convergence (-1,1)

3. $\displaystyle \sum_{n=1}^∞\frac{nx^n}{2^n}$

Answer

$\displaystyle a_n=\frac{n}{2^n}$ so $\displaystyle \frac{a_{n+1}x}{a_n}→\frac{x}{2}$ so $\displaystyle R=2$. When $\displaystyle x=±2$ the series diverges by the divergence test. The interval of convergence is $\displaystyle I=(−2,2)$.

4. $\displaystyle \sum_{n=1}^∞\frac{nx^n}{e^n}$

5. $\displaystyle \sum_{n=1}^∞\frac{n^2x^n}{2^n}$

Answer

$\displaystyle a_n=\frac{n^2}{2^n}$ so $\displaystyle R=2$. When $\displaystyle x=±2$ the series diverges by the divergence test. The interval of convergence is $\displaystyle I=(−2,2).$

6. $\displaystyle \sum_{k=1}^∞\frac{k^ex^k}{e^k}$

7. $\displaystyle \sum_{k=1}^∞\frac{π^kx^k}{k^π}$

Answer

$\displaystyle a_k=\frac{π^k}{k^π}$ so $\displaystyle R=\frac{1}{π}$. When $\displaystyle x=±\frac{1}{π}$ the series is an absolutely convergent p-series. The interval of convergence is $\displaystyle I=[−\frac{1}{π},\frac{1}{π}].$

8. $\displaystyle \sum_{n=1}^∞\frac{x^n}{n!}$

9. $\displaystyle \sum_{n=1}^∞\frac{10^nx^n}{n!}$

Answer

$\displaystyle a_n=\frac{10^n}{n!},\frac{a_{n+1}x}{a_n}=\frac{10x}{n+1}→0<1$ so the series converges for all $\displaystyle x$ by the ratio test and $\displaystyle I=(−∞,∞)$.

10. $\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{ln(2n)}$

Exercise $\PageIndex{5}$

In the following exercises, find the radius of convergence of each series.

1. $\displaystyle \sum_{k=1}^∞\frac{(k!)^2x^k}{(2k)!}$

Answer

$\displaystyle a_k=\frac{(k!)^2}{(2k)!}$ so $\displaystyle \frac{a_{k+1}}{a_k}=\frac{(k+1)^2}{(2k+2)(2k+1)}→\frac{1}{4}$ so $\displaystyle R=4$

2. $\displaystyle \sum_{n=1}^∞\frac{(2n)!x^n}{n^{2n}}$

3. $\displaystyle \sum_{k=1}^∞\frac{k!}{1⋅3⋅5⋯(2k−1)}x^k$

Answer

$\displaystyle a_k=\frac{k!}{1⋅3⋅5⋯(2k−1)}$ so $\displaystyle \frac{a_{k+1}}{a_k}=\frac{k+1}{2k+1}→\frac{1}{2}$ so $\displaystyle R=2$

4. $\displaystyle \sum_{k=1}^∞\frac{2⋅4⋅6⋯2k}{(2k)!}x^k$

5. $\displaystyle \sum_{n=1}^∞\frac{x^n}{(^{2n}_n)}$ where $\displaystyle (^n_k)=\frac{n!}{k!(n−k)!}$

Answer

$\displaystyle a_n=\frac{1}{(^{2n}_n)}$ so $\displaystyle \frac{a_{n+1}}{a_n}=\frac{((n+1)!)^2}{(2n+2)!}\frac{2n!}{(n!)^2}=\frac{(n+1)^2}{(2n+2)(2n+1)}→\frac{1}{4}$ so $\displaystyle R=4$

6. $\displaystyle \sum_{n=1}^∞sin^2nx^n$

Exercise $\PageIndex{6}$

In the following exercises, use the ratio test to determine the radius of convergence of each series.

1. $\displaystyle \sum_{n=1}^∞\frac{(n!)^3}{(3n)!}x^n$

Answer

$\displaystyle \frac{a_{n+1}}{a_n}=\frac{(n+1)^3}{(3n+3)(3n+2)(3n+1)}→\frac{1}{27}$ so $\displaystyle R=27$

2. $\displaystyle \sum_{n=1}^∞\frac{2^{3n}(n!)^3}{(3n)!}x^n$

3. $\displaystyle \sum_{n=1}^∞\frac{n!}{n^n}x^n$

Answer

$\displaystyle a_n=\frac{n!}{n^n}$ so $\displaystyle \frac{a_{n+1}}{a_n}=\frac{(n+1)!}{n!}\frac{n^n}{(n+1)^{n+1}}=(\frac{n}{n+1})^n→\frac{1}{e}$ so $\displaystyle R=e$

4. $\displaystyle \sum_{n=1}^∞\frac{(2n)!}{n^{2n}}x^n$

Exercise $\PageIndex{7}$

In the following exercises, given that $\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n$ with convergence in $\displaystyle (−1,1)$, find the power series for each function with the given center a, and identify its interval of convergence.

1. $\displaystyle f(x)=\frac{1}{x};a=1$ (Hint: $\displaystyle \frac{1}{x}=\frac{1}{1−(1−x)})$

Answer

$\displaystyle f(x)=\sum_{n=0}^∞(1−x)^n$ on $\displaystyle I=(0,2)$

2. $\displaystyle f(x)=\frac{1}{1−x^2};a=0$

3. $\displaystyle f(x)=\frac{x}{1−x^2};a=0$

Answer

$\displaystyle \sum_{n=0}^∞x^{2n+1}$ on $\displaystyle I=(−1,1)$

4. $\displaystyle f(x)=\frac{1}{1+x^2};a=0$

5. $\displaystyle f(x)=\frac{x^2}{1+x^2};a=0$

Answer

$\displaystyle \sum_{n=0}^∞(−1)^nx^{2n+2}$ on $\displaystyle I=(−1,1)$

6. $\displaystyle f(x)=\frac{1}{2−x};a=1$

7. $\displaystyle f(x)=\frac{1}{1−2x};a=0.$

Answer

$\displaystyle \sum_{n=0}^∞2^nx^n$ on $\displaystyle (−\frac{1}{2},\frac{1}{2})$

8. $\displaystyle f(x)=\frac{1}{1−4x^2};a=0$

9. $\displaystyle f(x)=\frac{x^2}{1−4x^2};a=0$

Answer

$\displaystyle \sum_{n=0}^∞4^nx^{2n+2}$ on $\displaystyle (−\frac{1}{2},\frac{1}{2})$

10. $\displaystyle f(x)=\frac{x^2}{5−4x+x^2};a=2$

Exercise $\PageIndex{8}$

Use the next exercise to find the radius of convergence of the given series in the subsequent exercises.

1. Explain why, if $\displaystyle |a_n|^{1/n}→r>0,$ then $\displaystyle |a_nx^n|^{1/n}→|x|r<1$ whenever $\displaystyle |x|<\frac{1}{r}$ and, therefore, the radius of convergence of $\displaystyle \sum_{n=1}^∞a_nx^n$ is $\displaystyle R=\frac{1}{r}$.

Answer

$\displaystyle |a_nx^n|^{1/n}=|a_n|^{1/n}|x|→|x|r$ as $\displaystyle n→∞$ and $\displaystyle |x|r<1$ when $\displaystyle |x|<\frac{1}{r}$. Therefore, $\displaystyle \sum_{n=1}^∞a_nx^n$ converges when $\displaystyle |x|<\frac{1}{r}$ by the nth root test.

2. $\displaystyle \sum_{n=1}^∞\frac{x^n}{n^n}$

3. $\displaystyle \sum_{k=1}^∞(\frac{k−1}{2k+3})^kx^k$

Answer

$\displaystyle a_k=(\frac{k−1}{2k+3})^k$ so $\displaystyle (a_k)^{1/k}→\frac{1}{2}<1$ so $\displaystyle R=2$

4. $\displaystyle \sum_{k=1}^∞(\frac{2k^2−1}{k^2+3})^kx^k$

5. $\displaystyle \sum_{n=1}^∞a_n=(n^{1/n}−1)^nx^n$

Answer

$\displaystyle a_n=(n^{1/n}−1)^n$ so $\displaystyle (a_n)^{1/n}→0$ so $\displaystyle R=∞$

6. Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ such that $\displaystyle a_n=0$ if $\displaystyle n$ is even. Explain why $\displaystyle p(x)=p(−x).$

7. Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ such that $\displaystyle a_n=0$ if $\displaystyle n$ is odd. Explain why $\displaystyle p(x)=−p(−x).$

Answer

We can rewrite $\displaystyle p(x)=\sum_{n=0}^∞a_{2n+1}x^{2n+1}$ and $\displaystyle p(x)=p(−x)$ since $\displaystyle x^{2n+1}=−(−x)^{2n+1}$.

8. Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ converges on $\displaystyle (−1,1]$. Find the interval of convergence of $\displaystyle p(Ax)$.

9. Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ converges on $\displaystyle (−1,1]$. Find the interval of convergence of $\displaystyle p(2x−1)$.

Answer

If $\displaystyle x∈[0,1],$ then $\displaystyle y=2x−1∈[−1,1]$ so $\displaystyle p(2x−1)=p(y)=\sum_{n=0}^∞a_ny^n$ converges.

Exercise $\PageIndex{9}$

In the following exercises, suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ satisfies $\displaystyle \lim_{n→∞}\frac{a_{n+1}}{a_n}=1$ where $\displaystyle a_n≥0$ for each $\displaystyle n$. State whether each series converges on the full interval $\displaystyle (−1,1)$, or if there is not enough information to draw a conclusion. Use the comparison test when appropriate.

1. $\displaystyle \sum_{n=0}^∞a_nx^{2n}$

2. $\displaystyle \sum_{n=0}^∞a_{2n}x^{2n}$

Answer

Converges on $\displaystyle (−1,1)$ by the ratio test

3. $\displaystyle \sum_{n=0}^∞a_{2n}x^n$ (Hint:$\displaystyle x=±\sqrt{x^2}$)

4. $\displaystyle \sum_{n=0}^∞a_{n^2}x^{n^2}$ (Hint: Let $\displaystyle b_k=a_k$ if $\displaystyle k=n^2$ for some $\displaystyle n$, otherwise $\displaystyle b_k=0$.

Answer

Consider the series $\displaystyle \sum b_kx^k$ where $\displaystyle b_k=a_k$ if $\displaystyle k=n^2$ and $\displaystyle b_k=0$ otherwise. Then $\displaystyle b_k≤a_k$ and so the series converges on $\displaystyle (−1,1)$ by the comparison test.

5. Suppose that $\displaystyle p(x)$ is a polynomial of degree $\displaystyle N$. Find the radius and interval of convergence of $\displaystyle \sum_{n=1}^∞p(n)x^n$.

Exercise $\PageIndex{10}$

1. Plot the graphs of $\displaystyle \frac{1}{1−x}$ and of the partial sums $\displaystyle S_N=\sum_{n=0}^Nx^n$ for $\displaystyle n=10,20,30$ on the interval $\displaystyle [−0.99,0.99]$. Comment on the approximation of $\displaystyle \frac{1}{1−x}$ by $\displaystyle S_N$ near $\displaystyle x=−1$ and near $\displaystyle x=1$ as $\displaystyle N$ increases.

Answer

The approximation is more accurate near $\displaystyle x=−1$. The partial sums follow $\displaystyle \frac{1}{1−x}$ more closely as $\displaystyle N$ increases but are never accurate near $\displaystyle x=1$ since the series diverges there.

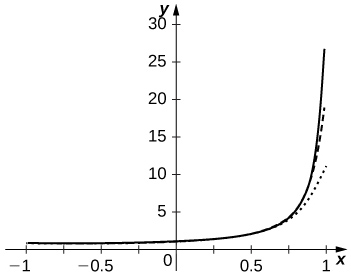
2. Plot the graphs of $\displaystyle −ln(1−x)$ and of the partial sums $\displaystyle S_N=\sum_{n=1}^N\frac{x^n}{n}$ for $\displaystyle n=10,50,100$ on the interval $\displaystyle [−0.99,0.99]$. Comment on the behavior of the sums near $\displaystyle x=−1$ and near $\displaystyle x=1$ as $\displaystyle N$ increases.

3. Plot the graphs of the partial sums $\displaystyle S_n=\sum_{n=1}^N\frac{x^n}{n^2}$ for $\displaystyle n=10,50,100$ on the interval $\displaystyle [−0.99,0.99]$. Comment on the behavior of the sums near $\displaystyle x=−1$ and near $\displaystyle x=1$ as $\displaystyle N$ increases.

Answer

The approximation appears to stabilize quickly near both $\displaystyle x=±1$.

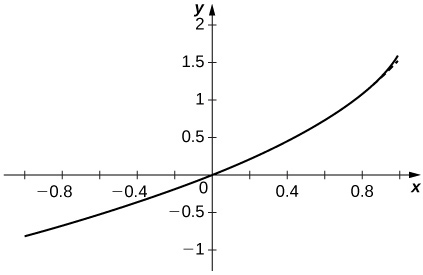
4. Plot the graphs of the partial sums $\displaystyle S_N=\sum_{n=1}^Nsinnx^n$ for $\displaystyle n=10,50,100$ on the interval $\displaystyle [−0.99,0.99]$. Comment on the behavior of the sums near $\displaystyle x=−1$ and near $\displaystyle x=1$ as $\displaystyle N$ increases.

5. Plot the graphs of the partial sums $\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n+1}}{(2n+1)!}$ for $\displaystyle n=3,5,10$ on the interval $\displaystyle [−2π,2π]$. Comment on how these plots approximate $\displaystyle sinx$ as $\displaystyle N$ increases.

Answer

The polynomial curves have roots close to those of $\displaystyle sinx$ up to their degree and then the polynomials diverge from $\displaystyle sinx$.

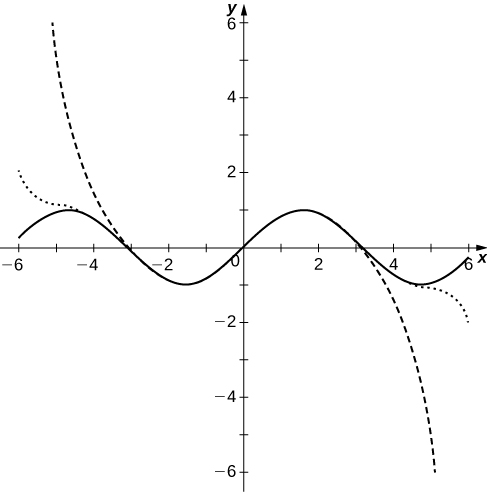
6. Plot the graphs of the partial sums $\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n}}{(2n)!}$ for $\displaystyle n=3 ,5,10$ on the interval $\displaystyle [−2π,2π]$. Comment on how these plots approximate $\displaystyle cosx$ as $\displaystyle N$ increases.