4.2: Further Topics in Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
This section serves as a watershed for functions which are combinations of polynomial, and more generally, rational functions, with the operations of radicals. It is business of Calculus to discuss these functions in all the detail they demand so our aim in this section is to help shore up the requisite skills needed so that the reader can answer Calculus’s call when the time comes. We briefly recall the definition and some of the basic properties of radicals from Intermediate Algebra.1
Let x be a real number and n a natural number.a If n is odd, the principal nth root of x, denoted n√x is the unique real number satisfying
(n√x)n=x.
If n is even, n√x is defined similarlyb provided x≥0 and n√x≥0. The index is the number n and the radicand is the number x. For n=2, we write √x instead of 2√x.
a Recall this means n=1,2,3,. . ..
b Recall both x=−2 and x=2 satisfy x4=16, but 4√16=2, not −2.
It is worth remarking that, in light of Section 5.2, we could define f(x)=n√x functionally as the inverse of g(x)=xn with the stipulation that when n is even, the domain of g is restricted to [0,∞). From what we know about g(x)=xn from Section 3.1 along with Theorem 5.3, we can produce the graphs of f(x)=n√x by reflecting the graphs of g(x)=xn across the line y=x. Below are the graphs of y=√x, y=4√x and y=6√x. The point (0,0) is indicated as a reference. The axes are hidden so we can see the vertical steepening near x=0 and the horizontal flattening as x→∞.
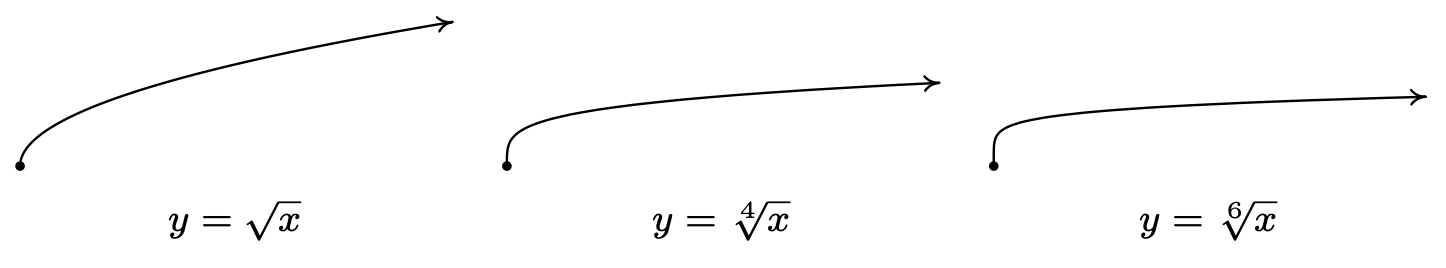
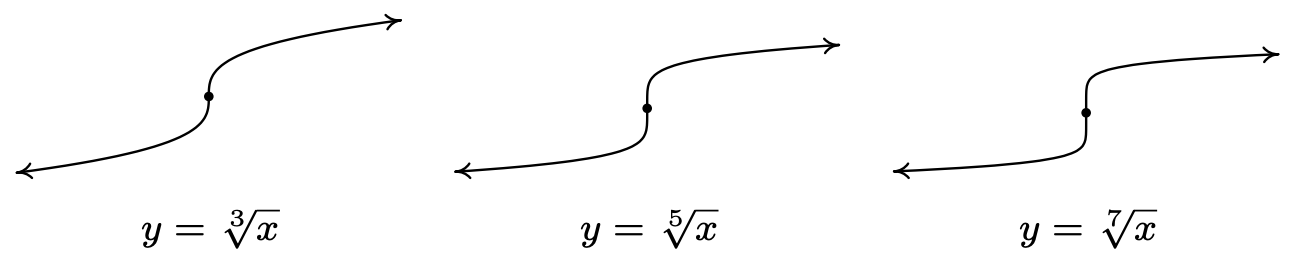
The odd-indexed radical functions also follow a predictable trend - steepening near x=0 and flattening as x→±∞. In the exercises, you’ll have a chance to graph some basic radical functions using the techniques presented in Section 1.7.
We have used all of the following properties at some point in the textbook for the case n=2 (the square root), but we list them here in generality for completeness.
Let x and y be real numbers and m and n be natural numbers. If n√x, n√y are real numbers, then
- Product Rule: n√xy=n√xn√y
- Powers of Radicals: n√xm=(n√x)m
- Quotient Rule: n√xy=n√xn√y, provided y≠0.
- If n is odd, n√xn=x; if n is even, n√xn=|x|.
The proof of Theorem 5.6 is based on the definition of the principal roots and properties of exponents. To establish the product rule, consider the following. If n is odd, then by definition n√xy is the unique real number such that (n√xy)n=xy. Given that (n√xn√y)n=(n√x)n(n√y)n=xy, it must be the case that n√xy=n√xn√y. If n is even, then n√xy is the unique non-negative real number such that (n√xy)n=xy. Also note that since n is even, n√x and n√y are also non-negative and hence so is n√xn√y. Proceeding as above, we find that n√xy=n√xn√y. The quotient rule is proved similarly and is left as an exercise. The power rule results from repeated application of the product rule, so long as n√x is a real number to start with.2 The last property is an application of the power rule when n is odd, and the occurrence of the absolute value when n is even is due to the requirement that n√x≥0 in Definition 5.4. For instance, 4√(−2)4=4√16=2=|−2|, not −2. It’s this last property which makes compositions of roots and powers delicate. This is especially true when we use exponential notation for radicals. Recall the following definition.
Let x be a real number, m an integera and n a natural number.
- x1n=n√x and is defined whenever n√x is defined.
- xmn=(n√x)m=n√xm, whenever (n√x)m is defined.
a Recall this means m=0,±1,±2,…
The rational exponents defined in Definition 5.5 behave very similarly to the usual integer exponents from Elementary Algebra with one critical exception. Consider the expression (x2/3)3/2. Applying the usual laws of exponents, we’d be tempted to simplify this as (x2/3)3/2=x23⋅32=x1=x. However, if we substitute x=−1 and apply Definition 5.5, we find (−1)2/3=(3√−1)2=(−1)2=1 so that ((−1)2/3)3/2=13/2=(√1)3=13=1. We see in this case that (x2/3)3/2≠x. If we take the time to rewrite (x2/3)3/2 with radicals, we see
(x2/3)3/2=((3√x)2)3/2=(√(3√x)2)3=(|3√x|)3=|(3√x)3|=|x|
In the play-by-play analysis, we see that when we canceled the 2’s in multiplying 23⋅32, we were, in fact, attempting to cancel a square with a square root. The fact that √x2=|x| and not simply x is the root3 of the trouble. It may amuse the reader to know that (x3/2)2/3=x, and this verification is left as an exercise. The moral of the story is that when simplifying fractional exponents, it’s usually best to rewrite them as radicals.4 The last major property we will state, and leave to Calculus to prove, is that radical functions are continuous on their domains, so the Intermediate Value Theorem, Theorem 3.1, applies. This means that if we take combinations of radical functions with polynomial and rational functions to form what the authors consider the algebraic functions,5 we can make sign diagrams using the procedure set forth in Section 4.2.
Suppose f is an algebraic function.
- Place any values excluded from the domain of f on the number line with an ‘’ above them.
- Find the zeros of f and place them on the number line with the number 0 above them.
- Choose a test value in each of the intervals determined in steps 1 and 2.
- Determine the sign of f(x) for each test value in step 3, and write that sign above the corresponding interval.
Our next example reviews quite a bit of Intermediate Algebra and demonstrates some of the new features of these graphs.
For the following functions, state their domains and create sign diagrams. Check your answer graphically using your calculator
- f(x)=3x3√2−x
- g(x)=√2−4√x+3
- h(x)=3√8xx+1
- k(x)=2x√x2−1
Solution.
- As far as domain is concerned, f(x) has no denominators and no even roots, which means its domain is (−∞,∞). To create the sign diagram, we find the zeros of f.
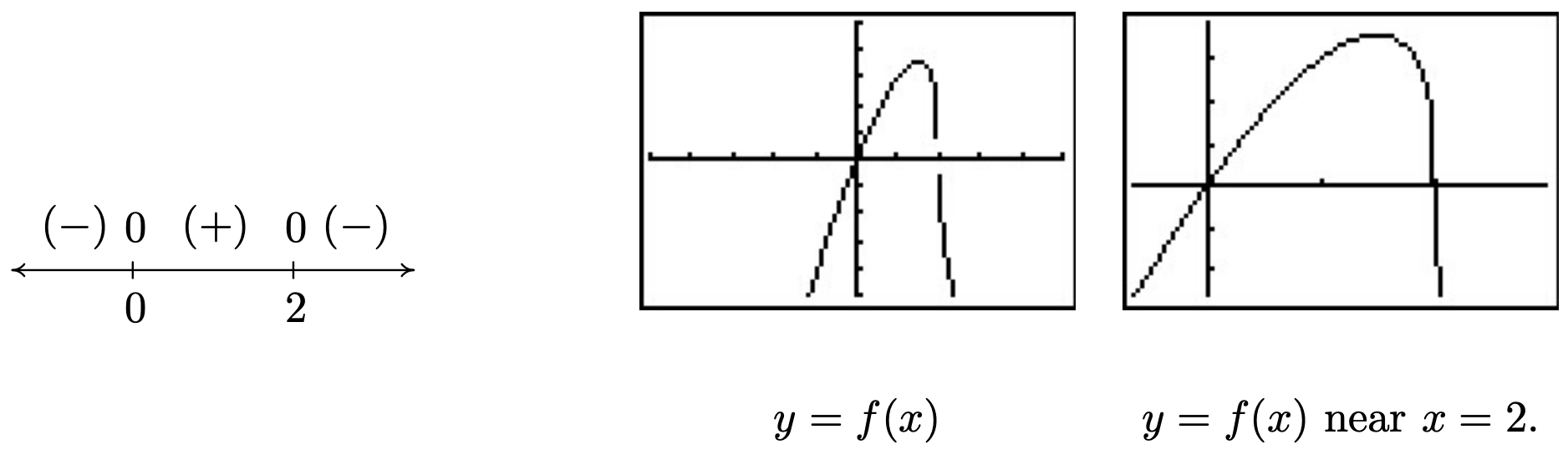
f(x)=03x3√2−x=03x=0or3√2−x=0x=0or(3√2−x)3=03x=0or2−x=0x=0orx=2
The zeros 0 and 2 divide the real number line into three test intervals. The sign diagram and accompanying graph are below. Note that the intervals on which f is (+) correspond to where the graph of f is above the x-axis, and where the graph of f is below the x-axis we have that f is (−). The calculator suggests something mysterious happens near x=2. Zooming in shows the graph becomes nearly vertical there. You’ll have to wait until Calculus to fully understand this phenomenon.
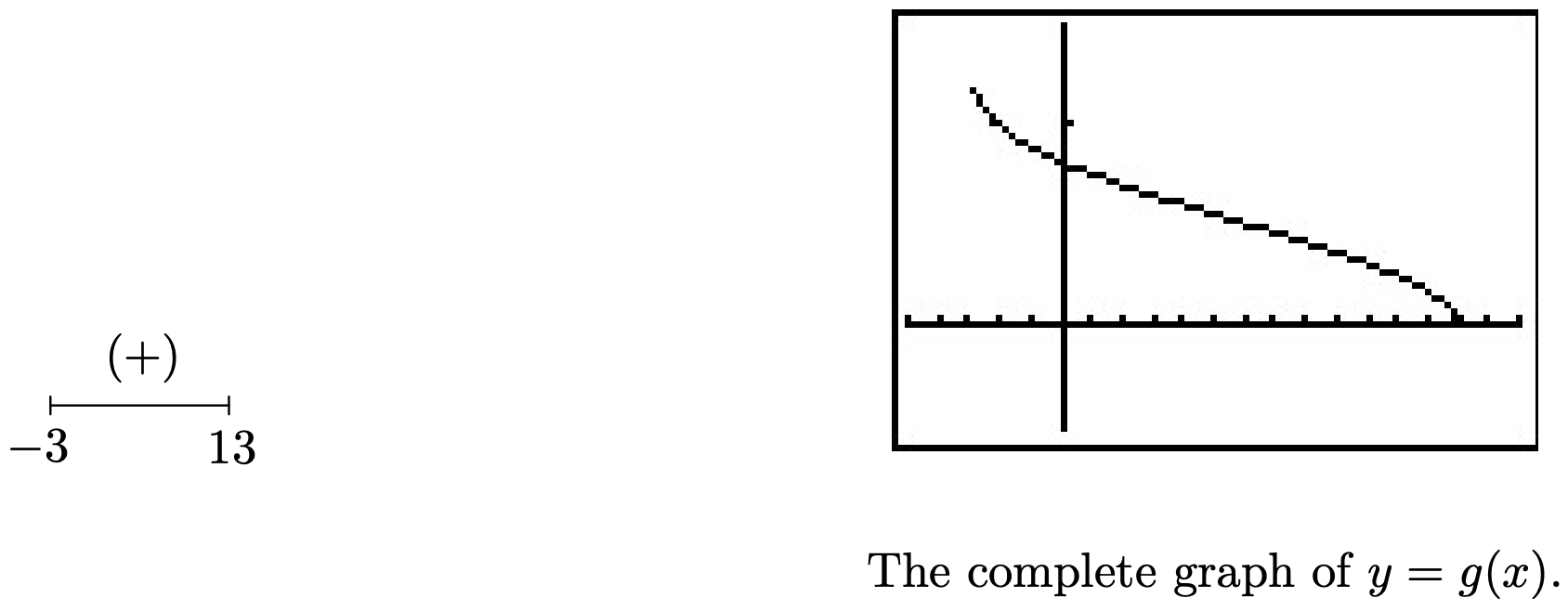
- In g(x)=√2−4√x+3, we have two radicals both of which are even indexed. To satisfy 4√x+3, we require x+3≥0 or x≥−3. To satisfy √2−4√x+3, we need 2−4√x+3≥0. While it may be tempting to write this as 2≥4√x+3 and take both sides to the fourth power, there are times when this technique will produce erroneous results.6 Instead, we solve 2−4√x+3≥0 using a sign diagram. If we let r(x)=2−4√x+3, we know x≥−3, so we concern ourselves with only this portion of the number line. To find the zeros of r we set r(x)=0 and solve 2−4√x+3=0. We get 4√x+3=2 so that (4√x+3)4=24 from which we obtain x+3=16 or x=13. Since we raised both sides of an equation to an even power, we need to check to see if x=13 is an extraneous solution.7 We find x=13 does check since 2−4√x+3=2−4√13+3=2−4√16=2−2=0. Below is our sign diagram for r.
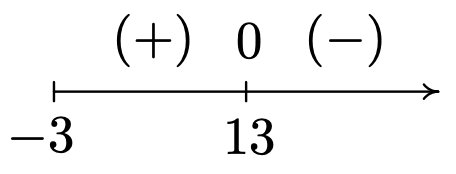
We find 2−4√x+3≥0 on [−3,13] so this is the domain of g. To find a sign diagram for g, we look for the zeros of g. Setting g(x)=0 is equivalent to √2−4√x+3=0. After squaring both sides, we get 2−4√x+3=0, whose solution we have found to be x=13. Since we squared both sides, we double check and find g(13) is, in fact, 0. Our sign diagram and graph of g are below. Since the domain of g is [−3,13], what we have below is not just a portion of the graph of g, but the complete graph. It is always above or on the x-axis, which verifies our sign diagram.
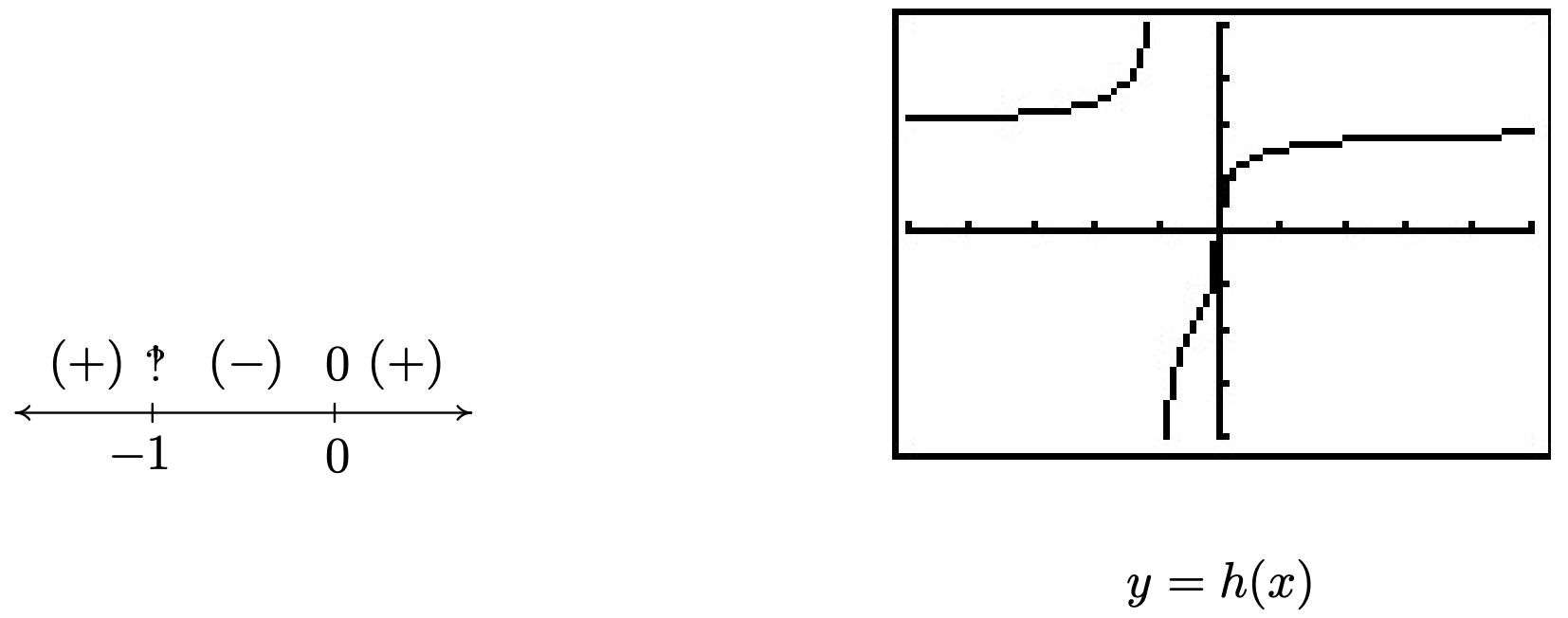
- The radical in h(x) is odd, so our only concern is the denominator. Setting x+1=0 gives x=−1, so our domain is (−∞,−1)∪(−1,∞). To find the zeros of h, we set h(x)=0. To solve 3√8xx+1=0, we cube both sides to get 8xx+1=0. We get 8x=0, or x=0. Below is the resulting sign diagram and corresponding graph. From the graph, it appears as though x=−1 is a vertical asymptote. Carrying out an analysis as x→−1 as in Section 4.2 confirms this. (We leave the details to the reader.) Near x=0, we have a situation similar to x=2 in the graph of f in number 1 above. Finally, it appears as if the graph of h has a horizontal asymptote y=2. Using techniques from Section 4.2, we find as x→±∞, 8xx+1→8. From this, it is hardly surprising that as x→±∞, h(x)=3√8xx+1≈3√8=2.
- To find the domain of k, we have both an even root and a denominator to concern ourselves with. To satisfy the square root, x2−1≥0. Setting r(x)=x2−1, we find the zeros of r to be x=±1, and we find the sign diagram of r to be
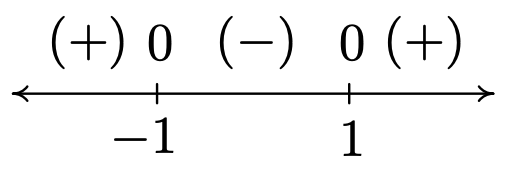
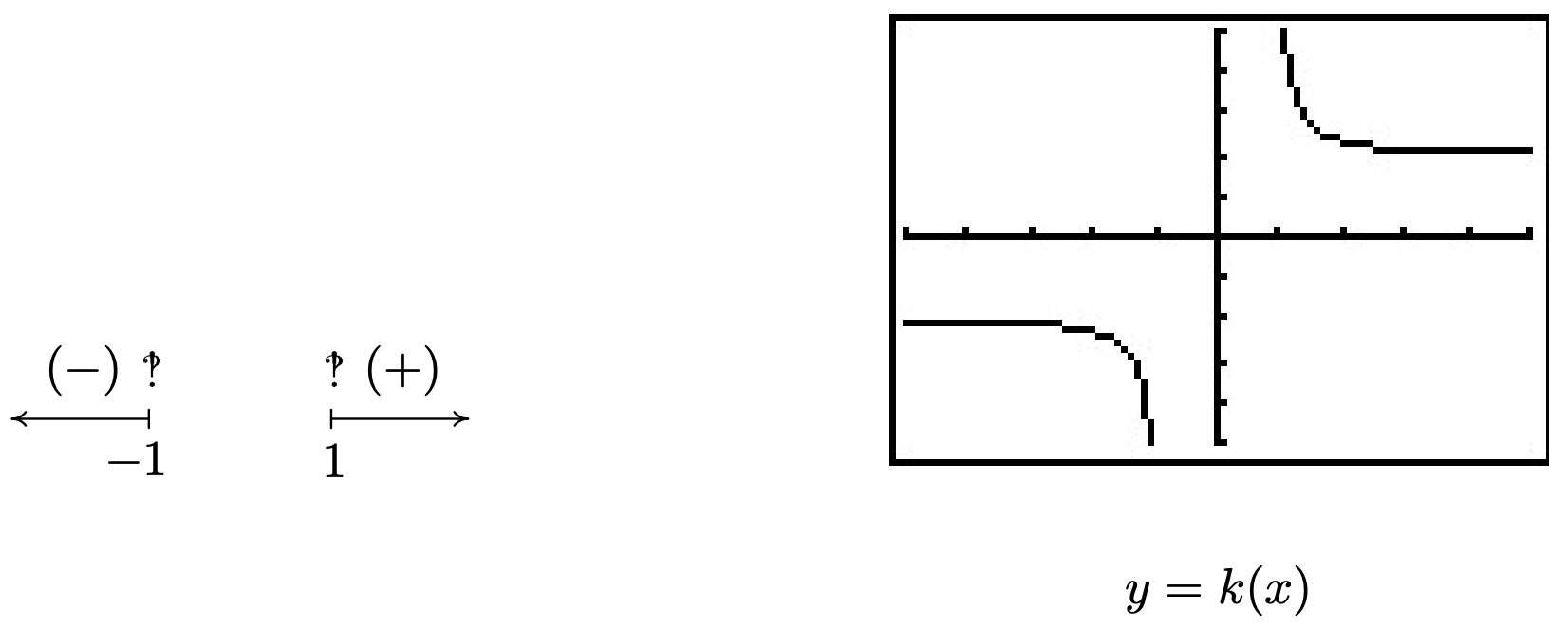
We find x2−1≥0 for (−∞,−1]∪[1,∞). To keep the denominator of k(x) away from zero, we set √x2−1=0. We leave it to the reader to verify the solutions are x=±1, both of which must be excluded from the domain. Hence, the domain of k is (−∞,−1)∪(1,∞). To build the sign diagram for k, we need the zeros of k. Setting k(x)=0 results in 2x√x2−1=0. We get 2x=0 or x=0. However, x=0 isn’t in the domain of k, which means k has no zeros. We construct our sign diagram on the domain of k below alongside the graph of k. It appears that the graph of k has two vertical asymptotes, one at x=−1 and one at x=1. The gap in the graph between the asymptotes is because of the gap in the domain of k. Concerning end behavior, there appear to be two horizontal asymptotes, y=2 and y=−2. To see why this is the case, we think of x→±∞. The radicand of the denominator x2−1≈x2, and as such, k(x)=2x√x2−1≈2x√x2=2x|x|. As x→∞, we have |x|=x so k(x)≈2xx=2. On the other hand, as x→−∞, |x|=−x, and as such k(x)≈2x−x=−2. Finally, it appears as though the graph of k passes the Horizontal Line Test which means k is one to one and k−1 exists. Computing k−1 is left as an exercise.
As the previous example illustrates, the graphs of general algebraic functions can have features we’ve seen before, like vertical and horizontal asymptotes, but they can occur in new and exciting ways. For example, k(x)=2x√x2−1 had two distinct horizontal asymptotes. You’ll recall that rational functions could have at most one horizontal asymptote. Also some new characteristics like ‘unusual steepness’8 and cusps9 can appear in the graphs of arbitrary algebraic functions. Our next example first demonstrates how we can use sign diagrams to solve nonlinear inequalities. (Don’t panic. The technique is very similar to the ones used in Chapters 2, 3 and 4.) We then check our answers graphically with a calculator and see some of the new graphical features of the functions in this extended family.
Solve the following inequalities. Check your answers graphically with a calculator.
- x2/3<x4/3−6
- 3(2−x)1/3≤x(2−x)−2/3
Solution.
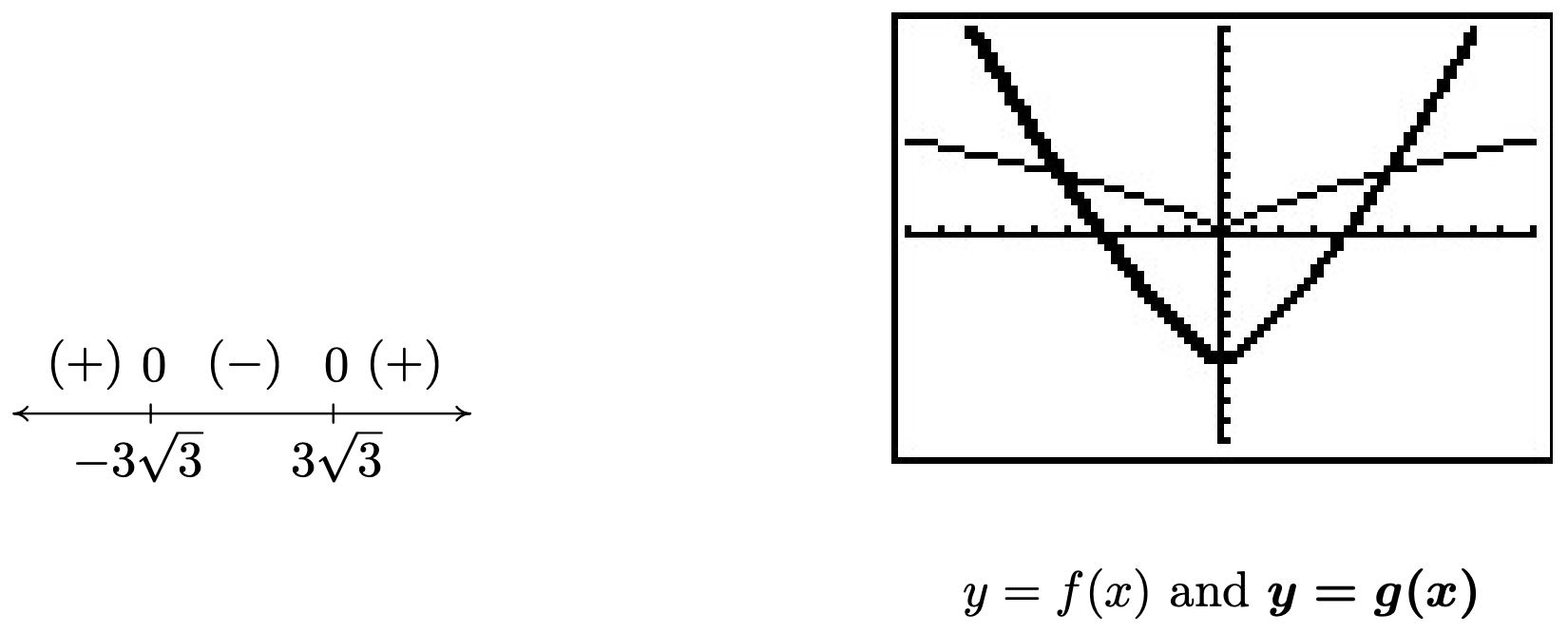
- To solve x2/3<x4/3−6, we get 0 on one side and attempt to solve x4/3−x2/3−6>0. We set r(x)=x4/3−x2/3−6 and note that since the denominators in the exponents are 3, they correspond to cube roots, which means the domain of r is (−∞,∞). To find the zeros for the sign diagram, we set r(x)=0 and attempt to solve x4/3−x2/3−6=0. At this point, it may be unclear how to proceed. We could always try as a last resort converting back to radical notation, but in this case we can take a cue from Example 3.3.4. Since there are three terms, and the exponent on one of the variable terms, x4/3, is exactly twice that of the other, x2/3, we have ourselves a ‘quadratic in disguise’ and we can rewrite x4/3−x2/3−6=0 as (x2/3)2−x2/3−6=0. If we let u=x2/3, then in terms of u, we get u2−u−6=0. Solving for u, we obtain u=−2 or u=3. Replacing x2/3 back in for u, we get x2/3=−2 or x2/3=3. To avoid the trouble we encountered in the discussion following Definition 5.5, we now convert back to radical notation. By interpreting x2/3 as 3√x2 we have 3√x2=−2 or 3√x2=3. Cubing both sides of these equations results in x2=−8, which admits no real solution, or x2=27, which gives x=±3√3. We construct a sign diagram and find x4/3−x2/3−6>0 on (−∞,−3√3)∪(3√3,∞). To check our answer graphically, we set f(x)=x2/3 and g(x)=x4/3−6. The solution to x2/3<x4/3−6 corresponds to the inequality f(x)<g(x), which means we are looking for the x values for which the graph of f is below the graph of g. Using the ‘Intersect’ command we confirm10 that the graphs cross at x=±3√3. We see that the graph of f is below the graph of g (the thicker curve) on (−∞,−3√3)∪(3√3,∞).
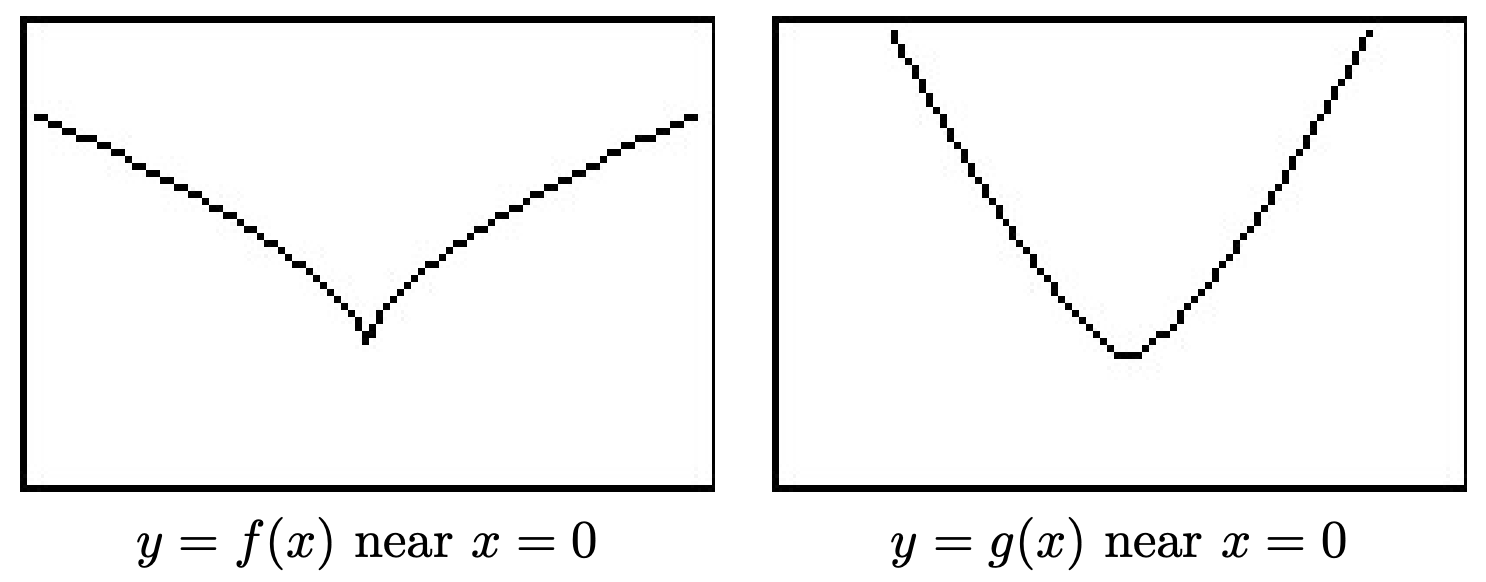
As a point of interest, if we take a closer look at the graphs of f and g near x=0 with the axes off, we see that despite the fact they both involve cube roots, they exhibit different behavior near x=0. The graph of f has a sharp turn, or cusp, while g does not.11
- To solve 3(2−x)1/3≤x(2−x)−2/3, we gather all the nonzero terms on one side and obtain 3(2−x)1/3−x(2−x)−2/3≤0. We set r(x)=3(2−x)1/3−x(2−x)−2/3. As in number 1, the denominators of the rational exponents are odd, which means there are no domain concerns there. However, the negative exponent on the second term indicates a denominator. Rewriting r(x) with positive exponents, we obtain r(x)=3(2−x)1/3−x(2−x)2/3 Setting the denominator equal to zero we get (2−x)2/3=0, or 3√(2−x)2=0. After cubing both sides, and subsequently taking square roots, we get 2−x=0, or x=2. Hence, the domain of r is (−∞,2)∪(2,∞). To find the zeros of r, we set r(x)=0. There are two school of thought on how to proceed and we demonstrate both.
- r(x)=3(2−x)1/3−x(2−x)−2/3=(2−x)−2/3[3(2−x)13−(−23)−x][6pt]=(2−x)−2/3[3(2−x)3/3−x]=(2−x)−2/3[3(2−x)1−x]since 3√u3=(3√u)3=u=(2−x)−2/3(6−4x)=(2−x)−2/3(6−4x)
To solve r(x)=0, we set (2−x)−2/3(6−4x)=0, or 6−4x(2−x)2/3=0. We have 6−4x=0 or x=32.
- Common Denominator Approach. We rewrite
r(x)=3(2−x)1/3−x(2−x)−2/3=3(2−x)1/3−x(2−x)2/3[10pt]=3(2−x)1/3(2−x)2/3(2−x)2/3−x(2−x)2/3common denominator[10pt]=3(2−x)13+23(2−x)2/3−x(2−x)2/3[10pt]=3(2−x)3/3(2−x)2/3−x(2−x)2/3[10pt]=3(2−x)1(2−x)2/3−x(2−x)2/3since 3√u3=(3√u)3=u[10pt]=3(2−x)−x(2−x)2/3[10pt]=6−4x(2−x)2/3
As before, when we set r(x)=0 we obtain x=32.
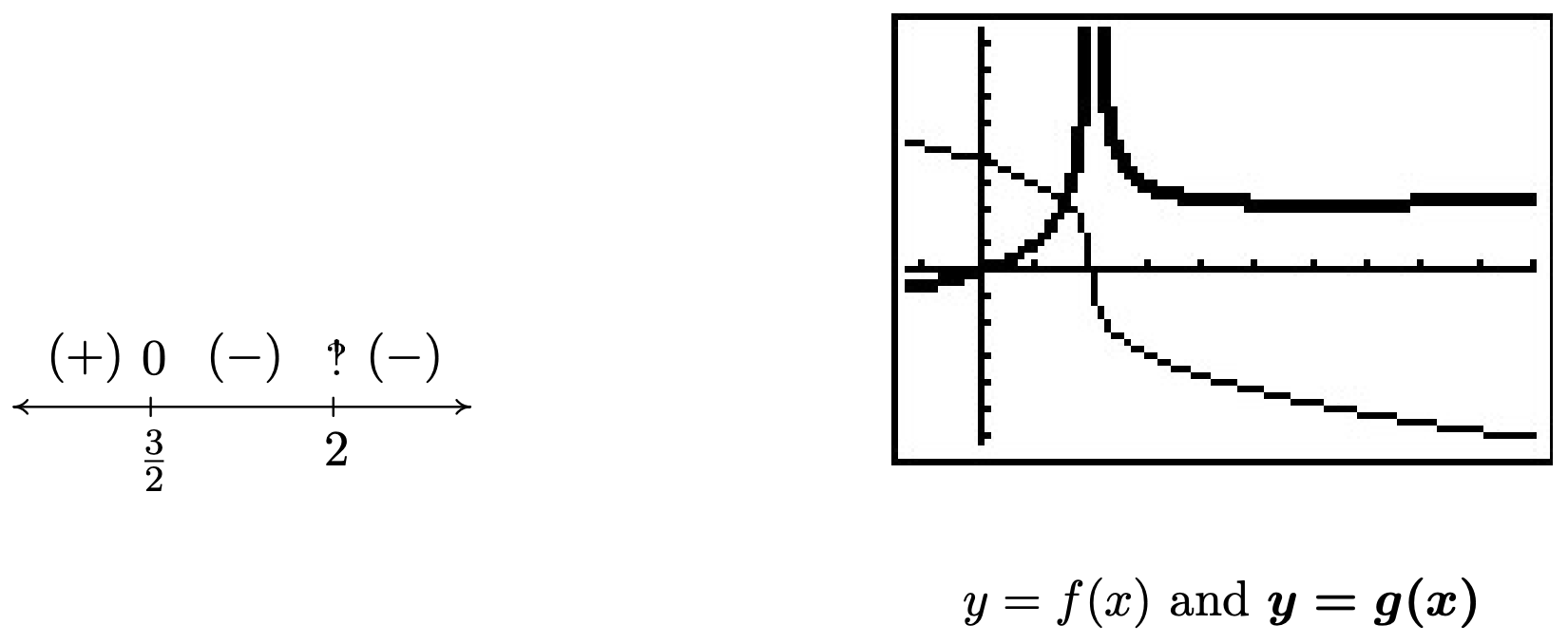
We now create our sign diagram and find 3(2−x)1/3−x(2−x)−2/3≤0 on [32,2)∪(2,∞). To check this graphically, we set f(x)=3(2−x)1/3 and g(x)=x(2−x)−2/3 (the thicker curve). We confirm that the graphs intersect at x=32 and the graph of f is below the graph of g for x≥32, with the exception of x=2 where it appears the graph of g has a vertical asymptote.
- r(x)=3(2−x)1/3−x(2−x)−2/3=(2−x)−2/3[3(2−x)13−(−23)−x][6pt]=(2−x)−2/3[3(2−x)3/3−x]=(2−x)−2/3[3(2−x)1−x]since 3√u3=(3√u)3=u=(2−x)−2/3(6−4x)=(2−x)−2/3(6−4x)
One application of algebraic functions was given in Example 1.6.6 in Section 1.1. Our last example is a more sophisticated application of distance.
Carl wishes to get high speed internet service installed in his remote Sasquatch observation post located 30 miles from Route 117. The nearest junction box is located 50 miles downroad from the post, as indicated in the diagram below. Suppose it costs $15 per mile to run cable along the road and $20 per mile to run cable off of the road.
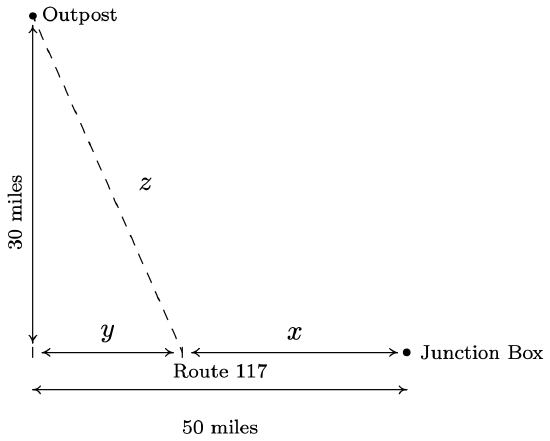
- Express the total cost C of connecting the Junction Box to the Outpost as a function of x, the number of miles the cable is run along Route 117 before heading off road directly towards the Outpost. Determine a reasonable applied domain for the problem.
- Use your calculator to graph y=C(x) on its domain. What is the minimum cost? How far along Route 117 should the cable be run before turning off of the road?
Solution.
- The cost is broken into two parts: the cost to run cable along Route 117 at $15 per mile, and the cost to run it off road at $20 per mile. Since x represents the miles of cable run along Route 117, the cost for that portion is 15x. From the diagram, we see that the number of miles the cable is run off road is z, so the cost of that portion is 20z. Hence, the total cost is C=15x+20z. Our next goal is to determine z as a function of x. The diagram suggests we can use the Pythagorean Theorem to get y2+302=z2. But we also see x+y=50 so that y=50−x. Hence, z2=(50−x)2+900. Solving for z, we obtain z=±√(50−x)2+900. Since z represents a distance, we choose z=√(50−x)2+900 so that our cost as a function of x only is given by C(x)=15x+20√(50−x)2+900 From the context of the problem, we have 0≤x≤50.
- Graphing y=C(x) on a calculator and using the ‘Minimum’ feature, we find the relative minimum (which is also the absolute minimum in this case) to two decimal places to be (15.98,1146.86). Here the x-coordinate tells us that in order to minimize cost, we should run 15.98 miles of cable along Route 117 and then turn off of the road and head towards the outpost. The y-coordinate tells us that the minimum cost, in dollars, to do so is $1146.86. The ability to stream live SasquatchCasts? Priceless.
5.3.1 Exercises
For each function in Exercises 1 - 10 below
- Find its domain.
- Create a sign diagram.
- Use your calculator to help you sketch its graph and identify any vertical or horizontal asymptotes, ‘unusual steepness’ or cusps.
- f(x)=√1−x2
- f(x)=√x2−1
- f(x)=x√1−x2
- f(x)=x√x2−1
- f(x)=4√16xx2−9
- f(x)=5x3√x3+8
- f(x)=x23(x−7)13
- f(x)=x32(x−7)13
- f(x)=√x(x+5)(x−4)
- f(x)=3√x3+3x2−6x−8
In Exercises 11 - 16, sketch the graph of y=g(x) by starting with the graph of y=f(x) and using the transformations presented in Section 1.7.
- f(x)=3√x, g(x)=3√x−1−2
- f(x)=3√x, g(x)=−23√x+1+4
- f(x)=4√x, g(x)=4√x−1−2
- f(x)=4√x, g(x)=34√x−7−1
- f(x)=5√x, g(x)=5√x+2+3
- f(x)=8√x, g(x)=8√−x−2
- x+1=√3x+7
- 2x+1=√3−3x
- x+√3x+10=−2
- 3x+√6−9x=2
- 2x−1=√x+3
- x32=8
- x23=4
- √x−2+√x−5=3
- √2x+1=3+√4−x
- 5−(4−2x)23=1
- 10−√x−2≤11
- 3√x≤x
- 2(x−2)−13−23x(x−2)−43≤0
- −43(x−2)−43+89x(x−2)−73≥0
- 2x−13(x−3)13+x23(x−3)−23≥0
- 3√x3+3x2−6x−8>x+1
- 13x34(x−3)−23+34x−14(x−3)13<0
- x−13(x−3)−23−x−43(x−3)−53(x2−3x+2)≥0
- 23(x+4)35(x−2)−13+35(x+4)−25(x−2)23≥0
- Rework Example 5.3.3 so that the outpost is 10 miles from Route 117 and the nearest junction box is 30 miles down the road for the post.
- The volume V of a right cylindrical cone depends on the radius of its base r and its height h and is given by the formula V=13πr2h. The surface area S of a right cylindrical cone also depends on r and h according to the formula S=πr√r2+h2. Suppose a cone is to have a volume of 100 cubic centimeters.
- Use the formula for volume to find the height h as a function of r.
- Use the formula for surface area and your answer to 37a to find the surface area S as a function of r.
- Use your calculator to find the values of r and h which minimize the surface area. What is the minimum surface area? Round your answers to two decimal places.
- The National Weather Service uses the following formula to calculate the wind chill: W=35.74+0.6215Ta−35.75V0.16+0.4275TaV0.16 where W is the wind chill temperature in ∘F, Ta is the air temperature in ∘F, and V is the wind speed in miles per hour. Note that W is defined only for air temperatures at or lower than 50∘F and wind speeds above 3 miles per hour.
- Suppose the air temperature is 42∘ and the wind speed is 7 miles per hour. Find the wind chill temperature. Round your answer to two decimal places.
- Suppose the air temperature is 37∘F and the wind chill temperature is 30∘F. Find the wind speed. Round your answer to two decimal places.
- As a follow-up to Exercise 38, suppose the air temperature is 28∘F.
- Use the formula from Exercise 38 to find an expression for the wind chill temperature as a function of the wind speed, W(V).
- Solve W(V)=0, round your answer to two decimal places, and interpret.
- Graph the function W using your calculator and check your answer to part 39b.
- The period of a pendulum in seconds is given by T=2π√Lg (for small displacements) where L is the length of the pendulum in meters and g=9.8 meters per second per second is the acceleration due to gravity. My Seth-Thomas antique schoolhouse clock needs T=12 second and I can adjust the length of the pendulum via a small dial on the bottom of the bob. At what length should I set the pendulum?
- The Cobb-Douglas production model states that the yearly total dollar value of the production output P in an economy is a function of labor x (the total number of hours worked in a year) and capital y (the total dollar value of all of the stuff purchased in order to make things). Specifically, P=axby1−b. By fixing P, we create what’s known as an ‘isoquant’ and we can then solve for y as a function of x. Let’s assume that the Cobb-Douglas production model for the country of Sasquatchia is P=1.23x0.4y0.6.
- Let P=300 and solve for y in terms of x. If x = 100, what is y?
- Graph the isoquant 300 = 1.23x^{0.4}y^{0.6}. What information does an ordered pair (x, y) which makes P = 300 give you? With the help of your classmates, find several different combinations of labor and capital all of which yield P = 300. Discuss any patterns you may see.
- According to Einstein’s Theory of Special Relativity, the observed mass m of an object is a function of how fast the object is traveling. Specifically, m(x) = \dfrac{m_{r}}{\sqrt{1 - \dfrac{x^{2}}{c^{2}}}}\nonumber where m(0)=m_{r} is the mass of the object at rest, x is the speed of the object and c is the speed of light.
- Find the applied domain of the function.
- Compute m(.1c), \, m(.5c), \, m(.9c) and m(.999c).
- As x \rightarrow c^{-}, what happens to m(x)?
- How slowly must the object be traveling so that the observed mass is no greater than 100 times its mass at rest?
- Find the inverse of k(x) = \dfrac{2x}{\sqrt{x^{2} - 1}}.
- Suppose Fritzy the Fox, positioned at a point (x,y) in the first quadrant, spots Chewbacca the Bunny at (0,0). Chewbacca begins to run along a fence (the positive y-axis) towards his warren. Fritzy, of course, takes chase and constantly adjusts his direction so that he is always running directly at Chewbacca. If Chewbacca’s speed is v_{1} and Fritzy’s speed is v_{2}, the path Fritzy will take to intercept Chewbacca, provided v_{2} is directly proportional to, but not equal to, v_{1} is modeled by
y = \dfrac{1}{2} \left(\dfrac{x^{1+ v_{1}/v_{2}}}{1+v_1/v_2}- \dfrac{x^{1-v_1/v_2}}{1-v_1/v_2}\right) + \dfrac{v_1 v_2}{v_2^2-v_1^2}
- Determine the path that Fritzy will take if he runs exactly twice as fast as Chewbacca; that is, v_{2} = 2v_{1}. Use your calculator to graph this path for x \geq 0. What is the significance of the y-intercept of the graph?
- Determine the path Fritzy will take if Chewbacca runs exactly twice as fast as he does; that is, v_{1} = 2v_{2}. Use your calculator to graph this path for x > 0. Describe the behavior of y as x \rightarrow 0^{+} and interpret this physically.
- With the help of your classmates, generalize parts (a) and (b) to two cases: v_{2} > v_{1} and v_{2} < v_{1}. We will discuss the case of v_{1} = v_{2} in Exercise 32 in Section 6.5.
- Verify the Quotient Rule for Radicals in Theorem 5.6.
- Show that \left(x^{\frac{3}{2}}\right)^{\frac{2}{3}} = x for all x \geq 0.
- Show that \sqrt[3]{2} is an irrational number by first showing that it is a zero of p(x) = x^{3} - 2 and then showing p has no rational zeros. (You’ll need the Rational Zeros Theorem, Theorem 3.9, in order to show this last part.)
- With the help of your classmates, generalize Exercise 47 to show that \sqrt[n]{c} is an irrational number for any natural numbers c \geq 2 and n \geq 2 provided that c \neq p^{n} for some natural number p.
5.3.2 Answers
-
f(x) = \sqrt{1 - x^2}
Domain: [-1, 1]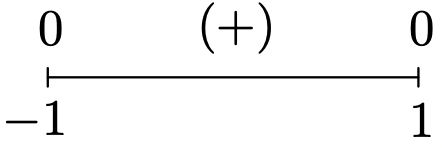
No asymptotes
Unusual steepness at x = -1 and x = 1
No cusps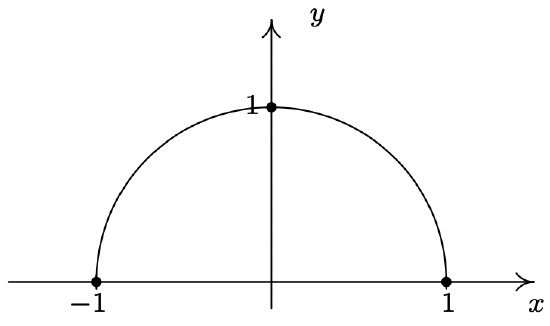
-
f(x) = \sqrt{x^2-1}
Domain: (-\infty, -1] \cup [1,\infty)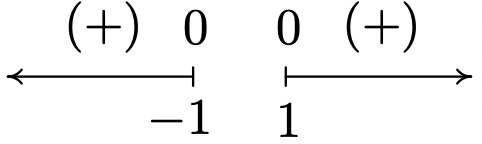
No asymptotes
Unusual steepness at x = -1 and x = 1
No cusps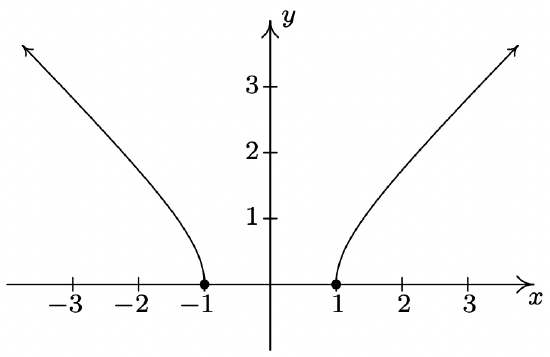
-
f(x) = x\sqrt{1-x^2}
Domain: [-1,1]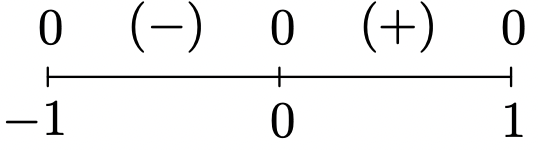
No asymptotes
Unusual steepness at x = -1 and x = 1
No cusps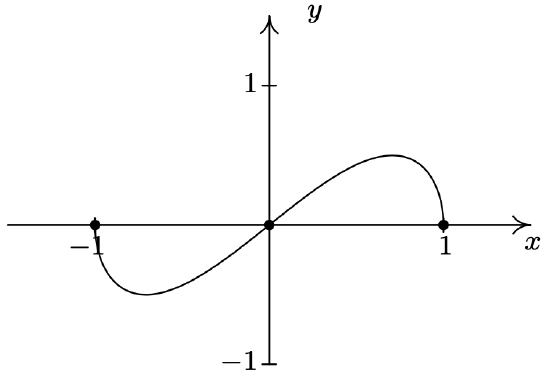
-
f(x) = x\sqrt{x^2-1}
Domain: (-\infty, -1] \cup [1,\infty)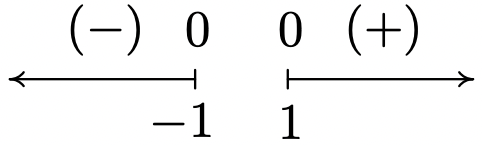
No asymptotes
Unusual steepness at x = -1 and x = 1
No cusps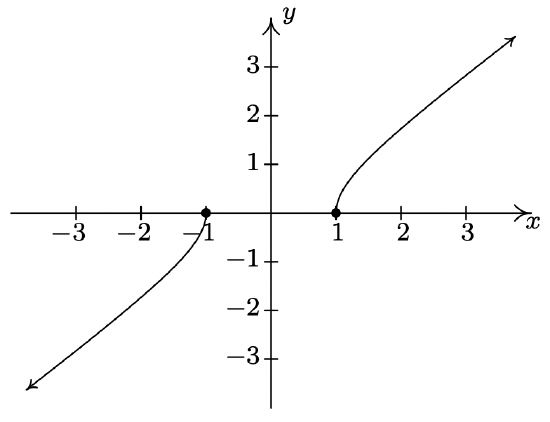
-
f(x) = \sqrt[4]{\dfrac{16x}{x^2 - 9}}
Domain: (-3, 0] \cup (3, \infty)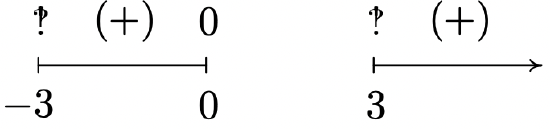
Vertical asymptotes: x = -3 and x = 3
Horizontal asymptote: y = 0
Unusual steepness at x = 0
No cusps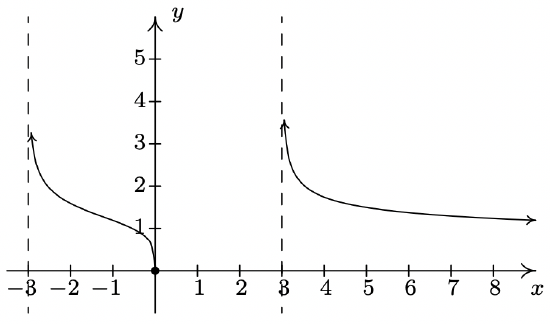
-
f(x) = \dfrac{5x}{\sqrt[3]{x^{3} + 8}}
Domain: (-\infty, -2) \cup (-2, \infty)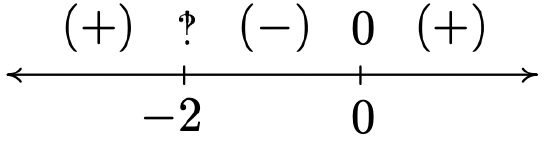
Vertical asymptote x = -2
Horizontal asymptote y = 5
No unusual steepness or cusps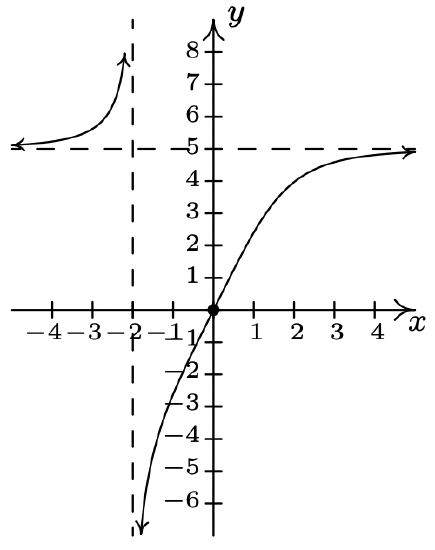
-
2 f(x) = x^{\frac{2}{3}}(x - 7)^{\frac{1}{3}}
Domain: (-\infty, \infty)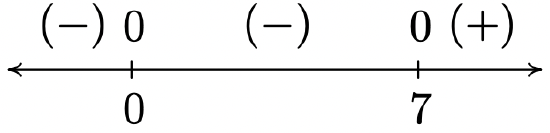
No vertical or horizontal asymptotes13
Unusual steepness at x = 7
Cusp at x = 0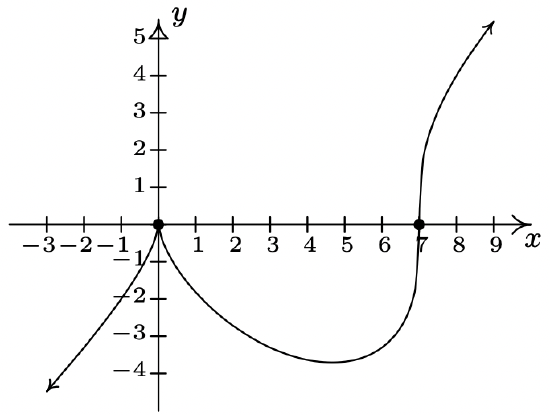
-
f(x) = x^{\frac{3}{2}}(x - 7)^{\frac{1}{3}}
Domain: [0, \infty)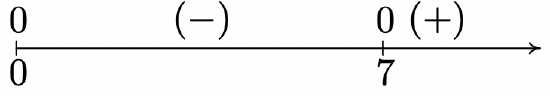
No asymptotes
Unusual steepness at x = 7
No cusps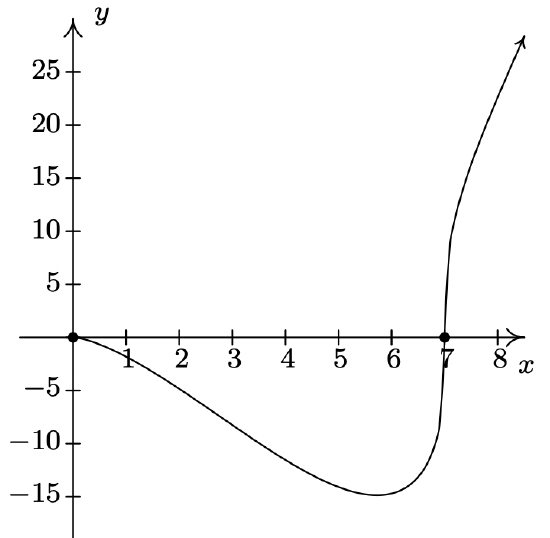
-
f(x) = \sqrt{x(x + 5)(x - 4)}
Domain: [-5, 0] \cup [4, \infty)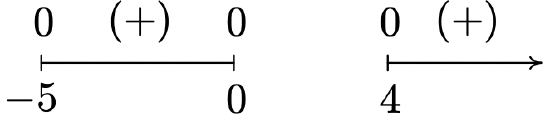
No asymptotes
Unusual steepness at x = -5, x = 0 and x = 4
No cusps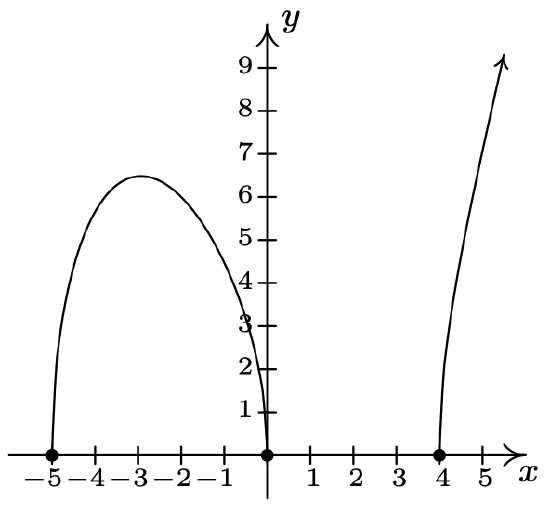
-
2 f(x) = \sqrt[3]{x^{3} + 3x^{2} - 6x - 8}
Domain: (-\infty, \infty)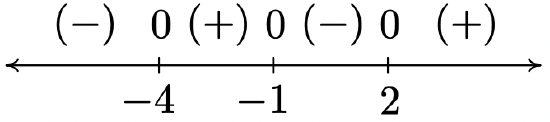
No vertical or horizontal asymptotes14
Unusual steepness at x = -4, x = -1 and x = 2
No cusps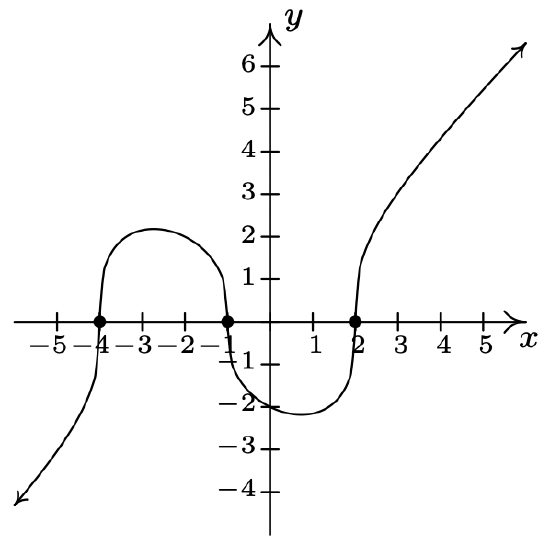
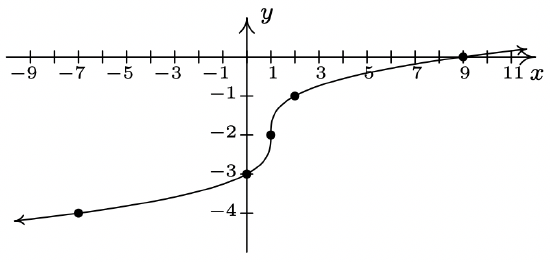
- g(x) = \sqrt[3]{x-1}-2
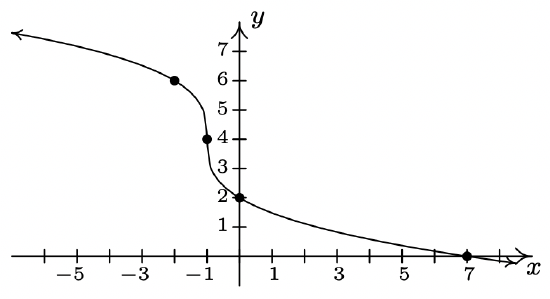
- g(x) = -2\sqrt[3]{x + 1} + 4
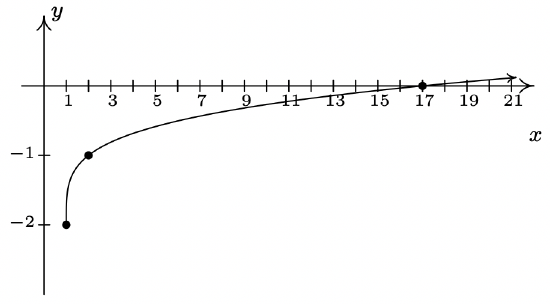
- g(x) = \sqrt[4]{x-1}-2
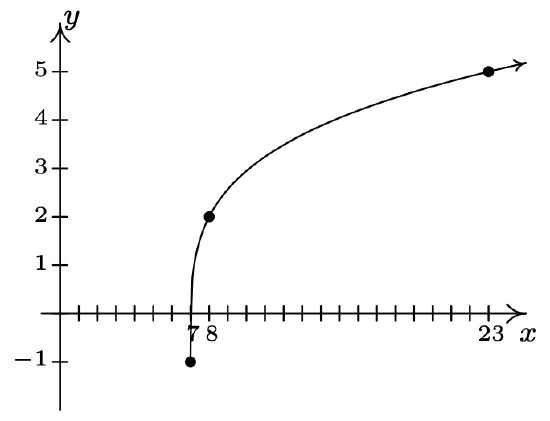
- g(x) = 3\sqrt[4]{x - 7} - 1
- g(x) = \sqrt[5]{x + 2} + 3
- g(x) = \sqrt[8]{-x} - 2
- x=3
- x = \frac{1}{4}
- x=-3
- x = -\frac{1}{3}, \; \frac{2}{3}
- x = \frac{5 + \sqrt{57}}{8}
- x = 4
- x = \pm 8
- x = 6
- x = 4
- x=-2, 6
- [2, \infty)
- [-1, 0] \cup [1, \infty)
- (-\infty, 2) \cup (2,3]
- (2,6]
- (-\infty, 0) \cup [2,3) \cup (3, \infty)
- (-\infty, -1)
- \left(0, \frac{27}{13} \right)
- (-\infty, 0) \cup (0,3)
- (-\infty, -4) \cup \left(-4, -\frac{22}{19}\right] \cup (2, \infty)
- C(x) = 15x+20\sqrt{100+(30-x)^2}, 0 \leq x \leq 30. The calculator gives the absolute minimum at \approx (18.66, 582.29). This means to minimize the cost, approximately 18.66 miles of cable should be run along Route 117 before turning off the road and heading towards the outpost. The minimum cost to run the cable is approximately \$582.29.
-
- h(r) = \frac{300}{\pi r^2}, r > 0.
- S(r) = \pi r \sqrt{r^2+\left(\frac{300}{\pi r^2}\right)^2} = \frac{\sqrt{\pi^2 r^6+90000}}{r}, r>0
- The calculator gives the absolute minimum at the point \approx (4.07, 90.23). This means the radius should be (approximately) 4.07 centimeters and the height should be 5.76 centimeters to give a minimum surface area of 90.23 square centimeters.
-
- W \approx 37.55^{\circ}F.
- V \approx 9.84 miles per hour.
-
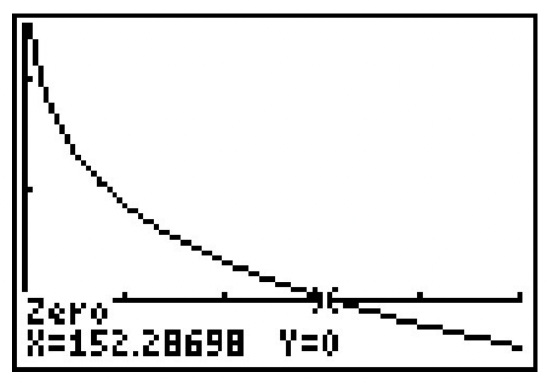
- W(V) = 53.142 - 23.78 V^{0.16}. Since we are told in Exercise 38 that wind chill is only effect for wind speeds of more than 3 miles per hour, we restrict the domain to V > 3.
- W(V)=0 when V \approx 152.29. This means, according to the model, for the wind chill temperature to be 0^{\circ}F, the wind speed needs to be 152.29 miles per hour.
- The graph is below.
- 9.8 \left(\dfrac{1}{4\pi}\right)^{2} \approx 0.062 meters or 6.2 centimeters
-
- First rewrite the model as P = 1.23x^{\frac{2}{5}}y^{\frac{3}{5}}. Then 300 = 1.23x^{\frac{2}{5}}y^{\frac{3}{5}} yields y = \left( \dfrac{300}{1.23x^{\frac{2}{5}}} \right)^{\frac{5}{3}}. If x = 100 then y \approx 441.93687.
-
- [0, c)
- \begin{aligned} &m(.1 c)=\frac{m_{r}}{\sqrt{.99}} \approx 1.005 m_{r} \quad m(.5 c)=\frac{m_{r}}{\sqrt{.75}} \approx 1.155 m_{r} \\ &m(.9 c)=\frac{m_{r}}{\sqrt{.19}} \approx 2.294 m_{r} \quad m(.999 c)=\frac{m_{r}}{\sqrt{.0 .001999}} \approx 22.366 m_{r} \end{aligned}
- As x \rightarrow c^{-}, \, m(x) \rightarrow \infty
- If the object is traveling no faster than approximately 0.99995 times the speed of light, then its observed mass will be no greater than 100m_{r}.
- k^{-1}(x) = \dfrac{x}{\sqrt{x^{2} - 4}}
-
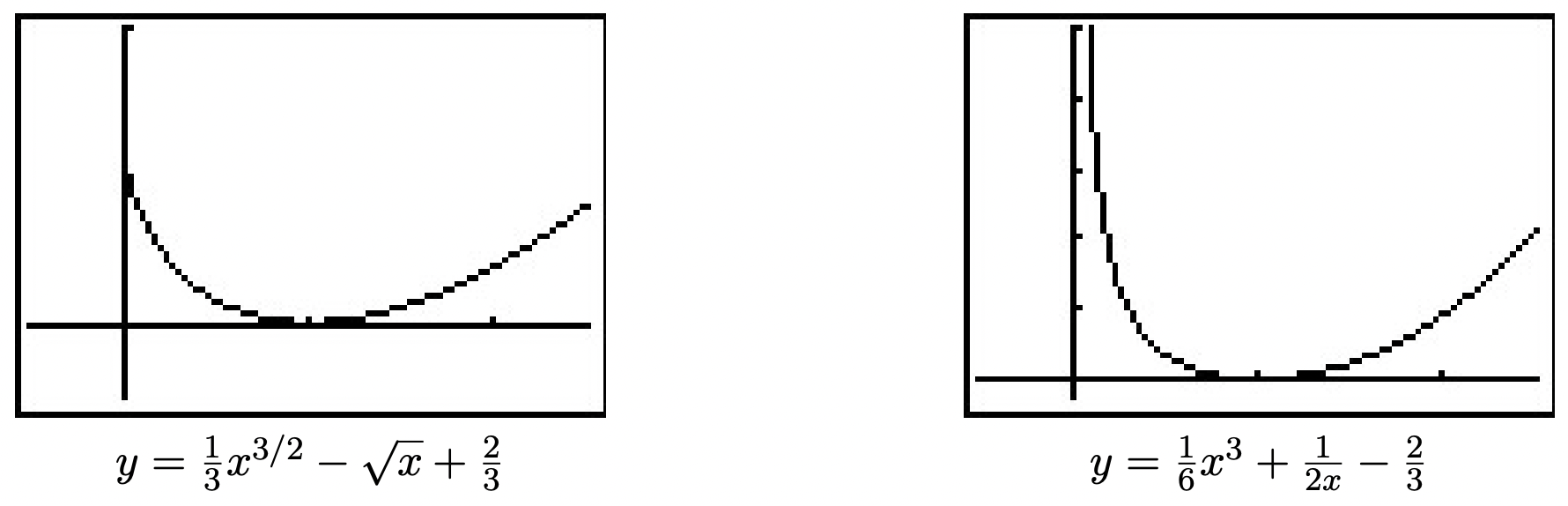
- y = \frac{1}{3}x^{3/2} - \sqrt{x} + \frac{2}{3}. The point \left(0,\frac{2}{3}\right) is when Fritzy’s path crosses Chewbacca’s path - in other words, where Fritzy catches Chewbacca.
- y = \frac{1}{6}x^3+\frac{1}{2x} - \frac{2}{3}. Using the techniques from Chapter 4, we find as x \rightarrow 0^{+}, y \rightarrow \infty which means, in this case, Fritzy’s pursuit never ends; he never catches Chewbacca. This makes sense since Chewbacca has a head start and is running faster than Fritzy.
Reference
1 Although we discussed imaginary numbers in Section 3.4, we restrict our attention to real numbers in this section. See the epilogue on page 294 for more details.
2 Otherwise we’d run into the same paradox we did in Section 3.4.
3 Did you like that pun?
4 In most other cases, though, rational exponents are preferred.
5 As mentioned in Section 2.2, f(x)=\sqrt{x^{2}}=|x| so that absolute value is also considered an algebraic function.
6 For instance, -2 \geq \sqrt[4]{x+3}, which has no solution or -2 \leq \sqrt[4]{x+3} 3 whose solution is [-3, \infty).
7 Recall, this means we have produced a candidate which doesn’t satisfy the original equation. Do you remember how raising both sides of an equation to an even power could cause this.
8 The proper Calculus term for this is ‘vertical tangent’, but for now we’ll be okay calling it ‘unusual steepness’.
9 See page 241 for the first reference to this feature.
10 Or at least confirm to several decimal places
11 Again, we introduced this feature on page 241 as a feature which makes the graph of a function 'not smooth'.
12 And we exercise special care when reducing the \frac{3}{3} power to 1.
13 Using Calculus it can be shown that y=x-\frac{7}{3} is a slant asymptote of this graph.
14 Using Calculus it can be shown that y = x + 1 is a slant asymptote of this graph.

