9.1: Trigonometric Functions of Any Angle

To define the trigonometric functions of any angle - including angles less than \(0^\circ\) or greater than \(360^\circ \) - we need a more general definition of an angle. We say that an angle is formed by rotating a ray \(\overrightarrow{OA} \) about the endpoint \(O \) (called the vertex), so that the ray is in a new position, denoted by the ray \(\overrightarrow{OB} \). The ray \(\overrightarrow{OA} \) is called the \(\textbf{initial side}\) of the angle, and \(\overrightarrow{OB} \) is the terminal side of the angle (see Figure 1.4.1(a)).

Figure 1.4.1 Definition of a general angle

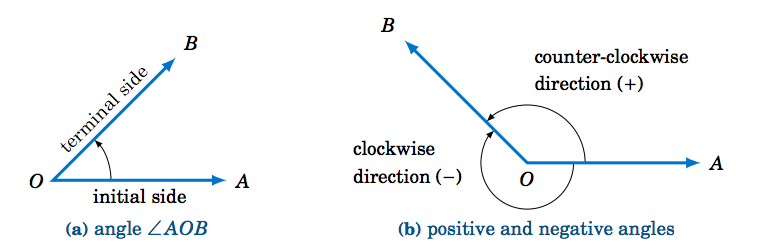
We denote the angle formed by this rotation as \(\angle\,AOB \), or simply \(\angle\,O \), or even just \(O \). If the rotation is counter-clockwise then we say that the angle is positive, and the angle is negative if the rotation is clockwise (see Figure 1.4.1(b)).

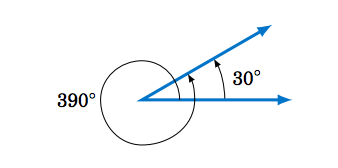
One full counter-clockwise rotation of \(\overrightarrow{OA} \) back onto itself (called a revolution), so that the terminal side coincides with the initial side, is an angle of \(360^\circ\); in the clockwise direction this would be \(-360^\circ \). Not rotating \(\overrightarrow{OA} \) constitutes an angle of \(0^\circ \). More than one full rotation creates an angle greater than \(360^\circ \). For example, notice that \(30^\circ \) and \(390^\circ \) have the same terminal side in Figure 1.4.2, since \(30 + 360 = 390 \).

Figure 1.4.2 Angle greater than \(360^◦\)

We can now define the trigonometric functions of any angle in terms of \(\textbf{Cartesian coordinates}\). Recall that the \(\mathbf{xy}\)-coordinate plane consists of points denoted by pairs \((x,y) \) of real numbers. The first number, \(x \), is the point's \(\mathbf{x} \) coordinate, and the second number, \(y \), is its \(\mathbf{y} \) coordinate. The \(x \) and \(y \) coordinates are measured by their positions along the \(\mathbf{x}\)-axis and \(\mathbf{y}\)-axis, respectively, which determine the point's position in the plane. This divides the \(xy\)-coordinate plane into four quadrants (denoted by QI, QII, QIII, QIV), based on the signs of \(x \) and \(y \) (see Figure 1.4.3(a)-(b)).

Figure 1.4.3 \(x y\)-coordinate plane

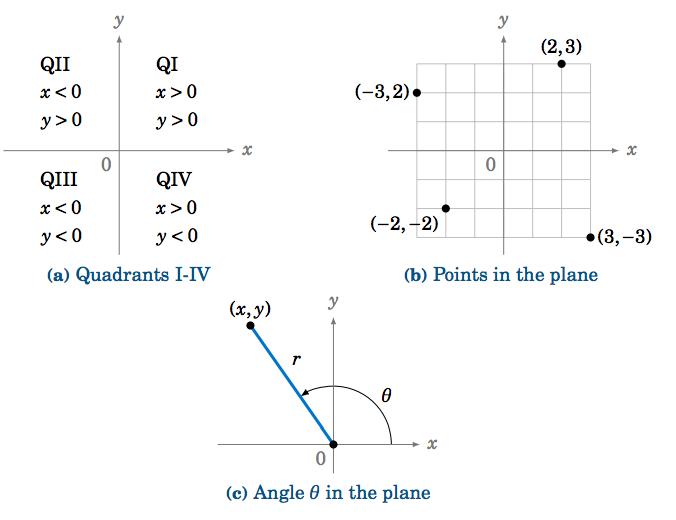
Now let \(\theta \) be any angle. We say that \(\theta \) is in standard position if its initial side is the positive \(x\)-axis and its vertex is the origin \((0,0) \). Pick any point \((x,y) \) on the terminal side of \(\theta \) a distance \(r>0 \) from the origin (see Figure 1.4.3(c)). (Note that \(r = \sqrt{ x^2 + y^2 } \). Why?) We then define the trigonometric functions of \(\theta \) as follows:

\[ \sin\;\theta ~=~ \dfrac{y}{r} \qquad\qquad
\cos\;\theta ~=~ \dfrac{x}{r} \qquad\qquad
\tan\;\theta ~=~ \dfrac{y}{x} \label{1.2}\]

As in the acute case, by the use of similar triangles these definitions are well-defined (i.e. they do not depend on which point \((x,y) \) we choose on the terminal side of \(\theta\)). Also, notice that \(| \sin\;\theta | \le 1 \) and \( | \cos\;\theta | \le 1 \), since \(| y | \le r \) and \( | x | \le r \) in the above definitions.

Notice that in the case of an acute angle these definitions are equivalent to our earlier definitions in terms of right triangles: draw a right triangle with angle \(\theta \) such that \(x = \text{adjacent side} \), \(y = \text{opposite side} \), and \(r = \text{hypotenuse} \). For example, this would give us \(\sin\;\theta = \frac{y}{r} = \frac{\text{opposite}}{\text{hypotenuse}} \) and \(\cos\;\theta = \frac{x}{r} = \frac{\text{adjacent}}{\text{hypotenuse}} \), just as before (see Figure 1.4.4(a)).

Figure 1.4.4

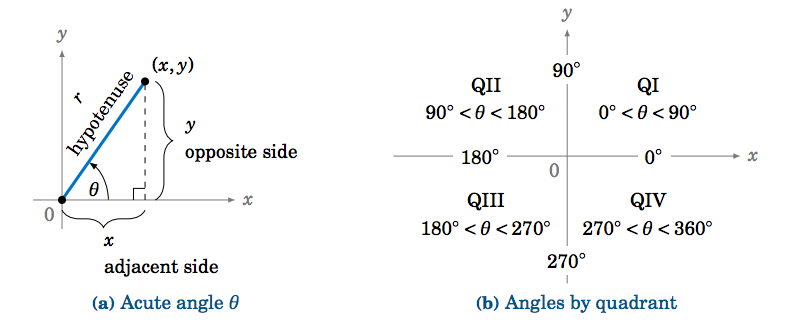
Since \(360^\circ \) represents one full revolution, the trigonometric function values repeat every \(360^\circ \). For example, \(\sin\;360^\circ = \sin\;0^\circ \), \(\cos\;390^\circ = \cos\;30^\circ \), \(\tan\;540^\circ = \tan\;180^\circ \), \(\sin\;(-45^\circ) = \sin\;315^\circ \), etc. In general, if two angles differ by an integer multiple of \(360^\circ\) then each trigonometric function will have equal values at both angles. Angles such as these, which have the same initial and terminal sides, are called coterminal.

In Examples 1.20-1.22, we saw how the values of trigonometric functions of an angle \(\theta \) larger than \(90^\circ \) were found by using a certain acute angle as part of a right triangle. That acute angle has a special name: if \(\theta \) is a nonacute angle then we say that the reference angle for \(\theta \) is the acute angle formed by the terminal side of \(\theta \) and either the positive or negative \(x\)-axis. So in Example 1.20, we see that \(60^\circ \) is the reference angle for the nonacute angle \(\theta = 120^\circ\); in Example 1.21, \(45^\circ \) is the reference angle for \(\theta = 225^\circ\); and in Example 1.22, \(30^\circ \) is the reference angle for \(\theta = 330^\circ \).

Example 1.24

Figure 1.4.7

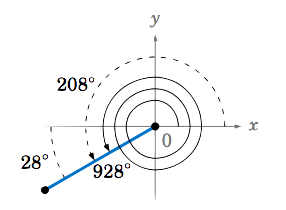
1. Which angle between \(0^\circ \) and \(360^\circ \) has the same terminal side (and hence the same trigonometric function values) as \(\theta\,\)?
2. What is the reference angle for \(\theta\,\)?

Solution

(a) Since \(928^\circ = 2 \times 360^\circ + 208^\circ \), then \(\theta \) has the same terminal side as \(208^\circ \), as in Figure 1.4.7.

(b) \(928^\circ \) and \(208^\circ \) have the same terminal side in QIII, so the reference angle for \(\theta = 928^\circ \) is \(208^\circ - 180^\circ = 28^\circ \).

Example 1.25

Suppose that \(\cos\;\theta = -\frac{4}{5} \). Find the exact values of \(\sin\;\theta \) and \(\tan\;\theta \). Also find \(\theta \) in each quadrant.

Solution

We can use a method similar to the one used to solve Example 1.8 in Section 1.2. That is, draw a right triangle and interpret \(\cos\;\theta \) as the ratio \(\frac{\text{adjacent}}{\text{hypotenuse}} \) of two of its sides. Since \(\cos\;\theta = -\frac{4}{5} \), we can use \(4 \) as the length of the adjacent side and \(5 \) as the length of the hypotenuse. By the Pythagorean Theorem, the length of the opposite side must then be \(3 \). Since \(\cos\;\theta \) is negative, we know from Figure 1.4.5 that \(\theta \) must be in either QII or QIII. Thus, we have two possibilities, as shown in Figure 1.4.8 below:

Figure 1.4.8 \(\cos θ = − \frac{4}{ 5}\)

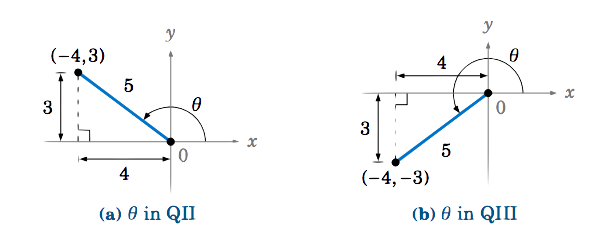
When \(\theta \) is in QII, we see from Figure 1.4.8(a) that the point \((-4,3) \) is on the terminal side of \(\theta \), and so we have \(x = -4 \), \(y = 3 \), and \(r = 5 \). Thus, \(\sin\;\theta = \frac{y}{r} = \frac{3}{5} \) and \(\tan\;\theta = \frac{y}{x} = \frac{3}{-4} \).

When \(\theta \) is in QIII, we see from Figure 1.4.8(b) that the point \((-4,-3) \) is on the terminal side of \(\theta \), and so we have \(x = -4 \), \(y = -3 \), and \(r = 5 \). Thus, \(\sin\;\theta = \frac{y}{r} = \frac{-3}{5} \) and \(\tan\;\theta = \frac{y}{x} = \frac{-3}{-4} =
\frac{3}{4} \).

Thus, either \(\fbox{\(\sin\;\theta = \frac{3}{5} \) and \(\tan\;\theta = -\frac{3}{4}\)}\) or \(\fbox{\(\sin\;\theta = -\frac{3}{5} \) and \(\tan\;\theta = \frac{3}{4}\)}\).

If \(\cos\;\theta = -\frac{4}{5} \) were solved we would get \(\theta \) = 143.14, which lies in quadrant II. The reference angle is 36.87. To determine the angle in quadrant III, \(\theta \) = 180 + 36.87 = 216.87.

For an angle \(θ\) in standard position and a point \((x, y)\) on its terminal side:

1. \(\sin\;\theta \) has the same sign as \(y\)
2. \(\cos\;\theta \) has the same sign as \(x\)
3. \(\tan\;\theta \) is positive when \(x \) and \(y \) have the same sign
4. \(\tan\;\theta \) is negative when \(x \) and \(y \) have opposite signs

Contributors

• Michael Corral (Schoolcraft College). The content of this page is distributed under the terms of the GNU Free Documentation License, Version 1.2.